Формирование тонких оболочек из пыли Леметра - Толмена - Бонди

Решение Леметра - Толмена - Бонди (ЛТБ), описывающее поведение неоднородного сферического пылевого облака, в последнее время получило широкое применение в космологии. Одна из причин этого в том, что решение ЛТБ является наиболее простым из известных решений, которые могут описывать влияние пространственной неоднородности постоянной Хаббла и плотности вещества на красное смещение света, приходящего к наблюдателю от прошлых событий. В то же время, решение ЛТБ в общем случае содержит две произвольные функции, что позволяет при соответствующем их выборе объяснить известную зависимость яркости удаленных сверхновых от красного смещения без привлечения темной энергии. Подробное изложение идеи и обзор работ в данной области можно найти в [1, 2]. Другой важной особенностью решения ЛТБ является возможность описания войдов - пустых или сильно разреженных областей пространства, окруженных стенками с много большей концентрацией галактик. По современным данным войды являются неотъемлемой частью крупномасштабной структуры Вселенной (см. пример моделирования и краткий исторический обзор в [3]).

Один из способов моделирования стенки, окружающей войд - использование бесконечно тонкой оболочки, описываемой формализмом сшивки Дармуа - Лихнеровича - Израэля [4-6]. Такие модели давно применяется для построения неоднородных космологических моделей [7], объяснения зависимости между фотометрическим расстоянием и красным смещением [8,10], а также для описания аномалий анизотропии реликтового излучения [9,11]. Однако в природе не существует бесконечно тонких объектов, поэтому в нашей работе рассматриваются способы предельного перехода к оболочкам от более реалистичных моделей, описываемых решением ЛТБ.

1.    Решение Леметра — Толмена — Бонди

В сопутствующей системе отсчета метрику ЛТБ можно записать в виде

Г2(т R)

ds2 = dT2   ---- 二 dR2 - г2(т, R)(dӨ2 + sin2 Өdф2).

1 + E(R)''

Каждый слой пыли имеет свое фиксированное значение радиальной координаты R. Функция г(т, R) определяет расстояние до ттеитра для частпті пыли с данным R ii является решением уравнений

Г2 = E(R) + ^mR,(L2)

r

• ¹    E-mail: drivvl@mail.ru

• ²    E-mail: tegai_s_f@inbox.ru

  
  
  
2.    Сферический пылевой слой в пустоте

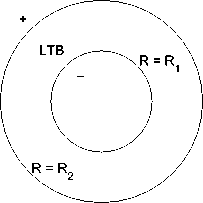
Рис. 1. Схематическое изображение модели. 'LTB' - пространство Леметра - Толмена - Бонди, 」- пространство Минковского, — - внешнее пространство Шварцшильда или Фридмана.

―mrR) ，                         ( L3)

где¹ (функция m(R) им ( ? ( ?т смысл суммарной массы слоев веп 【 ества с радиальными координатами м ( ?иышпш R. Плотность пыли да ( ?тся выражением

Р^{(т, R}) = 4   mH 2 .                        (LI)

4пг2(т, R—т, R )

Рассмотрим сферический слой пыли, окружающий пустое пространство. На внешней границе соединим этот слой, описываемый решением ЛТБ, с внешним пространством Шварцшильда или Фридмана (рис. 1). Подобные модели рассматривались в ряде работ [9,12,13], однако нашей целью будет изучение предельного перехода к бесконечно тонкой промежуточной области. Устремим толщину слоя пыли к нулю, оставляя его массу неизменной. Получится ли в результате такого перехода бесконечно тонкая оболочка, описываемая формализмом Израэля?

В формализме Израэля тонкая оболочка, разделяющая некоторые внутреннее и внешнее подпространства, описывается процедурой сшивки, условия которой заключаются в совпадении метрик, индуцированных на оболочке с внешней (+) и внутренней (-) сторон:

do±2 = dT2 — д±Ө("Ө2 + sin2 Өdф2).                               (2.1)

Внутреннее время оболочки т выбрано так, чтобы коэффициент при dT2 равнялся единице:

g±T = 1.                                                 ( 2-2)

Условия сшивки (2.2) вместе с g+ө = g— должны удовлетворяться после выполнения предельного перехода к тонкой оболочке от рассматриваемой трехслойной модели.

Теперь выполним сшивку промежуточного слоя неоднородной пыли с окружающими его областями. В отличие от модели тонкой оболочки здесь сшивка производится по геометрическим поверхностям, не имеющим внутренней массы. Из-за того, что мы выбрали сопутствующую систему отсчета, уравнение внутренней и внешней поверхностей задаются простыми соотношениями R = Ri .R = R2 соответственна где¹ Ri, R2 — константы. К условшо совпадения первых (фундаментальных форм добавляется требование равенства внешних кривизн поверхности сшивки, вычисленных с разных её сторон. Так как все присутствующие в модели решения имеют нулевое давление, это требование приводит к непрерывности текущей массы Мизнера - Шарпа. То есть m(Ri) = 0- m(R2 ) = M. 「 ne M — полная масса промежуточного слоя.

Метрика, индуцированная на поверхностях сшивки решением ЛТБ имеет вид do2,2 = dT2 — г2(т, Ri,2)(d。2 + sin2 Өdф2).

(2.3)

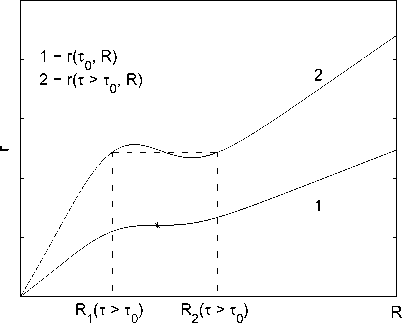
Рис. 2. Радиальная метрическая функция г(т, R) после образования каустики (расширяющийся интервал [Rl ( T ) ,R 2 ( t )] выфезаетсн п заменягтся т<>нкоіі оболочкой}.

Каждая из угловых компонент г2(т, Ri,2)по условиям сшивки совпадает с соответствующей ком-поис'итоп д±Ө- Но в пределе нулевой толшпиы g+^ = ggg- следовательно lim г(т, Ri) = r(T,R2).                                    (2」)

R it R‘ 2

А так как мы работаем в сопутствующей системе отсчета, то и все производные по времени от (функции г(т, R) при Ri т R2 должны стать непрерывными. Таким образом левая часть уравнения (1.3) должна быть непрерывна в пределе тонкой оболочки. Но правая часть этого же уравнения должна иметь скачок, так как содержит массу в числителе. Отсюда можно сделать вывод, что бесконечно тонкий слой пыли Леметра - Толмана - Бонди не дает тонкой оболочки в смысле формализма сшивки Израэля.

• 3.    Тонкая оболочка как слабое решение

для пространства Леметра — Толмена — Бонди

Для моделирования формирования тонкой оболочки возьмем начальные условия, приводящие, начиная с некоторого момента времени т°, к пересечению различных слоев пыли (каустике). В классическом решении наличие каустики приводит к тому, что производная r' ( T,R) в некоторой области становится меньше нуля, что соответствует нефизической ситуации из-за отрицательной плотности (1.4). Кроме того, в результате пересечения слоев одному и тому же распределению материи внутри сферы площади 4пг2(т, R) сответствуют разлившые значения массы m(R) [14]. Чтобы избавиться от отрицательной плотности, вырежем сферический слой от R = Ri (т) до R = R ? ( t ) (рис. 2), содержащий нежелательные эффекты. Оставшиеся части соединим, следуя формализму Дармуа — Лихиеровича — Израеля. Так как значения массы m(Ri), m(R?) на границах вырезанной области различны, сшивка должна быть выполнена на тонкой оболочке ненулевой массы, а не на геометрической поверхности.

Поведение тонкой оболочки находится из условий сшивки. В качестве внутренних координат оболочки £“ выберем время т ii углы Ө, ф. Тогда, метрика на поверхности оболочки примет вид d負,2 =(1 - 1 +E1 2 (ri,2 dRT2) ) dT2 - r2,2 (d。2 + sin2 Өdф2) ,             (3-1)

где¹ индексы 1,2 указыватот на значения (функций на внутренней R = Ri (т) п внешиеп R = R ? ( t ) поверхностях оболочки соответственно. Из непрерывности первой фундаментальной формы следует

占(ri需)2 = А 4)2,          -

Г1 = Г2 = Г.

(3.3)

Первое уравнение имеет два решения. Для того, чтобы получить требуемый скачок массы, выберем решение с противоположными знаками:

ri     dRi        r2     dR2

“ + Ei dT    “ + E2 dT

(3.4)

Выбор одинаковых знаков дает классическое пространство-время ЛТБ.

Дифференцирование второго условия сшивки (3.3) вместе с (3.4) позволяет найти производные dR1,2/dτ

dRi,2 _ r2,1 --1,2

， 1 + Ei,2

dT       ri, 2     ,1 + Ei + ,1 + E2

(3.5)

и затем скорость рассматриваемой тонкой оболочки

dr — r + r ， dRi,2 — Г і , 1 + Ei + 户 2,1 + E2 dT ， i* dT      ,1 + Ei + ,1 + E2

(3.6)

Для E = 0 < ) TO выражение в точности совпадает со скоростью ударной волны, полученной в [15] из условий Ренкина - Гюгонио.

Тензор энергии-импульса полученной модели имеет вид

T ^ав = Tавл ь + SabeO^b) 坛( X ) .

(3.7)

Здсч?ь 5s(X)— дельта (функция Дирака с носителем на тонкой оболочке. Т^пь импульса пыли. Sab имеет смысл поверхностного тензора энергии-импульса и связан с внешней кривизной оболочки Kab уравнением Лаицоша

µ

^Sab = — 賞(及 bl-".

(3.8)

До пересечения слоев пыли все компоненты Sj равны нулю и пространство-время описывается решением ЛТБ. После возникновения каустики диагональные компоненты Sj могут быть интерпретированы как поверхностная плотность а и тангенциальное давление р, и принимают вид

σ≡

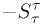
△ m

2nr² J ( ,1 + 瓦 + УГ+ E2 ) 2 - ( 「 2 - Г і ) ²

(3.9)

p 三 $^Ө = Mm⁵ 卜⁽ r^{2 - Г і ) 2 ( Р 2 - Р і )} r^{2 -} й - rf) ⁽ r^{2 - Г і )} △ m ， ] ，       ( 3.1° )

где¹ △ m = m2 - mi — масса оболочки.

Численный расчет конкретной модели войда с образованием тонкой оболочки вокруг него был выполнен в [16]. По построению нашей модели масса оболочки ms = m(R?) — m(Ri) не может оставаться постоянной. Она растет (рис. 3) за счет поглощения вещества из внутренней и внешней областей. В то же время из закона сохранения S'^ = 0 следует [17,18]

4nr2

I а + 2 r (а + р) r

)

ms + 8 пг 「 р = 0.

(3.11)

То есть, тангенциальное давление образовавшейся оболочки не может быть равно нулю, несмотря на то, что исходное вещество является пылью.

Заключение

Мы рассмотрели два возможных способа формирования движущейся тонкой оболочки в модели разреженной вакуоли, помещенной в расширяющуюся Вселенную. Для первого из них получен отрицательный результат - невозможно произвести предельный переход от сферического слоя пыли Леметра - Толмена - Бонди конечной толщины к бесконечно тонкой оболочке той же массы.

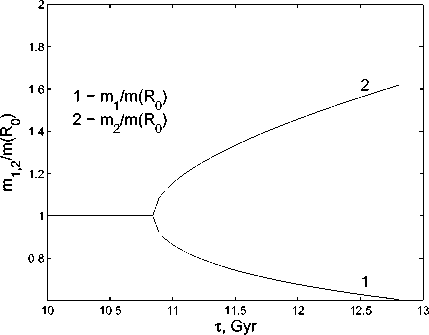
Рис. 3. Масса Мизнера - Шарпа с внутренней и внешней сторон оболочки.

Второй способ, описывает тонкую оболочку, возникающую как слабое решение уравнений Эйнштейна после пересечения различных слоев пыли. Так как эта модель является неоднородной, то в ней работает общий механизм объяснения наблюдаемого ускоренного расширения Вселенной без привлечения темной энергии. Недостатком модели является наличие поверхностного давления на оболочке, означающего негравитационное взаимодействие вещества, составляющего оболочку. Наличие взаимодействия затрудняет космологическую интерпретацию модели как стенки, состоящей из галактик и их скоплений и окружающей относительно пустую область пространства.

Возникающие трудности на наш взгляд связаны с условиями применимости уравнения состояния пыли в целом и решения Леметра - Толмена - Бонди в частности. Традиционное ограничение состоит в том, что при возрастании плотности вещества в нем возникают взаимодействия, приводящие к ненулевому давлению. Однако для космологических моделей это не вполне верно, так как даже при гипотетическом прохождении одной стенки галактик через другую, основным остается гравитационное взаимодействие. В космологических моделях с каустиками нарушение применимости решения Леметра - Толмена - Бонди возникает другим способом. Оно связано с тем, что тензор энергии-импульса пыли является результатом некоторого молчаливого усреднения дискретного распределения частиц пыли. При этом гравитационное поле находится из неусредненных уравнений Эйнштейна. Процедура усреднения в общей теории относительности из-за нелинейности уравнений чрезвычайно сложна и до сих пор является открытой проблемой, однако еще в [19] было показано, что в общем случае в результате усреднения в уравнениях Эйнштейна возникают дополнительные слагаемые, связанные с корреляциями гравитационных полей отдельных частиц. Такие слагаемые должны быть учтены при дальнейшем аналитическом моделировании формирования тонких оболочек в общей теории относительности.