Формирование внутреннего приближенного зацепления цилиндроконических передач
Автор: Лопатин Борис Александрович, Полуэктов Евгений Анатольевич, Хаустов Сергей Андреевич
Рубрика: Технология
Статья в выпуске: 11 (228), 2011 года.
Бесплатный доступ
При формировании рабочих профилей зубьев шестерни цилиндро-конической передачи внутреннего зацепления возникает технологическая проблема получения теоретически точного профиля зубьев. Это связано с необходимостью изготовления для каждой передачи долбяка с внутренними зубьями с геометрией, идентичной геометрии колеса передачи. В работе описан способ формирования приближенного профиля зубьев шестерни цилиндро-конической передачи инструментом реечного типа. Предлагаемый способ обеспечивает достаточную для практического применения степень приближения формируемой поверхности к теоретически точной.
Шестерня, зубчатое колесо, цилиндро-коническая передача, внутреннее зацепление, формообразование зубьев
Короткий адрес: https://sciup.org/147151513
IDR: 147151513 | УДК: 621.833
Текст научной статьи Формирование внутреннего приближенного зацепления цилиндроконических передач
Цилиндро-конической называется зубчатая передача, в которой одно из колес по форме заготовки является цилиндрическим, а другое коническим [1]. В статье рассматривается передача с конической шестерней и цилиндрическим колесом внутреннего зацепления, изготавливаемым зубодолблением по обычной технологии. Для обеспечения линейного контакта зубьев в цилиндро-конической передаче внутреннего зацепления, согласно второму способу Оливье, производящим колесом в станочном зацеплении должно быть эвольвентное прямозубое цилиндрическое колесо, идентичное цилиндрическому колесу передачи.
Схема внутреннего цилиндро-конического зацепления с эвольвентным цилиндрическим производящим колесом показана на рис. 1. Присвоим параметрам наклонной (конической) шестерни индекс 1, а параметрам производящего колеса - индекс 2. В схеме использованы следующие правые прямоугольные системы координат: Si и S2 - подвижные, связанные с шестерней и производящим колесом; S' и S - неподвижные. Положение подвижных систем координат колес Si и S2 относительно их неподвижных систем координат S' и S в произвольный момент времени определяется углами ф1 и ф2. Система S относится к исходному звену передачи, ее осям индексы не присваиваются.
Начала координат О всех систем совмещены с точкой пересечения осей зубчатых колес, оси аппликат систем Si и S' (^ и W') - с осью шестерни, а систем S2 и S (W2 и W) - с осью производящего колеса; оси ординат подвижных систем Si и S2 (У] и У2) - лежат в плоскостях симметрии зуба шестерни и впадины зубьев колеса соответственно. Все системы координат правые.
Мгновенная ось относительного движения колес 1 и 2 является одновременно осью зацепления L (см. рис. 1), через которую проходят нормали во всех точках мгновенного контакта сопряженных поверхностей зубьев.
Боковая поверхность зубьев колеса передачи (она же производящая поверхность) представляет собой эвольвентный цилиндр. Эта поверхность (см. рис. 1) в подвижной системе координат X2y2W2, связанной с колесом, описывается уравнениями:
^2~гЬ2^п^Уу2 Wm) Vy2"cos(Vy2 VwXk У2 = r62[cos(vy2 - v62) + vy2 -sin(vy2 -уЬ2)] i W2=u,
где rb2 - радиус основного цилиндра колеса, vy2 - угол развернутости эвольвенты, \|/62 - половина угловой толщины впадины зуба на основной окружности колеса, и - аппликата торцового сечения колеса.
Угол vy2 при заданном радиусе гу2 определяется по выражению vy2 =tgarccos(-^-). (2)
ry2
Угол Vm находится по зависимости л 2-x2-tga .
^Ь2 = ---- +--- + mv а, (3)
2-z2 z2
где х2 - коэффициент смещения колеса.
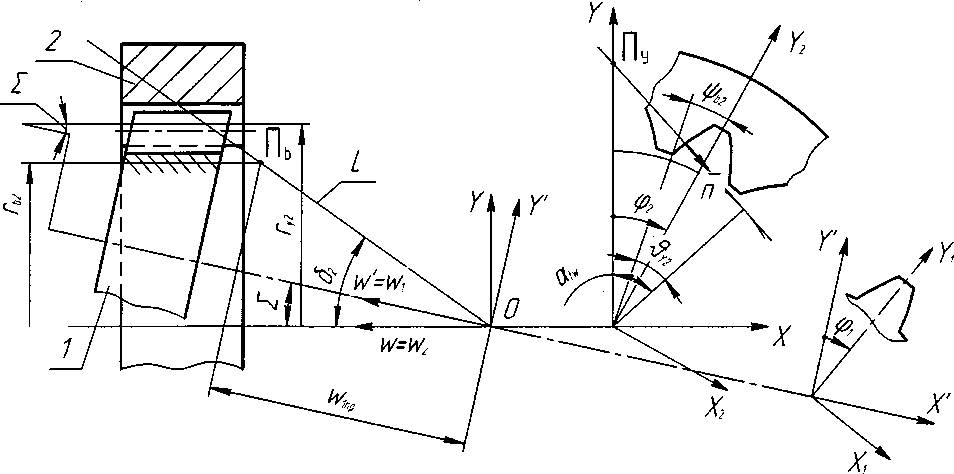
Рис. 1. Станочное зацепление производящего колеса (2) и конической шестерни (1)
Боковая поверхность зубьев шестерни является огибающей производящей поверхности и будет неэвольвентной [2]. Эта поверхность в подвижной системе координат XiKiWi, связанной с шестерней, описывается уравнениями:
%i =/^[cosq^Csina^ -v^cosa^-sinq^cosSXcosa^ + vy2 sina^^ + Msinq^sinS;
Kt = r62[sinq)1(sinah1, -Vy2cosahv)-cosq)1cos2(cosanv + vy2 sin a^J-n cosq)j sin£;
W, = rb2 sin^cosa^ + vy2sinanv) + ncosZ ; (4)
cos a^ = cos (v 2 - уи + q>,) = —;
Mtgd2
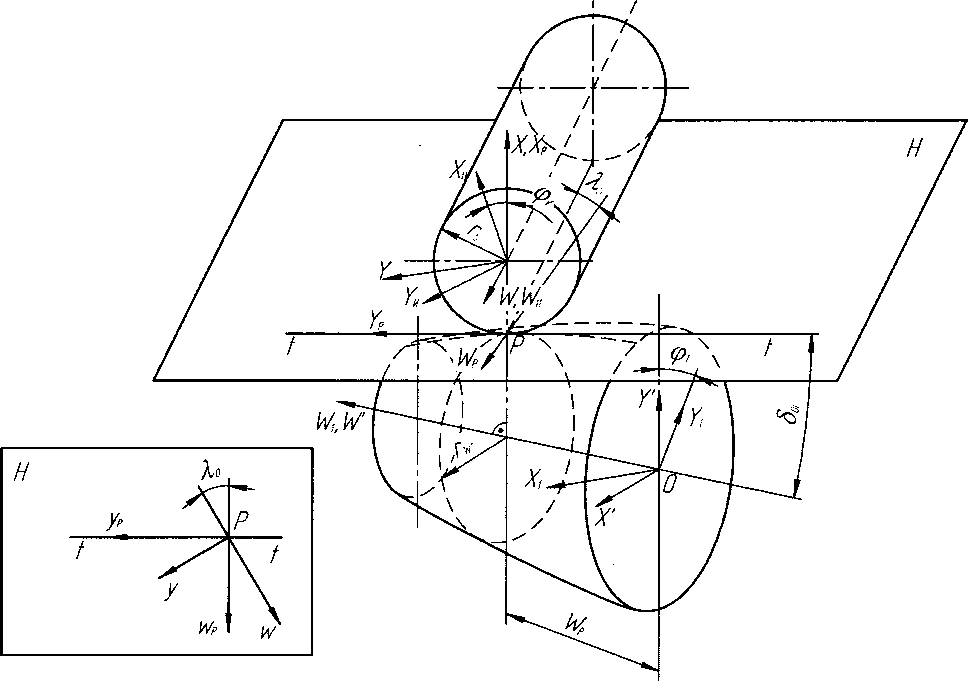
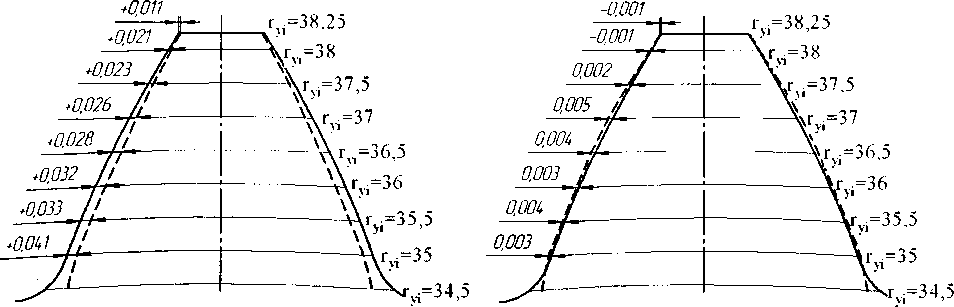
Ф1 = Ф2 h2 ’ где 2 - межосевой угол, aIW - угол зацепления в торцовом сечении колеса, Теоретически точная боковая поверхность зубьев шестерни может быть образована долбя-ком с внутренними зубьями. При этом в станочном зацеплении будет реализована геометрокинематическая схема внутреннего сопряженного цилиндро-конического зацепления. Однако ввиду сложности изготовления долбяков с внутренними зубьями такой инструмент промышленностью не выпускается. Кроме того, даже в случае создания долбяка с внутренними зубьями, осуществление способа зубодолбления неэвольвентных конических колес требует специальной оснастки станка, включающей шарнир равных угловых скоростей для связи вертикальной оси стола с осью заготовки, наклоненной под углом Е к вертикали. При этом геометрия инструмента должна быть идентична геометрии производящего колеса. Таким образом, практическое формирование теоретически точного профиля указанным способом в настоящее время невозможно. Приближенный профиль может быть получен на зуборезном оборудовании режущим инструментом реечного типа [3]. При этом способе инструмент реечного типа (фреза, шлифовальный круг) перемещается вдоль оси заготовки по определенному закону. Такое нарезание осуществляется на типовых зубофрезерных станках, имеющих следящее копирное устройство (как и при нарезании бочкообразных зубьев колес) или на станках с ЧПУ. Схема нарезания показана на рис. 2. Подбирая траекторию движения инструмента, можно получить зуб, близкий по форме точному неэвольвентному зубу колеса. Для расчета координат точек огибающей кривой воспользуемся математическим аппаратом эвольвентно-конического зацепления, разработанным В.И. Безруковым [4], принимая при расчетах угол наклона инструмента 80, переменным в каждом сечении. Коэффициент смещения инструмента в произвольном торцовом сечении шестерни в середине высоты зуба определяют из выражения , ТЕ . . ч Z xti = (— ----mv а„ + inv сс .)------ 2rcpi 2z " ^2tga(, где sti - толщина зуба в середине высоты теоретически точного профиля; а,? - торцовый угол на радиусе rcpi; z - число зубьев нарезаемой шестерни; rcpi - радиус шестерни, соответствующий середине высоты зуба. Таким образом, нарезаемую шестерню можно представить как состоящую в осевом направлении из элементарных эвольвентно-конических колес одинакового торцового модуля т, но с разным торцовым углом зацепления an и радиусом основной окружности rbi, которые определяются из следующих выражений: tg ati = tg a • cos 50/, гы = r•cos aZi . (6) Определив значение коэффициента смещения xti для разных торцовых сечений венца шестерни, путем аппроксимации получим уравнение следующего вида: xti aw2 +bw+c, (7) где a, b, с - коэффициенты, которые получены при аппроксимации; w - аппликата торцового сечения шестерни. Умножая это уравнение на модуль, получим уравнение огибающей делительной поверхности инструмента y = xti-m = (aw2 + bw + с)т. Текущее значение угла 80, между касательной к кривой, описываемой уравнением (8), и осью у (см. рис. 2) определяется по формуле 80, = -arctg(2aw, + b). Траектория движения оси фрезы - эквидистанта г огибающей делительной поверхности инструмента. Расстояние между этими кривыми равно делительному радиусу фрезы г0. По рис. 2 определим текущие координаты точек О, траектории оси фрезы: yOi = aw2 + Zw + c + r0cos80/;(10) w0/=w + r0sin80/,(11) причем ордината yOi равна текущему межосевому расстоянию ayi в станочном зацеплении. Тогда окончательно получим y0i=ayi=a'w2+b'wi+c'.(12) Коэффициенты этого уравнения находятся аналогично коэффициентам выражения (8). В предложенном способе нарезаемая поверхность зубьев шестерни получается приближенной к теоретически точной неэвольвентной поверхности описываемой уравнением (4). Для оценки отклонений нарезанного профиля от теоретически точного необходимо иметь математическое описание рабочей поверхности зубьев шестерни в процессе двухпараметрического огибания ее инструментом реечного типа, движущегося по криволинейной траектории. При выводе уравнения боковой поверхности зубьев неэвольвентной шестерни, использовался математический аппарат, разработанный Н.П. Крыловым и М.Л. Ериховым для случая двухпараметрического огибания [5]. Для получения уравнения исследуемой поверхности уравнение поверхности витков фрезы перепишем в систему, связанную с заготовкой, и полученные зависимости дополним двумя уравнениями зацепления. Параметры, используемые в расчетных зависимостях, имеют следующие обозначения (индекс 0 относится к инструменту, индекс 1 - нарезаемому колесу): т - нормальный модуль (стандартный); zo - число заходов фрезы; Ху и Х60 - углы подъема винтовой линии на делительном и основном цилиндрах; а и а( - углы профиля инструмента в нормальном и торцовых сечениях (а = 20°); р - винтовой параметр; г0 и г№ - радиусы делительного и основного цилиндров; v и и - криволинейные координаты (параметры) эвольвентной винтовой поверхности; сро (ф1) и wp - параметры огибания (угол поворота фрезы или заготовки и аппликата точки фрезы). Как было показано выше, в станочном зацеплении точка оси фрезы движется по криволинейной траектории, описываемой квадратным трехчленом (12). При этом огибающая делительной поверхности фрезы представляет собой эквидистантную к траектории оси фрезы кривую. Поверхность, образованную вращением этой кривой вокруг оси заготовки, и делительный цилиндр фрезы примем в качестве начальных поверхностей в станочном зацеплении. Взаимное расположение начальных поверхностей и применяемые системы координат показаны на рис. 3. Начальные поверхности касаются друг друга в точке Р. Общая касательная плоскость Н к ним в точке Р наклонена к оси заготовки под переменным углом 80|. Прямая t-t, касательная к образующей начальной поверхности заготовки в точке Р, лежит в плоскости Н и составляет с образующей начального цилиндра фрезы угол 90°+Ау. На рис. 3 введены следующие основные системы координат: подвижные Su и 5Ь жестко связанные соответственно с инструментом и заготовкой; неподвижная система S связана с фрезой. Вспомогательные системы Sp и S' связаны соответственно с плоскостью Н и заготовкой. Системы Su и Si ориентированы так, что отрицательная полуось Хи в сечении Yu = 0 является осью симметрии впадины фрезы, а плоскость KiWi - плоскостью симметрии зуба заготовки. Все системы координат правые. Аппликата wp точки Р в системе Si принята в качестве второго независимого параметра огибания. Радиус начальной окружности заготовки rwl в точке Р и угол 80, являются функциями параметра wp и находятся по выражениям (8; 9) при замене в них w на wp. Для преобразования систем координат в рассматриваемом станочном зацеплении воспользуемся матричным методом. Переход от системы Su к Si описывается матричным равенством П = MwM0-pMp0M0u7u =МХиги, (13) где М10.; М0,р; Мр0; МОи - матрицы перехода в соответствующих системах координат. При двухпараметрическом огибании уравнения зацепления в неподвижной системе S имеют вид ^^(^о; V№Wp)e№=0, (14) -(01 ф) —(01 Wp) где V и V - векторы скорости относительного движения соответственно при wp = const и ф = const, 7(0) - орт нормали к поверхности витка фрезы. Рис. 3. Схема станочного зацепления при нарезании неэвольвентной шестерни После рассмотрения уравнений связи параметров при wp = const, ф = const и выполнения соответствующих преобразований уравнения зацеплений приведем к следующему виду: при wp = const tg а^ = (v -1,5 л + inv а,) sin2 А60 + + r6O[(zoi +sinA0cos501)0,5sin2X60 +cos2XfcO(sin0sin5O! -cosX0 cos0cos5O()] + + (r0cos50z + rwl)(O,5sinXocos0sin2Xo -cosX0 cos2X60) r№ (cos 0 sin X№ + cos Xo sin 0 cos 50,) ’ при ф = const sin 0[ tg а^ (tg Xo tg Х60 + cos а,) - (v -1,5 л + inv а,) tg Ло tg Лй0 ] + „ COS0 + COSCL r (1 + tg 5O.)/2 _ , „ +cos 0 cos a, +------------ [r0---— ---] +1 = 0. гьо ^a Для того чтобы получить уравнение поверхности, необходимо выполнить перемножение матриц равенства (13). После преобразований получим: х, = Г cos ф, + у' sin ф[; у, =-х'8тф, +у'со8ф1; (17) ^ = (х + r0) sin 50/ + g cos 50/ + wp, где x^ysin^o + ^cosX^; у' = (х + r0)cos50|. - gsin50, + rwX; g = уcosX0 - wM sinA0; x = rг,0[cos(v + фи) + tga(ysin(v + фu)]; (18) у = r60[sin (v + ф„) - tga^ cos(v + Ф„)]; % = гьо tg ho (v -1,5я + inv a, - tg a,y); 5to = -arctg(2awp + b) ; rwl = aw2 + bwp+c. Выражения (17), (18) совместно с (15) и (16) представляют собой уравнения боковой поверхности зуба шестерни, нарезанной червячной фрезой. Полученные уравнения позволяют произвести оценку отклонения нарезаемой поверхности инструментом реечного типа и теоретически точного профиля следующим способом. Определяем абсциссу хХТ и ординату ухт точки теоретической поверхности (4), имеющей аппликату wln и расположенной на окружности радиуса гуХ. Находим координаты xln, yln, wln точки поверхности зуба неэвольвентной шестерни по уравнению (17) и радиус этой точки ryl = \^х^^х^- Оценку отклонения поверхностей производим по разности толщин зубьев, измеренных по дуге окружности радиуса гуХ, которые рассчитываем по полученным значениям координат хХп, уХп и ххт, ухт. Сравнительный анализ профилей показал, что максимальные отклонения возникают в ряде передач в крайних торцовых сечениях шестерни и составляют сотые доли миллиметра. При этих отклонениях на больших торцах получаемый профиль зуба больше теоретического, что может нарушить работу передачи из-за возникновения интерференции или кромочного контакта в зацеплении. Устранение отклонений профиля можно осуществить назначением модификации зубьев шестерни при ее нарезании [6]. Сущность модификации заключается в корректировке коэффициентов смещения исходного контура инструмента, по которым рассчитывалась траектория фрезы в тех торцовых сечениях шестерни, где наблюдаются максимальные отклонения профиля. Величина модификации для каждой передачи назначается индивидуально. На рис. 4 представлены в качестве примера отклонения профиля в крайнем торцовом сечении шестерни цилиндро-конической передачи до и после модификации (см. рис. 4, а, б). Параметры рассматриваемой передачи: модуль передачи m = 2 мм, число зубьев шестерни гх = 34, число зубьев колеса гг = 40, коэффициент смещения колеса х2 = 2,21, межосевой угол передачи L = 9°; эксцентриситет водила е = 6,3 мм. Из сравнения этих профилей видно, что назначение модификации позволяет исключить возможность кромочного контакта и интерференции зубьев в передаче. Способ нарезания зубьев конических колес был использован при проектировании и изготовлении планетарных редукторов с цилиндро-коническими зацеплениями на предприятии ФГУП «Государственный научно-производственный ракетно-космический центр «ЦСКБ-Прогресс» [7]. В качестве примера на рис. 5 представлена одна из конструкций редуктора. Такие редукторы обладают рядом положительных характеристик, в частности, их нагрузочная способность сопоставима с нагрузочной способностью волновых передач, а ресурс работы в несколько раз выше. Кроме того, они обладают свойством самоторможения, что исключает применение дополнительных тормозящих устройств и позволяют осуществлять выборку зазоров в зубчатых зацеплениях. Перечисленные достоинства планетарных редукторов с цилиндро-коническими зацеплениями предопределили их применение в электромеханических приводах повышенного ресурса космических аппаратов нового поколения. - теоретический профиль зуба шестерни - нарезаемый профиль зуба шестерни а) Рис. 4. Отклонения профиля конической шестерни: а - до модернизации; б - после модернизации Рис. 5. Планетарный редуктор с внутренними цилиндро-коническими зацеплениями: а - конструкция редуктора: 1 - входной вал; 2 - неподвижное эвольвентное колесо; 3 - конические шестерни; 4 - выходной вал (эвольвентное колесо); б - детали редуктора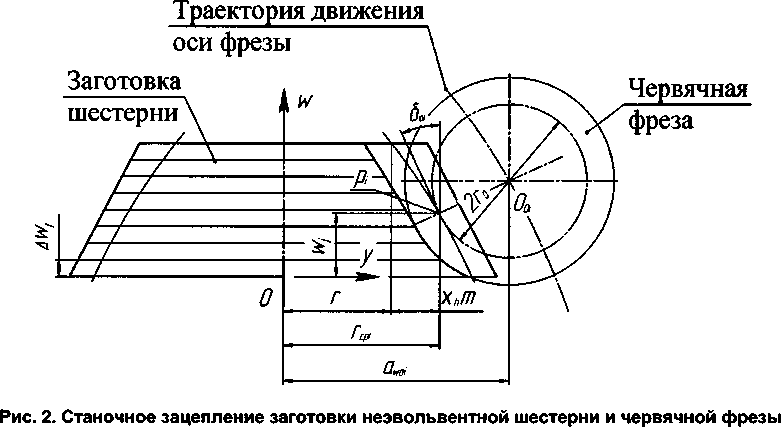

Список литературы Формирование внутреннего приближенного зацепления цилиндроконических передач
- Давыдов, Я.С. Неэволъвентное зацепление/Я.С. Давыдов. -М.: Машгиз, 1950. -180 с.
- Зайнетдинов, Р.И. Исследование и разработка эксцентриковой планетарной передачи с наклонными сателлитами: дис.... канд. техн. наук/Р.И. Зайнетдинов. -Челябинск, 1985. -232 с.
- Пат. 2364480 С1 Российская Федерация, МПК В 23 5/24. Способ нарезания зубьев неэвольвентной шестерни цилиндро-конической передачи внутреннего зацепления/Б.А. Лопатин, Е.А. Полуэктов, ДБ. Лопатин и др. -№ 2008117944; заявл. 04.05.2008; опубл. 20.08.2009, Бюл. №23.-2 с.
- Безруков, В.И. Зубчатые передачи с эволъвентно-коническими колесами/В.И. Безруков//Справочник по геометрическому расчету эволъвентных зубчатых и червячных передач/И.А. Болотовский, В.И. Безруков, О.Ф. Васильева, Б.И. Гурьев. -2-е изд., испр. и доп. -М.: Машиностроение, 1986. -С. 254-261.
- Литвин, Ф.Л. Теория зубчатых зацеплений/Ф.Л. Литвин. -М.: Наука, 1968. -584 с.
- Плотникова, С.В. Обеспечение требуемой точности профиля неэвольвентной шестерни продольной модификацией зубьев/С.В. Плотникова, Е.А. Полуэктов//Наука ЮУрГУ. Секция технических наук. -Челябинск: Издательский центр ЮУрГУ, 2009. -Т. 1. -С. 292-294.
- Свидетельство о государственной регистрации программы для ЭВМ 200961002. Программный комплекс расчета и анализа геометрии зацеплений цилиндро-конических зубчатых передач/Б.А. Лопатин, C.A. Хаустое, Е.А. Полуэктов и др. -№ 2009614819; заявл. 04.09.2009; зарегистрировано 29.10.2009.


