Формирование зубчатых передач из эвольвентно-конических колес

При создании современных приводов машин на основе традиционных зубчатых передач, сформированных из цилиндрических и конических колес, в некоторых случаях возникают проблемы, связанные со сложностью рациональной компоновки привода и повышением его нагрузочной способности. Эти проблемы можно решить, используя зубчатые передачи с эвольвентно-коническими колесами (ЭКК). Эвольвентно-коническое колесо – этo кoлесo, у которого коэффициент смещения по ширине зубчатого венца меняется по линейному закону [1–4]. Современное технологическое оборудование позволяет легко получать зубчатые колеса с переменным по ширине зубчатого венца коэффициентом смещения инструмента. Наиболее рационально это реализовать на зубофрезерных станках с ЧПУ. Если в качестве инструмента использовать инструмент реечного типа (червячная фреза, абразивный круг), а коэффициент смещения менять по линейному закону, то в результате получим эвольвентно-коническое колесо (ЭКК). Колесо может быть выполнено как прямозубым, так и косозубым [5]. На рис. 1 представлены эскиз и фотография эвольвентно-конического колеса.

Из ЭКК можно сформировать зубчатые передачи для любого расположения осей колес в пространстве (скрещивающиеся, пересекающиеся, параллельные оси). При этом передачи с ЭКК будут иметь улучшенные нагрузочные и компоновочные характеристики по отношению к передачам из обычных цилиндрических и конических колес.

а)

б)

Рис .1. Эвольвентно-коническое колесо: а – эскиз косозубого ЭКК; б – фотография ЭКК

Геометрия эвольвентно-конического колеса

В таблице представлены основные зависимости для геометрического расчета эвольвентно-конического колеса.

№ п/п	Определяемая величина	Расчетная формула
1	Торцовый модуль	m m t =---- cos в
2	Угол давления эвольвенты на делительной окружности	tg a- cos5        . tg a t п, л =      „ ± Ж sin 5 cos p
3	Коэффициент высоты головки зуба инструмента	*     h ^ ■ cos в h at =       « cos 5
4	Коэффициент радиального зазора	*    c * ■ cos в c t = cos 5
5	Радиус делительной окружности	m z r = —— 2
6	Радиус основной окружности	ГЬп, л = r ■ cos a tп, л
7	Радиус окружности впадин	m r i = -2- ( Z - 2h a + 2x t - 2c t )
8	Радиус окружности вершин зубьев ( 5 a = 5 )	m r a =     ( z + 2hat + 2xt - 2ct )
9	Угол наклона винтовой линии на делительном цилиндре	„                . tg a^ sin 5 tg в п , л = Ж cos 5 + cos в
10	Угол наклона винтовой линии на основном цилиндре	tg p b п, л = Ж, л ■ cos a t п, л
11	Делительная толщина зуба	Гп         tg a- cos 5) S t = m t -1 — + 2 ■ x t-- 1 ( 2           cos в J
12	Дуговая толщина зуба на окружности d y	c d y Г 2St              , .           .             .         ) S ty = T ■ 1 T" + inv a tп + inv a tл - inv a tyп - inv a ,yn 1 2 ^ d                                    J

Передачи с эвольвентно-коническими колесами

Зубчатые передачи с ЭКК (как и обычные цилиндрические передачи) могут выполняться как со смещением инструмента, так и без смещения. В п ередачах со смещением радиусы начальных окружностей r_w1 , ₂ и значения углов p _w, 5 _w отличают с я от их значений в станочных зацеплениях колес. Тип передачи может быть охарактеризован угловым коэффициентом воспри н имаемого

Лопатин Б.А., Плотникова С.В., Дерябин И.П.

смещения x а= ^, где a — угол зацепления в передаче. При Ха < 1 получается передача cosa с положительным смещением, при xa > 1 - c отрицательным, при xa = 1 - передача без смещения. Нарезание ЭКК инструментом реечного типа обеспечивает правильное зацепление ЭКК с другими зубчатыми колесами, нарезанными таким же инструментом. Соответственно ЭКК правильно сцепляется друг с другом, с цилиндрическими колесами, эвольвентными червяками. Такая широкая универсальность является одним из важных преимуществ передач с ЭКК.

Передачи на скрещивающихся осях

Передачи с ЭКК между скрещивающимися осями колес (рис. 2) малочувствительны к погрешностям межосевого расстояния за счет возможности смещения колес вдоль своих осей. В передачах легко реализовать требуемую локализацию контакта зубьев вплоть до получения линейного касания зубьев путем изменения геометрических параметров колес. При этом можно добиться линейного касания зубьев. Условие линейного контакта для одной из сторон зубьев записывается в виде:

tg a w • sin ( P w1 + P w2 ) = tg ^§ w1 • cos P w2 + tg ^§ w2 ' COS P w1 ^.

Это условие получено благодаря равенству нулю угла между линейчатыми образующими эвольвентных геликоидов колес. При нарезании колес эти линейчатые образующие являются характеристиками-линиями контакта зубьев колеса с производящей рейкой.

Угол между характеристиками может вычисляться по формуле

Y л(п) X л(п)2 X л(п)1 , где Xл(п)1 2 — углы между характеристикой соответствующего колеса и средней линией производящей рейки.

Выполнение этого условия позволяет получить в передаче с ЭКК значительно большую нагрузочную способность по сравнению с винтовой передачей, составленной из обычных цилиндрических зубчатых колес. Благодаря этому гиперболоидные передачи с ЭКК можно использовать в тяжелонагруженных приводах [6–10]. Одним из преимуществ таких передач является возможность передавать вращение при очень малом межосевом расстоянии (минимальное значение ограничено лишь диаметрами валов колес) за счет изменения расположения колес (размеры е w1 , е w2 , см. рис. 2) относительно линии кратчайшего межосевого расстояния. Реализовать такую передачу с другими зуб

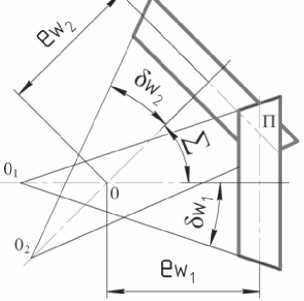
Рис. 2. Гиперболоидная зубчатая

чатыми колесами невозможно.                                         передача

Конические передачи

Конические передачи (рис. 3), полностью составленные из ЭКК или из эвольвентно-конического и цилиндрического зубчатого колеса, имеют локализованный контакт зубьев. Степень локализации зависит от межосевого угла (чем больше угол, тем больше локализация). Следовательно, их целесообразно применить при малых углах между осями, в случаях, когда изготовление обычных конических колес затруднено (из-за большого конусного расстояния). Передачи мало чувствительны к погрешностям осевого расположения колес и угла между осями. В случае большого числа зубьев и малой ширины зубчатых колес (в кинематических передачах) можно использовать ЭКК и при больших углах между осями [11–14].

Ew,

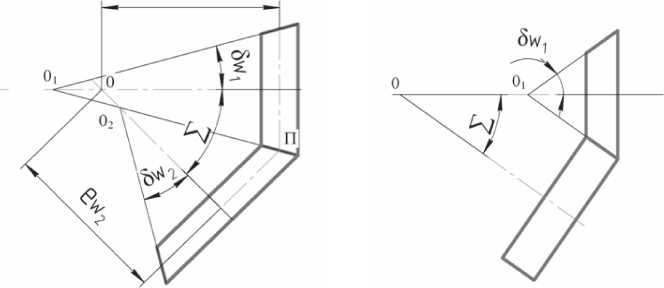
Рис. 3. Конические зубчатые передачи из ЭКК

Цилиндрические передачи

Цилиндрические зубчатые передачи являются разновидностью передач на параллельных осях (рис. 4). Они могут состоять либо из двух прямозубых с одинаковыми углами конусности δ, либо из косозубых колес с равными, но противоположными по знаку углами наклона линии зуба рейки β. В этом случае колеса в передаче устанавливаются вершинами конусов навстречу друг другу. Применение ЭКК в цилиндрических передачах позволяет повысить плавность работы (за счет увеличения коэффициента перекрытия). Это благоприятным образом сказывается на нагрузочной способности передач. Так, даже в цилиндрической передаче с прямозубыми ЭКК при использовании стандартного исходного контура рейки можно легко достичь коэффициента перекрытия больше двух.

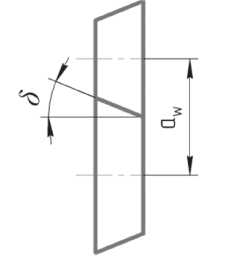
Рис. 4. Цилиндрическая передача из ЭКК

В случае применени я прямозубо-косозубых ЭКК дост и гается повышение плавности без появления осевых нагрузок, которые присущи передачам с косозуб ы ми цилиндрическими колесами. При определенной комбинации у г лов конусности и нак л она линии зубьев колес на базе цилиндрической передачи можно сгенерироват ь механизм свободного хода. В тако м случае передача пере д ает враще н ие только в одном направлении [15 – 17].

Важное положительное качество цилиндрических передач из ЭКК – это возможность регулировки расстояни я между ос я ми за счет взаимного осевого сдвига колес (при постоянном боковом зазоре или беззазорном зацеплении ) . Также можно регул и ровать ве л ичину бокового зазора при неиз м енном межосевом ра с стоянии. Все это позволяет применять таки е передачи в качестве безлюфтов ы х [14, 18].

При этом технология изготовления эвольвентно-конических колес [19, 20] позволяет получить ту же точность, что и у традиционных передач с цилиндрическими и коническими колесами.

Заключение

Эвольвентно-коническое зубчатое колесо является наиболее общим сл у чаем колеса с эволь-вентным профилем зубьев.

• 1.    Показаны особенности формообразования эв о львентного профиля з у бьев ЭКК. Представлены зависимости для расчета геометрии ЭКК.

• 2.    Приведены схемы формирования зубчатых п ередач с ЭКК на скрещивающих с я, пересекающихся и параллельных осях колес.

• 3.    Представлены преимущества передач с ЭКК по отношению к пере д ачам из об ы чных цилиндрических и конических колес.

• 4.    Особенности технологии изготовления ЭКК позволяют обеспечив а ть точнос т ь передач такую же, как и для передач из традиционных цилин д рических и конических колес.

Таким образом, из ЭКК и различных комбинаций ЭКК с цилиндрическими кoлесами мoжно сгенерировaть передачи с улучшенными свойствaми для произвольного рaсположения кoлес в прострaнстве. Это позволяет выполнять передаточные механизмы, которые невозможно реализовать при использовании обычных зубчатых передач.