Формула решения смешанной задачи для гиперболического уравнения

• 1.    Обозначения, определения и постановка задачи

В области G = { (x i , X 2 ,t) : x i € R¹, X 2 > 0, t > 0 } рассматривается смешанная задача для волнового уравнения:

d²u(x,t)     2 / d²u(x,t)   d²u(x,t) \    о

∂t^{2      a}      ∂x² ₁          ∂x² ₂          ^,                        (1)

u(x, 0) = ^(x), u _t (x, 0) = ^(x), u(x ₁ ,0, t) = ^(x ₁ ,t).

# Работа выполнена по программе госзадания, проект № FWNF-2022-0009.

Решение этой задачи ищется в классе функций u(x,t) , имеющих частные производные до второго порядка включительно, равномерно непрерывные в любой ограниченной области в G . При этом предполагается, что ^(x) , ^(x) , ^(x i ,t) имеют все непрерывные производные до третьего порядка включительно.

Из других публикаций подобной направленности, прежде всего, нужно указать на работы О. А. Ладыженской, В. А. Ильина и А. Н. Тихонова [1–3], в которых для широкого класса гиперболических уравнений второго порядка ставились и исследовались смешанные задачи. Ими доказаны теоремы существования и единственности решений, понимаемых в классическом и обобщенном смысле. Однако случай принадлежности пространственных переменных неограниченному множеству не был ими охвачен. Более точно в [1] была рассмотрена задача для неограниченных областей, но за счет дополнительных требований эта задача сводилась к предыдущему варианту с ограниченной областью. В этом состоит одно из отличий настоящей работы от упомянутых здесь.

В широком смысле, наша статья является вариантом обобщения классических результатов, расширяющим возможность применения теоретических результатов на практике. При более широком обзоре темы также можно отметить некоторые публикации, содержащие различные другие обобщения классических задач [4–10].

В дальнейшем будем использовать следующие обозначения: B(x,R) = { £ = (£ 1 ,^ 2 ) : | x — £ | < R } , D_a u(x,t ) — левая часть уравнения (1).

Задача (1) сводится к эквивалентной задаче для функции v(x,t) = u(x,t) — ^(x i ,t) :

□ av(x,t)= f (xi,t), v(x, 0) = ^i(x),   Vt(x, 0) = ^i(x),   v(xi, 0, t) = 0,(2)

где

^1(x) = ^(x) — д(Х1,0), ^i(x) = ^(x) — ^t(xi, 0), f (xi,t) = — Da^(xi,t).(3)

В свою очередь, решение задачи (2) представим в виде суммы решений двух более простых задач v = v i + V 2 :

• □    aV1 = 0, vi(x, 0) = ^1(x),        (x, 0) = ^i(x), vi(xi, 0,t)=0,(4)

∂t

• □    aV2 = f, V2(x, 0) = 0, ^(x, 0) = 0, V2(xi, 0, t) = 0.(5)

Для корректности задач (4), (5) необходимо добавить условия согласования начальных и краевых данных. Отметим, что уравнения в (4), (5) выполняются также и в граничных точках области G . Соответственно везде в дальнейшем будем считать, что

∂2ϕ∂

П (x i , 0) = 0, —^2-(x i , 0) = 0, ^ i (x i , 0) = 0,   —22-(x i , 0) = 0, f (x i , 0) = 0.

∂x2

Для исходных данных эти условия можно переписать в виде:

∂²ϕ 1

y(x i , 0) = ^(x i , 0), -dx2"(x i , 0) = 0, ^(x i , 0) = ^ t (x i , 0),

∂2ψ             ∂2µ dx2"(xi, 0) = 0, 'dt2"(x1’ 0) — a dx2(x1’ 0) = 0‘

2. Основной результат

Для решения задачи (4) используем известный метод отражения [3, с. 412]. Для этого функции ^ i (x) и ^ i (x) продолжим нечетным образом для Х 2 < 0 и обозначим эти продолжения через Ф 1 (x) , Ф 1 (x) соответственно. Принятые нами условия согласования обеспечивают принадлежность этих продолжений пространствам C 3 (D) , где D — любая ограниченная область переменных (x i , Х 2 ) . Тогда справедлива классическая формула Пуассона:

1 v i ^{( x,t )} = — 2па

д [ Ф(€) d€ + [     ^i(€) d€ dt     ^a^t2—]^—^       ^a2t2 — |€ — x|2

B(x,at)                             B(x,at)

Аналогичный подход будем также использовать для задачи (5). Рассмотрим два варианта продолжения функции f (x _i ,t) по x ₂ : F_i (x _i ,x ₂ ,t) = f (x _i ,t) при всех x ₂ ; F 2 (x _i ,x ₂ ,t) = f (x _i ,t) для x ₂ >  0 и F 2 (x _i , x ₂ ,t) = — f (x _i ,t) для x ₂ < 0 . Функция F 2 (x,t) оказывается нечетной по X 2 с возможным разрывом в точках (x i , 0) . Будем использовать функцию F 2 (x,t) в качестве правой части в задаче (5) вместо функции f(x i ,t) . Однако здесь мы не можем воспользоваться традиционным подходом, основанном на известной формуле Дюамеля, в которой предполагается гладкость правой части уравнения.

Для точек (x,t) , Х 2 > 0 , at > Х 2 определим множество B ^- (x,R) = { € : | x — € | < R, € 2 < 0 } , где R = a(t — т) , и интеграл

t - x 2 /a

J (x,t)= j J

0 B ^- (x,R)

^{f (€} i ^,T) d^€d^T ^ R² — | x — € | ² '

Лемма 1. Для точек (x, t), 0 C X 2 C at, функция J (x,t) имеет непрерывные частные производные до второго порядка включительно и удовлетворяет уравнению □ a J (x,t) = 0. Кроме того, на плоскости Х 2 = at функция J (x,t) и ее частные производные до второго порядка включительно обращаются в нуль.

<1 Функцию J(x, t) запишем в виде повторных интегралов:

t - x 2 /a   x 1 + ^√ R ² - x ² 2             0

f л f                 Г                    f(€ 1 ,т) d€ 2

J (x,t) =   I di                          —,                     =

J J_______ VR² — (€ 1 — x i )² — (€ 2 — X 2 )^{2 0}        x 1 - R ² - x ² ₂ x 2 - R ² - (ξ 1 - x 1 ) ²

Легко проверить, что

t - x 2 /a

J (x, t) = У di

x 1 + R ² - x ² ₂

j    f (€ i ,i)

arccos

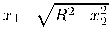
2 dξ .

R² — (€ i — x i )²

d€ i . (9)

Меняя в (10) порядок интегрирования, получаем

J (x, t)

x 1 + a ² t ² - x ² ₂

= L   d€i x1 - a2 t2 -x22

t - ^√ (ξ 1 - x 1 ) ² +x ² ₂ /a

/ f (€ , т) arccos —,        ² di.

0                        V R² — (€ i — x i )²

Теперь вычислим частные производные функции J(x,t). Заметим, что t —   (€1 — x1)2 + x2/а = 0,  ^i = x1 ±   a2t2 — x2,

а также arccos(x2/\/R2 — (€1 —x1)2) = 0 при т = t — (€1 —x1)2 + x2/а. Поэтому dJ (x, t) ∂t

x ₁ +^/ a ² t' 2 — x' 2       t — (§ 1 — x 1 ) ² +x 2 /a

=       [     d^i        [       f (6-> т )-^|-arccos —       x 2        dт

J _____   ¹ J                             R² — (^ 1 — X 1 )²

x i — V ^ ² 1 ² — x 2               ⁰

x i + д/a ² t ² — x 2

=   /

d£ 1

x 1 -   a ² t ² - x ² ₂

t — V (§ 1 — x i ) ² +x 2 /a

J

___________ f(€ 1 ,T) • a²(t — т ) • X2 ___________ ^ R² — (£ — X 1 )² — x 2 ( R² — «1 — X 1 )² )

dτ.

Внутренний интеграл в (12), с учетом равенства f (€ 1 , 0) = 0 , преобразуем при помощи интегрирования по частям и получим:

^{t —} V ⁽ § i ^— x i ^{) 2 +} x ^{2 /a}

/

___________f (€1,т) • a2 (t — T) • x2___________dT VR2 — «1 — X1)2 — x2(R2 — «1 — X1)2) T t—V(§1—x1)2+x2/a

= —      / R² — (^ — x ₁ )² d V R^{2 — (}^ ^— x^{1)2 —} x²

^{t —} V ci i — x i ^{) 2 +} x ^{2 /}a

• =       /       V ^{R2 — (}^ ^— x^{1)2 —} x² dT ( RR ² ——(6. — X 1 )² ) d ^T .

  
  

Поэтому x1+aJa212—x2     t—у/ (§1—x1)2+x2 /a d2J(x,t) _ ff dt*2            J_____d^1

x1 —Va2 t2—x’2

X

dt (V^{R2 (}^ x¹⁾² x² дт (r² f Й— )x 1 )²) ) d ^T ‘

Аналогичным образом получаем xi + Va212—x2     t—V(§1—xi)2+x2/a dJ(x,t) = Г                 Г _________f (£1,т)(^1 — X1) X2 dт_________ dx1          J 1 -I        VR2 — «1 — X1)2 — x2 (R2 — «1 — X1)2)

x 1 — ^/ a ² 1 ² — x 2                ⁰

x i +-^/ a ² 1 ² — x 2      t — у/ (§ 1 — x i ) ² +x 2 /a

=     /    d^ 1      /       V R² — (^ 1 — X 1 )² — x 2

x ₁ — V a ² 1 ² — x 2               ⁰

X

d /    f «1 ,т)« 1

дт V(R² — (€ 1 — X 1 )²)a^:

x 1

^)x 2 A ^{! (t — т} и

dτ,

-

d2 J (x, t)

x

dx 1

x 1 -   a ² t ²

1    d⁵¹

t - V ⁽ £ i - x i ) 2 +x 2 /a

/

^^^^^^^^r

_x 2 ₂

-

x

X

^d /     f⁽⁵ 1 ^,T)(5 1 - ^x 1 ^)x 2

дт (R ² - (5 1 - X 1 )² )a ² (t - т )

dτ,

x

d ²

dJ (x, t)

dx 2

-

x 1 -   a ² t ²

J (x, t)

xi+x0^2

dx 2

-

X i — ^V 0 2 t 2

d²J (x, t)

x i + v^

-

x

∂t∂x i

x 1 -   a ² t ²

-

x

j   d⁵

t—V^T—xD2+xI /a

/

f ⁽ 5 1 ,t ^{) dT}

-

x

-

x

R^

-

(5 1 - X 1 )²

-

^x 2 ’

-

x

d5 1

d5 1

t - V^-xo^ +x l ^/a

/

-

x 1 )²

-

x² ₂

X

d p (5 1 , т) дт a²(t - т )

dτ,

t - V (£ i — x i ) ² +x 2 /a

/

∂

∂x i

(x 2 ^R? - (5 1 - x 1 )

-

_x 2 ₂

Используя равенства (14), (16), (18), запишем

x i + л/аЧ²

x

где

∂

^X дт

t-V Ki- x i ) ^{2 + x} 2 /a

□ J (x,t) =

x 1 -   a ² t ²

-

x

I (x, t,

- a²

d5 1

(      f ( 5 1 ,t )

R² - (5 1 - x 1 )²

j        I ^{( x,t,5} 1 ^,T ) ^dT ,

=-- dt(-v'—- 4 "*;;iT ,))

dx - (x ₂ K(x,t,⁵¹ ,^T) A^

f (5 1 , T )(5 1

-

x x )

a²H^(x,t,5 1 ^{,T )( t - T})

dτ.

+ a2

dx 2 O' (x't'5-т) dT(oPy)).

V^(x ,t^,5 1 ,^T) = VR^{2 - (5} 1

-

x 1 )²

-

_x 2 _{2 ,}

H (x,t,5 1 ,T ) = R²

-

(5 1 - x 1 )²-

Опуская для краткости аргументы функций, прямыми вычислениями убеждаемся в том,

что

I = V

f

∂t∂τ H

д2

+ V

- - ц

(5 1 - x 1 )²

f

(t - T)H

-

V∂ ∂τ

f

(t - T

-

dx 1 дт

(5 1 - x 1 )f (t - T)H

) + » 2 - T) ЦГ) - dT(tf:))

)h)

_a 2 _f

+--- =

⁺ VH

-

∂ dT   (t

Vf

-

τ

) h •

Обратимся теперь к равенству (20). Заметим, что V(x,t,€ 1 , t — ^ (€ 1 — x i )² + x 2 /a) = 0 и f (€ 1 ,0) = 0 . Таким образом, оказывается, что подынтегральное выражение в (20) оказывается производной по τ от функции, обращающейся в нуль в верхнем и нижнем пределах интегрирования по т . Следовательно, Da J (x, t) = 0 .

Теперь докажем остальные утверждения леммы. Что касается непрерывности функции J (x,t) и ее производных, то это свойство является прямым следствием формул (9), (12)-(19). Осталось доказать обращение в нуль на плоскости Х 2 = at функции J (x,t) и ее производных. Отметим, что t — т ^ const > 0 и H ^ const > 0 при Х 2 ^ 5 >  0 . Поэтому в формулах (9), (12)-(19), представляющих функцию J (x, t) и ее производные, неограниченными множителями подынтегральных выражений могут быть только функции 1/V , интегралы от которых по т ограничены по модулю единым числом. Поскольку при at — Х 2 ^ 0 промежуток интегрирования по € 1 стягивается в точку, соответствующие интегралы стремятся к нулю, что и означает справедливость доказываемых свойств при Х 2 ^ 5 > 0 . В силу произвольности 5 , указанные свойства, а следовательно, и лемма 1 доказаны полностью. >

Теорема 1. При сделанных предположениях существует единственное решение за дачи (1), которое представляется в виде

1 d [ sg^n(€2) Ыб.’ | <2|) ^— Ж1’⁰⁾) d^€ u(x,^t)= ^t) ⁺ —dt J ------ _{V a} 2 t 2 - | € - x | 2------

B ( x,at )

+ 1      [ ^sg^n(€ 2 ⁾ ( ^^(€ 1 , ^|€ 2 1 ) ^— ^ t ^(€ 1 ,⁰⁾ ) d^€

⁺ 2na J           ^a ² t ² — | € — x | ²                             (24)

B ( x,at )

, ¹ f. (         Sgll({ 2 ⁾        / ^дМСт)    2 ^dW 1 ,T) V,

⁺2паГ^т J    _v „ 2 ₍ t — т) 2 — | ; — x | 2 (——⁺ -_:

0     B(x,a(t - T))

<1 Будем использовать функции F 1 (x,t) , F(x,t) , введенные после формулы (7). Рассмотрим интеграл типа Дюамеля при at > Х 2

t

U _м =     [ dr   [    _/2 /2 «;) de ,           (25)

^2na J        J     “(t (t — т )² — | € — x | ²

0     B(x,a(t - T))

который можно представить в виде

t

и (xt) = J_ [      [ _r F 1 ^(€ т ) d^€       — 2J

’       2n“                     _a 2 (t — т )² — | € — x | ²       2na ’           ‘ '

0     B(x,a(t - T))

где функция J(x,t) определена равенством (8). Свойства второго слагаемого в правой части (26) указаны в лемме. Что касается первого слагаемого, то мы не можем считать его классическим интегралом Дюамеля, поскольку функция F1 (x, t) имеет непрерывные производные только первого порядка. Однако то обстоятельство, что F1 (x, t) не зависит от Х2, позволяет методом спуска убедиться в том, что этот интеграл есть решение уравнения в (5). Поэтому DaU(x,t) = f (x1,t). Заметим, что при Х2 = 0 интеграл U(x,t) = 0, вследствие нечетности подынтегральной функции и симметрии области интегрирования по £2- Также нетрудно видеть, что U(x, 0) = Ut(x, 0) = 0. Если продолжить нулем функцию J(x,t) для at ^ Х2, то, вследствие доказанных в лемме свойств функции J(x,t), функция U(x,t) оказывается решением задачи (5). Учитывая редукцию задачи (1) к задачам (2), (4), (5), складывая полученные решения и выражая в формулах (7) и (25) подынтегральные функции через исходные данные задачи (1), получаем формулу (24).

Докажем теперь единственность решения задачи (1). Напомним, что уравнение □ _au = 0 выполняется также и в граничных точках. Возьмем два решения этой задачи U 1 и U 2 . Их разность w = u i — U 2 удовлетворяет равенствам Da w = 0 , w(x, 0) = w_t(x, 0) = w(x i , 0,t) = 0 , вследствие чего функция w(x,t) и ее вторая производная по Х 2 равны нулю при Х 2 = 0 . Поэтому нечетное продолжение функции w(x, t) по Х 2 оказывается классическим решением задачи Коши для уравнения Da w = 0 с нулевыми начальными данными. В силу единственности решения такой задачи, w = 0 . Таким образом, теорема доказана полностью. >

Еще одним отличием нашей работы от упомянутых выше [1, 2] является наличие простой формулы (24), позволяющей легко построить численный алгоритм. Кроме того, важно отметить, что подобные явные представления широко используются в теории обратных и условно-корректных задач. В подтверждение этой связи укажем на многочисленные публикации, которые можно найти, например, в списках литературы монографий [11–13].

В заключение обсудим некоторые аспекты выполненного исследования. Как видно, основная часть работы посвящена анализу интеграла типа Дюамеля, определенного формулой (25), где используется функция F 2 (x i , Х 2 , t) , вообще говоря, разрывная при Х 2 = 0 . Соответственно, статью можно было бы назвать «Обобщенный интеграл Дюамеля», однако в нашем случае функция F 2 (x i ,x 2 ,t) оказывается кусочно-постоянной по Х 2 , что снижает общность исследования. Это обстоятельство вызвано тем, что мы рассматривали случай нулевой правой части уравнения в (1). Было бы интересно исследовать и более общий случай.