Формулировка некоторых самосогласованных задач радиоэлектроники

Самосогласованную систему можно определить, как замкнутую систему, в которой первичные источники корректируются обратным воздействием на них вторичных источников. В стационарном состоянии такая система описывается однородной краевой задачей либо на дифференциальном, либо на интегральном уравнении (системе уравнений, в общем случае интегро-дифференциальных), то есть задачей на собственные функции и собственные значения. Понятие «самосогласованная краевая задача» идет из физики твердого тела [1].

Сформулируем такие задачи для различных электромагнитных явлений, так или иначе связанных с диапазоном СВч, со строгой постановкой задачи генерации и излучения.

Рассмотрим подходы к формулировкам самосогласованных задач из области электромагнетизма.

увилля. Указанное уравнение Гельмгольца записываем в виде:

L У = 0,                                         (1)

где дифференциальный оператор L , записывается как L = А + к 2 ; к = Юл/бц .

Под у можно понимать функцию, через которую вычисляются все компоненты поля внутри области V . В частности, при определенных условиях это может быть одна из компонент векторов Герца. Так, например, если область V представляет собой отрезок продольно-регулярного волновода, в качестве функции у можно взять продольную компоненту одного из векторов Герца – электрического или магнитного.

Для двусвязной области V запишем формулу Грина:

[ ( у LG - GL у ) dV = (6 (у — - G —) dS,     (2)

d n    dn

VS где S = S - Sqn, n — внешняя по отношению к области V нормаль; G – функция Грина, удовлетворяющая уравнению:

LG = А G - к ² G =5 ( r - ^ ) ,                 (3)

в котором r — точка наблюдения, ?q — точка особенности функции Грина.

Используя (3) и свойство дельта-функции, получаем:

/ _—         д G ~ ду ^,

у ( r ) = (у - G ) dS .                     (4)

д n    д n

S

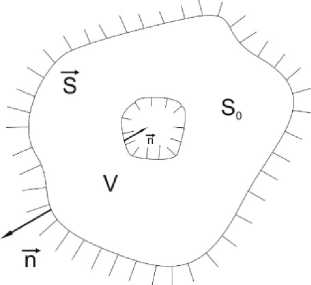
Рис. 1. Область V , изнутри ограниченная поверхностью S ₀ , снаружи – S

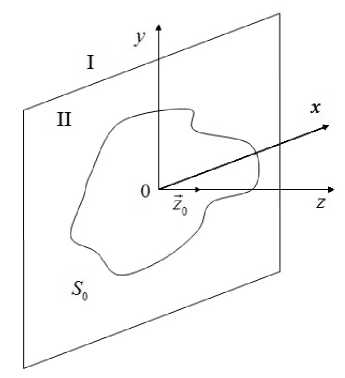
Рис. 2. Излучающая поверхность S ₀ которое в антенных задачах позволяет однозначно определить поле излучения апертурных антенн. Собственные функции как решение однородных краевых задач должны удовлетворять этому условию, то есть поле излучения антенн должно формироваться из этих функций. Проверка выполнения условия (8) является обязательной, поскольку для эллиптических уравнений, к которым относится уравнение Гельмгольца, задача Коши для открытых областей не является корректно поставленной.

Обозначая функцию поля у на поверхности S как Уо и удаляя поверхность S в бесконечность, переписываем (4) в виде:

у ( r ) = ф(у| ^ - G ^dS .               (5)

д n    д n

S

Положив Г о = 0, берем в качестве функции G функцию Грина свободного пространства:

1 e - ikr

G =--.

4п г и этом из (5) получаем выражение для функции поля у (г ) в произвольной точке свободного пространства как интеграл от Уо по поверхности, ограничивающей это пространство изнутри:

V⁽ r ) =   ф [у о

4п      д n

S 0

( -ikr Л e

г

-

ду о д n

- ikr Л e

r

^r ] dS .

Выражение (6) называется интегралом Гюйгенса — Кирхгофа. Положив r = r s , получаем интегро-дифференциальное уравнение относительно функции Уо поля на поверхности S o :

Уо ^{( r ) =} $ 1- [V o 4п     д n

f - ikr Л e

-

r

^{дУ о} e-ikr ] dS r .  (7)

д n    г

S о              ^{7      7}

оно является математической интерпретацией самосогласованной задачи по нахождению

функции поля по распределению этой функции на поверхности, ограничивающей рассматриваемое пространство. Как видно из (7), самосогла-

сованная задача приводит к однородному интегральному уравнению Фредгольма 2-го рода, то есть является задачей на собственные функции и собственные значения, найдя которые, по формуле (6) можем определить функцию поля в произвольной точке пространства V .

Формула (6) приводит к условию излучения:

г 2      ⁵

lim г у о — г ^^      д n

( - ikr Л e г .

^д У о д n

( -ikr Л e

= 0.

r

2. Самосогласованная задача об излучении

Сформулируем самосогласованную задачу об излучении, собственные функции которой являются базисом для внешней краевой задачи [7] на неоднородной системе уравнений Максвелла с краевыми условиями на внутренних поверхностях и условием Зоммерфельда на бесконечности. Полученный базис используется для представления поля, создаваемого заданным источником, то есть для решения антенной задачи в строгой постановке [8].

Одной из базовых антенных задач является задача об излучении с конца круглого экранированного волновода с фланцем. частным вариантом такой задачи является задача об излучении из круглого отверстия в идеально проводящем экране [9]. Само отверстие является излучающей апертурой, экран имитирует фланец. При этом, однако, не учитываются токи, затекающие за фланец, то есть конечные размеры последнего. Другой типовой задачей является задача об излучении с конца открытого диэлектрического волновода (ОДВ). Формально для решения обеих задач можно воспользоваться общей формули-

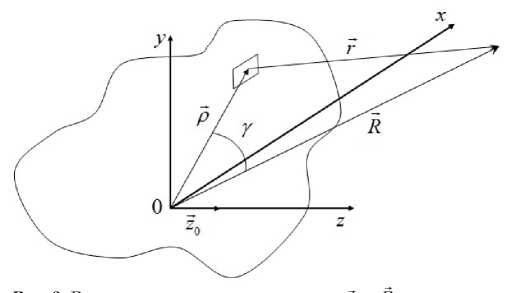
Рис. 3. Взаимное расположение векторов р и R , определяющих, соответственно, положение элементарного тока на поверхности S ₀ и точку наблюдения

- ikr

A^m = A [ z o , E ]---- dS ,                 (14)

4n             r

S 0

которые записаны с учетом (9).

Тангенциальные компоненты полей в области

II (рис. 2) вычисляются по формулам [13]:

4"» =

R R (^П) =

—i ю A +— rotA , z o s

i ю A ^m

1      ^— e —

+— rotA , z o . u

ровкой самосогласованной задачи об излучении. Излучающую поверхность, которой является торец ОДВ или металлический экран с отверстием, представляем как плоскость S ₀, по которой протекают электрические и магнитные токи с плотностями j e и j^m , соответственно (рис. 2).

Согласно принципу Гюйгенса – Френеля [2] плотности поверхностных токов на S ₀ связаны с полями соотношениями:

^— e =[ ^— o , н ], ^— m =-[ z o ,E i ]. (9)

В однородной среде векторные потенциалы,

На излучающей поверхности S ₀ должны выполняться граничные условия:

(ⁿ)          —          — (ⁿ)|

E T       E T , ^H T       H T       ,               ⁽¹⁷⁾

^S 0          S 0         ^S 0           S 0

где EE _T и H _T — это поля на поверхности S o , связанные с токами на этой поверхности соотношениями (9).

Подставляя в граничные условия (17) компоненты поля (15) и (16) в области излучения II, получаем с учетом (13) и (14):

—►

E T

-

—*

4п

i юц

I Й T

e

- ikr

dS +

создаваемые электрическими и магнитными токами, удовлетворяют волновым уравнениям [10]:

—       Я2 A e—

AAe su' „ = -цje,(10)

d t ²

Я2 A m1

AAm su' „ = sjm,(11)

d t ²

S 0

r

+ rot

I ^E

e

- ikr

r

dS , ^A o

,

^

—*

—►

H

T

решения [11; 12] которых имеют вид:

A

A

P e 4n

V

——

- ikr e

r

dV ,

A m

-

-  1 m

4n

——

- ikr e

V

r

dV ,

4n

(

+ rot

i ЮБ

I E

S 0

T

e

- ik r

dS +

r

IZ H-

T

e

- ik r

—*

I ^S o

r

dS , z o

/

.

Уравнения

(18) образуют систему двух век-

торных интегральных уравнений относительно

где r — радиус-вектор, соединяющий элементарный ток на поверхности S ₀ с точкой наблюдения; R — — радиус-вектор точки наблюдения (рис. 3). Модули векторов Г и R — связаны соотношением:

r = Jр2 + R2 - 2рR cos у , где р — модуль радиус-вектора р элементарного тока на поверхности So; у — угол между векторами р и R (рис. 3).

В том случае, когда поле излучения создается поверхностными токами, векторные потенциалы (12) вычисляются по формулам

-

A ‘ = rJ[ Z o, H ] e

4п

S 0

ikr dS ,

r

тангенциальных компонент электрического и магнитного полей на излучающей поверхности S ₀. Как видно из (18), интегральные уравнения однородные. Таким образом, имеем задачу на собственные функции и собственные значения. Такая задача, сформулированная в виде замкнутого цикла (поле излучения вычисляется через неизвестное поле на поверхности излучения и подставляется в граничные условия на этой поверхности), называется самосогласованной. В ней отсутствует заданное стороннее поле. Задачи, в которых это поле присутствует, приводят к неоднородным интегральным уравнениям. Такие задачи не следует классифицировать как самосогласованные.

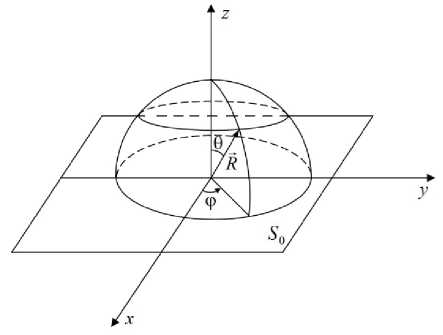
Рис. 4. Связь декартовых и сферических координат, определяющих положение точек пространства над излучающей поверхностью

Используя свойства дифференциальных век- торных операторов, граничные условия, связь декартовой и сферической систем координат (рис. 4), получаем две системы уравнений:

2 п ю

E P =

—

^ tn^ jj H .

2 п ю

H ф =

—

^JJ E P

e ^— ikr o

-----p dp d ф o, ro e—ikro

-----p d p d ф _o .

ro

2 п ю

E ф =      I H

0 0

2 п ю

H p = В J E

I                 0 0

e ^— ikr o

-----p dp d ф o, ro e—ikro

-----p d p d ф _o .

ro

Отметим, что система (19) может быть полу- чена из системы (20) (и наоборот) с помощью перестановочного принципа двойственности

^ p <-------- p, ф <--------^ ф, r <-------- ^, что подтверждает корректность их (систем) вывода.

Компоненты поля в (19), (20) подвергаются автономным разложениям, коэффициенты которых определяются из совместного решения систем интегральных уравнений (19), (20). Собственные значения задачи находятся как совместные решения двух характеристических уравнений, получаемых в результате алгебраи-зации систем (19), (20).

• 3.    Автогенератор на СВЧ-триоде с учетом пролетных явлений

Главным признаком самосогласованных задач является учет в них обратного влияния на функцию источника физического феномена,

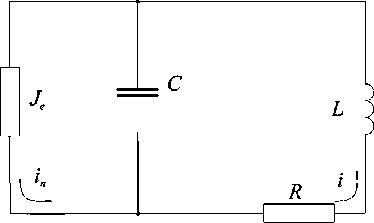
Рис. 5. Эквивалентная схема сеточного контура

du i = C— + i

dt

n

d ² u

du

"T^ ^{+ s} ® 0 "T7 dt ²         dt

—

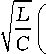
di_n      2

^ю 0 -ТГ ^{+ s} ® 0 in dt

Так как обычно Q » 1, будем полагать б ^ 1. Тогда решение уравнения (1), считая его близким к синусоидальному, ищем в виде:

u = x (t) sin у (t), (22) где у (t) = toot - 0 (t); x (t), 0 (t) медленно меняющиеся во времени функции, удовлетворяющие предельным соотношениям:

lim x ( t ) = u = const;

б^О ^v ’    ⁰

t ^ю lim 0 (t) = 0 = const б^О v '    0

t ^ю

для того, чтобы решение (22) в пределе б ^ 0, t ^ ю имело вид u = u sin (toot -0о).

обходимо выполнение условия:

lim i n = 0.                                       (24)

б^О

Последнее будет выполнено, если представим наведенный ток в виде разложения по малому параметру:

i n = i n 0 ^{+ б} i n 1 ^{+ б} i n 2 ⁺ —

В уравнении (21) пренебрегаем, учитывая (24), членом -JL / C БЮ о2 i n , как имеющим второй порядок малости. Уравнение принимает вид:

Учитывая, что постоянный положительный потенциал в плоскости сетки Vo ^ x(t), пренебрегаем влиянием пространственного заряда в пространстве сетка-катод. Пролетные эффекты в промежутке сетка-анод можно не учитывать, ввиду больших скоростей электронов на этом участке, поэтому наведенный ток в цепи анода можно считать равным электронному в цепи сетки. Наведенный ток в цепи сетки in = In + ia , (27) где In – наведенный в цепи сетки ток, без учета удаляющихся от сетки электронов.

Рассматривая движение электронов в промежутке сетка-катод, можно получить выражение для 1-й гармоники I_n :

I n ⁽¹⁾ = X 1 (ф o )sin to o t + N 1 (y o )cos to o t , (28) где ф о = to o d / V o средний пролетный угол; v ₀ = V n V o /2; d – расстояние между сеткой и катодом; n — удельный заряд электрона.

При получении выражения (28) учитывалось, x ( t ) , 0 ( t ) — медленно меняющиеся функции. Всеми членами, содержащими ц в степени вышей третьей, пренебрегли.

Считая, что электронный ток в плоскости сетки d2u     du

ТУ ^{+ бЮ} О у dt ² dt

-

M to o ²

di

ТУ ^{+ ю}0 ^u = dt

-

бю

L ( di n 1 ^ V C V dt J.

В (25) ограничились первым членом разложения. Правая часть в уравнении (25) учитывает обратное влияние на первичное генерируемое напряжение.

Таким образом, задача об автоколебаниях в рассматриваемой структуре может оставаться самосогласованной и при отсутствии конструктивной обратной связи, то есть при M = 0. Решая уравнение (25) методом укороченных уравнений [13], сводим его к системе двух уравнений:

— = M to₀ ^ a cos у ( t ) - бю₀ x ( t ) cos² у ( t ) - dt         dt

L (di ^       , x

УЫ у I^cos У⁽ t ) , V C V dt J

d 0   M to di            1

=    0 ТУ sin y( t )-тБЮoSin2У( t)- dt   x (t) dt            2

^^ ( di ^ -^k^n¹ 1 ^sin y⁽ t ) .

V C V dt J

. _ . 1 дф in i0 [1 d (ю0 t)] , где ф = ЮоТ (т — время движения электрона до сетки), получаем в первом приближении выражение для первой гармоники анодного тока ia(1) = Цio[pз(Фo)sin ю01 + Qз(Фo)cos ®ot], (29) где Вз(Фо) = sin Фо - Фо cos Фо; Qз(Фo) = Фо sin Фо + + cos Фо - 1.

Ограничимся первым приближением в разложении i_a , поскольку второе приближение не дает дополнительного вклада в 1-ю гармонику, а третье существенно мало по сравнению с первым.

Выше на наведенный ток i_n было наложено условие (24). чтобы это условие выполнялось, необходимо в силу равенства (27), выполнение подобных условий для токов I_n , i_a , т. е. необходимо положить для этих токов возможность разложений, подобных (24). Только в этом случае в пределе, когда б ^ 0, t ^ ю, мы получим чисто синусоидальное решение. Подставив (28) и (29) в уравнения (26), после усреднения по периоду T = 2п / к> о , получаем:

dx = ¹ БЮ о {а о [ S 1 x ( t ) - S 2 x ³ ( t ) ] - x ( t ) }, (30) dt 2

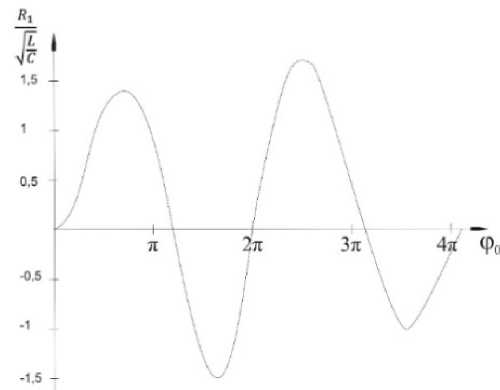
Рис. 6. Функция, определяющая устойчивый режим автогенератора

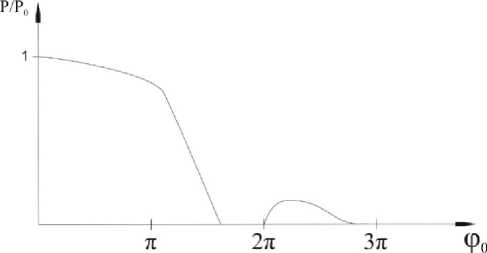
Рис. 7. Экспериментальная зависимость мощности автогенератора от среднего угла пролета d' в I Ki + K2x (t) + K3x3 (t )f.

dt I x ( t )

Исходя из уравнений (30), рассмотрим условия самовозбуждения и устойчивости автогенератора. Представив амплитуду колебаний в виде:

x (t) = u 0 + ^( t) , где^( t) – малая случайная величина, из первого уравнения (30), получаем условие самовозбуждения a0 51 > 1                                          (31)

и условие устойчивости a0 (51 - 352u02)< 1.                              (32)

Очевидно, что условие устойчивости будет выполняться лишь при 5 2 > 0. Из графика функции R 2 ( ф о ) = 32 V o2 5 2 (рис. 6) видим, что существуют определенные области значений пролетных углов, в которых нельзя обеспечить устойчивый режим работы автогенератора.

Первая такая область при ф о > п. При ф о > 2п возможна устойчивая генерация.

Работа генератора при больших углах пролета проверялась на триоде ГИ-7Б с увеличенным

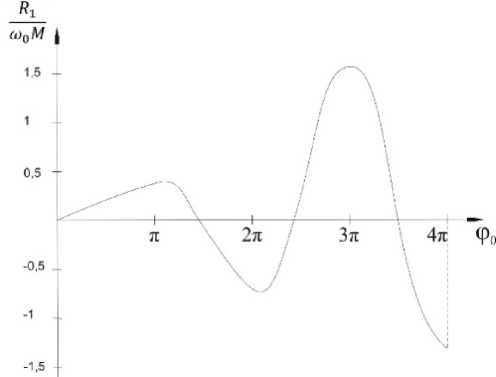
Рис. 8. Функция, определяющая условие самовозбуждения расстоянием сетка-катод. Полученная при этом зависимость величины генерируемой мощности от угла пролета (рис. 7) показала, что за пределами ф о = п. Наблюдается резкий спад мощности, а затем – полное исчезновение генерации. За пределами ф о = 2п Возникает новая зона генерации с более низким уровнем генерируемой мощности.

Рассмотрим условие самовозбуждения. В генераторе величина S ₁, в основном, определяется членом Юо MP 3 . Изменяя величину обратной связи, можно, вообще говоря, всегда добиться выполнения неравен ства ( 31). На рис. 8 представлена функция R = L / СР з(Фо).

Сопоставляя R ₁ и R ₂, видим, что существуют такие области значений угла пролета, в которых можно добиться выполнения условий (31) и (32) даже при M ^ 0, то есть при отсутствии конструктивной обратной связи. В этом случае обратная связь осуществляется через электронный поток, а самосогласованность задачи обеспечивается наличием в уравнении (25) правой части, изменяющейся во времени синхронно с генерируемым напряжением, что делает автоколебания присоединенными к источнику (в данном случае к электронному потоку), а уравнение (25) присоединенным к уравнению автоколебаний.

• 4.    Возбуждение открытого резонатора электронным потоком

Рассмотрение сочетания высокодобротной квазиоптической системы с электронным пучком представляет интерес в связи с тем, что такое сочетание может быть использовано при построении высокостабильных СВч-генераторов

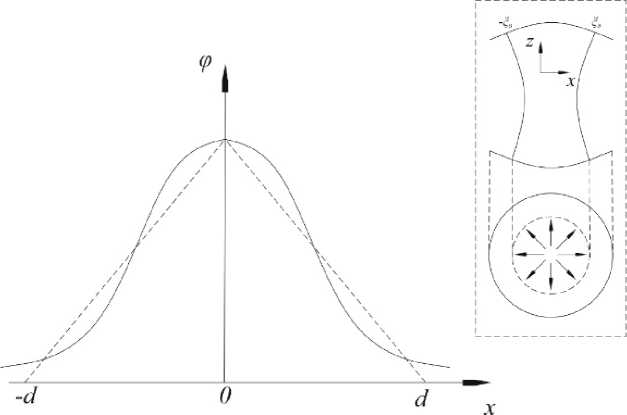
Рис. 9. Поле основного собственного колебания открытого резонатора

с низким уровнем частотных флуктуаций, а также при разработке генераторов, работающих в верхнем участке СВч-диапазона, когда возникает проблема разрежения спектра создания колебательных систем.

Как известно [14], при определенных достаточно больших углах пролета мощность наведенного тока, создаваемого электронным потоком, проходящим через промежуток переменного электрического поля, может быть отрицательной, т. е. возможно самовозбуждение СВч-резонатора, включающего в себя этот промежуток. В предыдущем разделе показано, что в триодном СВч-генераторе в результате возникновения областей отрицательной мощности наведенного тока (для промежутка сетка-катод) возможно самовозбуждение автогенератора при сколь угодно слабой конструктивной обратной связи, а при определенных условиях и без нее.

Основное колебание в резонаторе со сферическими конфокальными зеркалами описывается потенциальной функцией, имеющей гауссово распределение, рис. 9. После этого колебания заключено, как показано на том же рисунке, между каустиками ±^ о . Тонкий электронный пучок пропускается вдоль оси x в фокальном пятне резонатора, т. е. при z = 0. Этот пучок ускоряется постоянным электрическим полем, создаваемым напряжением 2 U ₀, приложенным к промежутку ( ^- ^ 0 , ^ 0 ).

Рассмотрение движения электронов в поле, имеющем гауссово распределение, приводит к сложному нелинейному уравнению. Для упрощения расчетов аппроксимируем гауссово распределение линейно (рис. 9). В этом случае электроны проходят два промежутка со взаимно

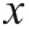
I Tbq

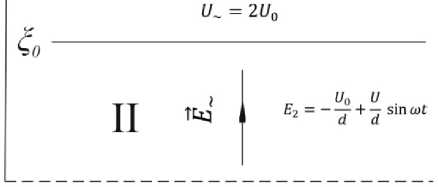
ll = о

Рис. 10. Аппроксимированное поле в фокальном пятне открытого резонатора противоположными переменными во времени и однородными в пространстве полями (рис. 9). Однородным в пространстве поле можно считать потому, что электронный пучок очень тонкий. Во всех дальнейших рассуждениях полагаем также выполненным условие

U 0 » U ,

где 2 U – амплитуда переменного напряжения в промежутке (-^ о , ^ о ).

Рассмотрим сначала первый промежуток (рис. 10). Интегрируя уравнение движения электрона, получаем выражение для скорости:

,   х      Un , х   П U, v (т, t) = п —0 (t - т) +--(cos ют - cos tot).(34)

7   7      d 7   ю d и координаты электрона

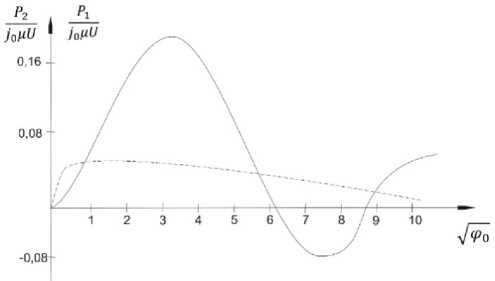
Рис. 11. Мощность наведенного тока в области фокального пятна открытого резонатора (сплошная линия – в 1-м промежутке; пунктирная – тока во 2-м промежутке)

F 2 = Ф 2 F '( Ф о ) + 2 Ф 12 F "( Ф о ) ;

Ф о ,Ф 1 , Ф 2 — - коэффициенты разложения (37).

Воспользовавшись разложением (38), после некоторых преобразований получаем в первом приближении выражение для скорости электрона в конце первого промежутка v (т, тd ) =

_ 2tod

ДфФ где

,

^{( т} , t ) = ^ d ^ 2 t ^{-т )} 2 +

+ -Ду— (to (t - т) cos гот - sin tot + sin ют). to2 d где т — время влета электрона; t — текущее время; n = |е / m| (e, m — заряд и масса электрона).

Первый промежуток электрон проходит за время: T 1 = т d - т, где т d — время выхода электрона из этого промежутка. Подставив в уравнение (35) t = т d введя обозначения:

2_т2       _ to d

^Ф = ^to T i ; ^Ф о = ———, n U о

Ф = го ² т d ²  2 U = ц

U ₀

получаем уравнение относительно ф:

Ф = Ф о - ц[ДФ cos( Дф - ДФ) -

- sin Дф + sin(Дф - Дф)].

Величина © = фф — угол пролета в первом промежутке. Подставив ф в виде ф = фо + цф1 + Ц2ф2 + —                      (37)

и разложив правую часть уравнения (36) в ряд по степеням малого параметра ц, приравниваем в (36) коэффициенты при одинаковых степенях ц. В первом приближении:

Ф = 2—— + ц[sin Дф-П ^U о

- ДФ Д cos(Дф - Дф ф ) - sin( Дф - ДФ Ф )].

функция ф удовлетворяет уравнению Лагранжа (36), поэтому любую функцию F ( ф ) можно представить [14] как

F ( ф ) = F + ц F i + ц² F 2 + —, (38)

где

F = f ( Ф о ) ;    F =Ф 1 f ‘ ( Ф о ) ;

M =

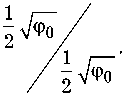
Вычислим наведенный ток при прохождении электронами первого промежутка:

t

In (t)= j°      v (т, t)dт = jо-{ф + ц[sin ДФ" + d т=t-T            Фо                   (4о)

+ sin(Дф - Дф)] - Дф cos Дф}, где j0 – величина постоянного электронного тока, поступающего в первый промежуток.

Воспользовавшись разложением (38) и ограничившись первым приближением, получаем

I a ( t ) = j о ^{{1 +} -1= ^{[2(1 - cos} Ф о ) ^- ДФо

- ДФ Ф sin Дф ф ] sin to t + i— [2 sin Дф ф -Ф о

- ДФ Д (1 + cos ДФ Д ] cos to t ].

Подставив (41) в интеграл

2 n

P1 = — J In (t) U sin totd (tot), о находим среднюю за период мощность наведенного тока в первом промежутке:

P 1 = j g ^ U [2 ( 1 - cos Ф о ) - ^Ф о sin фф ф ].       (42)

² Ф о

На рис. 11 представлена зависимость мощности наведенного в первом промежутке тока от среднего угла пролета Дфф .

Интегрируя уравнение движения электронов, получаем скорость в текущий момент t v (t, тd ) = v (т, тd ) + [Uо (t - тd ) +

U,                 _1Ч                         (43)

+ (cos tot - cos готd I —, tod где тd — время влета электрона во второй промежуток.

Как видно из (43), скорость электрона во втором промежутке в любой момент времени t зависит от момента влета электрона в первый промежуток т.

Считая, что электрон проходит 2-й промежуток за время T ₂ и интегрируя уравнение (43) по т d пределах [ t - 7 2 , t ], получаем:

а = j 7^0 + ЦF (а) + F2 (а), (44) где а = toT2 — угол пролета во втором промежутке. Представив угол пролета а в виде а = ад + ца + ц а2 + ... , (45) разлагаем правую часть уравнения (44) в ряд по степеням малого параметра ц, точке а = ад. Приравнивая в (44) коэффициенты при одинаковых степенях ц, в первом приближении получаем

2ю² d ² Г CToOn U O ^а 0                I ^{1 +}              1

УФо n U 0 и   2to² d ²

_а =      F 1 ^(а 0 )     .

Ф о n U о ^а о 2to² d ²

По аналогии с первым промежутком получаем, в первом приближении, наведенный ток во вто- ром:

I n ( t ) = 1 0 ( t ) + Ц I 1 ( t ) ,

Средняя за период мощность 1-й гармоники наведенного тока во 2-м промежутке:

p _ j o 1 7°0 U ²

P2 = -/=)---(cos а0 - 1) + nu Q1 +    /— TT—(Q2 + Q3)

⁺ "2"       1 . У Ф 0 n U 0 ^а 0

[              2to² dd^

Так как

(

\

)

-1

Ф 0

/

полученное выражение (47) представляет собой зависимость P2 (@0), изображенную на рис. 11 (®0 = УФУ). Из этого рисунка видно, что в интервале @0 е [6, 3 ^ 9] мощность наведенного тока в 1-м промежутке – отрицательная. Мощность наведенного тока во 2-м промежутке при этом – положительная, но по абсолютной величине она меньше мощности в 1-м промежутке. Это является демонстрацией физического варианта самосогласованной задачи. Электронный поток модулируется СВч-полем, а результирующая отрицательная мощность наведенного тока свидетельствует об обратном влиянии поля на ток, создающий его. Отрицательная мощность наведенного тока может трактоваться как отрицательное сопротивление в эквивалентной схеме автогенератора, наличие которого говорит о возможности выполнения условий самовозбуждения и устойчивости автоколебаний в системе без конструктивной обратной связи. Отсюда следует, что в указанном интервале можно ожидать возбуждения открытого резонатора немодулированным извне электронным пучком, введенным в его фокальное пятно. Полученный результат свидетельствует о том, что при сочетании электронного пучка с открытым резонатором представляется возможность создания автогенератора СВч нового типа. Такой генератор должен иметь высокую длительную стабильность по частоте, поскольку в нем электронная и резонаторная части разделены. Стабильность такого генератора будет в основном определяться добротностью открытого резонатора. Ориентировочно при добротности резонатора Q ~ 2 ■ 105 стабильность в течении часа должна быть не хуже 10-7.

Таким образом, показана возможность реализации физической постановки самосогласованной задачи, когда замкнутый цикл образуется самим электронным потоком, который модулируется СВч-полем, на которое, в свою очередь, оказывает обратное воздействие электронный поток.

• 5.    Задача на присоединенном уравнении Гельмгольца как самосогласованная.

Как показано в работах [3–6], в экранированных волноводах с неоднородным заполнением наряду с собственными волнами могут существовать присоединенные к источнику несобственные волны, описываемые краевыми задачами на присоединенном уравнении Гельмгольца, под которым понимается уравнение с правой частью, являющейся решением однородной краевой задачи на том же самом уравнении, но с нулевой правой частью. Такие краевые задачи являются самосогласованными, поскольку в них учитывается обратное влияние возбуждаемого поля на первичный источник и волновые числа в функциях поля и источника совпадают. Источники указанного вида можно классифицировать как источники типа бегущей волны, находящейся в синхронизме с возбуждаемым ей полем. Постоянная «подпитка» поля распределенным (бегущим) источником приводит к его (поля) линейному нарастанию в направлении распространения. Возникает эффект, подобный взаимодействию волноводного поля с полем пространственного заряда, наблюдаемый в лампе бегущей волны. Можно предположить, что эффект возбуждения распределенным источником присоединенной волны должен наблю-

В (51), (52) штрих означает дифференцирование по радиальной координате r.

Правые части уравнений (52) – решения краевых задач Дирихле и Неймана на однородном дифференциальном уравнении:

1 f .

R "( r ) + - R ‘ ( r ) + a' r

^^^^^^B

_ 2 ^

— R ( r ) = 0, r

даться не только в неоднородных направляю-

щих структурах.

Рассмотрим круглый экранированный волновод. Сформулируем для него присоединенную краевую задачу. Она состоит [3; 4] из уравнения:

совпадающим с уравнением Бесселя. Уравнение (51) в отличие от (53) называем присоединенным уравнением Бесселя. Его запись в виде (52) соответствует задачам Дирихле и Неймана, с решениями (50). Значения a ^e ’ m в уравнениях (52) находятся из граничных условий (49).

Решения уравнений (52) имеют вид:

Yn (ar)R(ar) , .

p ( ^a r ) = - J - ( ^a r ) J —           ^a ( ^a r ) +

W (ar)

д2пe,m 1 дпe,m   1 д2пe,m д2пe,m z1z1z1z+ д r2     r д r     r2 дф2       д z2         (48)

+ БЦЮ2Пzm = Ae,mJ- (ae,m r) cos -фe-iez, которое называем присоединенным уравнением Гельмгольца, и граничных условий:

дп e,

П e ( r = a ) = 0;   z ( r = a ) = 0,               (49)

д r соответствующих задачам Дирихле и Неймана. В (48), (49) Пz’m - продольные компоненты электрического и магнитного векторов Герца; J- (ae’m r) - функция Бесселя; a — радиус волновода; ae и am - корни уравнений (49).

Запишем решения вышеуказанных краевых задач в виде:

Ju (ar)R(ar) , .

+ Y - ( a r ) J -n           a ( a r ) ,

W (ar)

где R ( a r ) — решения уравнения (53), соответствующие краевым задачам Дирихле и Неймана; W ( a r ) — вронскиан, записываемый как

'

W ( a r ) = J_n ( a r ) Y_n ( a r ) -

' 2

^- J - ( ^{a r} ) Y - ( ^{a r} ) = —; na r

Y_n ( a r ) — функция Неймана. В (54) p ^e , m (a ^e , m r ) соответствуют задачам Дирихле и Неймана.

Подставляя (50) в уравнения (48), получаем:

C^e , m j J - (a ⁶ , m r )

+ r J - ( a ^e , m r ) +

+

e , m ^п z

C^e , m J_- ( a ^e , m r ) + D , m

(a ⁶ , m ) 2

n

-

J

n

( a em r )

+

e,m       e,m e,m x Jn (a , r) + p , (a , r

•) cos - ф e i ^{в z} ,

+ D e , m j j - ( a ^e , m r ) + r J - ( a ^e , m r ) +

e,m      e,m где C , и D ,  – произвольные на начальном

+

( a ^e , m ) 2

n

-

Jn

+

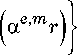
1 '

e , m

этапе постановки присоединенной краевой задачи амплитудные коэффициенты, на которые в дальнейшем будут наложены условия, обеспечивающие удовлетворение решения (50) уравнению (48); p e ’ m ( a ^e ’ m r ) — частные решения неоднородного дифференциального уравнения:

+

+

9      2

(" em Г — 7

+ - p

p

r

e , m

1            f 9

R ( r ) + - R ( r ) + a²

^^^^^^B

r

^-" R ( r ) = J - ( a r ) , (51)

2 ^

то есть

p '' e , m + - p ' e , m +	"          9        2 " ( a e , m ) - ^	p e , m =
r	\       / r	(52)

= D^e , ^mJ_- ( a ^e , m r ) .

( a ^e , m r )

-

+

- D^e , ^mJ_- (a⁶ , m r ) = A^e , ^mJ_- (a⁶ , m r ) .

Из (55) видно, что решения (50) с учетом уравнений (52), (53) удовлетворяют присоединенным уравнениям Гельмгольца (48), соответствующим краевым задачам Дирихле и Неймана о возбуждении несобственных (присоединенных к источнику) волн типа Е и Н распределенным источником в виде бегущей волны при условии:

D e , m _— D e , m _ д в , m

В том случае, когда

D e , m _ D e , m

, , _x Y_n ( a ^mr ) J_n ( a ^mr ) ,     .

J „ (a ^mr J ' /—\ ' a (a ^mr) n ⁽     ) W a ^mr ⁽     )

решения (50) удовлетворяют обычному (однородному) уравнению Гельмгольца.

Граничные условия (49) приводят к уравнениям:

a r                   I .

⁺ 2 Y n ( ^{a r} ) l ^J n ( ^{a r} )

Ce — iz. De J Jn (a ^ ) + P e (a ^ ) = 0(58)

для Е-волн и

Cm — izDm J Jn (a ma) + p'm (“ ma ) = 0(59)

для Н-волн.

Поскольку поперечные волновые числа Е-волн удовлетворяют уравнению:

Jn (aea) _ 0 ,(60)

равенство (58) выполняется тождественно. При этом в (54) полагаем:

x

—

n ²

( a ^mr ) 2

+

[ J n (a- r m.

Функция (64) обеспечит, если значения am находятся из уравнения (61), выполнение равенства (62) только при условии

1 —_ 0. (a ^mr )²

R (ar)_ Jn (aer), что обеспечивает обращение в нуль подынтегральное выражения при r _ a. Поскольку поперечные волновые числа Н-волн удовлетворяют

уравнению:

Jn (ama)_ 0,(61)

для выполнения равенства (59) необходимо, чтобы p'm (ama) _ 0 .(62)

Положив в (54) R ( a r ) _ J n ( a ^mr ) , имеем:

p' ^m ( a ^mr ) _

, ,     - Yn (amr) Jn (amr) ,.

_— J _n (a ^mr J '----}----e-----a (a ^mr ) + (63)

nV ’       W (amr)

. / „ x , Jn (a m r ) , „ x

+ Y„ amr J         a amr , n (    ) W (amr) ()

Выражение (63) приводим к виду:

p' ^m ( a ^mr ) _

- Yn (amr)Jn(amr) ,.

_ — J _n (a ^mr J '---/—' a (a ^mr +

n(    )       W (amr)       ()

( a ^m r )

+ ' 2    [ ^J n ( ^a r ) ^{— J} n — i ( ^a r ) x

То есть, граничное условие на экранирующей поверхности в задаче Неймана на присоединенном уравнении Гельмгольца требует выполнения равенства (65). Итак, показано, что функции (50) при выполнении условия (56) удовлетворяют присоединенным уравнениям Гельмгольца (48). При выполнении условия (57) они удовлетворяют однородным уравнениям Гельмгольца. Для того, чтобы эти функции были решениями краевых задач Дирихле и Неймана необходимо удовлетворение граничных условий (49) на экранирующей поверхности. При этом значения a ^e и a ^m определяются как корни уравнений (60) и (61).

Рассмотренные задачи фактически являются задачами возбуждения волн в экранированном волноводе источником типа антенны бегущей волны, которые в данном случае являются несобственными, «присоединенными» к источнику волнами, не существующими без источника. По-

скольку «присоединенные» волны находятся в синхронизме с возбуждающей их бегущей волной и указанные волны являются энергетически связанными, рассмотренную задачу следует называть самосогласованной. Таким образом, для направляющих структур наряду с обычными краевыми задачами о собственных волнах могут быть сформулированы задачи о волнах на присоединенном уравнении Гельмгольца, которые имеют линейную зависимость поля от продольной координаты за счет распределенного отбора мощности от волны возбуждения

x J n + 1 ( a ^mr ) ] Y n ( a m r ) _

Заключение

Расширено понятие самосогласованных краевых задач в теории электромагнетизма. Сформу-

лированы наиболее распространенные подходы, приводящие к самосогласованным задачам, основывающиеся на образовании замкнутых циклов: искомое решение вычисляется через функцию первичного источника и подставляется в граничные условия, соответствующие однородной краевой задаче. В результате последняя сводится либо к системе однородных интегральных уравнений, либо к дифференциальным уравнениям с правой частью, представляющей собой решение однородной краевой задачи – задачи на соответствующем однородном дифференциальном уравнении.

Работа выполнена при финансовой поддержке Российского научного фонда, грант № 17-1901628.