Формулы для младших тейлоровских коэффициентов однородных поверхностей
Автор: Суковых Валерий Игоревич
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика труды III международной конференции "Геометрический анализ и его приложения"
Статья в выпуске: 5 (36), 2016 года.
Бесплатный доступ
В статье развивается коэффициентный подход к задаче описания голоморфно-однородных вещественных гиперповерхностей 3-мерного комплексного пространства. В модельной ситуации поверхностей общего положения совокупность из 100 параметров, определяющих однородные строго псевдо-выпуклые многообразия, сводится к 7 тейлоровским коэффициентам нормального уравнения Мозера. Описываются промежуточные формулы для коэффициентов и параметров векторных полей, касательных к обсуждаемым однородным многообразиям. Строится система полиномиальных уравнений на итоговую группу параметров. Получена оценка количества однородных поверхностей изучаемого класса. Все необходимые сложные вычисления реализуются в пакете символьной математики Maple.
Голоморфное преобразование, ряд тейлора, вещественная гиперповерхность, алгебра ли, нормальная форма уравнения, система полиномиальных уравнений, символьные вычисления
Короткий адрес: https://sciup.org/14968849
IDR: 14968849 | DOI: 10.15688/jvolsu1.2016.5.10
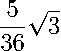
Список литературы Формулы для младших тейлоровских коэффициентов однородных поверхностей
- Арапов, В.С. О вещественных тейлоровских коэффициентах однородных гиперповерхностей пространства C3/В.С. Арапов, А.В. Лобода//Материалы 12-й международной летней школы-конференции. -Казань: Изд-во Казан. мат. о-ва, 2015. -C. 34-35.
- Кружилин, Н.Г. Аффинная и голоморфная эквивалентность трубчатых областей в C2/Н.Г. Кружилин, П.А. Солдаткин//Мат. заметки. -2004. -Т. 75, вып. 5. -C. 670-682.
- Лобода, А.В. Использование компьютерных алгоритмов в задаче коэффициентного описания однородных поверхностей/А.В. Лобода, В.И. Суковых//Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2015. № 1. С. 14-22.
- Лобода, А.В. Локальное описание однородных вещественных гиперповерхностей двумерного комплексного пространства в терминах их нормальных уравнений/А.В. Лобода//Функцион. анализ. -2000. -Т. 34, вып. 2. -C. 33-42.
- Лобода, А.В. О тейлоровских коэффициентах голоморфно-однородных поверхностей общего положения/А.В. Лобода, В.И. Суковых//Тез. докл. Воронеж. зим. мат. шк. -Воронеж: Изд-во ВГУ, 2015. -C. 72-73.
- Лобода, А.В. Об опорных наборах коэффициентов для голоморфно-однородных СПВ-гиперповерхностей в C3/А.В. Лобода, В.И. Суковых//Геометрический анализ и его приложения: материалы 3-й Междунар. шк.-конф. -Волгоград: Изд-во ВолГУ, 2016. -C. 133-138.
- Лобода, А.В. Об определении однородной строго псевдо-выпуклой гиперповерхности по коэффициентам ее нормального уравнения/А.В. Лобода//Мат. заметки. -2003. -Т. 73, № 3. -C. 419-423.
- Лобода, А.В. Однородные строго псевдо-выпуклые гиперповерхности в C3 с двумерными группами изотропии/А.В. Лобода//Мат. сб. -2001. -Т. 192. -C. 3-24.
- Applications of differential algebra for computing Lie algebras of infinitesimal CRautomorphisms/M. Sabzevari, A. Hashemi, B.␣M. Alizadeh, J. Merker//Electronic text data. -Mode of access: http://arxiv.org/abs/1212.3070. -Title from screen.
- Beloshapka, V.K. Homogeneous hypersurfaces in C3, associated with a model CR-cubic/V.K. Beloshapka, I.G. Kossovskiy//J. Geom. Anal. -2010. -Vol. 20, № 3. -P. 538-564.
- Cartan, E. Sur la geometrie pseudoconforme des hypersurfaces de deux variables complexes/E. Cartan//Ann. Math. Pura Appl. -1932. -Vol. 11, № 4. -P. 17-90.
- Chern, S.S. Real hypersurfaces in complex manifolds/S.S. Chern, J.K. Moser//Acta Math. -1974. -Vol. 133, № 3. -P. 219-271.
- Eastwood, M. On affine normal forms and a classification of homogeneous surfaces in affine three-space/M. Eastwood, V.V. Ezhov//Geom. Dedicata. -1999. -Vol. 77. -P. 11-69.
- Fels, G. On affine normal forms and a classification of homogeneous surfaces in affine three-space/G. Fels, W. Kaup//Acta Math. -2008. -Vol. 210. -P. 1-82.
- Isaev, A.V. On the number of affine equivalence classes of spherical tube hypersurfaces/A.V. Isaev, W. Kaup//Math. Ann. -2011. -Vol. 349. -P. 59-74.
