Формулы для вычисления универсальных коэффициентов при принятии многокритериальных решений
Автор: Пиявский С.А.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Методы и технологии принятия решений
Статья в выпуске: 2 (32) т.9, 2019 года.
Бесплатный доступ
Проблема многокритериального выбора является ключевым элементом принятия сложных решений. Предложен ряд методов, позволяющих предполагать, что принимаемые с их использованием решения наиболее рациональны. Их основным элементом является линейная свёртка частных критериев, а различие состоит в тех или иных эвристических или экспертных способах задания числовых коэффициентов сравнительной важности критериев. Ранее автором был разработан подход, который позволяет применять при формировании линейной свёртки заранее рассчитанные универсальные таблицы числовых коэффициентов важности частных критериев. Для расчёта использовался преимущественно метод Монте-Карло, что при большом числе критериев создавало значительные вычислительные трудности из-за недостаточной точности датчика случайных чисел и лавинообразного увеличения объёма вычислений. В настоящей статье получены формулы для расчёта универсальных коэффициентов важности. Они основаны на нумерологическом подходе, обобщающем закономерности, которые проявились при анализе рассчитанных статистическим методом таблиц универсальных коэффициентов. Полученные формулы позволяют использовать универсальные коэффициенты важности критериев в задачах с любым количеством критериев без специального программного обеспечения.
Принятие решений, многокритериальный выбор, универсальные коэффициенты важности критериев, нумерологический подход
Короткий адрес: https://sciup.org/170178824
IDR: 170178824 | УДК: 519.5 | DOI: 10.18287/2223-9537-2019-9-2-282-298
Текст научной статьи Формулы для вычисления универсальных коэффициентов при принятии многокритериальных решений
В методах принятии решений на основе многокритериальной модели (например, [1-10]) присутствуют два момента: объективный и субъективный. Объективный момент связан с адекватностью полноты и точности описания сущности решаемой проблемы – и здесь привлечение лицом, принимающим решение (ЛПР), различных экспертов в качестве источников достоверной информации следует только приветствовать, тем более что в этой функции ЛПР не может их заменить собой. Субъективный момент связан с сопоставлением частных критериев по их сравнительной важности в аспекте целостной ситуации, в рамках которой принимается решение. В этой функции ЛПР никто и никакой коллектив не может заменить, т.к. ответственность за последствия принятого решения несёт ЛПР. Поэтому важно, в каком виде тот или иной метод предусматривает формализованное выражение этой воли ЛПР.
В большинстве методов поддержки принятия решения предлагается облечь эту волю в форму числовых коэффициентов ai сравнительной важности n частных критериев [1-4]:
a i > 0, i = 1, ‘ y n a = 1.
n ;
I Д-и = 1 i
Это позволяет свести определение наиболее рационального решения у * из множества допустимых решений Y к оптимизации на этом множестве скалярного критерия F (т.н. комплексного критерия, свёртки критериев) как некоторой функции от частных критериев f ( у ), г = 1,..., n , у е Y , «взвешенных» своими коэффициентами важности:
F ( у ) = F( a i f 1 ( у ), а 2 f 2 ( У ),..., a n f n ( У ))
Если считать для определенности, что желательно минимизировать значения каждого частного критерия, то после задания коэффициентов (1) наиболее рациональное решение у определяется строго формальным путём:
*
F ( у ) = min F ( a f ( у X a f ( у Х-, a fn ( у )) y е Y 1
при заданном значении вектора ( a 1, a 2,..., a n ) . Однако, в этом субъективном моменте и таится основное препятствие к широкому применению на практике подобным образом формализованных методов поддержки принятия решений.
ЛПР - как отдельное лицо, так и выступающая в этом качестве небольшая группа лиц -хорошо понимает условность и неопределённость назначаемых коэффициентов (1), поскольку никакой человек не в состоянии облечь свои неформализованные предпочтения в столь точную числовую форму, и потому не доверяет полученному результату. Борясь с сомнениями, ЛПР может привлекать экспертов и формирует числовые значения коэффициентов важности критериев примерно по такому алгоритму: если 30% экспертов сказали, что второй критерий важнее первого, а остальные 70% сказали обратное, то коэффициенты важности критериев могут быть приняты соответственно 0,3 и 0,7.
В ряде методов (см., например, [8-10]) ЛПР предлагается произвести попарное сравнение критериев по важности, используя порядковую шкалу . На основе той или иной достаточно разумной гипотезы результаты переводятся в форму числовых коэффициентов. Но при этом сомнения переносятся на саму гипотезу. Например, известный ряд {3, 5, 7, 9} в методе анализа иерархии Т. Саати [8-10] из-за необходимости произвести множественные сравнения становится труднореализуемым на практике.
-
1 Постановка задачи
Начиная с работ [11-13] и, в особенности, в [14-16], а также в настоящей статье, последовательно развивается иной подход к субъективному моменту в принятии многокритериальных решений. Он состоит в том, что ЛПР должен формализовать свои предпочтения в отношении частных критериев оптимальности не в виде числовых коэффициентов или парных сравнений, а в виде политики выбора , распределив частные критерии по нескольким группам важности .
Пронумеруем группы важности по возрастанию важности входящих в них критериев индексом р, где р = 1,..., N < n. Обозначим через 1р множество индексов критериев, входящих в р-ю группу важности. Имеем ир=11 р =с.--n};
] I р #0 , р = 1,П, N ; 1
I р n I v =0 , р = 1,П , N .
Тогда, с формальной точки зрения, политика выбора задаётся ЛПР функцией р(i), i = 1,...,n, однозначно сопоставляющей номеру каждого частного критерия отвечающий ему номер некоторой группы важности. Это добавляет к условиям (1) следующие ограничения на значения коэффициентов важности критериев:
a i > a j V i * j , р ( i ) > X j ), i , j e {1,..., n } .
Соотношения (1), (3) определяют некоторую область X значений вектора коэффициентов важности критериев a = (a1,a2,...an). Каждый вектор из этой области удовлетворяет пред почтениям ЛПР (3) и потому с равным основанием должен быть учтён при формировании вектора коэффициентов важности a = (a1,a2,...an), который используется в функции (2) для определения оптимального решения у*.
В настоящее время в практике принятия решений в таких случаях комплексного учёта однородной по значимости информации используются два естественных подхода: усредняющий (принцип Лапласа) и гарантирующий (принцип максимина, Вальда и Ю.Б. Гермейера). В [14, 15] показано, что в обоих случаях комплексный вектор коэффициентов важности критериев не зависит от конкретной решаемой задачи принятия решения, а зависит лишь от того, как частные критерии распределены по группам важности в соответствии с (3).
При гарантирующем подходе для расчёта комплексного вектора коэффициентов важности критериев a в [16] получены соответствующие формулы. При усредняющем подходе в [14] показано, что компоненты вектора a можно определять по формуле
∫ αi dα
at = ^Х , i = 1,..., n,
∫ dα
α∈X т.е. геометрически компоненты вектора a представляют собой координаты центра масс области Х. Это позволяет вычислять коэффициенты (4) для небольшого числа критериев геометрическим путём, непосредственно вычисляя многомерные интегралы, а в общем случае -вычислять (4) приближённо методом статистических испытаний или прямым перебором с малым шагом. В [15] разработан метод масок, позволяющий приближённо вычислять (4), исключив метод статистических испытаний.
Однако следует признать, что при значительном числе критериев все эти методы порождают значительные вычислительные сложности, что создаёт определённые препятствия в реализации указанных методов в информационных системах поддержки принятия решений.
-
2 Формулы для расчёта задающих коэффициентов
В качестве исходной базы для разработки аналитических методов расчёта универсальных коэффициентов важности критериев в свёртке Лапласа используется предложенный в [15] нумерологический подход. Суть его заключается в том, чтобы, используя результаты, полученные для небольшого количества критериев (от 2 до 10), попытаться «угадать» аналитическое выражение, позволяющее получить результаты, совпадающие с базовыми, а затем использовать эти выражения уже в строгих математических рассуждениях.
Здесь за базу приняты результаты, представленные в таблицах 1-3, и показано их последовательное использование.
В таблице 1 приведены значения для расчёта универсальных коэффициентов важности критериев в свёртке Лапласа, полученные из строгих геометрических построений для числа критериев от 2 до 4. Значения в каждой строке таблицы 1 приведены к одному общему знаменателю.
Таблица 1 - Значения для расчёта универсальных коэффициентов важности критериев в свёртке Лапласа
|
Количество частных критериев в задаче принятия решений |
Количество критериев в каждой группе важности |
Универсальные значения коэффициентов важности критериев |
||||||
|
Группа важности критериев |
Группа важности критериев |
|||||||
|
В1 |
В2 |
В3 |
В4 |
В1 |
В2 |
В3 |
В4 |
|
|
2 |
2 |
1/2 |
||||||
|
1 |
1 |
1/4 |
3/4 |
|||||
|
3 |
3 |
1/3 |
||||||
|
2 |
1 |
7/36 |
22/36 |
|||||
|
1 |
2 |
4/36 |
16/36 |
|||||
|
1 |
1 |
1 |
4/36 |
10/36 |
22/36 |
|||
|
4 |
4 |
12/48 |
||||||
|
3 |
1 |
8/48 |
25/48 |
|||||
|
2 |
2 |
5/48 |
19/48 |
|||||
|
1 |
3 |
3/48 |
15/48 |
|||||
|
2 |
1 |
1 |
5/48 |
13/48 |
25/48 |
|||
|
1 |
2 |
1 |
3/48 |
10/48 |
25/48 |
|||
|
1 |
1 |
2 |
3/48 |
7/48 |
19/48 |
|||
|
1 |
1 |
1 |
1 |
3/48 |
7/48 |
13/48 |
25/48 |
|
Для большего числа критериев геометрический подход применить не удалось, и потому был использован статистический подход, позволивший приближенно рассчитать таблицы универсальных коэффициентов важности для количества критериев от 5 до 10. При большем числе критериев возрастает погрешность, вызванная несовершенством датчиков случайных чисел и недостаточным числом случайных испытаний. Однако десяти критериев вполне достаточно для проверки результатов, полученных с помощью нумерологической гипотезы.
В таблице 2 представлен фрагмент таблицы 1 для политик выбора, в которых в каждую группу важности входит лишь по одному критерию. Универсальные коэффициенты важности критериев в таких политиках выбора названы задающими коэффициентами. Можно заметить, что числа в правой части таблицы 2 ( задающие коэффициенты) подчиняются определённой закономерности.
-
1) общий знаменатель вычисляется по формуле n 2( n - 1);
-
2) числитель в первом столбце равен n - 1;
-
3) числители остальных коэффициентов в строке, кроме последнего ненулевого, равны числителям коэффициентов, стоящих в таблице 2 непосредственно над ними плюс 2;
-
4) числитель последнего ненулевого коэффициента в строке равен разности n 2( n - 1) и суммы числителей всех остальных чисел в строке.
Таблица 2- Таблица задающих коэффициентов (фрагмент таблицы 1)
|
Количество частных критериев |
Количество критериев в каждой группе важности |
Универсальные значения коэффициентов важности критериев |
||||||
|
Группа важности критериев |
Группа важности критериев |
|||||||
|
В1 |
В2 |
В3 |
В4 |
В1 |
В2 |
В3 |
В4 |
|
|
2 |
1 |
1 |
1/4 |
3/4 |
||||
|
3 |
1 |
1 |
1 |
2/18 |
5/18 |
11/18 |
||
|
4 |
1 |
1 |
1 |
1 |
3/48 |
7/48 |
13/48 |
25/48 |
Используя эту нумерологическую гипотезу, можно последовательно построить аналогичные таблицы задающих коэффициентов для любого количества критериев. В таблицах 3 и 4 показаны задающие коэффициенты для количеств критериев от 2 до 10. Их сравнение с аналогичными результатами, рассчитанными статистическим подходом, подтвердили достоверность этой нумерологической гипотезы и дают основания распространить её на любое число критериев. Относительное отклонение этих значений от полученных статистическим методом не превышает нескольких процентов и связано с ограниченным числом испытаний в статистическом методе и несовершенством датчика случайных чисел.
Таблица 3 – Числитель и знаменатель формулы для расчёта задающих коэффициентов
|
Количество критериев |
Знаменатель формулы |
Числитель формулы |
|||||||||
|
Группа важности критерия |
|||||||||||
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
В8 |
В9 |
В10 |
||
|
2 |
4 |
1 |
3 |
||||||||
|
3 |
18 |
2 |
5 |
11 |
|||||||
|
4 |
48 |
3 |
7 |
13 |
25 |
||||||
|
5 |
100 |
4 |
9 |
15 |
27 |
45 |
|||||
|
6 |
180 |
5 |
11 |
17 |
29 |
47 |
71 |
||||
|
7 |
294 |
6 |
13 |
19 |
31 |
49 |
73 |
103 |
|||
|
8 |
448 |
7 |
15 |
21 |
33 |
51 |
75 |
105 |
141 |
||
|
9 |
648 |
8 |
17 |
23 |
35 |
53 |
77 |
107 |
143 |
185 |
|
|
10 |
900 |
9 |
19 |
25 |
37 |
55 |
79 |
109 |
145 |
187 |
235 |
Таблица 4 – Задающие коэффициенты (расчёт по предложенным формулам)
|
Количество критериев |
Числитель формулы |
|||||||||
|
Группа важности критерия |
||||||||||
|
В1 |
В2 |
В3 |
В4 |
В5 |
В6 |
В7 |
В8 |
В9 |
В10 |
|
|
2 |
0,2500 |
0,7500 |
||||||||
|
3 |
0,1111 |
0,2778 |
0,6111 |
|||||||
|
4 |
0,0625 |
0,1458 |
0,2708 |
0,5208 |
||||||
|
5 |
0,0400 |
0,0900 |
0,1500 |
0,2700 |
0,4500 |
|||||
|
6 |
0,0278 |
0,0611 |
0,0944 |
0,1611 |
0,2611 |
0,3944 |
||||
|
7 |
0,0204 |
0,0442 |
0,0646 |
0,1054 |
0,1667 |
0,2483 |
0,3503 |
|||
|
8 |
0,0156 |
0,0335 |
0,0469 |
0,0737 |
0,1138 |
0,1674 |
0,2344 |
0,3147 |
||
|
9 |
0,0123 |
0,0262 |
0,0355 |
0,0540 |
0,0818 |
0,1188 |
0,1651 |
0,2207 |
0,2855 |
|
|
10 |
0,0100 |
0,0211 |
0,0278 |
0,0411 |
0,0611 |
0,0878 |
0,1211 |
0,1611 |
0,2078 |
0,2611 |
На основе этого в [15] предложен алгоритм вычисления универсальных коэффициентов важности критериев для любого числа критериев. Для этого используются задающие коэффициенты и так называемая « маска » рассчитываемой универсальной таблицы. Однако подобный путь построения таблиц при большем числе критериев очень трудоёмок.
Формулу для вычисления задающих коэффициентов из таблицы 4 можно представить в виде:
a
ns
1 / n 2 при s = 1,
= < Cs + 2 n - 1
n 2 ( n - 1 )
при 1 < s < n,
где s - группа важности, a ns – универсальные коэффициенты важности в политике выбора для n критериев, в которой каждая группа важности включает ровно один критерий. Задающий параметр C s принимает значения, указанные в таблице 5.
Таблица 5 – Значения задающего параметра C s
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Cs |
нет |
0 |
6 |
18 |
36 |
60 |
90 |
126 |
168 |
216 |
Формула для вычисления значения задающего параметра из таблицы 5 имеет вид:
C s = 3( s - 1)( s - 2) при s > 1.
Окончательно имеем
a ns
1 / n 2 при s = 1, 3( s - 1)( s - 2) + 2 n - 1
n 2 ( n - 1 )
при 1 < s < n.
Например, в частном случае n = 2, s = 2 получаем a22
3 X 1 x 0 + 4 -1 _ 3 4 x 1 = 4.
Эта формула даёт те же результаты, что приведены в таблицах 1-4.
Важность формулы (5) стоит в том, что согласно нумерологической гипотезе она может быть распространена на любое число критериев и групп важности, хотя получена на экспериментальной основе для числа критериев от 2 до 10 и соответствующих этому количеству групп важности.
Поскольку можно разработать алгоритм последовательного построения масок таблиц универсальных коэффициентов важности для любого числа критериев, возникла возможность отказаться от приближённого статистического метода расчёта универсальных таблиц и строить эти таблицы по точному алгоритму. Кроме того, существенно уменьшаются требования к объёму памяти БД универсальных коэффициентов важности, поскольку можно хранить не сами таблицы, а их маски.
-
3 Формулы для расчета универсальных коэффициентов важности «крайних по важности» критериев
Вычислим универсальный коэффициент a nk при критериях из группы наиболее важных критериев (крайние справа для политики выбора - цепочке 1,…, 1, k ). Здесь n - общее количество критериев, а k - количество критериев в цепочке, входящих в группу самых важных, так что единиц в этой цепочке n - k . Исходя из того, что сумма коэффициентов всех критериев в цепочке с учётом (5) равна 1, получим
n - 1
n ( n - 1)
a nk =------------
-E
n-k 3( s —1)( s — 2) + 2 n — 1
1 s = 2
n 2( n - 1) k
.
В цепочке, где первые n - k элементов равны 1, их коэффициенты вычитаются из 1, а затем результат делится на количество самых важных критериев.
С учётом (6)
1 ^i
= “ + Z n
= n - k
S nk / - 5 = i a ns
n - k 3( s - 1)( s - 2) + 2 n - 1
s = 2 n 2( n - 1)
=-1+-г-1— (3 y n - k s 2 - 9 у n - k s +y n - k (6 + 2 n - 1)). n 2 n 2( n - 1) — s = 2 — s = 2 — s = 2
По известным формулам суммирования рядов (см., например, [17])
У q . 1 s = 2 ( q +»
- q . , s 2 = q (2 q 2 + 3 q + 1).
Тогда
V n - k n - k
4 1 = — s = 2 s = 2 ( n - k + 1) - 1
q 2 -’-2 s 2 = n J(2( n - k ) 2 + 3( n - k ) + 1) - 1.
s 2 6
Соответственно
S nk = 4 (1 + (3 q 2 - 9 q 1 + (2 n + 5)( n - k - 1)))).
n 2 ( n - 1)
Например, в частном случае n = 2, k = 2 получаем q, = 1 х 2 -1 = 0, q2 = 1(2 + 3 +1) -1 = 0, S21 = 1(1 + 9 x 0) = 1.
1 2 2 6 21 4 4
Чтобы получить a n k - значение универсального коэффициента важности критерия (верхний индекс обозначает right ) для самых важных k критериев из общего числа критериев n -нужно вычесть Snk из единицы и поделить результат на k :
. r -1 - S nk ank = ,
.
k
Далее можно найти alnk - значение универсального коэффициента важности критерия (верхний индекс обозначает left ) для наименее важных p критериев из общего числа критериев n . Для этого следует рассмотреть цепочку p , ( n - p ). Поскольку сумма универсальных коэффициентов всех критериев равна единице, то
i _1- ( n - p ) a nk a nk =
p
В качестве примера в таблице 6 приведены результаты расчётов по формулам (7), (8) для шести критериев.
Таблица 6 - «Крайние по важности» (правый и левый) универсальные коэффициенты важности шести критериев
|
Количество наиболее ( k ) или наименее ( p ) важных критериев |
q 1 |
q 2 |
S |
r a nk |
a nk |
|
1 |
14 |
54 |
0,606 |
0,394 |
0,028 |
|
2 |
9 |
29 |
0,344 |
0,328 |
0,044 |
|
3 |
5 |
13 |
0,183 |
0,272 |
0,061 |
|
4 |
2 |
4 |
0,089 |
0,228 |
0,086 |
|
5 |
0 |
0 |
0,028 |
0,194 |
0,121 |
-
4 Таблицы универсальных коэффициентов важности критериев при принятии решений с двумя группами важности
В практических задачах используется ограниченное количество групп важности, чаще всего не более трёх. Используя формулы (7), (8), легко рассчитать точное значение универсальных коэффициентов важности критериев в любых задачах принятия решений, в которых используются не более трёх групп важности критериев. Так, в таблице 7 приведены значения универсальных коэффициентов важности критериев для двух групп важности при общем числе критериев от 2 до 10.
На основе таблицы 7 на рисунке 1 показаны суммарные значения универсальных коэффициентов важности критериев, относящихся к одинаковой группе важности, в зависимости от относительного количества критериев соответствующей группы важности в общем количестве критериев.
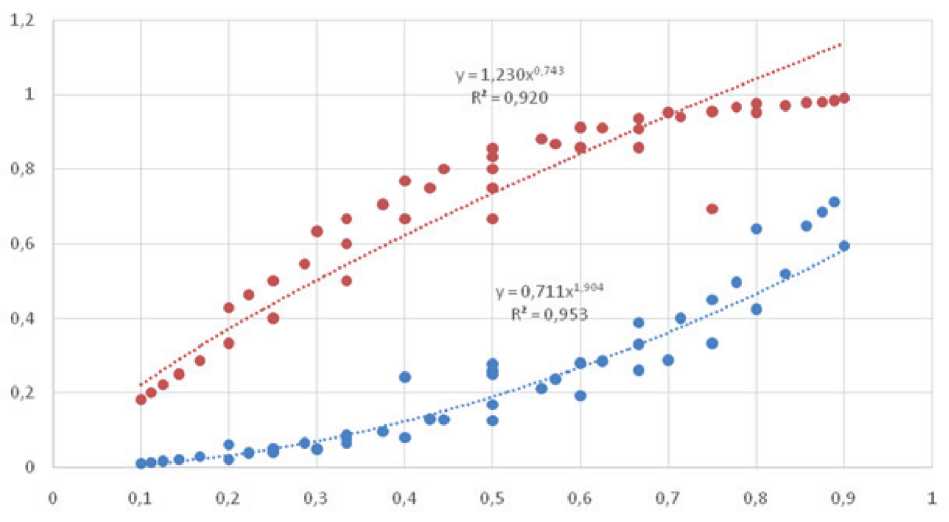
Рисунок 1 - К приближённому вычислению универсальных коэффициентов важности критериев при двух группах важности
Видно, что с приемлемой погрешностью можно использовать вместо таблицы 7 или более громоздких формул (7), (8) простые приближённые формулы:
r a nk
a
l np
0,74
1,231 [ к । к < n )
0,712 Гp А ,9 p у n )
(квадрат коэффициента корреляции Пирсона R 2 =0,92).
(квадрат коэффициента корреляции Пирсона R 2=0,95),
где к и p - количество критериев соответственно б о льшей и меньшей важности.
Таблица 7 - Универсальные коэффициенты важности критериев в задачах принятия решений с двумя группами важности
|
Общее количество критериев |
Распределение критериев по группам важности |
Универсальные коэффициенты важности критериев в свёртке Лапласа F = У", a fi ^ min i = 1 wi |
Универсальные коэффициенты важности критериев в свёртке Гермейера F = max a i f i ^ min i = 1,..., n (по [16]) |
|||
|
(по |
[14]) |
|||||
|
n |
B1 |
B2 |
B1 |
B2 |
B1 |
B2 |
|
2 |
1 |
1 |
0,250 |
0,750 |
0,333 |
0,667 |
|
3 |
1 |
2 |
0,111 |
0,444 |
0,143 |
0,429 |
|
3 |
2 |
1 |
0,194 |
0,611 |
0,250 |
0,500 |
|
4 |
1 |
3 |
0,063 |
0,313 |
0,077 |
0,308 |
|
4 |
2 |
2 |
0,104 |
0,396 |
0,125 |
0,375 |
|
4 |
3 |
1 |
0,160 |
0,521 |
0,200 |
0,400 |
|
5 |
1 |
4 |
0,040 |
0,240 |
0,048 |
0,238 |
|
5 |
2 |
3 |
0,065 |
0,290 |
0,071 |
0,286 |
|
5 |
3 |
2 |
0,093 |
0,360 |
0,111 |
0,333 |
|
5 |
4 |
1 |
0,138 |
0,450 |
0,167 |
0,333 |
|
6 |
1 |
5 |
0,028 |
0,194 |
0,032 |
0,194 |
|
6 |
2 |
4 |
0,044 |
0,228 |
0,045 |
0,227 |
|
6 |
3 |
3 |
0,061 |
0,272 |
0,067 |
0,267 |
|
6 |
4 |
2 |
0,086 |
0,328 |
0,100 |
0,300 |
|
6 |
5 |
1 |
0,121 |
0,394 |
0,143 |
0,286 |
|
7 |
1 |
6 |
0,020 |
0,163 |
0,023 |
0,163 |
|
7 |
2 |
5 |
0,032 |
0,187 |
0,031 |
0,188 |
|
7 |
3 |
4 |
0,043 |
0,218 |
0,043 |
0,217 |
|
7 |
4 |
3 |
0,059 |
0,255 |
0,063 |
0,25 |
|
7 |
5 |
2 |
0,080 |
0,299 |
0,091 |
0,273 |
|
7 |
6 |
1 |
0,108 |
0,350 |
0,125 |
0,250 |
|
8 |
1 |
7 |
0,016 |
0,141 |
0,018 |
0,140 |
|
8 |
2 |
6 |
0,025 |
0,158 |
0,023 |
0,159 |
|
8 |
3 |
5 |
0,032 |
0,181 |
0,030 |
0,182 |
|
8 |
4 |
4 |
0,042 |
0,208 |
0,042 |
0,208 |
|
8 |
5 |
3 |
0,057 |
0,239 |
0,059 |
0,235 |
|
8 |
6 |
2 |
0,075 |
0,275 |
0,083 |
0,250 |
|
8 |
7 |
1 |
0,098 |
0,315 |
0,111 |
0,222 |
|
9 |
1 |
8 |
0,012 |
0,123 |
0,014 |
0,123 |
|
9 |
2 |
7 |
0,019 |
0,137 |
0,017 |
0,138 |
|
9 |
3 |
6 |
0,025 |
0,154 |
0,022 |
0,156 |
|
9 |
4 |
5 |
0,032 |
0,174 |
0,029 |
0,176 |
|
9 |
5 |
4 |
0,042 |
0,198 |
0,040 |
0,200 |
|
9 |
6 |
3 |
0,055 |
0,224 |
0,056 |
0,222 |
|
9 |
7 |
2 |
0,071 |
0,253 |
0,077 |
0,231 |
|
9 |
8 |
1 |
0,089 |
0,285 |
0,100 |
0,200 |
|
10 |
1 |
9 |
0,010 |
0,110 |
0,011 |
0,110 |
|
10 |
2 |
8 |
0,016 |
0,121 |
0,014 |
0,122 |
|
10 |
3 |
7 |
0,020 |
0,134 |
0,017 |
0,136 |
|
10 |
4 |
6 |
0,025 |
0,150 |
0,022 |
0,152 |
|
10 |
5 |
5 |
0,032 |
0,168 |
0,029 |
0,171 |
|
10 |
6 |
4 |
0,041 |
0,188 |
0,038 |
0,192 |
|
10 |
7 |
3 |
0,053 |
0,210 |
0,053 |
0,211 |
|
10 |
8 |
2 |
0,066 |
0,234 |
0,071 |
0,214 |
|
10 |
9 |
1 |
0,082 |
0,261 |
0,091 |
0,182 |
-
5 Таблицы универсальных коэффициентов важности критериев при принятии решений с тремя группами важности
Используя соотношения (7), (8), легко получить формулу для расчёта универсального коэффициента важности для t критериев средней важности a nmt (верхний индекс обозначает middle ) в задачах принятия решений, в которых, при любом количестве критериев, количество групп важности равно трём:
m ant
1 - Pan p - ka nk
t
В таблице 8 приведены коэффициенты важности критериев при трёх группах важности для количества критериев от 3 до 10.
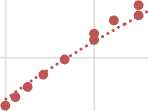
На основе таблицы 8 на рисунке 2 показаны суммарные значения универсальных коэффициентов важности критериев, относящихся к одинаковой группе важности, в зависимости от относительного количества критериев соответствующей группы важности в общем количестве критериев. Видно, что с приемлемой погрешностью можно использовать вместо таблицы 8 или более громоздких формул (7), (8) простые приближённые формулы:
a nk
0,672
1,319 1 k ] k к n )
(квадрат коэффициента корреляции Пирсона R 2 =0,98),
anp
1,789
0,609 1 p । P к n )
(квадрат коэффициента корреляции Пирсона R 2 =0,99),
где k , t , p – количество членов групп критериев по убыванию важности соответственно.
Таблица 8 - Универсальные коэффициенты важности критериев в задачах принятия решений с тремя группами важности (начало)
|
Общее количество критериев |
Распределение критериев по группам важности |
Универсальные коэффициенты важности критериев в свёртке Лапласа F = a fi ^ min ^i = 1 ij i (по [14]) |
Универсальные коэффициенты важности критериев в свёртке Гермейера F = max a i f i ^ min i = 1,..., n (по [16]) |
||||||
|
n |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
|
3 |
1 |
1 |
1 |
0,111 |
0,278 |
0,611 |
0,182 |
0,273 |
0,545 |
|
4 |
2 |
1 |
1 |
0,104 |
0,271 |
0,521 |
0,154 |
0,231 |
0,462 |
|
4 |
1 |
2 |
1 |
0,063 |
0,208 |
0,521 |
0,111 |
0,222 |
0,444 |
|
4 |
1 |
1 |
2 |
0,063 |
0,146 |
0,396 |
0,097 |
0,129 |
0,387 |
|
5 |
3 |
1 |
1 |
0,093 |
0,270 |
0,450 |
0,133 |
0,200 |
0,400 |
|
5 |
2 |
2 |
1 |
0,065 |
0,210 |
0,450 |
0,100 |
0,200 |
0,400 |
|
5 |
1 |
3 |
1 |
0,040 |
0,170 |
0,450 |
0,074 |
0,185 |
0,370 |
|
5 |
2 |
1 |
2 |
0,065 |
0,150 |
0,360 |
0,088 |
0,118 |
0,353 |
|
5 |
1 |
2 |
2 |
0,040 |
0,120 |
0,360 |
0,070 |
0,116 |
0,349 |
|
5 |
1 |
1 |
3 |
0,040 |
0,090 |
0,290 |
0,058 |
0,072 |
0,290 |
|
6 |
4 |
1 |
1 |
0,086 |
0,261 |
0,394 |
0,118 |
0,176 |
0,353 |
|
6 |
3 |
2 |
1 |
0,061 |
0,211 |
0,394 |
0,091 |
0,182 |
0,364 |
|
6 |
2 |
3 |
1 |
0,044 |
0,172 |
0,394 |
0,069 |
0,172 |
0,345 |
|
6 |
1 |
4 |
1 |
0,028 |
0,144 |
0,394 |
0,053 |
0,158 |
0,316 |
|
6 |
3 |
1 |
2 |
0,061 |
0,161 |
0,328 |
0,081 |
0,108 |
0,324 |
|
6 |
2 |
2 |
2 |
0,044 |
0,128 |
0,328 |
0,065 |
0,109 |
0,326 |
|
6 |
1 |
3 |
2 |
0,028 |
0,106 |
0,328 |
0,053 |
0,105 |
0,316 |
|
6 |
2 |
1 |
3 |
0,044 |
0,094 |
0,272 |
0,055 |
0,068 |
0,274 |
Таблица 8 - Универсальные коэффициенты важности критериев в задачах принятия решений с тремя группами важности (продолжение)
|
Общее количество критериев |
Распределение критериев по группам важности |
Универсальные коэффициенты важности критериев в свёртке Лапласа F = V ” , a f ^ min Z—i i = 1 iJ i (по [14]) |
Универсальные коэффициенты важности критериев в свёртке Гермейера F = max a i f i ^ min i = 1,..., ” (по [16]) |
||||||
|
n |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
|
6 |
1 |
2 |
3 |
0,028 |
0,078 |
0,272 |
0,045 |
0,068 |
0,273 |
|
6 |
1 |
1 |
4 |
0,028 |
0,061 |
0,228 |
0,038 |
0,046 |
0,229 |
|
7 |
5 |
1 |
1 |
0,080 |
0,248 |
0,350 |
0,105 |
0,158 |
0,316 |
|
7 |
4 |
2 |
1 |
0,059 |
0,207 |
0,350 |
0,083 |
0,167 |
0,333 |
|
7 |
3 |
3 |
1 |
0,043 |
0,173 |
0,350 |
0,065 |
0,161 |
0,323 |
|
7 |
2 |
4 |
1 |
0,032 |
0,146 |
0,350 |
0,050 |
0,150 |
0,300 |
|
7 |
1 |
5 |
1 |
0,020 |
0,126 |
0,35 |
0,039 |
0,137 |
0,275 |
|
7 |
4 |
1 |
2 |
0,059 |
0,167 |
0,299 |
0,075 |
0,100 |
0,300 |
|
7 |
3 |
2 |
2 |
0,043 |
0,136 |
0,299 |
0,061 |
0,102 |
0,306 |
|
7 |
2 |
3 |
2 |
0,032 |
0,112 |
0,299 |
0,050 |
0,100 |
0,300 |
|
7 |
1 |
4 |
2 |
0,020 |
0,095 |
0,299 |
0,041 |
0,096 |
0,288 |
|
7 |
3 |
1 |
3 |
0,043 |
0,105 |
0,255 |
0,052 |
0,065 |
0,260 |
|
7 |
2 |
2 |
3 |
0,032 |
0,085 |
0,255 |
0,043 |
0,065 |
0,261 |
|
7 |
1 |
3 |
3 |
0,020 |
0,071 |
0,255 |
0,037 |
0,064 |
0,257 |
|
7 |
2 |
1 |
4 |
0,032 |
0,065 |
0,218 |
0,037 |
0,044 |
0,221 |
|
7 |
1 |
2 |
4 |
0,020 |
0,054 |
0,218 |
0,031 |
0,044 |
0,220 |
|
7 |
1 |
1 |
5 |
0,020 |
0,044 |
0,187 |
0,027 |
0,031 |
0,188 |
|
8 |
6 |
1 |
1 |
0,075 |
0,234 |
0,315 |
0,095 |
0,143 |
0,286 |
|
8 |
5 |
2 |
1 |
0,057 |
0,201 |
0,315 |
0,077 |
0,154 |
0,308 |
|
8 |
4 |
3 |
1 |
0,042 |
0,172 |
0,315 |
0,061 |
0,152 |
0,303 |
|
8 |
3 |
4 |
1 |
0,032 |
0,147 |
0,315 |
0,048 |
0,143 |
0,286 |
|
8 |
2 |
5 |
1 |
0,025 |
0,127 |
0,315 |
0,038 |
0,132 |
0,264 |
|
8 |
1 |
6 |
1 |
0,016 |
0,112 |
0,315 |
0,030 |
0,121 |
0,242 |
|
8 |
5 |
1 |
2 |
0,057 |
0,167 |
0,275 |
0,070 |
0,093 |
0,279 |
|
8 |
4 |
2 |
2 |
0,042 |
0,141 |
0,275 |
0,058 |
0,096 |
0,288 |
|
8 |
3 |
3 |
2 |
0,032 |
0,118 |
0,275 |
0,048 |
0,095 |
0,286 |
|
8 |
2 |
4 |
2 |
0,025 |
0,100 |
0,275 |
0,039 |
0,092 |
0,276 |
|
8 |
1 |
5 |
2 |
0,016 |
0,087 |
0,275 |
0,033 |
0,088 |
0,264 |
|
8 |
4 |
1 |
3 |
0,042 |
0,114 |
0,239 |
0,049 |
0,062 |
0,247 |
|
8 |
3 |
2 |
3 |
0,032 |
0,094 |
0,239 |
0,042 |
0,063 |
0,250 |
|
8 |
2 |
3 |
3 |
0,025 |
0,078 |
0,239 |
0,035 |
0,062 |
0,248 |
|
8 |
1 |
4 |
3 |
0,016 |
0,067 |
0,239 |
0,030 |
0,061 |
0,242 |
|
8 |
3 |
1 |
4 |
0,032 |
0,074 |
0,208 |
0,035 |
0,043 |
0,213 |
|
8 |
2 |
2 |
4 |
0,025 |
0,060 |
0,208 |
0,030 |
0,043 |
0,213 |
|
8 |
1 |
3 |
4 |
0,016 |
0,051 |
0,208 |
0,026 |
0,042 |
0,212 |
|
8 |
2 |
1 |
5 |
0,025 |
0,047 |
0,181 |
0,026 |
0,031 |
0,183 |
|
8 |
1 |
2 |
5 |
0,016 |
0,040 |
0,181 |
0,023 |
0,031 |
0,183 |
|
8 |
1 |
1 |
6 |
0,016 |
0,033 |
0,158 |
0,020 |
0,023 |
0,160 |
|
9 |
7 |
1 |
1 |
0,071 |
0,221 |
0,285 |
0,087 |
0,130 |
0,261 |
|
9 |
6 |
2 |
1 |
0,055 |
0,193 |
0,285 |
0,071 |
0,143 |
0,286 |
|
9 |
5 |
3 |
1 |
0,042 |
0,168 |
0,285 |
0,057 |
0,143 |
0,286 |
|
9 |
4 |
4 |
1 |
0,032 |
0,147 |
0,285 |
0,045 |
0,136 |
0,273 |
|
9 |
3 |
5 |
1 |
0,025 |
0,128 |
0,285 |
0,036 |
0,127 |
0,255 |
|
9 |
2 |
6 |
1 |
0,019 |
0,113 |
0,285 |
0,029 |
0,118 |
0,235 |
|
9 |
1 |
7 |
1 |
0,012 |
0,100 |
0,285 |
0,024 |
0,108 |
0,217 |
|
9 |
6 |
1 |
2 |
0,055 |
0,165 |
0,253 |
0,065 |
0,087 |
0,261 |
Таблица 8 - Универсальные коэффициенты важности критериев в задачах принятия решений с тремя группами важности (продолжение)
|
Общее количество критериев |
Распределение критериев по группам важности |
Универсальные коэффициенты важности критериев в свёртке Лапласа F = У ” a f ^ min Z—/ i =1 iJ i (по [14]) |
Универсальные коэффициенты важности критериев в свёртке Гермейера F = max a i f i ^ min i =1,..., ” (по [16]) |
||||||
|
n |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
|
9 |
5 |
2 |
2 |
0,042 |
0,142 |
0,253 |
0,055 |
0,091 |
0,273 |
|
9 |
4 |
3 |
2 |
0,032 |
0,122 |
0,253 |
0,045 |
0,091 |
0,273 |
|
9 |
3 |
4 |
2 |
0,025 |
0,105 |
0,253 |
0,038 |
0,089 |
0,266 |
|
9 |
2 |
5 |
2 |
0,019 |
0,091 |
0,253 |
0,032 |
0,085 |
0,255 |
|
9 |
1 |
6 |
2 |
0,012 |
0,080 |
0,253 |
0,027 |
0,081 |
0,243 |
|
9 |
5 |
1 |
3 |
0,042 |
0,119 |
0,224 |
0,047 |
0,059 |
0,235 |
|
9 |
4 |
2 |
3 |
0,032 |
0,100 |
0,224 |
0,04 |
0,060 |
0,240 |
|
9 |
3 |
3 |
3 |
0,025 |
0,085 |
0,224 |
0,034 |
0,060 |
0,239 |
|
9 |
2 |
4 |
3 |
0,019 |
0,073 |
0,224 |
0,029 |
0,059 |
0,235 |
|
9 |
1 |
5 |
3 |
0,012 |
0,063 |
0,224 |
0,025 |
0,057 |
0,229 |
|
9 |
4 |
1 |
4 |
0,032 |
0,082 |
0,198 |
0,034 |
0,041 |
0,205 |
|
9 |
3 |
2 |
4 |
0,025 |
0,068 |
0,198 |
0,030 |
0,041 |
0,207 |
|
9 |
2 |
3 |
4 |
0,019 |
0,057 |
0,198 |
0,026 |
0,041 |
0,206 |
|
9 |
1 |
4 |
4 |
0,012 |
0,049 |
0,198 |
0,023 |
0,041 |
0,204 |
|
9 |
3 |
1 |
5 |
0,025 |
0,054 |
0,174 |
0,026 |
0,030 |
0,179 |
|
9 |
2 |
2 |
5 |
0,019 |
0,045 |
0,174 |
0,022 |
0,030 |
0,179 |
|
9 |
1 |
3 |
5 |
0,012 |
0,039 |
0,174 |
0,02 |
0,030 |
0,178 |
|
9 |
2 |
1 |
6 |
0,019 |
0,035 |
0,154 |
0,02 |
0,022 |
0,156 |
|
9 |
1 |
2 |
6 |
0,012 |
0,031 |
0,154 |
0,017 |
0,022 |
0,156 |
|
9 |
1 |
1 |
7 |
0,012 |
0,026 |
0,137 |
0,015 |
0,017 |
0,138 |
|
10 |
8 |
1 |
1 |
0,066 |
0,208 |
0,261 |
0,080 |
0,120 |
0,240 |
|
10 |
7 |
2 |
1 |
0,053 |
0,184 |
0,261 |
0,067 |
0,133 |
0,267 |
|
10 |
6 |
3 |
1 |
0,041 |
0,163 |
0,261 |
0,054 |
0,135 |
0,270 |
|
10 |
5 |
4 |
1 |
0,032 |
0,144 |
0,261 |
0,043 |
0,130 |
0,261 |
|
10 |
4 |
5 |
1 |
0,025 |
0,128 |
0,261 |
0,035 |
0,123 |
0,246 |
|
10 |
3 |
6 |
1 |
0,020 |
0,113 |
0,261 |
0,029 |
0,114 |
0,229 |
|
10 |
2 |
7 |
1 |
0,016 |
0,101 |
0,261 |
0,024 |
0,106 |
0,212 |
|
10 |
1 |
8 |
1 |
0,01 |
0,091 |
0,261 |
0,020 |
0,098 |
0,196 |
|
10 |
7 |
1 |
2 |
0,053 |
0,161 |
0,234 |
0,061 |
0,082 |
0,245 |
|
10 |
6 |
2 |
2 |
0,041 |
0,141 |
0,234 |
0,052 |
0,086 |
0,259 |
|
10 |
5 |
3 |
2 |
0,032 |
0,123 |
0,234 |
0,043 |
0,087 |
0,261 |
|
10 |
4 |
4 |
2 |
0,025 |
0,108 |
0,234 |
0,037 |
0,085 |
0,256 |
|
10 |
3 |
5 |
2 |
0,020 |
0,094 |
0,234 |
0,031 |
0,082 |
0,247 |
|
10 |
2 |
6 |
2 |
0,016 |
0,083 |
0,234 |
0,026 |
0,079 |
0,237 |
|
10 |
1 |
7 |
2 |
0,010 |
0,074 |
0,234 |
0,023 |
0,075 |
0,226 |
|
10 |
6 |
1 |
3 |
0,041 |
0,121 |
0,210 |
0,045 |
0,056 |
0,225 |
|
10 |
5 |
2 |
3 |
0,032 |
0,104 |
0,210 |
0,038 |
0,058 |
0,231 |
|
10 |
4 |
3 |
3 |
0,025 |
0,090 |
0,210 |
0,033 |
0,058 |
0,231 |
|
10 |
3 |
4 |
3 |
0,020 |
0,078 |
0,210 |
0,029 |
0,057 |
0,229 |
|
10 |
2 |
5 |
3 |
0,016 |
0,068 |
0,210 |
0,025 |
0,056 |
0,224 |
|
10 |
1 |
6 |
3 |
0,010 |
0,060 |
0,210 |
0,022 |
0,054 |
0,217 |
|
10 |
5 |
1 |
4 |
0,032 |
0,088 |
0,188 |
0,033 |
0,040 |
0,199 |
|
10 |
4 |
2 |
4 |
0,025 |
0,074 |
0,188 |
0,029 |
0,040 |
0,201 |
|
10 |
3 |
3 |
4 |
0,020 |
0,063 |
0,188 |
0,025 |
0,040 |
0,201 |
|
10 |
2 |
4 |
4 |
0,016 |
0,054 |
0,188 |
0,022 |
0,040 |
0,199 |
|
10 |
1 |
5 |
4 |
0,010 |
0,048 |
0,188 |
0,020 |
0,039 |
0,196 |
Таблица 8 - Универсальные коэффициенты важности критериев в задачах принятия решений с тремя группами важности (окончание)
|
Общее количество критериев |
Распределение критериев по группам важности |
Универсальные коэффициенты важности критериев в свёртке Лапласа F = V ” , a f ^ min Z—/ i = 1 iJ i (по [14]) |
Универсальные коэффициенты важности критериев в свёртке Гермейера F = max a i f i ^ min i = 1,..., ” (по [16]) |
||||||
|
n |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
B1 |
B2 |
B3 |
|
10 |
4 |
1 |
5 |
0,025 |
0,061 |
0,168 |
0,025 |
0,029 |
0,174 |
|
10 |
3 |
2 |
5 |
0,020 |
0,051 |
0,168 |
0,022 |
0,029 |
0,175 |
|
10 |
2 |
3 |
5 |
0,016 |
0,043 |
0,168 |
0,019 |
0,029 |
0,175 |
|
10 |
1 |
4 |
5 |
0,010 |
0,038 |
0,168 |
0,017 |
0,029 |
0,173 |
|
10 |
3 |
1 |
6 |
0,020 |
0,041 |
0,150 |
0,019 |
0,022 |
0,153 |
|
10 |
2 |
2 |
6 |
0,016 |
0,034 |
0,150 |
0,017 |
0,022 |
0,154 |
|
10 |
1 |
3 |
6 |
0,010 |
0,03 |
0,150 |
0,015 |
0,022 |
0,153 |
|
10 |
2 |
1 |
7 |
0,016 |
0,028 |
0,134 |
0,015 |
0,017 |
0,136 |
|
10 |
1 |
2 |
7 |
0,010 |
0,024 |
0,134 |
0,014 |
0,017 |
0,136 |
|
10 |
1 |
1 |
8 |
0,010 |
0,021 |
0,121 |
0,012 |
0,014 |
0,122 |
1,2
Рисунок 2 – К приближённому вычислению универсальных коэффициентов важности критериев при трёх группах важности
-
6 Алгоритм формирования таблиц универсальных коэффициентов важности критериев при любом числе групп важности
На первом шаге алгоритма формулы (7) и (8) позволяют для каждой цепочки формируемой таблицы рассчитать значения коэффициентов, окаймляющих соответствующую ей строку универсальных коэффициентов, а также частично заполнить внутреннюю часть ряда строк.
На втором шаге алгоритма последовательно просматриваются все не полностью заполненные строки универсальных коэффициентов и в тех из них, в которых неустановленным остаётся лишь один коэффициент, он вычисляется исходя из условия равенства единице суммы коэффициентов при всех критериях.
На третьем шаге используется описанный в [14] краевой эффект для того, чтобы распространить уже рассчитанные значения универсальных коэффициентов на новые совпадающие крайние части цепочек.
Затем шаги, начиная со второго, повторяются до полного заполнения всей таблицы.
-
7 Формула вычисления универсальных коэффициентов важности критериев при любой политике выбора
Логика описанного алгоритма позволяет получить общую формулу для расчёта точных значений универсальных коэффициентов важности для n критериев для любой заданной це-
EN j 1ij
= n .
0,8
0 0,1 0,2
y = 1,3188x0,6725
RS = 0,9817
• >- y = 0,6094x1,7893
H--------------------Г RS = 0,9906 • • ...•••• ■
П--Г-^Й^Т—--г
0,3 0,4 0,5 0,6 0,7 0,8
0,9
Обозначим эти коэффициенты a n. , j = 1,..., N , / N = 1 i j = ” . / N i a n.,, = 1.
Для критериев, отвечающих левому элементу цепочки, по определению, универсальный коэффициент важности равен
-
(10) a n, , = a n . .
Для того, чтобы найти коэффициент, отвечающий второму слева элементу цепочки, рассмотрим вспомогательную цепочку i1, i2, (n - i1 - i2). Для отвечающих ей универсальных коэффициентов важности критериев известны левый и правый коэффициенты (по (8) и (7)), а тогда
1 — ia L — ( n — i — i n) a r
~ 2 _ 1 ni 1 V 1 27 ni ( n — i1 — i 2 )
anii ■
2 i 2
Но из цепочки ii, (n - ii) следует, что 1 — i^a t = (n —i2)arni , поэтому (9) переходит в n .1 n,(n—i 2 )
„ 2 _ ( n — i 2 ) a ^ ( n — _2 ) — ( n — h — i 2 ) a r ( n —,_ i 2 )
a* 2
i 2
Аналогично, для третьего слева элемента исходной цепочки, рассматривая вспомогательную цепочку i 1 , i 2 , i 3 , ( n - i 1 - i 2 - i 3 ), получим
1 — ital; — iiat; -( n — i — i n — i n) a r
3 1 ni 1 2 ni 2 v 12 3/ ni ( n — i 1 — i 2 — i 3 )
ani, =------------------------------:------------------------------- ,
3 i 3
и далее, следуя изложенным соображениям,
3 a ni3
( n — i i — i n) a r - ( n — i — i 2 — i n) a r
V 127 ni ( n — Z 1 — i 2 ) v 1 2 3 7 ni ( n — i 1 — i 2 — i з )
i 3
Обобщая (10) - (13), получим общую формулу для универсальных коэффициентов важ-N ности критериев любой цепочки zi, z2,^, in, / ,,_1 i, = n :
a
j nij
aln4 ПРи j = 1,
( n — У j 1 q ) ar j-\ — ( n — У j q ) ar „v
V ^q=14 7 n,(n —/Jj=1 q ) V ^q =1 У 7 n,(n—/=1 q) ij aniN пРи j = N,
при ,j = 2,..., N — 1,
или
a
j nij
aV при j = 1, ( n — ( j 1) j ) a r
2 n ,( n
( j - 1) К
—
( n —
j ( j + 1) 2
) “in — j ))
ij a ri N при j = N .
при j = 2,
N — 1,
Обсуждение
Полученные формулы для расчёта универсальных коэффициентов важности критериев обеспечивают достаточно простое использование методов обоснования многокритериальных решений в самых различных областях. Для этого, в случае распределения критериев между двумя–тремя группами важности не требуется специальных компьютерных программ, достаточно воспользоваться компактными таблицами 7 и 8. Для таблиц от двух до пяти групп важности можно издать компактный справочник для ЛПР. Видно, что размер таблицы универсальных коэффициентов важности критериев до n критериев при N группах важности есть число сочетаний из n по N , т.е. C nN .
Программа, использующая представленные в статье формулы, снимает любые ограничения на размеры решаемых задач и позволяет внести новое качество в процедуру принятия решений, т.к. ЛПР получает возможность, не привлекая посторонних лиц (экспертов), многократно анализировать связь своих предпочтений со следуемыми из них решениями.
Полученные расчётные формулы формализуют подход, связанный с политиками выбора и универсальными коэффициентами важности критериев для средневзвешенной и гарантирующей оценок эффективности решений.
Работа выполнена при поддержке РФФИ, научный проект № 18-08-00858 А, 09.02.2018.
Список литературы Формулы для вычисления универсальных коэффициентов при принятии многокритериальных решений
- Ларичев, О.И. Теория и методы принятия решений / О.И. Ларичев. - М.: Логос, 2002. - 392 с.
- Ларичев, О.И. Вербальный анализ решений / О.И. Ларичев // ИСИ РАН. - М.: Наука, 2006. - 181 с.
- Черноруцкий, И.Г. Методы принятия решений / И.Г. Черноруцкий. - СПб.: БХВ-Петербург, 2005. - 416 с.
- Лебедев, А.А. Курс системного анализа / А.А. Лебедев. - М.: Машиностроение/Машиностроение-Полет, 2010. - 256 с.
- Johannes, J. Vector Optimization: Theory, Applications, and Extensions / J. Johannes. - Berlin, Heidelberg, New York: Springer-Verlag, 2010. - 460 p.


