Формулы физических законов в гиперкомилексной среде: теории относительности

Данная работа продолжает серию статей, посвященных поиску математических соотношений, описывающих физические закономерности, в среде гиперкомплексных чисел. В двух предыдущих работах изложен следующий материал. В работе [1] дано детальное описание ассоциативных по умножению алгебр и структур гиперкомплесных чисел. В работе [2] показано, что фундаментальные условия, обеспечивающие существование и стабильность этих алгебр, имеют свои следствием серию соотношений, которые при формулировке их в стандартных физических единицах представляют собой логически связанную серию уравнений квантовой, классической и релятивистской механики частицы.

В предлагаемой ниже работе речь пойдет лишь о подмножестве указанных гиперкомплексных чисел - кватернионов (и бикватернионов), правило умножения базисных единиц которых² 1qk = qk 1 = qk ， qkqi = — Ski + £ 左叮 qj не ігзменяет своего (формата при преобразованиях векторных едііііііті qk 三 Ok ' nQn 、 Okn G SO(3, C)³. Этот ( } ) акт позволяет выделить в структуре алгебры математические соотношения, являющиеся точными аналогами базовых соотношений теории относительности. В разделе 2 показано, что использование кватернионного репера в качестве базиса системы отсчета наблюдателя позволяет определить векторный базисный объект теории относительности -кватернионный корень квадратный из элемента четырехмерной длины. Показано, что при этом все релятивистские эффекты сохраняются. В разделе 3 демонстрируется, что предложенная векторная версия теории позволяет существенно упростить решение кинематических задач релятивистского движения для наблюдателей, находящихся в неинерциальных системах отсчета. Расчет серии эффектов быстрого движения космических объектов, наблюдаемых с Земли, предложен в разделе 4. В разделе 5 обсуждается особенности топологии модели вселенной, возникающие в векторной версии теории относительности; показано, что эти особенности, однако, не препятствуют развитию в рамках данной теории релятивистской динамики, в том числе, формулировки варианта релятивистской задачи двух тел. В заключительном разделе 6 кратко обсуждаются перспективы дальнейшего исследования.

2.    Кватернионные системы отсчета и релятивистская кинематика

Векторные единицы кватернионной алгебры геометрически представляют собой ортонорми-ровапный базис, или триаду qk, компоценты 2 х 2-матричиого представления которой могут содержать переменные параметры. Поскольку любые триады локально задают область 3D-пространства, ниже будет рассматриваться их зависимость только от точек физического пространства (координат) и времени. Если с началом триады связывать позицию физического наблюдателя, то такая триада может рассматриваться как система отсчета, вообще говоря, движущаяся. Есть физическое различие между триадами, явно зависящими лишь от действительных параметров и триадами, векторы которых суть функции комплексных параметров.

Действительно, триада, векторы которой преобразуются матрицами подгруппы SO(3, R), с точки зрения геометрии, совершает поворот относительно исходного положения на некоторый действительный угол. Каждый пространственный вектор a 三 ak q k при любых таких поворотах остается неизменным a 三 @n Q n = aw q k ， , хотя компоненты его, конечно, изменяются a^ = QnOnk ， . Типичный такой поворот - «простое вращение» - представляет собой поворот всей триады вокруг одного из ее векторов; например, поворот на угол а вок руг q3, такое вращение удобно представить упрощенной понятной формулой q ‘ 三 R$ q・ Параметры подобных простых вращений (здесь а) па^зыватотся углами Крылова [3]. Триада, осуттіествлятошая пространственные повороты. ( ?та.-нет вращающейся (неинерциальной) системой отсчета, если действительные параметры - углы поворота - зависят от времени наблюдателя (то есть триаду нужно дополнить часами).

Ситуация меняется, когда векторы триады преобразуются матрицами группы SO(3, C), компоненты которых содержат комплексные параметры. Правило умножения единиц алгебры при этом не нарушается, но каждое такое преобразование превращает вектор кватернион в бикватернион. Физически значимым оказывается выделение подмножества векторных бикватернионов вида s 三(an + ibn)qn (!) с «определяемой нормой»

s² = b² - a², (2)

что возможно при условии ортогональности действительной и мнимой составляющих an bn = 0. Это условие, всегда выполняется, когда вещественный и мнимый векторы направлены вдоль разных составляющих триады, например s 三 ibiqi +a2q2 (3)

Иными словами, вектор (1, 3) есть (шестимерный) бикватернионный «корень квадратный» из скаляра (2). Несложно доказать теорему [3, 4], которая гласит, что вектор (3) сохраняет свою форму s 三 ibiqi +。2《2 = ibi,qi, +。2,q2,, (4)

если векторы триады преобразуются SO(3, С)-матрицами, представляющими собой сумму простых вращений, выполняемых в произвольном порядке, но с действительным параметром (углом поворота) относительно «мнимой оси» и мнимым параметром - относительно «вещественной оси». В целом такое преобразование реализуется произведением соответствующих матриц, образующих подгруппу SO(1,2) С SO(3, C). Понятно, что простое врашешк? с мнимым параметром является гиперболическим.

Соотношение форм-инвариантности (4) можно рассматривать как математический аналог следующего «физического» равенства ds 三 idtqi + drq2 = idt'qi, + dr'q2,, (5)

rje dr. dt — изменения координаты частптіы ii интервал времени ііаблтодеішя < ) того изменения в триаде Е 三 q k ， dr', dt'. — соответствутошпе параметры движения в другой триаде Е' 三 q k ， . некоторым образом, движущейся относительно Е; фундаментальная скорость принята за единицу. Здесь нужно сделать два следующих существенных замечания. Во-первых, поскольку в данном случае (мнимое) время измеряется вдоль одного из векторов триады, дополнительный хронометр не нужен, так что каждая триада с наблюдателем представляет собой полноценную систему отсчета

(репер). И, во-вторых, равенство (5) будет выполняться, если системы отсчета связаны преобразованием, удовлетворяющим требованиям вышеизложенной теоремы:

W = OE, O е SO(1,2).

⑹

Преобразования (6) оставляют инвариантным также, конечно, и квадрат вектора (5) - квадрат простраііствеііііо-времеішого интервала ds² = dt² — dr², следовательно, кватернионная теория, своего рода «корень квадратный» из стандартной теории относительности, должна содержать все эффекты последней. И это действительно так, поскольку шестипараметрическая группа SO(3, C) изоморфна специальной группе Лоренца SO(1, 3), и легко показать, что матричные элементы этих групп однозначно выражаются друг через [3]. Релятивистские эффекты «содержатся» в уравнениях (5, 6) при задании соответствующих матриц поворота; полезно рассмотреть ряд примеров.

Простой бу ст. Пусть E' есть результат поворота E на гиперболи 工 іеский «угол» i^

cosh η isinh η 0

⑺

—i sinh n cosh n 0   ； тогда из уравнения (5) сразу следует известное преобразование координат и времени dr = dt sinh n + dr cosh n, dt' = dt cosh n + dr sinh n

Если при этом E' — наблтодаемып репер, то dr' = 0. ii величина скорости ее движения относите л ыю репера E определяется (формулой u = dr/dt = tanh 〃.

Сложение скоростей. Пусть реперы E' и E'' движутся отиосителыю E так, что их скорости ui = tanhni- U2 = tanhn2- направлены под углом в ПРУ 「 к другу в пространственной плоскости {q2,4з} реп epa ， E. ii пусть при этом u i 廿 q2- Тогда, штрихованные системы удовлетворятот уравнениям поворота типа (6) E' = 03ⁿ¹E, E'' = 03ⁿ²O ； E, откуда сразу определяются выражения для базисных векторов системы E'' как функций векторов системы E': E'' = 03ⁿ²O ； O—iⁿ1 Е' , или в явной матричной форме

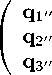
cosh η2

=   —i sinh n2

i sinh η2 cosh η2 0

0)(0

0      0        cosh η1

cosβ sin β i sinh η1

— sin в cos в         0

—i sinh ni  0      qr cosh ni    0       q2f

0      1      qg

Первая строка этого матричного уравнения представляет собой зависимость первого вектора E'' от век торов E''

iqi 〃 = (cosh ni cosh n2 — cos в sinh ni sinh П2 )， 9г +                      (8a)

+ (sinh ni cosh n2 — cos в cosh ni sinh n2 ) q2, — sin в sinh n2Q3 ，

Поскольку в данном случае E'' наблюдается из E', соотношение (5) для этих систем отсчета записывается в виде dt''iqi〃 = dt'(iqr + Uyq?，+ Uzq3，), или полагая dt'/dt'' = cosh n, в виде iqi〃 = cosh n(iqi, + Uy q2, + Uz q3,).

Из соотношений (8) сразу определяется неизвестный гиперболический косинус cosh n = cosh ni cosh 小(1 — Ui • U2)

и следуют формулы для компонент и (квадрата) модуля скорости E'' относителыю E'

Ui — U2 cos в           U2 sin в ， 1 — U2     2   (ui — U2 ) 2 — (Ui X U?)²

uy = ~.            , uz =     ^             , u =      ~          ~2

1 — Ui • U2                 1 — Ui • U2                   (1 — Ui • U2 ) 2

Если реперы E'' ii E' движутся в против ono ложных направлениях в = п. то уравнения (9) сводятся к случаю параллельного движения: u = (ui + U2 ) /(1 + U]U2 ) . Стоит отметить, что рассмотренная здесь задача о сложении скоростей при непараллельном движении релятивистских систем отсчета в специальной теории относительности оказывается более трудоемкой.

3.    Кинематика неинерциальных систем отсчета в кватернионной версии

Параметры преобразований кватернионных триад могут быть функциями координат и времени физического пространства, тогда соответствующие системы отсчета являются неинерциальными. Описание такого движения в векторном формате оказывается весьма удобным, если использовать стандартные для подвижного репера дифференциальные соотношения dqk($) = ®gknqnd@£, дф-qk(Ф) 三 dgqk (Ф) = sgknqn где¹Ф ^ — парам ( ?тры. от которых как (функция ^зависит кватершюп-ная триада. ®gkn — кват ( ?рішоііая свя ： зпость. в ( ?лпчіша. аптіісішм ( ?трпчііая по в ( ? к торным ішд ( ?ксам. Ниже - ряд известных примеров, демонстрирующих удобство метода, и расчет новых эффектов релятивистского неинерциального движения.

Гиперболическое движение. Прямолинейное (вдоль вектора q?) движеиие репера Е' относительно репера Е с постоянным ускорением a ' = const описывается уравнетшем поворота Е ' = 03^n(t )Е. где¹ матрш 【 а 03^n(t) іід ( ?птпчпа (7). но іпк? ( ?т п ( ?р ( ?м ( ?ішы ( ? компоненты, а параметр n(t ' ) нужно определить.

Пусть вначале Е' наблтод ； ается из Е. Тогда, ба'зиснып век тор-иитервал имеет вид (c = 1)

ds = idt ' qr = idtqi + drq?, (10) а вектор ускорения, вычисляемый как вторая производная (10)

a' = d²s/dt'² = idqv/dt' = i^ t i? q 2 = П q2 = a'q2, (11) дает решение для параметра n(t') = a't', постоянная интегрирования (начальная скорость) выбрана равной нулю. Теперь, используя следующее из равенства (10) соотношение dt/dt' = coshn легко найти зависимость времени наблюдателя Е от времени Е'

t(t ' ) — to = / dt ' cosh(a ' t ' )= 二 sinh(a ' t ' ); t ' (t)= 二 In 卜 t + д/1 + (a ' t)²] , to = 0, и все «наблюдаемые» кинематические характеристики: относительную скорость

u(t) = tanh(a't') = tanh[sinh(a't)] = — a =,(12a)

V 1 + (a't)2'

ускорение и координату как функции времени наблюдателя

• a⑴=^ut) =      a '213/2, r(t) = /u(t)dt =!，】+ (a't)2 - !.(126)

dt [1 + (a't)2]3/2                              a'

Но если формулы (12) можно получить в рамках специальной теории относительности [5], то обратная задача о движении инерциального репера, наблюдаемого из равноускоренной системы отсчета, в скалярном (стандартном) формате теории обычно не рассматривается. Но она легко решается в рассматриваемом векторном формате.

Пусть теперь Е наблтодается из Е'. Этой кішематіг-юскоп ситуатцш соответствует обраш.ешюе уравнение поворота Е = O—2n(t )Е' с прежней фуикцией параметра n(t') = a't'； вектор-интервал имеет вид ds = idt'qy — dr'q2，= idtqi, откуда определяется (ожидаемо исчезающий) вектор ускорения инерциального репера a = d2s/dt2 = idqi/dt = 0

и соотношение интервалов времени dt'/dt = cosh 〃♦ Далее по изложенному выше алгоритму вычисляются все кинематические характеристики движения Е, «наблюдаемого» из Е'

t(t') = / dt'/ cosh(a't') =— arcsin[tanh(a't')], to = 0;                     (13a)

a'

• u(t') = tanh(a't'); r' (t') = 31n[cosh(a't')], r° = 0; a(t') =-----a------.          (136)

a'                                            cosh2 (a't')

Как и в предыдущем случае, при малых значениях времени формулы (13) сводятся к формулам иерелятивистского ускоренного движения, но для больших значений времени Е' часы в репере Е замедляются и останавливаются в пределе t^—g т nc/(2a ， ).

Прецессия Томаса. Пусть репер Е постоянно ориентирован относительно «неподвижных звезд» и находится в центре круговой орбиты радиуса R, по которой равиомерио движется репер Е\ ориентированный так же. Требуется найти проекцию q?，на векторы qk притом, что в начальный момент времени q?，ff q?. В иерелятивистском случае всегда q?，= q?, но при больших относительных скоростях должен возникать эффект, называемый прецессией Томаса [6]. В рамках специальной теории относительности расчет этого эффекта достаточно сложен (см., например, [7, 8]), в векторной версии задача решается просто. Репер Е переводит в Е' следующее тройное преобразование: (i) вращение вокруг вектора No 1 на угол ү = ®t; (ii) гиперболический поворот вокруг вектора No 2 на «угол» in, tanhn = ®R = const; (iii) обратное вращение вокруг нового вектора No 1 на угол — ү(t‘) = —®'t‘，что задает прежнюю ориентацию репера Е' относительно «неподвижных звезд». Уравнение такого поворота Е' = O-Y(t )O2nO；Е имеет явный вид qi，           1       0

q? ，   = 0 cos(J ， )

q3 ，           0 sin(® ' t ‘ )

0         cosh n 0 — i sinh n 1

0 0 qi cos(^t) sin(^t) q? — sin(^t) cos(^t) 丿 \q3

— sin(® ' t ‘ )         0      1       0         0

cos(^ ^f t ^f ) 丿 \i sinh n 0 cosh n 丿 \0

откуда с учетом

соотношения t‘ = t/cosh^ определяется, на пример, проекция q? ， ii a q3

〈 q? ， 〉 3 = sin[(^ — J)t] — 2sinh?(n/2) cos(^t) sin(s ' t) = sin(^Tt).

Значит, с точки зрения Е-иаблюдателя, вектор q? ， прецессирует (ретроградно) с постоянной частотой, наибольшая часть которой (по порядку величины) соответствует прецессии Томаса

-2 di

®т 三 ® — J = ^(1 — coshn)

Полезно заметить, что в векторном формате теории относительности несложно рассчитываются эффекты типа прецессии Томаса для орбит произвольной формы, а также аналогичные эффекты, наблюдаемые из неинерциальных систем отсчета (детали см. в книге [4]).

Релятивистский гармонический осциллятор. Пусть репер Е' движется под действием гармонической силы, направленной вдоль q?，, и наблюдается из инерциального репера Е. Эта кинематическая ситуация аналогична рассмотренной выше задаче гиперболического движения, описывается сходным уравнением поворота и базовым интервалом. Но величина собственного ускорения репера Е' (то есть, силы на едпшшу массы) в данном случае должна быть гармонической (функций a' = d?s/d，？ = % q?，= 0，в cosQ^q?，;

злесъ Q' — собственная частота осциллятора, в < 1 一 некоторая постоянная, c = 1. Последнее равенство определяет функцию гиперболического параметра n(t') = в sinQ't', а с ним — соотношение времен

t

/^cosh 小画

/ cosh(e sin Q ' t ' )dt ' .

При условии в < 1 этот интеграл вычисляется точно в вид ( ? ряда (см.. папрпм ( ?р. [9])

， 3 в?^п t=t⁺ns 而

丄 ( 2n 、 t ， . ( — 1)ⁿ ^ _(—]№ ( 2n 、 sin(2n - 2k)Q ' t ' 22ⁿl nJ      2?n-1 £ (   ^! \ kJ (2n — 2k)Q ，

,

(14а)

откуда, при Q ， T ‘ = 2п определятотся сооттюшетшя п ( ?риодов ii частот в Е іі Е '

T

T'

( ОО

】+ Е n=1

в?п 1 (2n)!2?n

2n

n

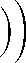
ⁿ=^n, (¹⁺1=5 詫去 (²n ))1. 网>

Из соотношений (146) следует, что в репере Е колебательный процесс представляется более медленным, чем в реальности. Расчет кинематических характеристик осциллятора, наблюдаемого i із E. требует обраш.еш ія (формулы (14а)：，=，(t) что может быть сделано в приближении в v/c《1： V = const:

t' = t -号 (t - ] sin 2Qt).

Относительная скорость реперов определяется стандартной формулой

u(t)

c tanh (в sin Q't')

=v sin Qt

( 1 - 3^в2 +12^в2 cos^{2 Q}t ) ,

согласно которой в начале и в конце периода реперы друг относительно друга неподвижны u(0,T) = 0. а максимальная паблтодаемая скорость есть umax 三 V (T/4) = v ( 1 - в²/3 ) . Таким образом, движение осциллятора E', с точки зрения E, оказывается негармоническим. Наблюдаемые величины ускорения и координаты соответственно получаются дифференцированием и интегрированием функции (15) по времени наблюдателя.

Обратная задача наблюдения инерциального репера E из системы отсчета E', связанной с осциллятором, решается по тому же алгоритму. В этом случае нет необходимости обращать функцию времени, поэтому все кинематические характеристики определяются в виде сходящихся рядов точно, что выделяет эту задачу из многих других релятивистских задач допускающих лишь приближенные решения.

Не лишне также отметить, что данная задача о релятивистском осцилляторе позволяет проанализировать известный «парадокс близнецов» с весьма «физических» позиций. Действительно, если космическое путешествие рассматривать как одно колебание осциллятора E', то «близнецы» покоятся друг относительно друга в начале и в конце движения, где положения их строго совпадают, а также в точке поворота, тогда как околосветовая скорость ракеты на всех частях траектории достигается постепенно (детали см. в книге [4]). Ни одно из вышеперечисленных условий не выполняется при анализе этого парадокса в рамках специальной теории относительности.

4.    Наблюдаемые с Земли релятивистские эффекты в ближнем космосе

Векторный формат теории относительности весьма удобен для моделирования широкого спектра кинематических ситуаций в неинерциальных реперах, в том числе и таких, где телом отсчета является Земля. Это позволяет рассмотреть ряд релятивистских эффектов в масштабах Солнечной системы, где скорости тел уже значительны, а скорость света не представляется слишком большой величиной, так что такие эффекты становятся заметными.

Релятивистский сдвиг спутников планет. Пусть Земля (репер E) и планета (репер E') движутся вокруг Солнца по круговым орбитам с постоянными линейными скоростями VE, VP, и пусть при этом разность их угловых орбитальных скоростей есть Q 三 QE — Qp = const; все величины измерены земным E-ііаблюдателем. Тогда гиперболический параметр n(t) 《 1, определяющий стандартное соотношение времен t = t'coshn, с достаточной точностью определяется из геометрии треугольника скоростей

V2 = VE + VP — 2VE V p cos Qt = c² tanh² n.

Пусть наблюдаемая планета имеет спутник, ^' = const — его собственная угловая частота обращения по орбите радиуса r = const. В силу соотношения времен частота, наблюдаемая с Земли, оказывается меньше ® = ^'/coshn, то есть часы «релятивистски отстают». Несложно найти наблюдаемый угол положения спутника относительно его позиции в некоторый начальный момент времени

90bs (t) = / 3dt = J / dt/ cosh n(t) = ^'t {卜 — 白 (VE + Vp) ] + VcVP sinQ," } , а затем - выражение для наблюдаемого с Земли (кажущегося) орбитального сдвига спутника

△ 1 三 r(9obs — 9real) = - VE^^ 『口^ + ^^ sin^" Гз' .               (16 )

2c2            c2     Ω

Видно, что этот эффект накапливается со временем и, кроме того, движение спутника наблюдается как неравномерное с переменным ускорением

VE VP aobs =--5—r®'Qsin(Qt);                                  ( L )

c2

эти факторы могут оказаться физически значимыми. В частности, расчет показывает, что самые быстрые спутники Юпитера - Метида и Адрастея - за 10 лет наблюдений «релятивистски отстают» от своего реального положения на расстояния, существенно превышающие их размеры И-

Однако, как показали астрономические наблюдения и теоретические исследования конца XX века, эффект орбитального сдвига может иметь серьезное практическое значение. Действительно, в многолетних наблюдениях Фобоса, быстрого спутника планеты Марс, замечена существенная неравномерность его движения по орбите притом, что построить удовлетворительную теоретическую модель этого движения на базе классической механики сложно (см., например, [10-13]). Кроме того, известно, что космические аппараты, направляемые к Марсу и тем более к Фобосу, либо оказываются неуспешными (в связи с необъяснимой потерей аппарата), либо обнаруживают Фобос на траектории с существенным опережением его ожидаемой (расчетной) позиции. Ссылки на соответствующие источники приведены в работе [14], где также показано, что расчет положения и ускорения Фобоса с помощью формул (16, 17) дает значения величин в пределах астрономических измерений и установленных экспериментально в ходе космических миссий. Так, цитируемые в литературе экспериментально измеренные значения ускорения Фобоса a _exp = +1.88 х 10^-3град/год² (см. [10]). aexp = -0.83 х 10^-3град/гс ) д² (см. [11]) не превышатот предельных зиачеипп ускорения aiimit = ±4.84х 10^-3град/гс ) д². рассчитанных по (формуле (17). А отмеченное станциями «Маршюр-9» (1971 г.) и «Марс Экспресс» (2004 г.) «опережение» спутником на несколько километров его ожидаемого положения соответствует значению △ / = 5.18 км, рассчитанному по формуле (16) при условии, что в бортовой компьютер космических аппаратов закладывались данные орбитальных параметров Фобоса, полученные в период противостояния планет 8-летней давности. Таким образом, наблюдаемые неравномерности движения и запаздывание Фобоса вполне могут рассматриваться как следствия обсуждаемого релятивистского эффекта.

Данная теория был также применена для оценки успешности российского проекта «Фобос Грунт», реализация которого планировалась в 2011 году. В результате было сформулировано «релятивистское предупреждение» [14], предсказывающее возможный «пролет» космического аппарата мимо Фобоса в случае пренебрежения эффектом релятивистского сдвига. Проверить справедливость этого предсказания, к сожалению, не удалось, так как аппарат потерпел крушение на начальном участке своей траектории.

Релятивистское объяснение «аномалии Пионера». Космический зонд Пионер 10 (США) был направлен к границам Солнечной системы в 1972 году и более 20 лет передавал сигналы на Землю. Анализируя эти данные на базе эффекта Доплера, специалисты НАСА обнаружили аномальное замедление зонда [15] с почти постоянным (отрицательным) ускорением ар = — (8 ± 3) ・ 10^-8см/год2. Аналогичный эффект был отмечен для зонда Пионер 11. Это сообщение вызвало серию попыток объяснить «аномалию Пионера», в основном, влиянием новых физических факторов (см. статью [16] и ссылки в ней). Однако построение простейшей кинематической схемы «наблюдатель-зонд» в рамках векторного формата теории относительности показало, что эта «аномалия» может быть релятивистским эффектом, ранее не учитывающимся в силу его предполагаемой малости.

Пусть «неподвижный» репер Е связан с Солнцем (массой М), а репер Е' — с зондом (массой m). двпжушпмся прямолпиепио вдоль направления q2 с переменно и скоростью u(t). Урашіешіе поворота Е' = O—2ⁿЕ в «плоском мире» имеет следствием стандартное соотііошеіше времен dt = dt'coshn и выражение наблтодаемоп в Е частоты сигнала f (t) как (функции геиерпруемоп зондом частоты f' = const

f(t) = f7 cosh n = f ' ， 1 - (u/c)² = f' (1 — 2c2).

Отсюда вычисляется относительная разность истинной и наблюдаемой частот, возникающая как следствие эффекта «замедления времени»

' и ²

△ f/f' = 一 =   = Е%                     ( 18 )

f'       2c2

rje е — кинетическая внертя зонда на едпшш.у его массы. Если величина (18) определяется в результате эксперимента, то наблюдатель может придти к ложному выводу о том, что изменение частоты есть результат движения зонда относительно наблюдателя с некоторой дополнительной (кажущейся) скоростью ик, в результате чего возникает эффект Доплера

f

f'

,1 - (uK/с)2

1 -

uK c cos γ ,

где1 ү — угол мс'жду вектором скорости ик ii волновым вектором сигнала. В случае ：зоида Пионер 10 этот угол мал ү — 0； из формулы (19) тогда следует ик = cAf/f и, с учетом соотношения (18), определяется величина кажущейся скорости uK ∼= ε/c.

В рамках классической механики и гравитации Ньютона полная энергия зонда постоянна Ео 三 mf - GMm/r = const rje G — гра.вігтатіііоішая постоянная, r — расстояние Е-Е\ то есть £ = Ео/m + GM/r. По,установка，второ выражения в уравнение (20) п діі(})(})ереішііроваіше последнего по времени дает формулу расчета кажущегося ускорения (замедления) зонда aK ≡ u˙ K = -uGM/(cr2).

Если же рассматривать этот эффект не в «плоском мире», а в рамках общей теории относительности, где поле тяготения Солнца описывается решением Шварцшильда, то в соотношение времен появляется дополнительное «гравитационное» слагаемое [16]

dt = dt‘

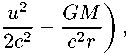
так что величина кажущегося замедления по сравнению с формулой (21) удваивается aK = -2uGM/(r2).

Подстановка в (22) констант c = 2, 99 • 1010 см • с-1, G = 6, 67 • 10-8 см3 • г • с2, M = 1, 99 • 1033 г и параметров зонда Пионер 10 на среднем этапе его наблюдений (1983-1990 годы) u = (1,52 — 1,41) • 106 см/с_ r = (4, 3 — 7, 2) • 1014 см (из данных НАСА [17]) ,і,ает диапазон значений кажушегося ускорения ак = —(7, 27 — 2, 61) • 10-8cz • с-2, что сравнимо с приведенными выше экспериментальными данными. Здесь стоит сделать ряд замечаний. Из формул (21, 22) следует, что если «аномалия Пионера» является релятивистским кинематическим эффектом, то, будучи обратной функцией квадрата расстояния, наблюдаемое ускорение не может быть постоянным (как вначале полагали авторы наблюдения), но должно уменьшаться со временем. Последующий анализ экспериментальных данных показал [18], что абсолютная величина ускорения действительно уменьшается, для Пионера 10 это уменьшение составляет Аар 仁 2 • 10-9 см • с-2 • г( эд-1. С помошьто (формулы (22) не сложно р ас ст-п гтатъ среднегодовое изменение модуля кажущегося ускорения зонда в конце среднего этапа наблюдений (1991 год), приняв, согласно [17], г+го几=7, 2 • 1014 см, r = 7, 58 • 1014 см,

Аак = 2uGM (-1---1) = 2, 51 • 10-9 cn • с-2 • roL, c   \r+s   r2 丿 что соответствует экспериментальным данным.

На основании изложенной здесь теории и приведенных расчетов приходится сделать вывод о том, что релятивистский (и гравитационный) эффект изменения частоты сигнала, принятый за часть эффекта Доплера должен являться заметной составляющей «аномалии Пионера» и учитываться при объяснении этого феномена.

5.    Динамика тел в кватернионной версии теории относительности

Таким образом, векторный формат теории относительности оказывается весьма удобным для вычисления реальных физических эффектов на уровне кинематических соотношений. Не менее удобен он и для описания динамики релятивистских механических систем. Однако, прежде чем перейти к динамическим уравнениям, стоит отметить, что эта теория предполагает топологически своеобразную модель вселенной, насчитывающую не четыре измерения, как в стандартной теории относительности, а шесть измерений. Локально такую вселенную можно представить как две трехмерные области, в одной из которых сосредоточен действительный SD-мир наблюдателя, а вторая представляет собой «мнимый» SD-мир, где наблюдатель мысленно выделяет направление изменения времени [4]. При этом расстояния мнимого мира, как и действительного, измеряются в единицах длины, а интервал времени определяется наблюдателем как отношение мнимого расстояния к величине фундаментальной скорости. Такая вселенная «симметрична по сопряжению», то есть в каждом из SD-миров, взаимно мнимых по отношению друг к другу, может находиться наблюдатель, считающий свой мир действительным. Но при этом следует полагать возможным и наличие наблюдателя в «параллельном мире». На сегодняшнем уровне понимания строения физического мира такая модель является абстракцией, поскольку пока она отражает лишь суть математических структур, «правильно» описывающих известные явления. Не исключен, впрочем, и иной взгляд на реальность данной модели. Приведенные здесь пояснения нужны для введения понятий о мнимых компонентах векторных (тензорных) величин, возникающих в 6-мерной модели.

Базовой величиной динамики в кватернионной теории относительности является вектор импульса. Пусть две взаимодействующие частицы с массами покоя Mo и m° являются соответственно телами отсчета реперов Е и Е\ вообще говоря, не инерциалыіых. Если тело отсчета Е' наблюдается из репера Е. то вьшо/няе 工 ся равенство типа (5)

ds = icdt'qv = icdtqi + drq2,

вектор q2 всегда параллелен вектору отиосптелыюп скорости. Эта ситуация описывается уже известным уравнением поворота Е' = ОПЕ. Несложно показать, что, помимо базисного вектора-интервала (23), замечательным свойством форм-инвариантности обладает также и вектор импульса. Действительно, из определения импульса наблюдаемого тела в его собственной системе отсчета Е' с учетом соотношения времен dt = dt'coshn следует

P'

ds dt m0

dt dt'

ds     ds mo coshndt = mdt = P,

где, как в специальной теории относительности, пульса по компонентам реперов определяется из

принято m = mocoshn Разложетше вектора іш-соотношений (23, 24)

P' = imocqr,

(25а)

P = mo cosh n (icqi + uq2 ) .                                (256)

Уравнение динамики как закон изменения импульса под действием силы можно записать в формате уравнений Ньютона с позиций разных системы отсчета.

В репере Е' от времени t' зависит направлятошпп вектор времени qv (t'). Проігзводная по t' собственного импульса (25а，) выражается qepe：3 компоненты связности, вводимые по правилу dyqw = Qk，" q〃,- или в развернутом виде d#P' = m°ic (Qi,2，q2, + ОгзУз,), где компоненты связности описывают соответственно собственное касательное и нормальное ускорение репера Е'

Qi,2 ， = —i 。 ？ ,/с, Оуз ， = —іаз,/c.

Если определить силу как произведение массы покоя Е'-иаблюдателя и ускорения, которое он ощущает (измеряет), F' = moak，q^, то динамка в репере Е' описывается соотношением, имеющим формат уравнений Ньютона dt，P' = F'.

Соотношение (26) удобно использовать при решении обратной задачи механики для наблюдаемого тела ： Е^z-11 аб лтодатель. ішстру ментально измерив собственное ускорение п зная собственник) массу покоя, может вычислить компоненты действующей на него силы.

Для Е-иаблтодателя также можно ：записать уравнетше тіша，(26) dy P' = F'： после nii(J)(j)epeii-цирования импульса (256) по времени t оно принимает вид dtP = mo [nsinhn(icqi + uq2) + coshn (icQi2Q2 + ісОіз9з + Uq2 + u^2iqi + u^23q3)] = FkQk, (27)

где по правилу dtqk = OknQn введены компоненты связности, отождествляемые с нормальной и касательной компонентами Q12 = -ha?/с, Q13 = -іаз/с собственного ускорения репера Е и с угловой скоростью Q23 三 Q его поворота в плоскости векторов q? и q3. При этом векторное уравнение (27) записывается в компонентах следующим образом im^ (сП + a?) = iFi, c

(28а)

т(сП + a?) = F2,

m(uQ + аз) = F3. (28в)

Уравнения (28) описывают динамику релятивистского тела (репера Е‘), движущегося под действием некоторой силы и наблюдаемого из, вообще говоря, ііеинерциалыіого репера Е, вектор q? которого постоянно пар а 〕「 е, 「 е н вектор у отиосптелыюп скорости реперов. '9 та спет ем а ， ур ав -нений имеет две существенные отличительные черты. Во-первых, здесь присутствует временная (мнимая) компонента силы Fi, наличие которой связано с 3—3-симметрией вселенной в данной модели: подобно тому, как сила F? изменяет величину относительной скорости, следовательно, масштаба пространства, так сила Fi симметрично изменяет масштаб времени. Впрочем, компонента (28а), пропорциональная компоненте (286), не влияет на математическое содержание уравнений. Во-вторых, релятивистский характер динамики очевидно подтверждается тем, что в полученной системе уравнений вместо производных скорости по времени фигурируют производные гиперболического параметра. В целом эта система позволяет решать прямые и обратные задачи динамики и при малых значениях u/c сводится к классической системе уравнений Ньютона.

Взаимосвязь ускорений. Взаимозависимость между собственным ускорением репера Е' и компонентами его ускорения, наблюдаемого из системы отсчета Е, устанавливается с помощью уравнения поворота Е' = ОПЕ, из которого следуют соотношения qv = cosh nqi — i sinh nq?, q?，= i sinh nqi + cosh nq?, q3，= q3, dt，= cosh 〃dt.

После подстановки этих соотношений с учетом свойства инвариантности (24) уравнение (26) приводится к виду dtP = m

(Va? ， iqi + a? ， q? + -^93);

\ c                 cosh n 丿

сравнение коэффициентов при векторах qk в уравнениях (27) и (29) дает формулы искомой взаимосвязи касательного и нормального ускорений a?，= c力 + a?,  ——--=V Q +a3.

(30а)

cosh n

Эти соотношения полезно переписать в виде сП = a?，— a?,

V О = -03---a-, cosh n

явно демонстрирующем особенности релятивистской динамики. Действительно, разность касательных ускорений реперов определяет наблюдаемое касательное ускорение, которое здесь выражается как производная по времени от гиперболического параметра (а не от относительной скорости). Наблюдаемое же нормальное ускорение (заданное здесь модулем векторного произведения относительной скорости реперов и угловой скорости вращения репера Е) есть релятивистски скорректированная разность собственных нормальных ускорений вовлеченных систем отсчета.

Несложно проверить, что при условии V/c 《 1 соотношения (306) сводятся к классическому случаю.

Стоит добавить, что последние соотношения имеют простой геометрический смысл, по сути, являются следствием того факта, что кватернионная связность не является тензором относительно преобразований репера. Для частного случая связности Qkn эта формула имеет вид

Qk，n，= OkjOn，mQjm + dtOkjOnj, тензорные свойства «портит» последнее слагаемое. В случае используемого здесь простого преобразования Е' = ОП Е только две компоненты отличны от нуля

01,2，=012 -i3,   01,3‘ = cosh ^Qi3 - i sinh 3。23； подстановка сюда принятых выше обозначений компонент связности через собственные ускорения реперов приводит в точности к уравнениям (30а). Таким образом, уравнения релятивистской динамики представляют собой отражение геометрических свойств рассматриваемого кватернионного пространства.

Формулировка релятивистской задачи двух тел. Пусть Mo и m° — соответственно массы покоя тел отсчета реперов Е и Е\ взаимодействующих между собой. Тогда, с позиций базового репера Е. компоненты ускорений с л еду тонн im образом выражатотся qepe ： 3 компоненты силы

@2, = F2 ， /mo, 。 2 = F2/Mo, 。 3, = F3/mo, 。 3 = F3/Mo.                 ( 3D

Здс'сь Fk，. Fk — компоненты свя^зутошей силы, депствутошеп соответственно на Е' іі Е. при этом касательное ускорение определяется через релятивистскую массу m = mo cosh п наблюдаемого репера Е'. так как в внеш направлении есть относителыюе движение： нормальное ускорение определяется через массу покоя. Подстановка определений (31) в уравнения (306) приводит к следующей простой системе динамических уравнений сП = F2/m - F2/M0, VQ = F3/m - F3/Mo.                   (32а)

В силу симметричности механической ситуации, аналогичная система должна быть записана для базы Е'. из которой наблтодается репер Е

- сП = F2 ， /M - F 》/ mo, - VQ = F3 ， /M - Fg/mo,                 (326)

но с учетом противоположного знака относительной скорости и необходимости проводить все вычисления во времени t'.

Уравнения (32) представляют собой систему уравнений релятивистской динамики двух взаимодействующих тел. Существенно заметить, что все компоненты сил оцениваются конкретным наблюдателем в определенный момент времени (t или t'). Эти уравнения весьма удобно использовать для приближенного решения широкого круга задач с учетом эффектов запаздывания взаимодействий и сигналов. Несложно показать, что эти эффекты, как минимум, пропорциональны V/c при условии, что скорость передачи взаимодействия (как и электромагнитного сигнала) конечна. Например, если на тело Е со стороны тела Е' действует перемеииая сила F[r(t)], то с точки зрения Е-иаблтодателя. на тело Е'. находяшееся на расстоянии г. такая же по модул то сила со стороны Е будет действовать с запозданием F '[r(t)] = - F [r(t + At)], At = r/c. Ес ли At/t 《 1, to

F'[r(t)] = F[r(t)] + dF dr At = F[r(t)] + rdF V, dr dt                 dr c rje V — радиальная компонента относителыюй скорости. Подстановка данного разложетшя в систему (32а), очевидно, требует поиска решения до первого порядка по V/c, что достигается представлением радиальной скорости в виде классической и релятивистской составляющих Г = VC + VR, Vr《VC-

Впрочем, даже в тех случаях, когда параметры запаздывания пренебрежимо малы (статическое поле сил, малы расстояния между телами, малы градиенты силы), в решения могут проявляться эффекты, отражающие релятивистскую специфику динамических уравнений.

Показательный пример - задача движения частицы в поле большой массы. Пусть тело с мас-со 甘 Mo является т ( ?лом системы отсчета наблтодателя Е. неподвпжиоп (。左= 0). но допускатошеп повороты, и пусть это тело есть источник поля центральной силы, в котором движется частица

Е' с масс 。 ii покоя m°* Mq 》 m° ： пож? силы статическое. ' ；)( 1 )( 1 ) ект ： запа'здываішя не учптыва ( ?тся (задача будет решаться в приближении малых относительных скоростей).

Поскольку вектор импульса частицы форм-инвариантен по отношению к преобразованиям поворота, уравнение динамики можно записать (и решать) в любом допустимом репере. В данном случае удобно использовать следящий репер, вектор q2 которого задает направление радиуса-вектора частицы r = rq2 ； тогда о невидно F = Fq?. Вектор импульса частицы (256) в следящем репере записывается так

P = mo coshn(iV1qi + V2q2 + V3q3)三 m(icqi + rq2 + гв9з), злесъ в — угол поворота репера Е. m = mocosh п- Динамические уравнения dtP = F пр(?дста.влеиы системой

ітП V = iF1,

(33а)

m

(Vn r + r - ^c

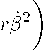
F,

m

V

I —Пгв + 2гв +

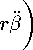
0,

(ЗЗв)

С V = (Г² + r²в²)^1/2 — модуль скорости частицы. При условии F1 = (Г/с)Ғ уравнение (33а) является следствием уравнений (326, 32в), так что достаточно решить два последних уравнения системы. Стандартная подстановка а 三 г²в в уравнение (32в) дает первый интеграл системы а = г² в = oq/ cosh n(t )-。 0 = const- то есть секторная скорость а в ре пере Е переменна, но модуль

момента импульса — величина постоянная L 三 ma = т 。 。 。 . При этом из уравнения (326) после

умножения его на

rcosh п следует шгтстрал 'Әпергіш

m2⁰ (r² cosh² n + ,) + U = E = const, no

в предположении, что dUr) = dUr) (1 + PVY где

натуральное число. Выражая из интеграла энергии

решение последнего дифференциального уравнения

U — какой-то классический потеішііал. Р —

V²/(2c²) = (E - U)/m 。 << 1. легко найти

U = U

+ Uo,

Uq = const.

Теперь можно найти вторые интегралы движения. В частности, равенство дифференциалов времени, вычисленных из интегралов секторной скорости и энергии, имеет своим следствием уравнение траектории

^в(г) — ^в 。 = / °₂   ---^(E0 — U)--⁰    , ^в 。 = Const,

/   r2   mo            r2

формально классическое, но с потенциалом (34).

Формула (35), примененная для расчета релятивистских поправок к задаче Кеплера с потенциалом U(r) = —GMomo/r. приводит к тра(?кторіш в(])орме ііскажеішого. но ста工口(еского 'Эллипса, так что эффекта типа смещения перигелия данные поправки не вызывают. Более интересным оказывается пример, связанный с вышеупомянутой аномалией ускорения космического зонда Пи

онер 10. Радиальное ускорение зонда, записанное в формате ar =

dr dt

dr dr dr dt

d(r²/2) dt '

просто рас

считывается как производная квадрата радиальной скорости, определяемой из интеграла энергии,

ar = Qn

1 +

(P - 4)E - 冬 + 2(P - 4) a + 包 2 丄 2moc²     moc²     moc² r   2c² r²

rje qn = -GMomo/r2 — ньютоновское ускорение. В случае аномалии Пионера целесообразно учитывать только те релятивистские добавки к ускорению, которые убывают не быстрее чем qn，то есть в (формуле (36) следует оцепить только п(?рвы(? дв(? постоянны*? поправки. По данным НАСА [17], на расстоянии rp = 6 • 1014 см от Солнца зонд Пионер 10 имел скорость Vp = 1, 5 • 106 см/с： ігзв(?стііы также масса Со л іш, a Ms = 1,99 • 1033 г ii в(? личина гра.вптатііі-оііііой постоянной G = 6, 67 • 10-8 см3г-1 с-2. Это позволяет вычислить классическое ускорение зонда aN = -GMs/гр = —3, 7 • 10-4 см/с2 и вклад механической энергии зонда в первую поправку E/(m°c2) — 10-9. В тіелом первая поправка имеет порядок — 10-13 см/с2 что на，5 порядков меньше значения наблюдаемой аномалии.

Вторая поправка определяется постоянной Uo, которую можно трактовать как локально постоянную (фоновую) гравитационную энергию части Галактики (включающей гало), расположенной в квазисферической области радиуса солнечной орбиты R — 10²² см и имею щей массу M g — 1045 г [19]. Такого рода фоновая гравитация приводит к дополнительному (помимо ньютоновского) замедлению космического зонда

QG = — QN---7

m0 c2

GMG aN Rm0c2

= — 0, 44 • 10^-8 с м/с²,

что сравнимо с наблюдаемой величиной «аномалии Пионера», которая (не исключено) может являться суммой влияния различных физических факторов.

6.    Заключение

Завершая на этом статью о кватернионной модели теории относительности, следует сказать следующее. Здесь не только изложены физико-математические основы построения данной теории, но, как представляется, также продемонстрированы и определенные практические выгоды ее использования для решения широкого спектра кинематических и динамических задач механики. Однако эта практичная теория не может считаться завершенной с чисто математических позиций, поскольку в ней системы отсчета представлены триадами кватернионных векторов, базовыми единицами алгебры, но не элементарными математическими объектами. Такими объектами, как показано в работе [2], являются спиноры, составляющие диады на фундаментальной поверхности, и нет сомнения в том, что все основные соотношения векторной теории относительности также могут быть записаны в терминах кватернионных спиноров. Но эта задача пока еще ждет своего решения.