Фрагильность халькогенидных и оптических стекол

Стеклообразные материалы в настоящем вызывают довольно большой интерес в качестве функциональных материалов. В связи с этим в процессе увеличения количества известных составов стекол появилась необходимость в их классификации. Принято считать, что одним из наиболее удачных является деление стекол по их хрупкости. Для этого вводится понятие фрагильности, которая описана в широком перечне научных работ и определяется как коэффициент наклона графика зависимости логарифма вязкости lg η от отношения ( T g /T ) при температуре стеклования T g [1-3]. Относительно недавно к изучению фрагильности сте- 19

кол вновь повысился интерес. Толчком к этому послужили опубликованные Новиковым в 2000-х годах интересные работы, характеризующие стеклообразные системы с новой стороны [4]. В частности, им были получены данные о связи упругих модулей с характеристикой нелинейности силы межатомной связи, т. е. параметром Грюнайзена.

Фрагильность, как уже упоминалось, определяет, насколько быстро падает значение вязкости при увеличении температуры расплава, следовательно, значение фрагильности можно найти при помощи анализа графиков зависимости логарифма вязкости от отношения температуры стеклования к температуре расплава в области, близкой к значению первой температуры [1; 5]:

a ig( 7 )

m =----- d (Tg/T )

,

T = T g

По хрупкости стекла в первую очередь делят на хрупкие и нехрупкие. По доступным и распространенным данным о температурной зависимости вязкости легко рассчитать значения фрагильности и таким образом условно разделить образцы на два этих больших класса веществ. Далее, полученные результаты применяются для использования в промышленности и других сферах, где стекло играет важную роль как материал с заданными свойствами.

Работа посвящена методике вычисления m по известным данным о вязкости для бескислородных стеклообразных систем, а также для оптических стекол. Осуществлена попытка установления связи отношения упругих модулей K / G и величиной m для указанных халькогенидных систем.

Способы расчета величины m

В первую очередь стоит обратить внимание на простой метод вычисления величины фрагильности на графиках зависимости логарифма вязкости от отношения температур T g /T .

Для этого необходимо знать лишь табличные данные о температурной зависимости вязкости исследуемых составов в области температуры стеклования. При этом в классической литературе принято считать, что стеклование происходит примерно в одном диапазоне, когда логарифм вязкости равен П ( T g ) = 10¹³ ( Пз ). Соответственно, за температуру стеклования принимается температура, соответствующая данному значению вязкости.

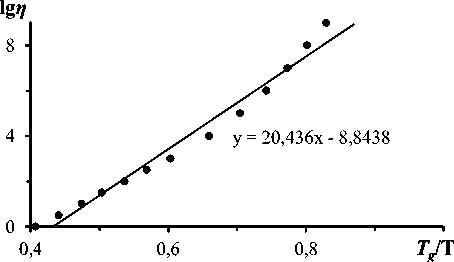
Рис. 1. Определение фрагильности для оптического стекла К8 с применением метода наименьших квадратов, m = 20,4

На рис. 1 продемонстрирован графический способ определения фрагильности для оптического стекла К8. Аппроксимация экспериментальных точек производится методом наименьших квадратов.

Далее, для получения числовых значений параметра m возможно произвести следующие преобразования.

Среди достаточного количества различных уравнений для определения температурной зависимости вязкости, пожалуй, стоит выделить уравнение Вильямса — Ландела — Ферри (ВЛФ), которое благодаря своей конструкции довольно удачно в расчете различных параметров стеклообразных веществ в области стеклования.

Уравнение ВЛФ

lg aT =- C-----g—

содержит две эмпирические постоянные: безразмерную С 1 и имеющую размерность температуры С 2 . Параметр a_T в данном уравнении есть относительная вязкость, равная отношению вязкости системы при температуре стеклования к вязкости при заданной температуре.

С учетом расшифровки относительной вязкости уравнение ВЛФ (2) преобразовывается следующим образом:

T - T

•

g 2

Далее, с заменой переменной в уравнении (3):

T

X = —

T переписываем второе слагаемое уравнения в следующем виде:

—

- C ₁

t - Tg

C1T 1

T 1

I T)

T - Tg + C2

^T I ¹

T g

C,1 + —

T T )

- Cx (1 - x) T c1 - X + -^ • C2

TT

-

-1 (1 - x)

- C1 (1 - X )

1 - X + x -2

I T )

где С = С ₂ / T g •

Уравнение (3) с учетом преобразований:

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА.

Дифференциал d (lg η ) / dx тогда имеет вид:

d ( lg n )__г ¹

—

C 1 (1 — x )   '/

— C1/ dx        1 — x (1

d ig n = c    1

dx Х=1    4 —1(1 — C)

Возвращая замененные переменные, получаем:

d 1g n     =Cl= c, dVTJT) Tg—1 C (C2/Tg )

T

Итак, выбор уравнения ВЛФ с эмпирическими параметрами C 1 и C 2 позволил получить простое выражение для расчета фрагильности

m —

C 1 T g

Параметры уравнения ВЛФ также с большой надежностью можно получить из данных о вязкости при различных температурах.

Параметры халькогенидных стекол в области стеклования

Таблица 1

Состав стекла, мол.%			T g , С	m		m (5)
As	S	Tl
40.00	60.00	-	172		17.4	15.3
36.90	57.93	5.17	134		22.4	18.5
33.90	55.93	10.17	128		23.2	22.9
32.26	54.84	12.90	120		21.0	21.2
31.06	54.04	14.91	115		22.8	20.9
28.17	52.11	19.72	107		23.3	22.3
25.00	50.00	25.00	94		24.9	22.9
P	Se	Te
10.00	90.00	-	55		47.8	46.8
8.00	72.00	20.00	75		46.3	46.4
7.00	63.03	29.97	72		48.0	49.2
6.00	53.99	40.01	72		48.7	46.0
20.00	80.00	-	65		48.7	49.7
18.02	72.07	9.91	77		38.2	35.0
12.00	48.02	39.98	90		35.7	38.2
28.57	71.43	-	78		33.8	31.2
25.64	64.10	10.26	84		37.4	34.0
22.88	57.21	19.91	92		37.4	35.6
17.15	42.88	39.97	76		44.3	43.6
40.00	60.00	-	87		30.9	34.2
35.97	53.96	10.07	88		31.4	27.7

Sb	Ge	Se
10	10	80	118	31.5	36.8
5	15	80	135	27.7	33.7
10	15	75	149	30.6	34.6
20	10	70	151	33.0	33.1
15	15	70	172	30.9	35.9
20	15	65	216	33.3	41.3
10	25	65	305	31.9	35.5
16	20	64	275	35.0	42.5
25	15	60	228	37.7	42.0
20	20	60	244	35.9	40.4
15	25	60	250	37.3	39.2
10	30	60	284	33.0	38.3
AsSe	TlSe	-
100.00	-		162	35.1	39.5
90.00	10.00		136	38.5	35.4
66.60	33.40		121	37.2	39.4
40.00	60.00		69	51.2	53.0

Таблица 2

Расчет фрагильности оптических стекол

Стекло	T g , °С	m	m (5)
К8	741	20.4	23.9
К14	748	18.6	23.3
БК4	751	19.8	20.3
БК10	774	20.2	25.8
ТК20	836	26.6	29.8
БФ11	809	24.2	26.9
БФ12	703	21.0	20.6
ЛФ9	689	20.8	22.9
ТФ1	643	18.2	18.9
ОФ1	658	18.7	18.8

Далее, можно получить выражение, связывающее фрагильность m с температурным интервалом 8 T g , которое, по нашим соображениям, можно рассчитать из данных об эмпирических коэффициентах уравнения ВЛФ. Для составов, характеризующихся схожими свойствами [7], фрагильность имеет значение:

m =

Tg^Tg

Как показывают результаты вычислений в таблицах 1 и 2, формула (5) отражает вполне достоверные значения, соответствующие расчету по выражению (1). δ T_g определяется как интервал температур, в котором происходит переход жидкость — стекло. Численно эта величина по определению равна разности температур при значениях логарифма вязкости 13 и 12 единиц.

Фрагильность и упругие модули аморфных стеклообразных веществ

В настоящее время несомненный интерес вызывает наличие определенной связи параметров линейной теории упругости и различных характеристик стеклообразных систем, не всегда тоже линейных. Одной из таких характеристик является исследуемая в данной работе фрагильность.

Ранее сообщалось, что первые такие работы были проведены Новиковым [4]. Им с соавторами был зафиксирован факт установления прямой зависимости фра-гильности от частного, где в числителе находится модуль объемного сжатия K, а в знаменателе — модуль сдвига G

m

29 — - 0.41

m

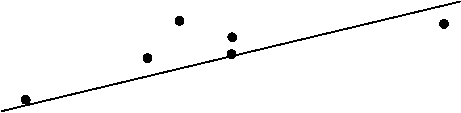
y = 9,9x + 0,1

2,10                  2,50                  2,90 K/G ∙ 10^-8

Рис. 2. Зависимость фрагильности m от величины ( K / G ) для трехкомпонентного стекла As-S-Tl [10]

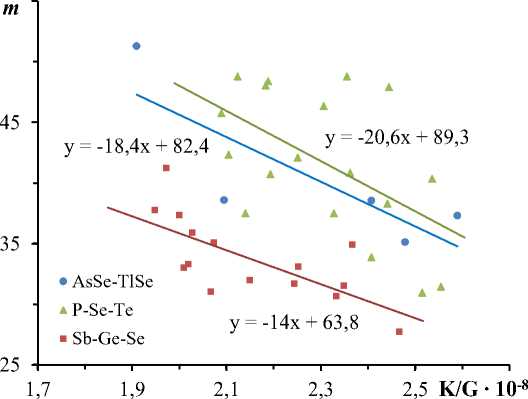
Рис. 3. Графики в координатах m — ( K / G ) для трехкомпонентных стекол по данным о модулях упругости [10]

Согласно классической теории, данное выражение для модулей упругости есть не что иное, как функция коэффициента поперечной деформации μ .

K _ 2 ( 1 + ц G " 3 ( 1 - 2 ц

В связи с этим появляется логичное предположение о том, что хрупкость материала, т. е. его фрагильность, также должна быть однозначно связана с величиной μ .

Коэффициент Пуассона является основным параметром в изменениях сетки твердых стеклообразных веществ [4]. Релаксационные теории стеклования полагают, что хрупкость стекол, которая связана с их вязкостью, в свою очередь, связана с релаксационными процессами и параметрами линейной теории упругости, в том числе с коэффициентом μ .

Релаксация структуры стеклообразного тела протекает с более высокой скоростью, если у данного вещества значительный параметр γ. Это объясняет в какой-то мере, казалось бы, несовместимые параметры m и γ [3; 8; 9].

Нами построены графики в координатах m — K / G для трехкомпонентных бескислородных стекол (рис. 2 и 3). Для состава на рисунке проявляется условно прямая зависимость фрагильности от отношения модулей упругости, но для трех других составов зависимость становится обратная. Предполагаем, что такое различие обусловлено разными динамиками значений коэффициента поперечной деформации в ряду различных процентных соотношений компонентов данных стекол.

Следует отметить, что для исследованных халькогенидных систем формула (6) дает не соответствующие линейным решения. Сложно говорить о линейности графиков, построенных в координатах данной формулы, что, несомненно, требует дальнейших исследований в этом направлении.

Заключение

Анализ двух методов определения фрагильности для халькогенидных и оптических стекол указывает на удовлетворительное согласие. Соотношение параметра m и величины K/G показывает, что для некоторых составов есть определенная линейная корреляция, но для других исследованных стекол такой корреляции нет. Это требует дополнительных расчетов для широкого ряда стеклообразных веществ.