Фрактальные свойства траекторий характерной точки рабочей плоскости плоскодоводочного станка

Как известно [3] основным технологическим оборудованием для финишной обработки поверхностей деталей машин и приборов являются доводочные станки. Кинематические схемы подобного оборудования содержат зубчатые колеса, кривошипно-кулисные механизмы, кулачковокулисные, плоские и пространственные стержневые механизмы, шарнирно-рычажные механизмы, создающие требуемый закон относительного движения притира и заготовки. Методологическая база синтеза подобных механизмов создана в трудах Артоболевского И.И., Тимофеева Б.П., Вей-ца В.Л, Лурье А.И., Бутенина Н.В. и других, где предлагаемые технические решения позволяют получить необходимые сложные и разнообразные траектории характерной точки (ХТ) рабочей плоскости плоскодоводочного станка (РППС), способствующие улучшению качества и производительности доводки [3]

Однако в работах по исследованию процесса абразивной доводки отсутствуют количественные оценки показателя сложности формируемой траектории и дается лишь качественная их характеристика [2]. Также следует отметить, что использование существующих сложных методов синтеза механизмов для обеспечения требуемых траекторий ХТ РППС не всегда эффективно, поскольку синтезируемые механизмы имеют жесткую кинематическую структуру, не позволяющую обеспечить гибкую переналадку технологического процесса .

В определенных случаях при обработке плоских поверхностей из различных материалов более удобно использовать станок, исполнительный механизм которого построен на базе безреверсного двухшарнирного ма-нипулятора [5].

При использовании данной кинематической схемы манипулятора, где путем регулирования закона движения исполнительного механизма по-87

средством приводных двигателей задается соотношение угловых скоростей и направление движения звеньев механизма, получается широкий спектр траекторий ХТ РППС при абразивной доводке. Траектории являются циклоидальными кривыми [6]. Такое техническое решение позволяет снизить материалоемкость и стоимость оборудования, за счет исключения технологически сложных и дорогих элементов, узлов и агрегатов.

1.    Кинематическая схема комплекса

Кинематическая схема предлагаемого комплекса абразивной доводки содержит инструмент-притир 4, вращающийся относительно вертикальной оси-стойки 1 станка, и манипулятор 2, образующих с сепаратором 5 кинематическую пару С - которая относится к парам третьего класса, позволяющему заготовкам 6 установленными в сепараторе вращаться относительно стойки 1 и самоустанавливаться под нагрузкой P для обеспечения параллельности обработки.

Исполнительный механизм модуля, кинематическая схема которого изображена на рис. 1 (вид сбоку) и рис.2 (вид сверху) имеет две степени свободы.

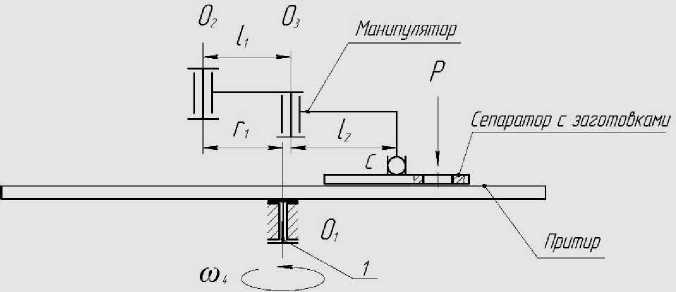
Рис. 1. Кинематическая схема комплекса (вид сбоку) где r 1 - радиус-вектор условного водила (расстояние от стойки притира до стойки манипулятора);

1 1 , 1 2 - длины звеньев манипулятора; P - прилагаемая нагрузка.

На рис. 2 представлен вид сверху кинематической схемы комплекса с заготовками в сепараторе в текущий момент времени в процессе обработки. Сочетание характера движения притира-инструмента, сепаратора с заготовками, их геометрических параметров, соотношения угловых скоростей определяют траекторию, скорости и ускорения ХТ. Двухшарнирный манипулятор позволяет осуществлять гибкую перенастройку траектории [5]. Инструмент-притир вращается с угловой скоростью ю₄ относительно стойки модуля.

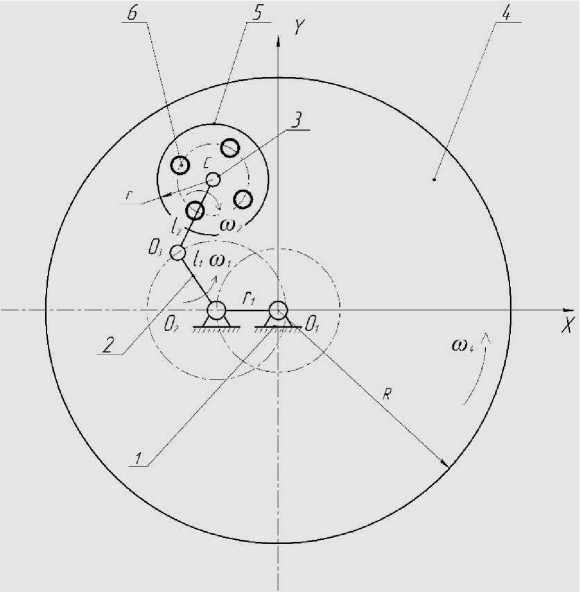
Рис. 2. Кинематическая схема комплекса в процессе обработки (вид сверху)

где ω 4 – угловая скорость притира; ω 1 – угловая скорость 1 звена манипулятора; ω 2 – угловая скорость 2 звена манипулятора.

2.    Расчетная схема

Манипулятор шарнирно связан с сепаратором с обрабатываемыми деталями, находящиеся в трибологическом взаимодействии с притиром. На рис.3, представлена расчетная схема для определения функции положения ХТ принадлежащей поверхности обрабатываемой детали. Вводится прямоугольная система координат O 1 XY , где О 1 – центр стойки модуля, О 2,3 – оси вращения звеньев манипулятора, С – центр сепаратора, М i (X i ,Y i ) – положение произвольно выбранной точки.

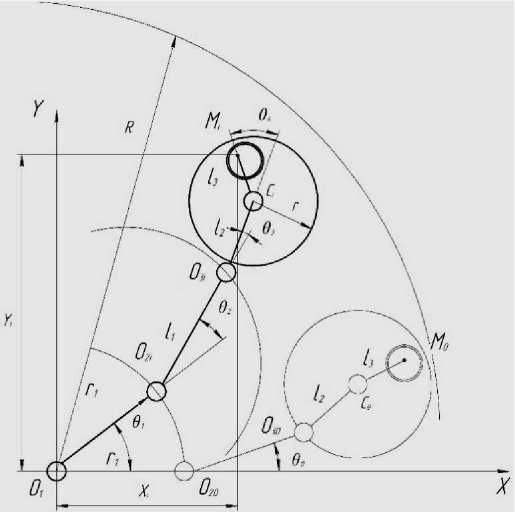
Рис. 3. Расчетная схема определения функции положения исследуемой точки

Координаты точки М следуют из (1):

' X M = r , cos( 9 , ) + 1 , cos( 9 , + 9 2) + 1 2 cos( 9 , + 9 2 + 9 3) +

+ 1 3 cos( 9 , + 9 2 + 9 3 + 9 4 )

Y M = r , sin( 9 , ) + 1 , sin( 9 , + 9 2) + 1 2 sin( 9 , + 9 2 + 9 3) +

+ 1 3 sin( 9 , + 9 2 + 9 3 + 9 4 )

• 9 ,    = to r j t ; 9 2 = ro _r j t + to , t ; 9 3 = to r , t + to , t + m 2 1 ;                               (1)

94 = tor, t + to, t + to2t + toMt; roM = n(ro41 - to21)

где η – коэффициент трения между поверхностью притира и обрабатываемой деталью; ω r1 =-ω 4 – угловая скорость условного водила r 1 относительно притира 4 (рис.2); ω M – относительная угловая скорость условного звена l 3 (расстояние от центра сепаратора до ХТ).

Введем следующие параметры: k=ω 1 /ω 4 и N=ω 2 /ω 1 . Следовательно, уравнения положения исследуемой точки М в относительном движении по притиру выражены системой:

X M = r , cos( - to ₄ 1 ) + 1 , cos( to ₄ 1 ( k - ,)) + 1 2 cos( to ₄ 1 ( k + Nk - ,)) +

+ 1 3 cos( to ₄ 1 ( n + k + Nk - N q k — ,))

Y M = r , sin( - to ₄ 1 ) + 1 , sin( to ₄ 1 ( k - ,)) + 1 2 sin( to ₄ 1 • ( k + Nk - ,)) +

+ 1 3 sin( to ₄ 1( n + k + Nk - N n k - ,))

3.    Траектории характерной точки

Произведен расчет траекторий ХТ М при различных значениях коэффициентов k и N и постоянной угловой скорости инструмента-притира с использованием программного пакета математических и инженерных расчетов Scilab . При моделировании использовалось значение коэффициента трения η =0,75. Траектории ХТ для некоторых параметров k и N даны в таблице 1.

Таблица 1

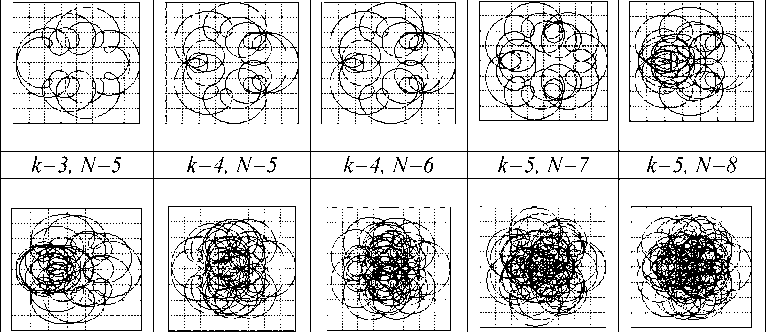
Представленные в таблице 1 траектории имеют различную плотность сетки следов обработки, выбор и управление видом ХТ позволяет формировать необходимые эксплуатационные свойства микрорельефа обработанной поверхности.

4.    Фрактальные свойства траекторий

Как отмечалось ранее в работах по исследованию процесса абразивной доводки более сложная траектория ХТ благоприятно влияет на качество обработанной поверхности. Однако существующая оценка сложности траектории не позволяет провести численную оценку характера.

В данной работе предлагается использовать в качестве количественной оценки сложности ХТ фрактальную размерность [7,8]. Основоположником теории фракталов является Бенуа Мандельброт (1924-2010), предложивший термин фрактал для описания самоподобных математических структур [4]. Фрактальная геометрия изучает закономерности, проявляемые в структуре природных объектов, процессов и явлений, обладающих явно выраженной фрагментарностью, изломанностью и искривленностью. В природе, математике, физике, материаловедении и других областях знаний существует множество объектов и явлений, описание которых эффективно моделируется определенного рода степенным законом [4,7,8].

Характерной особенностью фрактальной геометрии является понятие дробной размерности, в некоторых случаях показывающей насколько плотно точки заполняют пространство. Степенным закономерностям подчиняются и некоторые математические кривые, например, полициклои-дальные траектории мехатронных манипуляционных систем [6].

Для исследования фрактальных свойств некоторых из рабочих траекторий, представленных в табл.1 расчертим плоскость на ячейки, размер которой условно равен a . Далее, уменьшая размер а подсчитаем, сколько ячеек пересекает рабочая траектория. Причем N и а связаны формулой Мандельброта-Ричадсона [1]:

N = Ca - D (3)

где D - искомая фрактальная размерность, C - типичный во фрактальной геометрии неопределенный множитель. Фрактальная размерность рассчитывалась для траекторий с параметрами: 1) k=5, N=7; 2) k=2, N=5; 3) k=3, N=4 ; 4) k=3, N=5 .

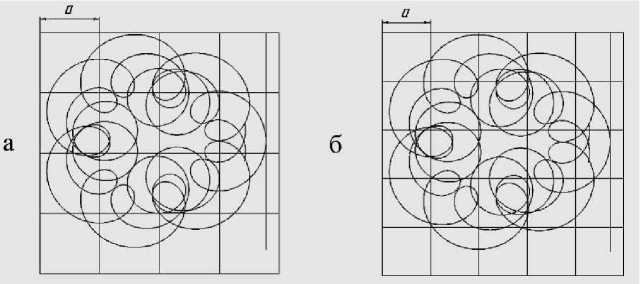
Рис. 4. Пример подсчета числа клеток, содержащих линию а) размер ячейки (условно) а=50;

число клеток, через которые проходит линия N=16;

б) размер ячейки (условно) а=40;

число клеток, через которые проходит линия N=23;

Результаты измерений зависимости числа клеток, в которых располагаются линии траектории, от размера сетки приведены в таблице 2. Там же вычислены их логарифмы.

Таблица 2

Параметры механизма	Размер сетки, а	50	40	30	20
k=5, N=7	Число клеток, N	16	19	34	59
	y=lnN	2,8	3	3,5	4,1
	x=lna	3,9	3,7	3,4	3,0
k=3, N=4	Число клеток, N	15	22	35	74
	y=lnN	2,7	3,1	3,5	4,3
	x=lna	3,9	3,7	3,4	3,0
k=2, N=5	Число клеток, N	14	20	35	50
	y=lnN	2,6	3,0	3,5	4,2
	x=lna	3,9	3,7	3,4	3,0
k=3, N=5	Число клеток, N	16	23	38	77
	y=lnN	2,8	3,1	3,6	4,3
	x=lna	3,9	3,7	3,4	3,0

Наличие фрактальных свойств следует из линейности зависимости lnN от lnA , где N – количество покрытий, а A – масштаб измерения. Из рис. 5 видно, что все точки измеренных траекторий лежат вдоль прямой, значит, зависимость y от x можно аппроксимировать уравнением:

y = c-Dx(4)

Причем, коэффициент D согласно формуле (3) является фрактальной размерностью.

Просуммируем все измеренные значения y и x :

∑ y = nc - D∑ x(5)

где n – число измерений, в нашем случае n =4.

Затем умножим (4) на x и полученное выражение снова просуммируем:

∑xy=c∑x-D∑x2

Теперь (5) умножим на Σx, а (6) на n. От полученных обоих выражений возьмем разность друг от друга, а разрешим относительно D. В итоге по- лучим:

У у = 2,8 + 3 + 3,5 + 4,1 = 13,4;

У х ² = 15,21 + 13,69 + 11,56 + 9 = 49,46;

У ху = 10,92 + 11,1 + 11,9 + 12,3 = 46,22;

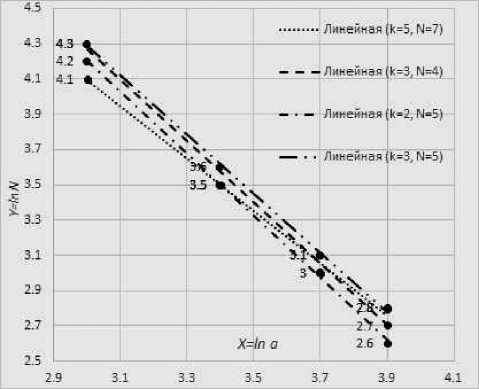
Рис. 5. График зависимости, определяющей фрактальную размерность, в двойном логарифмическом масштабе

Подставляя все известные величины в (5), находим, что для заданного вида движения ( k=5, N=7 ), фрактальная размерность равна:

D = 14-13,4-4^ = 478.

4 . 49,46 - 14²

Аналогичным образом находятся фрактальные размерности для рабочих траекторий механизма с другими параметрами:

D =1,435 при k=2, N=5 ; D =1,674 при k=3, N=5 ; D =1,739 при k=3, N=4 .

Заключение

Предлагаемая конструктивная схема мехатронного комплекса абразивной доводки обеспечивает сложные и разнообразные рабочие траектории путем комбинации вращательных движений и их кратности по отношению к вращению притира. ХТ имеют фрактальную размерность, которую можно использовать как классификационный признак сложности. Таким образом, используя данный классификационный признак можно на этапе синтеза механизма оценивать характер получаемого движения, а на этапе технологического проектирования обоснованно выбирать закон управления рабочим движением для обеспечения заданного качества обработки. Однако последнее, требует экспериментального подтверждения на опытной установке.