FSM Circuits Design for Approximate String Matching in Hardware Based Network Intrusion Detection Systems

Published Online December 2013 in MECS DOI: 10.5815/ijitcs.2014.01.08

Content matching is a process of finding a predefined patterns of string character in an a-priori unknown input stream. Content matching is the most often used option at modern Intrusion Detection and Prevention Systems (NIDPS) like Snort [1] . The content keyword used in Snort allows to a user an important feature to set a rule that search for a pattern in the package payload and based on that process to raise an alarm or reaction. On high speed network searching for all the content option throughout all the incoming and outgoing packages is a resource excusing process that is slowing down the performances of the system. More over there is a need to perform a check to a possible variations of the content because of so named "evasion" techniques. Software systems have processing limitations in that regards. On the other hand hardware platforms, like FPGA offer efficient implementation for high speed network traffic.

Excluding the regular expressions as special case ,the problem of approximate content matching basically is a k-differentiate problem of finding a content C = c1 c2....cm in a string T = t1t2 tn such as the distance D(C,X) of content C and all the occurrences of a substring X is less or equal to k , where k < m < n . The approximate content matching with k mismatches i.e. the minimal number of substitutions to change one content to another with same length is named Hamming distance. The Levenshtein distance or edit distance is a string metric of minimal number of character edits (insertion, deletion and substitution) required to change one word to another not necessarily equal lengths. A non-reduced NFA circuit for Levensthein distance matching with (m+1)(k+1) states have been presented by [2]  . The Damerau-Levensthein distance or generalized Levenshtein distance is used to refer do the edit distance including transposition of any two adjacent characters in a pattern. We will present sequential logical circuits for real time approximate content matching including character alternation, substitution, insertion, deletion and transposition. The approach presented in this paper is based on the theory of [3] and [4] . The rest of the paper is organized as follow: section 2 gives a brief review of the related work in the scope and the basic principles used in this research. Section 3 describes formal definition of Final State Machines (FSM).

The implementation of generalized Levenshtein approximate content matching as an "upgraded" solution of [2] and extended with the concept of complexity reduction is presented in section 3.1. Tending to reduce the required memory elements we present the solution as DFA is section 3.2. The benefits and trade-offs compared to relate work are concluded in section 4 and 6.

• II.    Background

In the recent years there have been several studies for content matching in hardware mostly implemented on FPGA's. The three main design approaches are bruteforce, NFA and DFA. The brute-force approaches [5] [6] are efficient designs for high speed networks but mostly intended for exact content findings. Approximate matching could be achieved upon too much wasted programmable logic resources and in that manner it is impractical for complex patterns. The first to use non-deterministic finite automata (NFA) on a programmable hardware for regular expressions are the authors of [7] . They have used technique of so called One-Hot-Encoding (OHE) scheme. At OHE each state is represented by a flip-flop where active state is represented by 1 and inactive by 0. Based on this research an efficient design for complex pattern matching including bounded-length wildcard and approximate content matching using NFA circuits have been presented by [8] . The same paper has introduced a 8-to-256  shared ASCII character decoder. The deterministic automata (DFA) approach uses a state machine to track pattern matches across clock cycles. By definition DFA can have only one active state but that beneficially yields to a compact state encoding.

• III.    FSM Circuits

Content matching and approximate content matching is basically a sequential problem and therefore in hardware it can be solved using sequential logical circuits. Formal definition of FSM explains it as a seven - tuple

M = ( Σ , Ψ , Q , δ , λ , s , F ) , where

E - Is the input alphabet;

T - Denotes the output alphabet;

Q- Is the finite set of states;

• δ : Q × Σ → Q - is the next state function;

• λ : Q → Ψ - represents the output function;

s ∈ Q - The initial state;

• F ⊂ Q - set of final states;

Each FSM has a finite number of states of which one is initial state. At each unit of time FSM accepts a letter from input alphabet, in our case the whole set of ASCII characters, which cause a translation from one state to another. The movement across the states is defined by the next state function 5. In some states FSM produces an output letter defined by the output function. The concept of our solution is based on Moore type machine shown on Fig.1

Next state function

memory state

Output function

Fig. 1: Block diagram of Moore FSM

Since package inspection is performed on the payload (layer 5-7 of OSI model) the input alphabet E is defined over all set of ASCII characters. The simplest character decoder is presented by 8-to-1 bit decoder i.e. eight port logical AND port as shown on Fig. 2

А comparator

Fig. 2: Simple 8-to-1 decoder (comparator)

In the same manner an alternation function can be presented as simple OR logical port. Alternation between two characters encompasses approximate matching with equal uncertainty i.e. equal probability to occur one of the two possible characters. Techniques of evasion most often use the principle of character alternation replacing lower case with upper case characters or visually similar alphanumerical characters, for example S → 5 , B → b, b → 6, I → ! etc.

• 3.1    Non-Deterministic Finite Automata

NFA representation is a directed graph where each node is a state and each edge is associated with a input character. A nondeterministic machine can have such transition in which a state could be activated without input character. These transitions are so called ԑ-transitions. Additionally, from each state of NFA it is allowed more than one edge to originate for the same input character, yielding a NFA to have more than one active  states. In context of  approximate content matching NFA's transition diagrams are appropriate for pattern finding simulation. For the purposes of this paper let M be a non-deterministic finite automata M recognizing the language of contents L(M) = {C ,C } and all variants of C1 and C2 where C1 ="ABC " , C2 ="AbC". M = (X,Q,5,s,Fk) having that I is the

ASCII set, s is the initial state, Q = { q_Y , q₂ q_n } , 5 is the mapping function and F_k = { F ₀, F ₁..} is a set of final state , where index k represents the number of errors allowed. Ψ = {0,1} is omitted from the formulation of M .

Obviously C ₁ and C ₂ mismatch in the second character ( c ↔ c ′ ) and therefore an alternation function B|b can be used.

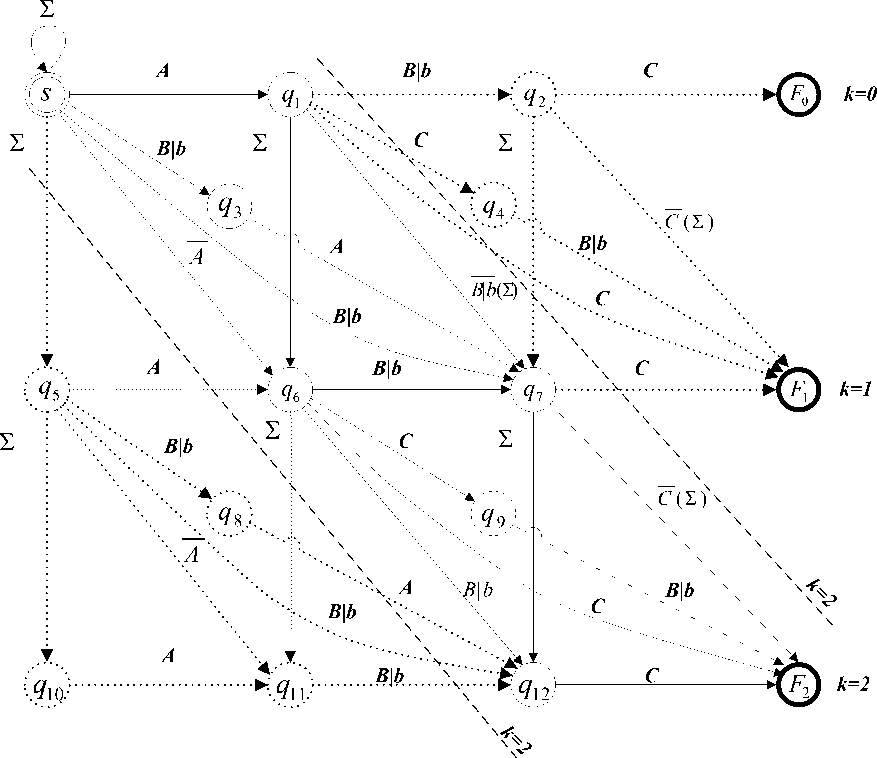
Fig. 3.1.1: NFA transition diagram for generalized Levenshtein approximate content matching with 2 errors allowed (k=2) and complexity reduction

Fig. 3.1.1 shows two errors allowed ( k =2) NFA for generalized Levenshtein approximate content matching without ԑ -transitions eliminated using an ε - CLOSURE ( q ) algorithm.

Here A , B and C represent the complementary characters of A,B and C meaning A =Σ- { A }, B =Σ- { B } and C =Σ- { C }.

• 3.1.1    Complexity reduction

• 3.1.2    NFA circuits for approximate string matching

The NFA presented on Fig. 3.1.1 has (m+1)(k+1) + (m-1)k number of states, where m is the length of the pattern and k is the number of errors allowed. There are situations where only the events of mismatches are important but not the number of mismatches occurred. According to [4] in such cases the number of states for generalized Levenshtein approximate content matching could be reduced by cutting the upper right angle triangle from NFA transition diagram thus reducing the graph for k2 number of states. In similar manner we can remove all the states and transition intended to insert a character before the content to be find and it's associate states. Thus the overall reduction of states is given by

2 k ² (1)

It is obvious that the reduced number of states is independent of the length of the pattern m, taking in consideration that k <  m . Reducing the number or states retreats important feature - the exact matching. A possible compromise could be acquired by cutting only the down left corner of the transition diagram.

As it was mentioned before the one-hot-encoding (OHE) technique is very suitable to represent the states of non-deterministic finite automata. Each state is associate with a flip-flop in a scheme that the output of a state flip-flop is connected to a input logic to successive one or more than one flip-flops in a logical conjunction depending of the transition edges. Each active state is represented by a flip-flop output 1 and inactive output 0, considering that more or even all the state could be active in the same time. Pattern matching starts with any input character from 2 at the initial state (s) and translates to the one of the final states (F) according to the matching algorithm. A match is registered when there is a liner - time transition including insertion, deletion, substitution and transposition of 1's throughout the flip-flop starting at the initial state and ending at the final state. This is similar process as described by the Shift-And algorithm by [9] . In general NFA for generalized Levensthein approximate content matching requires (m+1)(k+1) + (m-1)k basic memory elements, the same as the number of states. Hence any state of the transition diagram is represented by a most basic memory element, in this case a D flip-flop. In the logical circuit we present as a generalized Levenshtein distance including the size reduction the number of states i.e. the number of necessary flip-flops is equal to

2k(m — k) + m + 1, k < m (2)

NFA implementation in hardware is a feasible solution since multi-active states can be realized as concurrent logical elements. For a given content C="A(B|b)C" a logical circuit for generalized -Levenshtein approximate content matching whose transition diagram was shown in Fig. 3.1.1 in RTL schematic view including character decoders (comparators) is presented on Fig. 3.1.2.

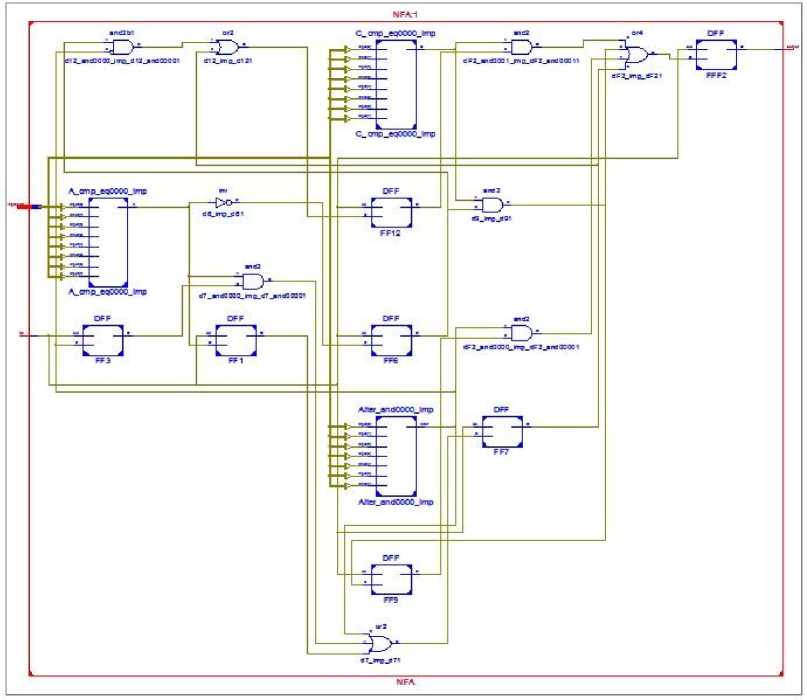
Fig. 3.1.2: NFA logical circuit for generalized Levenshtein approximate content matching from Fig.3.1.1

For simulation purposes ISE Project Navigator (0.61xd) is used. The mapping function 5 i.e. the next state function is a combinational logical circuit composed of basic AND, OR and NOT functions. It is anticipated that all the logical components are synchronized with a centralized clock signal. It is also important to note that the complexity to the input of any flip-flop in the diagram is not more than 5- input OR gate meaning one input for each edit distance metric: exact, insert, delete, replace and transpose, regardless of the overall number of states.

Character comparators (decoders) are presented as well. The mapping function 5 i.e. the next state function is a combinational logical circuit composed of basic AND, OR and NOT functions. It is anticipated that all the logical components are synchronized with a centralized clock signal. It is also important to note that the complexity to the input of any flip-flop is not more than 5- input OR gate meaning one input for each edit distance metric: exact, insert, delete, replace and transpose.

• 3.2    Deterministic Finite State Machines

• 3.2.1    NFA to DFA

• 3.2.2    DFA Circuits for approximate string matching

If the space complexity of a given NFA for approximate content matching is given by mk than the corresponding DFA will have much lower states than 2mk , in fact according [11] this number of states is mk+1. Our intention in implementation of finite state machine for approximate content matching is circuit design with minimal number of memory elements for memory state encoding and minimal complexity of next state and the output function. DFA despite NFA cannot have more than one active state in a given moment of time. But this feature can be an advantage in possibility to utilize the technique of compact or sequential state encoding. In theory the number of bit required i.e. the number of basic memory elements - D flip flops to encode a DFA is equal to log2(mk+1) and still processing input characters in a linear time.

Deterministic finite state automata can be observed as a special case of nondeterministic automata. Consequently, the language accepted by NFA could be accepted by DFA as well. In other words if a language is accepted by NFA given as M = { X , Q, s , 5 , F } we can find a DFA defined by M = { X , Q ', s ', 5 ', F '} that accepts same language, that is L ( M ) = L ( M ') . The transition from non-deterministic automata to an equivalent deterministic automata is performed by mapping all active states in given point of time from NFA to a corresponding singular state of DFA. The last can be mathematically depicted as

5 '( q 01 , A ) = 5 ( q 0 , A ) о 5 ( q 1 , A ) = { s\ }

Table 1 shows mapping from NFA to a equivalent DFA states for transition diagram represented on Fig.3.1.1. Following the concept presented on Table 1 it is feasible to design a pseudo-adaptive DFA like one that do not accepts successive metric of same type. For example from DFA state s0 it can be temporally assumed that the NFA mapping 5 ( q₆ , B | b ) = q_{v 2} is not valid thus removing double character replacement, but the same is yet regular for the others NFA to DFA mappings.

Table 1: NFA to DFA states mapping for transition diagram on Fig.3.1.1

	A	B|b	C	X- { A , B | b, C}
s {s0}	sq 1	sq 3 q 6 q 7	sq 6	sq 6
sq 1 {s1}	sq 1 q 6 q 7	sq 3 q 6 q 7	sq 6 q 7	sq 6 q 7
sq 6 {s2}	sq 1 q 12	sq 3 q 6 q 7	sq 6 q 9 q 12 F 2	sq 6 q 12
sq 1 q 12 {s3}	sq 1 q 6 q 7	sq 3 q 6 q 7	sq 6 q 7 F 2	sq 6 q 7
sq 6 q 12 {s4}	sq 1 q 12	sq 3 q 6 q 7	sq 6 q 9 q 12 F 2	sq 6 q 9 q 12 F
sq 6 q 7 {s5}	sq 1 q 7 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 9 q 12 F 2	sq 6 q 12 F 2
sq 6 q 12 {s6}	sq 6 q 12	sq 3 q 6 q 7	sq 6 q 9 F 2	sq 6 q 12
sq 1 q 6 q 7 {s7}	sq 1 q 6 q 7 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 7 q 9 q 12 F 2	sq 6 q 7 q 12 F 2
sq 1 q 7 q 12 {s8}	sq 1 q 6 q 7 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 7 q 12 F 2	sq 6 q 7 q 12 F 2
sq 3 q 6 q 7 {s9}	sq 1 q 7 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 9 q 12 F 2	sq 6 q 12 F 2
sq 6 q 9 q 12 {s10}	sq 1 q 12	sq 3 q 6 q 7 F 2	sq 6 q 9 q 12 F 2	sq 1 q 12
sq 6 q 7 q 12 {s11}	sq 1 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 9 q 12 F 2	sq 6 q 12 F 2
sq 1 q 6 q 7 q 12 {s12}	sq 1 q 6 q 7 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 7 q 9 q 12 F 2	sq 6 q 7 q 12 F 2
sq 3 q 6 q 7 q 12 {s13}	sq 1 q 7 q 12	sq 3 q 6 q 7 q 12 F 2	sq 6 q 9 q 12 F 2	sq 6 q 12 F 2
sq 6 q 7 q 9 q 12 {s14}	sq 1 q 12 F 2	sq 3 q 6 q 7 q 12 F 2	sq 6 q 9 q 12 F 2	sq 6 q 12 F 2

Single active state feature of DFA is favorable condition for compact and natural binary encoding in the synthesis process. If N is the number of states of DFA than the number of required memory elements for encoding the memory state is at most ^ log₂ N ^ + 1 using binary coding. But there is always a trade-off between reduced memory elements and complexity of next state and output function on the other hand. Also, in circuit design views DFA are easier to describe in HDL (hardware description language). Fig. 3.2.1 shows

DFA logic circuit implementation for mapping function presented in Table 1. The realization of DFA circuit performs the same approximate matching of the content "A(B|b)C" as the circuit presented on Fig.3.1.2. It should be noticed that circuit on Fig. 3.2.1 does not incorporate character decoder because of simplicity. As it can be seen only four flip-flops are used to encode each of eight DFA states. The next state and the output function is assembled by combinational logic much complex in term combinational logical elements utilized compared to NFA.

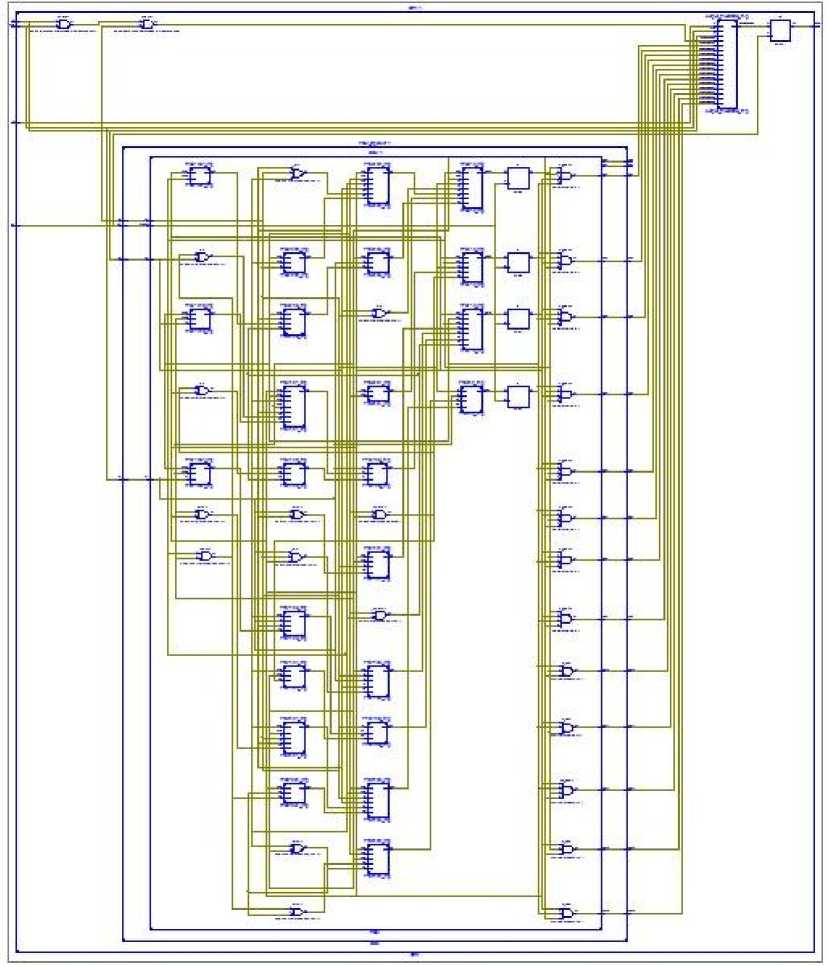
Fig. 3.2.1: DFA logical circuit for generalized Levenshtein approximate content matching from Fig.3.1.1

• IV.    Evaluation Results and Discuss

The FSM logical circuit modules presented here are able to process one input character per clock cycle concurrently regardless of the number of edit distance metrics incorporated. Compared to the exact string matching circuits we achieve the same processing speed but with much more "flexibility".

FSM Circuits Design for Approximate String Matching in Hardware

Based Network Intrusion Detection Systems

The NFA design presented in this paper uses one-hot encoding and therefore the number of memory elements used for memory state is equal to the number of states of transition diagram for approximate content matching. As far as authors are aware the only similar concept for approximate string matching in hardware has been implemented by [2] . Compared to their design have reduced number of states and enhanced performances to detect transposition besides insertion, deletion and substitution. For the DFA design we have implemented classical approach to FSM with binary encoding. The benefit is reduced number of memory elements used to record a state as a trade-off to the complexity of the next state and the output functions. Considering the hardware fundamental features that accept concurrent implementations NFA's are better solutions in that regards.

Compared to exact content matching and regular expression matching approximate matching has some drawbacks. Namely, they are prone to false positives reports. Reducing the complexity i.e. removing the states for exact matching may cause enormous number of approximate detections since in that manner the system is set to function to at most k mismatches. Still the approximate string matching despite regular expression matching provides better control of the number errors allowed.

• V.    Conclusion

In this paper we presented a method to design an approximate content matching module implemented in hardware as a Moore type FSM logical circuit. We have used Damerau-Levenshtein distance theory to enhance the performances of previous proposed designs i.e. to detect switched positions of two neighboring characters in a pattern as one of the methods utilized by evasion techniques. Additionally an alternation function was employed. Both theoretical concept (NFA and DFA) have been coded in HDL and simulated by ISE Project Navigator (0.61xd). The simulated results are meeting the projected criteria of our design. In similar manner principles presented here can be expanded to a more complex matching components e.g. with more than two errors allowed ( k >2) and combination with other complex matching methods .