Функции комплексных переменных с большими параметрами, построение областей

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                       

Постановка задачи. Асимптотическое поведение решений сингулярно возмущенных уравнений сводится к исследовании функций [1-5]

t

F(t o ,t,l) =

t o

t expA(pi(t0,t) - (p1(t0,T))dT,..., J t0

expA(p_n⁽t₀,t) - p_n⁽t₀,T))dT

)

где 0 < A — большой параметр; t₀,t E D ^ C — множество комплексных чисел, a D — односвязная, открытая область; t₀ — фиксирована, t переменная.

Пусть выполняется условие:

У. p j (t₀, t) E Q (D) - пространство аналитических функций в D, j = 1,...,n.

Задача. Определить область D₀ ^ D, где выполняется соотношение

Vt E D₀(^F(t₀, t,A)^ < C 1 — const при A ^ +“),

^F(t₀, t,A)^ = max ^tE D o

I( j ⁽t 0 ,t)l.

Поставленную задачу решим для следующих случаев:

• 1.    p1(t0,t) = (t + i) — (t0 + i)2, p2(t0,t) = 2ln(t + i) — 2ln(t0 +i).

• 2.    (1^0, t) = (t — i) — (t0 — i)2, (2(t0,t) = 2ln(t — i) — 2ln(t0 —i).

• 3.    P 1&0 , t) = ⁽t + i)² — ⁽t 0 + i⁾², ( 2 ⁽t 0 , t) = ⁽t — i)² — ⁽t 0 — i)²,

Фз(^0,^) = 2ln(t + i) — 2ln(t0 + i),p4(t0,t) = 2ln(t — i) — 2ln(t0

Рассмотрим случай 1. Как показывают исследования проведенные в [1-5] если удаётся определить область D₀ и множество П = {(p(t₀, t))}, где (p(t₀, t)) — гладкая или кусочногладкая кривая соединяющая точки t₀,t E D₀ ^ D , причем по кривым (p(t₀,t)) функции Rep j (t₀, t) — не возростают, то выполняется (2).

Таким образом решение задачи сводиться к определению области D₀ и построению множества П.

• 1.    Геометрические построения. Сначала построим область D₀ . Для этого в ведем в рассмотрение функции Rep 11 = t² — (t₂ + 1)²,Rep₂₁ = ln(t 2 + (t₂ + 1)²) и их линии уровня. Точка (0; -1) является точкой перевала для функции Rep 11 . Линия уровня (p₀) = {t E С, Rep 11 = 0 }, проходящая через точку перевала, всю плоскость С разбивает на четыре сектора, причем в каждом из этих секторов Rep 11 принимает либо положительные, либо отрицательные значения. Линии уровня (p) = {t E С, Rep 11 = p Ф 0} являются гиперболами, а линии уровня (q) = {t E C,Rep₂₁ = q} концентрическими окружностьями, с центром в точке (0; -1) (Рисунок 1).

  

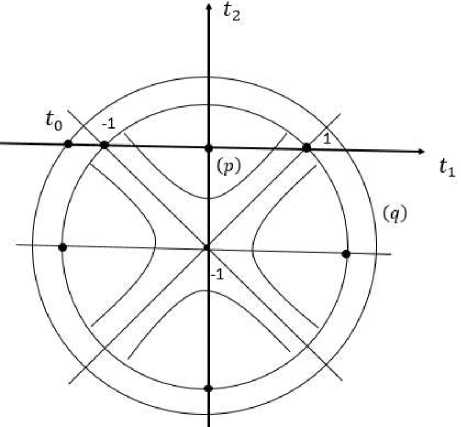
  Рисунок 1. Линии уровня (р) и (q)

  
  

Возьмём t₀ < 1. Тогда окружность ( t 2 + (t₂ + 1)² = г²) проходящая через точку (t₀; 0) имеет радиус г = ^t ^ + 1. Верхнюю часть окружности соединяющую точки (t₀; 0), (1-5; -1+ ^t 0j + 28 — 8² ) обозначим (К 1 ). Найдем уравнение прямой проходяющую через точки (t₀; 0) и (0; -1+5) (0<5 - const не зависящая от в).

Пусть t2 = kt1 + b. Полагая t1 = —t0, t2 = 0, затем t1 = 0,t2 = —1 + 8 находим k иЬ b = —kt0,    k = —

— 8

to   '

тогда t2 =~—(t1 — t0). Часть этой прямой обозначим [(t0; 0); (0; —1 + 8)]. Теперь to проведем прямую t1 = 1 — 8 . Эта прямая с (К1) пересекается в точке (1 — 5; —1 +

^t % + 28 — 8²). Часть пррямой t 1 = 1 — 8 соединяющая точки (1-5;  0);  (1-5;

-

1+V t 02 + 28 — 8²) обозначим [(1 — 5; 0), (1 — 5; —1 + ^t ^ + 28 — 8²) ].

Часть прямой t 1 — t₂ [(0; —1 + 5) и (1 — 5; 0)].

-

5; 0),(1-5;

— 1 + 8 = 0 соединяющая точки (0; -1+5) и (1-5; 0) обозначим Через (К₂) обозначим: [(t₀; 0), (0; —1 + 8)] U [(0; —1 + 5), (1 — —1 + ^t 0 + 28 — 8²)] . Рассмотрим область D₀ ограничченный

(К 1 ) U (К 2 ) (Рисунок 2).

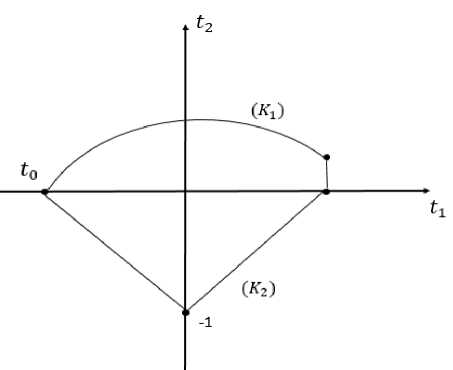
Теперь определим множество Q для Reф₁₁(p(t₀, t)) состоит из части (K 2 ) ^[( t o ,t), ⁽ t i ,t 2 ) ^] и отрезка [(^, ^Ht^)]^^, I2 ) е ^(t^) G D_o)) ; для Re^ 2i (p(t o ,t)) состоит из части (K i )[(t o , 0), (t i , t 2 )] и отрезка [(t₂, ^(t^t^KCt ! , t₂) е K i , (t i ,t 2 ) е D o )) (Рисунок 3).

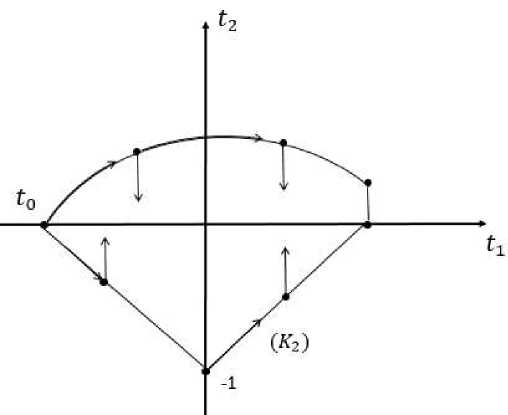
Рисунок 3. Пути (p(t_o, t))

Нетрудно проверить, по выбранным путьям (p(to,t)) функции Re^ii и Re^2i не возрастают.

Теперь рассмотрим случай 2. Заметим функции Re(p_ii = t 2 — (t² + 1) 2 и

Repi2 = t2 — (t2 — 1)2  ; Rep2i = ln(t2 + (t2 + 1)2 и Rep22 = ln(t2 + (t2 — 1)2 в симметричных, относительно действительной оси, точках принимают равные значения.

Тогда возьмём кривые (K_i) и (K₂), которые симметричны, соответственно, к кривым (K_i) и (K 2 ) , относительно действительной оси. Область ограниченный (K_i) и (K 2 ) обозначим (D_o). Для этого случая пути (p(t_o,t)) выбираются симметричными, относительно действительной оси, к путьям (p(t_o,t)). По выбраным путьям функции Re^_i2 и Re^₂₂ не возростают.

• Случай 3. Как и в предыдущих случаях рассмотрим функции

Pii(t) = (t + О2, P2i(t) = (t — О2, p3i(t) = 2ln(t + 0, p4i(t) = 2ln(t — i) и

ReP ii (t) = t 2 — (t² + 1)², Rep 2i (t) = t 2 — (t² — 1)²;

R^eP_3i(t) = ln(t 2 + (t² + 1)², Rep_4i(t) = ln(t 2 + (t² — 1)².

В этом случае сгрупируем рассматриваемые функции. Обьединим Re^_ii(t) с Re^_4i(t), а Re^_2i(t_o,t) с Re^_3i(t_o,t). Покажем один из возможных вариантов определения D_o и Q. Будем считать t_o > V3 и проведем прямую проходящую через точки (—t_o, 0) с угловым коэффициентом k = —1 т.е. t₂ = —(t_i + t_o). Далее проведем прямую (l) t_i —1₂ — 1 + 5 = 0 (0<δ – достаточно малое число не завиящее от ε). Данные прямые пересекаются в точке A i ^(— ₂ ^(t o ^{— 1 + 5) —} 2 ^(t o ^{+ 1 — 5))}

Прямая (l) ось ti пересекает в точке (1 — 5; 0) отрезок [(—to; 0), A2] обозначим (K2), а отрезок [A2, А2] (K2). . Далее определим (K2) и (K2) соответственно симметричные, относительно действительной оси к, (K2) и (K2). Область ограниченный (K2), (K2), (K2) , (K2) возьмём за Do (Рисунок 4).

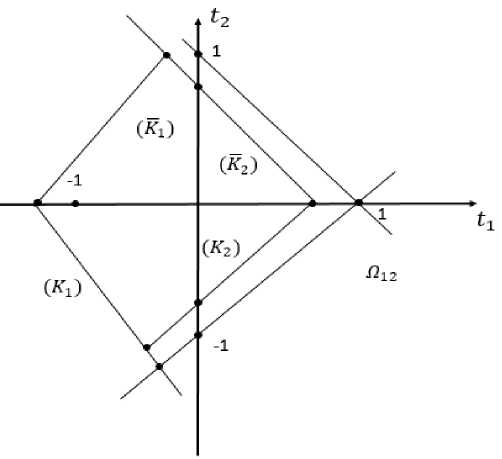
Рисунок 4. Область D₀

Выберем пути интегрирования. Для Re^ 11 (t) и Rep₄₁(t) путь (p(t₀,t)) состоит из части (K 1 ) U (K 2 )[(t₀; 0),t] и отрезка [t = t 1 + it₂,t = t 1 + it₂], а для Re^₂₁(t) и Re^₃₁(t) путь (p(t₀,t)) выбриается, симметричным (относительно действительной оси) к (p(t₀,t)). Нетрудно проверить по (p(t₀,t)) функции Rep 11 (t), Rep₄₁(t), а по (p(t₀, t)) функции Re^₂₁(t), Re^₃₁(t) не возрастают

Выводы

На некоторых примерах функций комплексного переменного показано построение областей и выбор путей интегрирования, которые обеспечивают асимптотическую ограниченность интегралов экспоненциальных функций с большим параметром.