Функция Грина для одной задачи кинематической теории дифракции

В настоящее время в задачах рентгеновской дифракции нередко возникает ситуация, когда на поверхность кристалла падает рентгеновское излучение, состоящее из когерентных пучков. Эти пучки могут быть сформированы путем пропускания плоской рентгеновской волны через систему диафрагм или путем напыления на кристалл решетки из металлических полос [1]. В этом случае падающее на кристалл излучение можно представить как плоскую рентгеновскую волну, промодулированную по амплитуде вдоль входной поверхности кристалла.

Для примера рассмотрим кристалл (рис.1), на который падают два пучка одинаковой ширины.

Рис. 1. Два рентгеновских пучка падают на плоскопараллельную кристаллическую пластинку.

Fig 1. Two x-ray beams fall on a plane-parallel crystal plate.

Излучение рентгеновских пучков будем аппроксимировать плоской волной, амплитуда которой промодулирована функцией с двумя прямоугольными импульсами, показанной на рис. 2.

f (x)

l

x

Рис. 2. Функция, модулирующая плоскую волну.

Fig 2. A function that modulates a plane wave.

В случае N падающих пучков модулирующая функция будет иметь N прямоугольных импульсов. Более того, мы рассмотрим задачу для достаточно произвольной модулирующей функции f ( x ) .

1. Функция Грина для данной задачи

Пусть на плоскопараллельную кристаллическую пластину в точке x = x 0 падает бесконечно узкий луч, т. е. модулирующая функция f ( x ) имеет вид f ( x ) = 5 ( x — x 0 ) . Здесь 5 ( x ) — дельта-функция Дирака. В итоге возникнут отраженные лучи, и картина будет выглядеть так, как это схематично изображено на рис. 3.

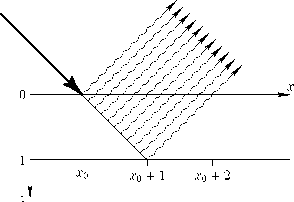
Рис. 3. Падающий на кристалл луч порождает отраженное излучение.

Fig 3. Falling on the crystal generates a beam of reflected radiation.

Запишем уравнения Такаги для данной задачи (в кинематическом приближении)

д Eо + -V dEh _ dEh ∂x ∂z

ai Eo(x,z), b 2 Eo(x, z) + a 2 Eh (x, z), граничные условия

E ₀ ( x, z = 0) = 6 ( x — x ₀ ) ,    E h ( x, z = 1) = 0 .

Уравнения (1) записаны в приведенной системе единиц, в которой единицы длины безразмерны x ^ X" tg 9 B ,     z ^ Z , а параметры a 1 , a ₂ , b 2 име-

Lz                     Lz ют вид iπLz a i = х . п X о, Л sin OB

a 2 = \ ■ z ⁽ X о ^{— а} ) , Л sin o _B

b 2

iπL _z

Л sin 9 _B ^{X g} "

Решение задачи (1) есть

E ₀ ( x, z ) = e ^{a 1 z} 6 ( x — x ₀ — z ) , b 2       a 1 + a 2             a 1 _ a 2

^E h ^{( x},^z ) = ₂ ^ex P (—2— ^{( x _ x} 0) +--2— ^z)

x Ц Т ( x — x 0 — z ) — U ( x — x 0 + z — 2)] .

U ( £ ) —функция Хевисайда, равная нулю при £ <  0 и равная единице при £ >  0 . Тогда для произвольной модулирующей функции f ( x ) для дифрагированной волны имеем решение

E h ^{( x,z} ) = / ^E h ⁽ x ^{— £,}z ) f ^{( £} ) d^£,

-∞

где

Eh (x — £,z) = b2      a1 + a2           a1 — a2

₂ ^exp(—2—⁽ x " ^{£ ) +}—2— z) ^X (5) x [ U ( x — £ — z ) — U ( x — £ + z — 2)]

играет роль функции Грина для данной задачи.

Рассмотрим следующий пример. Пусть модулирующая функция f (x) есть гауссова функция f (x ) = visexp (— ^) ■

Расчет по формуле (4) даёт

Eh(x,z) = bl exp [ (a1 +R‘2)2°2 + 4      L8

a ₁ + a ₂      a ₁ — a ₂

+     2 x +     2

( r ( a 1 + a 2 ) ° 2 + 2( x — z )

x erf  ------—=------- t2V2

( a 1 + a 2) ° ² + 2( x + z — 2) — erf------------—-----------

2V2 °

Здесь функция erf z определена как ^2 = J ^ e t ² dt .

Оказывается, можно ещё более упростить выражение (4). Подставим функцию (5) в интеграл (4) и проинтегрируем по частям, получим

Eh(x,z) = bl exP ( a 1 + a2x + a 1 2 a2z) x x {U(x - £ - z) Ф(£)|   +

-∞

∞

+ J Ф( £ ) 6 ( x - £ - z ) d£ —

-∞

• -    U ( x - £ + z — 2)Ф( £ ) | “ —

  -∞

∞

• —    j Ф( £ ) 6 ( x - £ + z — 2) d£ } .

  -∞

Здесь введено обозначение

Ф( £ ) = I' exp ( — a l ± a 2 £ ) f ( £ ) d£.

Нижний предел в этом интеграле произволен, нам удобно взять его таким. В выражении (7) слагаемые с функцией Хевисайда зануляются. В итоге получим Eh(x, z)=b2 exp (a1 ++a 2 x+a 12 a 2 z)x x {/ exp ( — alP£) f(£) d£ — (8)

-∞ x+z-2

• ^—    j ^e xp ( ^{— a 1 + a 2 £} ) ^{f ( £} ) ^d£ } .

  -∞

• 2. Расчет интенсивности дифрагированной волны

Это выражение более удобно для расчетов дифрагированной волны внутри и на поверхности кристалла.

Как пример использования формулы (8) приведем расчет интенсивности дифрагированной волны для случая, когда на поверхность кристалла падает рентгеновская волна, промодулированная функцией f ( x ) в виде N прямоугольных импульсов.

Рис. 4. Модулирующая функция в виде N прямоугольных импульсов.

Fig 4. Modulating function in the form of N rectangular pulses.

Для начала найдем интенсивность дифрагированной волны для более простого случая: N = 2 (см. рис. 1 и 2). Рассчитаем амплитуду дифрагированной волны, используя формулу (8), подставив в нее f ( x ) в виде двух прямоугольных импульсов. В результате интегрирований получим следующее выражение:

E h ( x, z ) =

^b 2 ------ X a i + a 2

x ( u ( x - z ) в ^{а 1 z [} в ^{( a 1 + a 2 )( x — z} ) / ² - 1^] +

• + U ( x + z — 2) x

x ^ a 1 + a 2 (1 — z ) [1 _- в ( a 1 + ^a 2 )( x + z- 2) / 2 ^] |

+ U ( x — z + U ( x + z

i ) в 1 ^z [i l - 2) x

в (a 1+ a 2)(x — z-l )/ 2] + x в 1+a2(i-z) [в(a 1+a2)(x+z-l—2)/2 i] +

+ U ( x - z - l - d ) e ^{a 1 z [} в ^{( a 1 + a 2 )( x — z — l — d} ) / ² - 1^]

+ U ( x + z - l - d - 2) в ^{а 1 + a 2 (1 — z} ) x

r

в ( a 1 + a 2 )( x + z — l — d— 2) / 2 ] ।

+ U ( x — z x e ^{a 1} z [1

+ U ( x + z

r

r

r

2l - d) x в ( a 1+ a 2)( x — Z — 2 l-d)/ 2] +

2 l - d - 2) e ^{a 1 + a 2 (1} -z ) x

X [ в ⁽ a 1 + a 2 ⁾⁽ x ⁺ z- ^{2 l — d — 2)} / ²    1]}

Это выражение довольно громоздкое, но структура его достаточно проста. Каждая функция Хевисайда U ( £ ) задает внутри сечения кристалла границу, правее которой (т. е. вдоль оси x , см. рис. 1) начинает действовать выражение, на которое умножается соответствующая функция Хевисайда (левее этой границы этот множитель дает нулевой вклад).

Теперь найдем суммарную амплитуду дифрагированной волны (с учетом фазы) на верхней поверхности кристалла по формуле

S ( q x -q z )= /      E h ( x,z

-∞

= 0) в iq x dx.

Здесь верхний предел взят равным 2 l + d + 2 , поскольку при x >  2 l + d + 2 поле в кристалле (в кинематическом приближении) равно нулю.

В результате интегрирования получим

S ( q x ,q z ) = ь 2

exp( a ₁ + a ₂ - 2 iq _x ) - 1 ^iq x ⁽ a 1 ⁺ a 2 ^{- 2} iq x )

в iq x l + в -iq x ⁽ l ^{+ d} ) в -iq x ⁽² l ^{+ d} )

Теперь найдем интенсивность как функцию q x и q z :

I ⁽ q x ,q z ) = IS ⁽ q x ,q z ) 1 ² =

= Ib 2 в ^ia | ² l ²

sin ( a - ( q x + q z ) / 2) ^{2 a - (} q x ⁺ q z ) / ²

x sinn q x l ^ _COs 2 ⁽^L ± d ) , ( q x l/ 2i        ^ ^{2 1}

где a = ( nL _z ) / ( A sin 9 B ) x о - В обычной (неприве-денной) системе единиц это выражение примет вид

I ( q x ,q z ) = Ib 2 ^^aI ² ( l tg 9 b /L z ) ² x

x

sin [ a - ( q x ctg 9 b + q z ) L z / 2] ² a - ( q x ctg 9 b + q z ) L z / 2

x ^Sm2 ^ x l/ ,2) cos ² ( q^l + d ) .

( q x l/ 2) ^{2                 2 J}

Наконец, если f ( x ) имеет вид функции с N прямоугольными импульсами, то суммарная амплитуда дифрагированной волны на верхней поверхности кристалла есть

S ( q x ,q z ) = ь 2

exp( a ₁ + a ₂ - 2 iq x ) - 1 a ₁ + a ₂ - 2 iq _x

+

1 - в-iqxl x-------- iqx

1 _- (> -iq" ( l + d ) N

• 1    — в ^-ii x ⁽ l ^{+ d} ) ,

а интенсивность отражения дифрагированной волны определяется следующим выражением

I ⁽ q x ,q z ) ~

sin ( a - ( q x + q z ) / 2) ^{2 a - (} q x ⁺ q z ) / ²

sin² ( q x 2) sin² ( q xl + d N) ------------------------------------- •   -----------------------------------------------------

⁽ q x 2 ^{) 2}       sin ² ( q xl + d )

Заключение

Мы показали, что использование функции Грина в задачах кинематической теории дифракции значительно упрощает расчет поля дифрагированной волны внутри сечения кристалла в виде плоскопараллельной пластины, на поверхность которой падает рентгеновская волна с амплитудой, меняющейся произвольным образом вдоль латерального направления.