Функция размытия точки четырехволнового преобразователя излучения в многомодовом волноводе с керровской нелинейностью

Интерес к четырехволновому взаимодействию в волноводах обусловлен возможностью реализации в них больших эффективностей преобразования (коэффициентов отражения) за счет увеличения области нелинейного взаимодействия без существенного изменения интенсивностей взаимодействующих волн [1–5].

Использование четырехволновых преобразователей излучения в системах адаптивной оптики, в системах обработки в реальном масштабе времени изображений, временных сигналов [6-9] невозможно без установления соответствия между пространственно-временными характеристиками взаимодействующих волн [10; 11].

В работах [12–15] в приближениях заданного поля по волнам накачки, малого коэффициента отражения с использованием метода функции размытия точки (ФРТ) проанализировано качество обращения волнового фронта (ОВФ) четырехволновыми преобразователями излучения в многомодовых волноводах при использовании сред с различным типом нелинейности, с учетом схемы распространения взаимодействующих волн, пространственной структуры волн накачки. Однако приближение малого коэффициента отражения не позволяет рассмотреть влияние интенсивностей волн накачки на качество обращения волнового фронта.

Целью настоящей работы является исследование качества обращения волнового фронта четырехволновым преобразователем излучения в многомодовых волноводах с керровской нелинейностью при больших коэффициентах отражения, когда необходимо учитывать не только перекачку энергии их волн накачки в сигнальную и объектную волны, но и перекачку энергии из объектной волны в сигнальную и наоборот.

1. Вывод выражения для ФРТ

Расмотрим типичную схему вырожденного четырехволнового взаимодействия to+to-to = to со встречными волнами накачки. На нелинейную среду, расположенную между плоскостями z = 0 и z = / , падают две волны накачки с комплексными амплитудами A i и A 2 и сигнальная волна с комплексной амплитудой A 3 . В результате четырехволнового взаимодействия генерируется объектная волна с комплексной амплитудой A 4 , распространяющаяся навстречу сигнальной волне и имеющая волновой фронт, обращенный по отношению к волновому фронту сигнальной волны (рис. 1).

В приближении заданного поля по волнам накачки, без учета изменения диэлектрической проницаемости среды вследствие самовоздействия, самодифракции волн накачки, система уравнений, описывающая четырехволновое взаимодействие, имеет вид [10]:

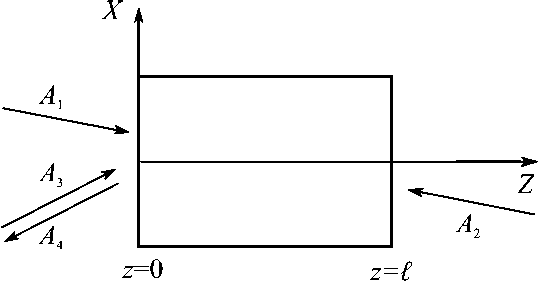
Рис. 1. Схема четырехволнового взаимодействия

Fig. 1. Scheme of four-wave interaction

{ v ² + k ² n ² ( x ) } A 1 2 = 0,

(V ² + k ² n ² ( x )) A = ^{24 ПЮ X} A 1 A 9 A 4 3 3,4           2         1 2 4,3

( 3 )

Здесь x — нелинейная восприимчивость; n ( x ) -показатель преломления; k to / c ; to - циклическая частота; c – скорость света в вакууме.

Пусть четырехволновое взаимодействие реализуется в волноводе. Разложим амплитуды взаимодействующих волн по модам волновода:

N

A1 (x, z) = Z aln (z)fn (x) exp(—iPnz) ’ n=0

N

^A 3 ( x , z ) = Z a 3 s ( z ) f ( x ) ^eXP ( — i ^P s z ) , s = 0

N

A 2 ( ^X ’ z ) = Z a 1 m ( z ) ^fm ( x ) ^eXP ( i ^P m z ) ’ m = 0

N

A 4 ( x , z ) = Z a 4 r ( z ) ^fr ( x ) exP ( i ^P r z ) - r = 0

Здесь a jn ( z ) - коэффициенты в разложении амплитуд взаимодействующих волн по модам волновода; f n ( x ) - n -я мода волновода; в n - постоянная распространения n -й моды; j = 1,4; N - число отсечки.

С учетом (2) в приближении медленно меняющихся амплитуд система уравнений (1) примет вид da ln = 0, da im = 0.

dz dz da3s =-i ^2п®2X(3) x dz          c2вs

NNN x Z ZZalna2ma4rYnmsr eXP(—'Anmsrz)’ n=0 m=0 r=0

da 4 _r = . 12nto ² x⁽ 3 ) ^dz c ² p _r

x

NNN x Z ZZ alna 2 ma 3 s Ynmsr eXP (-iA nmsrz ), n=0 m=0 r=0

^где Y nmsr = J f n ( ^x ) f m ( ^x ) f ( ^x ) f ( ^x ) ^{dx -} интеграл перекрытия, ^A nmsr = ^p n — ^P m — ^P s ^{+ P} r -

Рассмотрим четырехволновое взаимодействие в длинном волноводе ( A nmsr £ » 1, A nmsr * 0). Если волны накачки одномодовые с равными номерами мод A i 2 ( x, z ) = a i2 _n exp ( + i p n z ) , то из условия синхронизма вытекает, что r -я мода объектной волны однозначно связана с r -й модой сигнальной волны.

От системы связанных уравнений для коэффициентов в разложении амплитуд сигнальной и объектной волн по модам волновода (3) можно перейти к дифференциальным уравнениям второго порядка:

d a 3,4 r     2

—7Y” + Gnra 3,4 r = 0- dz2

Здесь

_ 12 nto ² x⁽ 3 )        ( 0 ) ( 0 )

Gnr       2л     Ynnrra1 n a2n ’ c 2P r a1 n )= a1 n ( z = 0 ), a 2n)= a 2 n ( z = £ ).

При выполнении граничных условий a 3 s ( z = 0 ) = a 3°?, a 4 r ( z = £ ) = 0

значение коэффициентов в разложении амплитуды объектной волны по модам волновода на передней грани нелинейного слоя есть a4г (z = 0 ) = -ia3°)* tg (Gnr £) -

Если четырехволновое взаимодействие реали- зуется в кольцевом резонаторе, осуществляющем обратную связь по сигнальной и объектной волнам, то граничные условия на коэффициенты a3s и a4r имеют вид [16; 17]

a3s ( z = 0 ) = 71 R1a3s^ + 7R1R2 a3s ( z = £ ), a 4 r ( z = £ ) = 7R1R2 a 4 r ( z = 0 ) -

Здесь R ₁ - коэффициент отражения полупрозрачного зеркала связи; R ₂ - коэффициент отражения зеркал, осуществляющих перенос амплитуд сигнальной и объектной волн с одной грани волновода на другую.

С учетом граничных условий (7) значение коэффициентов в разложении амплитуды объектной волны по модам волновода на передней грани нелинейного слоя есть a 4 r (z = 0) = - i J1 — R1 x

a 30 ^sin ( G nr ^£ )

[ 1 + R 1 R 2 ] cos ( G nr £ ) - 2 ,^’2'

^Y nnrr

1 1 3, если r = n , 4 a 1 2, если r ^ n .

При R 1 = R 2 = 0 из выражения (8) получается выражение (6).

В качестве сигнальной волны возьмем волну от точечного источника, расположенного на передней грани нелинейного слоя в точке с координатой x 0 ( A 3 ( x , z = 0) = § ( x - x 0 ) ) . Зная выражения для коэффициентов в разложении амплитуды объектной волны по модам волновода, найдем выражение для ФРТ на передней грани волновода:

Г (x, x 0, z = 0) = - i1 - R1 x x у    f (x)fr (x0 )sin (Gnr£)                     (9)

^{X Z} [ 1 + ^R 1 ^R 2 ] cos ( G nr ^£ ) - ² ^RR'

При отсутствии обратной связи по сигнальной и объектной волнам выражение для ФРТ примет вид

N

^Г 1 ( x , x 0 , z = ⁰ ) = ^- i Z ^fr ⁽ x ) ^{f (} x 0 ) tg ⁽ G nr ^£ ) .        ⁽¹⁰⁾

r = 0

Выражения (9), (10) полностью описывают качество преобразования излучения при четырехволновом взаимодействии в многомодовом волноводе с керровской нелинейностью при наличии (9) и отсутсивии (10) обратной связи по объектной и сигнальной волнам.

При выполнении граничных условий (5) первая точка «генерации» наблюдается при условии

G nn ^£ = ^П  ^

®2x( 3 )£ a (0) a (0)= ± c2 ka 1 n 2 n    18.

Вторая точка «генерации» наблюдается при ус-

ловии

G £= - nr 2

^

® ² х^{( 3 ) £} a ( 0 ) a ( 0 ) = J_ c ² ka ¹ n ² n 12.

2. Анализ результатов

При выполнении условий

[ 1 + R 1 R 2 ] cos ( G nr £ ) - 2 ^RR = 0

коэффициент r -й моды в выражении для ФРТ (8) стремится к бесконечности (точка «генерации»), именно эта мода и будет определять вид ФРТ.

В случае отсутствия обратной связи по объектной и сигнальной волнам условие «генерации» (11) перепишется следующим образом:

cos ( G nr £ ) = 0. (12)

Если в качестве волновода используется волновод с бесконечно проводящими поверхностями, расположенными на расстоянии 2 a , то модами такого волновода являются функции [18]:

При записи условий (15), (16) считали, что вид ФРТ определяют приосевые моды волновода ( в _r - k ) [14]. Условия (15) и (16) позволяют при известных параметрах волновода с бесконечно проводящими стенками, значении нелинейной восприимчивости найти интенсивности волн накачки, при которых реализуются условия «генерации».

Вблизи первой точки «генерации» вид ФРТ определяет мода волновода, номер которой равен номеру мод волн накачки.

Вблизи второй точки «генерации» вклад в выражения для ФРТ моды волновода, номер которой совпадает с номером мод волн накачки, пренебрежимо мал. С увеличением числа приосевых мод, учитываемых при расчете ФРТ, отсутствие одной моды в выражениях (9) и (10) слабо сказывается на виде ФРТ. Таким образом, вблизи второй точки «генерации» четырехволновой преобразователь излучения осуществляет преобразование сигнальной волны с высоким качеством и большим коэффициентом отражения.

Наличие двух точек «генерации» при четырехволновом взаимодействии в волноводе с беско-

нечно проводящими поверхностями предполагает наличие в выражении для ФРТ моды, номер которой равен номеру мод волн накачки. Если это условие не выполняется (например, рассматривается функция размытия точки, расположенной

f n ( ^x ) = "Т ^sin a

п ( n + 1 )

x

2 a

Интеграл перекрытия мод волновода с беско-

нечно проводящими поверхностями есть

на оси волновода, и номер мод волн накачки нечетный), то для этой точки существует одна точка «генерации», определяемая выражением (16).

Рассмотрим в качестве волновода параболический волновод б ( x ) = n ² [1 - 2 S 2 ( x I x q ) ² ], модами которого являются функции Гаусса – Эрмита [18]:

•w fn(x) =

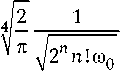
H n

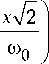
r exp

® 0 ,

Здесь

в

г

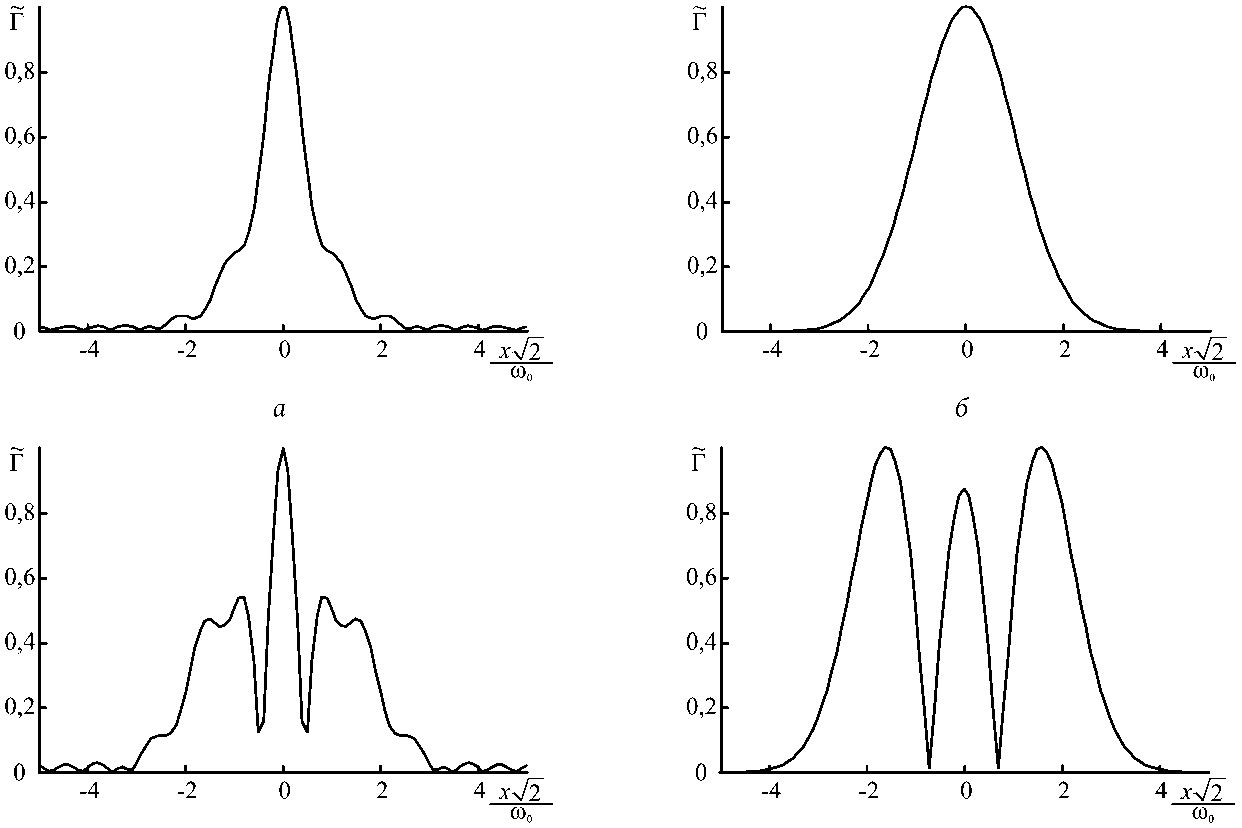
Рис. 2. Зависимость модуля ФРТ от поперечной координаты при к ® о = 20, N 1 = 20, n = 0, G ₀ = 10 ³ ( а ), 1,57 ( б - первая точка «генерации»), 3 ( в ), 4,19 ( г – вторая точка «генерации»)

Fig. 2. Dependence of the PSF modulus on the transverse coordinate at к о ₀ = 20, N 1 = 20, n = 0, G 0 = 10 ^{- 3} ( a ), 1,57 ( b - the first «genera-tion» point), 3 ( c ), 4,19 ( d is the second point of «generation»)

Hn

O,

– функция Эрмита n -го порядка,

^O 0 =

² x q

k ^2 ^ 2

.

С учетом (17) выражение для ФРТ (10) примет вид

N ₁

^Г 2 ^{( x} , x 0 , z = ⁰) = - Ч _П £ —— ^x r = 0 ^{2 r} • ^O 0

x H r

x 0 ^²

^O 0

H r

x V 2

^O 0 J

exp

—

^{x 2} + ^{x 2} "

« 0 ,

tg ( G nr t ) .

Вид ФРТ существенным образом зависит от интеграла перекрытия. Подробный анализ интеграла перекрытия четырех мод параболического волновода приведен в работе [12]. Интеграл перекрытия у _nnrr имеет максимум при n = r . По мере увеличения разности между номерами мод |n - r | значение интеграла перекрытия монотонно уменьшается.

На рис. 2 приведены характерные графики нормированного модуля ФРТ четырехволнового

преобразователя излучения ( Г = Г ( x , x = 0, z = Gy /Г    , Г - наибольшее значение модуля

,max ,max

ФРТ) при различных значениях нормированной интенсивности волн накачки

_     12 по ² х⁽ 3 ) t         ( 0 ) ( 0 )

^G 0 =      Т      ^Y 0000 ^a1 n a 2 n •

I           c ² k                  J

Как и при четырехволновом взаимодействии в волноводе с бесконечно проводящими поверхностями, при четырехволновом взаимодействии в параболическом волноводе для волн накачки с номерами мод n = 0,2,6,... первая точка «генерации» наблюдается при совпадении номера моды объектной волны с номером мод волн накачки (рис. 2, б ). Вблизи этой точки «генерации» вид ФРТ определяет мода волновода, номер которой совпадает с номером мод волн накачки.

Уменьшение с увеличением номера мод волн накачки значения интеграла перекрытия у nnnn приводит к росту интенсивности волн накачки, при которых реализуется условие «генерации».

В отличие от четырехволнового преобразователя излучения в волноводе с бесконечно проводящими поверхностями, для четырехволнового

преобразователя излучения в параболическом волноводе число точек «генерации» равно числу мод, учитываемых при нахождении ФРТ. Вблизи этих точек «генерации» вид ФРТ определяет одна мода волновода с номером r ^ n (рис. 2, г ).

На рис. 3 для волн накачки с номером моды n = 0 приведена зависимость полуширины центрального максимума ФРТ ( A x ), определяемая из уравнения

|г ₂ ( x = ^A x , x = 0, _Z = 0 ) = 1 r ₂ ,_max ,                  (19)

от нормированной интенсивности волн накачки. По мере приближения интенсивности волн накачки к интенсивности, при которой реализуется условие наблюдения первой точки «генерации», полуширина модуля ФРТ увеличивается, что свидетельствует об ухудшении качества преобразования излучения. При дальнейшем увеличении интенсивности волн накачки ( G о >  1.7 ) основная доля энергии изображения точечного сигнала перестает быть сосредоточена в центральном максимуме (рис. 2, в ), что не позволяет использовать значение A x для оценки качества ОВФ.

Учет наличия положительной обратной связи по объектной и сигнальной волнам без изменения вида ФРТ значительно снижает значения интенсивностей волн накачки, при которых реализуется условие «генерации»:

G nr £ = arccos

Г„ ТТ"^А ²У R 1 R 2

1 + RR

V ¹² 7

Так, например, при параметрах кольцевого резонатора Ri = 0,5, R2 = 0,8 значения интенсивности волн накачки, при котором наблюдается первая точка «генерации» при четырехволновом взаимодействии в волноводе с бесконечно про-

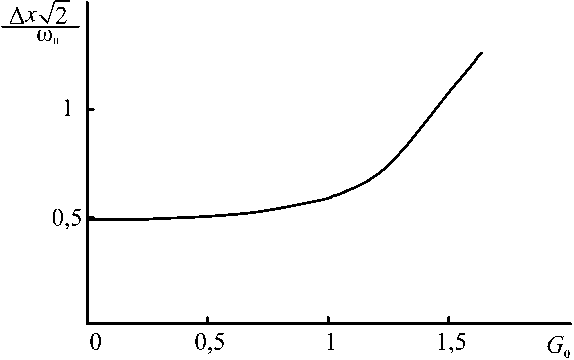
Рис. 3. Зависимость полуширины модуля функции размытия точки от интенсивности при к ® о = 20, N 1 = 20

Fig. 3. Dependence of the half-width of the modulus of the point blur function on the intensity at к ® o = 20, N 1 = 20

водящими поверхностями, оказывается в 3 раза меньше, чем при отсутствии обратной связи по объектной и сигнальной волнам.

Заключение

Учет перекачки энергии из сигнальной волны в объектную и наоборот при четырехволновом взаимодействии в волноводе с керровской нелинейностью при одномодовых волнах накачки приводит к появлению точек «генерации», в которых коэффициент отражения стремится к бесконечности. Найдены условия на параметры волновода, волн накачки, при которых реализуется условие «генерации». Вблизи первой точки «генерации» вид ФРТ определяет мода волновода, номер которой совпадает с номером мод волн накачки.

Наличие положительной обратной связи на сигнальную и объектную волны без изменения вида ФРТ приводит к значительному уменьшению значения интенсивностей волн накачки, при которых реализуется условие «генерации».