Функция влияния вариационной задачи

В работе покажем возможность превращения интуитивного физического подхода, к понятию функции влияния в математически точное понятие. Базисом этого преобразования физического понятия в математическое послужил вариационный принцип физики, являющийся одной из главных физических аксиом. На основе точного описания потенциальной энергии, соответствующей виртуальному состоянию исследуемой системы, минимизация

«Московский физико-технический институт (национальный исследовательский университет)», 2023

этого функционала энергии позволила получить главное математическое описание функции влияния Н (ж, £) в виде уравнения

IР^НЦх, №^ж = h(«,

Γ где Ы(ж) - произвольное значение функционального параметра из класса допустимых функций, а интеграл по Г понимается как сумма интегралов по всем ребрам нашей сети. Это уравнение оказывается отправной точкой для доказательства всех важнейших свойств функции влияния.

Геометрическим графом (пространственной сетью) называется совокупность ребер -открытых интервалов yt = (at, at) из R” вида yt = (at, a't) = {ж : ж = at + At (at - at), 0 < А < 1}, точки at и at естественно называть концами yt.

Некоторое множество А таких концов объединяем с множеством всех точек Ut(at,at), и обозначим это объединение через Г. Точки a Е А, являющиеся концами объединяемых интервалов, называются внутренними вершинами, если такие точки оказываются общими для двух интервалов. Такие вершины называются узлами. Их множество обозначаем через J (Г). Разные интервалы у t и у^ по определению не пересекаются и могут только смыкаться в общих узлах. Объединение U yt всех ребер мы обозначаем через Н(Г) Таким образом, Г = Д(Г) U J (Г).

Наряду с внутренними вершинами, т. е. узлами из J(Г), нам необходимо выделить остальные концы - вершины интервалов yt из -Й(Г), которые не вошли в Г. Мы будем называть эти вершины граничными, а их множество обозначать через д Г.

2.    Определение функции влияния

Пусть изучаемая реальная система, состояние которой описывается скалярнозначной функцией «(ж), находится под действием закона наименьшего действия. Это состояние есть состояние объекта, порожденное внешней нагрузкой F . Мы считаем, что F - это функция множества, определяемая так: если П - некоторое подмножество Г, то F (П) - вся внешняя нагрузка, приложенная именно на это множество П. Если нагрузка сосредоточена в некоторой точке, а П - множество, состоящее из этой точки: П = {£}, то J и(ж)еІҒ = «(£)/(£).

Ω

Пусть потенциальная энергия этой системы, соответствующая виртуальному состоянию «(ж), определяется интегралом

V («(ж)) = У - У udF,                            (1)

где Г - некоторый koi ючный граф из R³.

Функцией влияния Н^ (ж) описанной системы называется минималь функционала

/ 2

—^ж -«(£).                              ( 2)

Γ

Этот последний функционал отличается от предыдущего тем, что второе слагаемое не имеет привычного интегрального вида, но может определяться дифференциалом Стильтьеса с единичным атомом меры. Физический смысл второго слагаемого очевиден - оно означает работу, выполненную единичной силой на дистанции «(£). Поэтому физический смысл минимали (2) - реальная форма, принятая системой под воздействием приложенной в точке ж = £ единичной силы. Здесь, как и всюду далее, мы будем через Е обозначать множество физически допустимых функций, которые должны

• •    быть определены на Г,

• •    быть непрерывны на Г, включая все внутренние узлы,

• •    иметь почти всюду на ребрах Г обычную производную - иначе формулы (1) и (2) лишаются смысла.

3.    Главное свойство функции влияния

Мы допускаем, что в граничных узлах (из дГ) имеются какие-либо дополнительные условия - глухого закрепления, упругих реакций, линейного взаимодействия с какой-либо другой линейной системой - для нее это не важно. Так же, как пока неважно, где наши реальные формы имеют вторую производную. Функцию влияния Н (ф), зависящую пока от ф как от параметра, мы будем обозначать через Н (ж, ф), «поднимая авторитет ф», ибо далее выяснится главенствующая в некоторых вопросах роль этого параметра ф

Теорема 1. Для того чтобы определенная на Г х Г функция Н(ж, ф) била функцией влияния нашей задачи, необходимо и достаточно, чтобы для функции и(ж) = Н(ж, ф) выполнялось на каждой һ(ж) из Е тождество j pu'h'dx = һ(ф).                                       (3)

Γ

Доказательство очевидно - тождество (3) есть уравнение Лагранжа, которому Н (ж, ф) должна удовлетворять по ж.

Теорема 1 описывает условия, необходимые и достаточные для определения функции влияния. Именно поэтому при всей внешней простоте она будет играть в дальнейшем фундаментальную роль.

Мы пока интересуемся чисто внешними физически важными свойствами функции влияния, поэтому некоторые более глубокие с математической точки зрения вопросы (например, вопрос о существовании функции влияния) мы откладываем на потом.

Теорема 2. Пусть Н (ж, ф) - функция влияния нашей задачи. Пусть Дж) - заданная на Г интенсивность внешней нагрузки. Тогда состояние нашего объекта определяется формулой

^и(ж) = ja ^(ж,ф)/^(ф Ж                           (4)

Покажем, что функция (4) удовлетворяет уравнению Лагранжа:

j риДДж — j hf dж = 0, h Е Е,                      (5)

соответствующему функционалу (2). Здесь f(ж) - интенсивность, заданная по условию. Так как функция Н (ж, ф) - минималь функционала (3), то эта функция должна удовлетворять соответствующему уравнению Лагранжа, т. е. тождеству

/р(ж)—Щ h(ж)dж = һ(ф), dЖ где һ(.) - любая допустимая функция из Е. Умножая последнее тождество (при любой һ Е Е) на исходную интенсивность f(ф) внешней нагрузки (беря у f (.) в качестве аргумента переменную ф. получаем

Фиксируя произвольную һ(.), мы видим, что равенство справедливо для всех £. Проинтегрируем его по £:

j (j Р(х)Н'х(х^Цх^сҚ = j h(E,)f (ОсҚ.(7)

Γ

Если в левом интеграле изменить порядок интегрирования, то мы получим

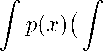
Γ

Н‘(x,Of (eWWW = j h(Of (eW,(8)

причем внутренний интеграл в точности равен, согласно соотношению (5):

u(x) = l Н'х(^Of (0)de.(9)

Γ

А поэтому (4) удовлетворяет, в силу (7), уравнению Лагранжа, что и доказывает теорему. В рамках инженерной математики проведенная аргументация считается более чем удовлетворительной. Однако мы занимаемся не физическим, а математическим моделированием, и поэтому обязаны показать правомочность изменения порядка интегрирования в (7) и право перехода от (7) к (8). Для этого нам потребуется установить ряд глубоких математических свойств функции Н (x, £) и ее производной Н'_х (x, £). Но это нам удается сделать лишь по мере того, как мы сможем доказать существование функции влияния, найдя ей при этом какое-либо явное представление, удобное для анализа.

• 4.    Свойства функции влияния, обусловленные уравнением Лагранжа

Здесь мы исходим из того, что функция Н(x,) двух переменных, определенная на Г х Г, является функцией влияния исходной задачи тогда и только тогда, когда для любой допустимой һ(х) Е Е справедливо тождество j p(x)Н,х(x,e)O(x)dx = h(e), һ Е Е.

(Ю)

Предложение 1. Пусть £о _ какая-либо точка из Г и у - ребро Г, не содержащее £q. Тогда ііа. у p(x)—Н7(x, ^о) = const.(11)

Для доказательства рассмотрим допустимые функции h(x) на Е такие, которые отличны от нуля только на одном ребре у . Тогда интеграл по Г, трактуемый как сумма интегралов по ребрам, превратится в один обычный интеграл по ребру у:

pu'h'dx = 0.(12)

Значение h(£) справа в (10) оказывается нулевым, поскольку e Е У • Преобразуя (12) к виду pu'dh = 0, һ Е Е,(13)

мы имеем, в силу классических результатов теории интеграла Стильтьеса, что pU = const на у. Опираться на теорию [3] интеграла Римана - Стильтьеса мы имеем полное право, так как һ непрерывная, a pU имеет наверняка ограниченную вариацию.

Итак, не зная заранее ничего о существовании второй производной у Н(x,s) по x, мы уже обнаружили, что Н(x,s) удовлетворяет по переменной x (на интервале у, не содержащем s) уравнению

(pu‘) = 0.

Предложение 2. Для каждой внутренней вершины о G J (Г) при любом sq € Г все сходящиеся к этой вершине у € Г(о) сужения Н⁷(ж, sq) имеют одинаковое предельное значение Н⁷(о, sq) (мы, как это принято, обозначаем через Г(о) совокупность ребер, примыкающих к узлу о).

Доказательство вытекает из предположения о том, что функция влияния при каждом ф принадлежит допустимому классу функций по ж, т.е. должна автоматически быть непрерывной по ж на в сом Г.

Пусть у = (о, Ь) - какой-либо интервал из R” и у(ж) - заданная на у скалярная функция. Считая окрестность точки о, параметризованной в направлении «от о», обозначим производную у (ж) по ж в тонко о. вычисленную в такой параметризации. через у‘(о + 0).

Предложение 3. Пусть ф - точка из Г и о - один из внутренних узлов Г (т. е. о G J (Г)), отличный от ф Тогда функция у (ж) = Н (ж, ф) удовлетворяет следующему равенству:

^ Р7 ^(о>7^{(о + 0)}=^0,                           (До)

7GrM где р7(ж) л у7(ж) означают■ сужения р и у на ребро у.

Для доказательства возьмем в R” такую окрестность П точки о, которая не содержит больше точек из J (Г). Мы можем сузить эту окрестность так, чтобы пересечение каждого ребра из Г е П было связным. Обозначим через Го пересс'чешіе Г е П. Очевидно. Г есть пучок с единственной вершиной о. Обозначим через Е множество всех допустимых (из Е) функций, равных на Г нулю вне П. Тогда для любой такой функции h G E q

^^ j р₇Н'₇ (ж, ф)h‘(ж)dж = 0,                              (16)

где сумма берется по всем ребрам подграфа Го. Заменяя (при параметризации «от а») h^,(ж')dж на. dh II интегрируя по частям, а. затем пользуясь равенствами h|^dr = 0 и тем. что dрH ‘ = const (предложение 1) на каждом ребре, это приведет (16) к равенству

Р7(о)Н7(о + 0, ф)һ7(о) = 0,                                (17)

аналогичному (15).

Предложение 4. Если о - одна из внутренних вершин Г, то в ней должно быть

^ Р7^(о)у7^{(о + 0)} = ^-1,                             (¹⁸>

7GrW где у (ж) = Н (ж, о).

Пусть П - окрестысість тонки о. не содержащаяі других узлов Г. и Го - аналогичный предыдущему граф. Отличие от предыдущего только в том, что из уравнения Лагранжа на соответствующих функциях һ(ж) из Eq мы вместо (15) получим

Р7 (о)Н7 (о + 0,ф)һ7 (о) = -Н (ф).                            (19)

Как следствие, в любой внутренней точке жо € Г, отличной от внутреннего узла (т.е. жо G J (Г) ), функция р(ж)Н‘(ж, ф) имеет по ж единичный скачок.

5.    Заключение

В статье разработан систематический подход, основанный на описании сетеподобной системы математической моделью с опорой на понятие функции влияния. С этой целью дано корректное определение функции влияния, адекватное классическим физическим представлениям. А именно, предположение, что состояние реальной системы описывается вариационным принципом, т.е. минималью энергетического функционала, функция влияния Н(х, £) определена как минималь этого функционала, соответствующая единичному внешнему усилию, сосредоточенному в точке x = £ . Именно такой подход обеспечивает адекватность введенного понятия функции влияния классическим физическим представлениям.

В работе показано главное свойство функции влияния - способность определять реальное состояние объекта в интегральном виде:

n(x) = j Н(x,s~)f (s)ds,                                (20)

установлено адекватное описание функции влияния в виде решения интегрального функционального уравнения pH ‘(x,£)h‘dx = Һ(О,                                 (21)

Γ описанного при любом значении функционального параметра h(x) из класса допустимых возмущений. Именно это последнее свойство, равносильное физическому определению функции влияния, становится ключевым в анализе самых разнообразных математических свойств. Главное достоинство этого чисто математического описания состоит в том, что сетеподобная структура в виде графа Г спрятана внутрь объекта (она не выпячена наружу). Единственное напоминание здесь о сетеобразной структуре - это область интегрирования Г, причем и интеграл понимается как сумма обычных одномерных интегралов Римана (или Лебега) по ребрам графа Г. На базе (21) установлена серия важнейших для математического внедрения свойств функции влияния.