Fuzzy Agent Oriented Software Effort Estimate with COCOMO

Published Online July 2015 in MECS DOI: 10.5815/ijisa.2015.08.03

In the early days of working with computer, software costs made up a small percentage of the total cost of computer systems and So the error in estimating the cost of software, Had relatively little impact. Today software is the most expensive component of any computer system, For example, in custom systems, a large error in the estimated effort costs can be as the difference between profit and loss. Excessive costs would be catastrophic for the software manufacturer.

The estimated cost and work will never be an accurate knowledge. Numerous variables - human, technical, environmental, political, can affect the final cost of the software and the work done to develop it. But, software project effort estimation can be made from a black art to a series of systematic steps that provide estimates with acceptable risk. Software project estimation is a form of problem solving and in most cases, an issue which must be resolved (ie software project cost estimation and users) is more complicated than it needed to pay it all at once. Therefore, we analyze the problem, and bring it into a series of smaller, more manageable issues and we use the various models and factors in any model to estimate the cost.

Some methods such as empirical models is used to estimate software cost, the most famous of them are COCOMO models. But there are many other models like putnam. These models do experiments on previous achievements to predict the same outcome cost .by the help of the cost of these tests, managers of software has estimated the costs,explanation of variables resemble the programmers expertise` s Average, complexity of issues, lines of source code, records and accept other things [1].

Bohm suggested the original COCOMO model which have been Changed in the years to achieve a better result for the calculation of the estimated software cost. Currently, the developed method, is considered COCOMO2, we use this method in this article to estimate the costs.

according to the type of software in different methodologies such as traditional, object-oriented, aspect-oriented, agent-oriented, different factors is being used to estimate the cost, Which we use the agent-oriented software method in this paper. In COCOMO 2, main element which affects the final costs is the size that evaluates the expressed results in sloc or ufp [1]. we use the sloc logic for Agent oriented projects used in this article.

sloc is influenced by several factors in its determination. a lot of work has been done to calculate the sloc value to reach the appropriate PM.

In this paper, we first talk about agent-oriented software and its emerging .

Then we pay attention to these three projects:P815, p907,PSI3 that have been considered in paper[1] as the base of the work and offer some explanations about concepts and performance of COCOMO 2, and finally by making fuzzy the obtained information with COCOMO 2, for the three projects, we are trying to estimate more accurately the cost of an agent-oriented software.

The paper is organized in five sections. After the introduction Section I, Section II which also introduces the related works of agent oriented software cost estimate . Section II continues with agent and COCOMO definition in section III .

In section IV fuzzy models for proposed system and examples presented . Section V and VI presents the results, conclusions of the research. The paper ends with a list of references.

• II.    Literature

Nancy merco in seminar [5] defines the emergence of cost estimation software. She focuses on the analysis of COCOMO 1, COCOMO 2, and Effective and required items in cost estimation by the COCOMO and counts the disadvantages and defects of this method. He believes that, by adding the experimental results to this model the efficiency can be increased and ultimately According to the existing problems in COCOMO 2,he permits to use it in the fields of software project management.

Majed alyahya in [7], first has tried to describe COCOMO2 cost estimation model and has made changes in the power size to improve this model,, where sf-but-PMATJ can be replaced sf, he calculates it by the sum of 4 items TEAM,RESL,FLEX,PRES. Of course, the basis of COCOMO 2 costs estimate model theory is presented in [15,17].

Professor Lotfi Zadeh presented fuzzy theory in Paper [4], which is contrary to the theory of binary logic and it brings out the binary logic from the situation that is completely true and false and gives more flexibility to it .

At [15], the authors have used the fuzzy set for COCOMO model81, Musi1ekp and others in paper [16] have used the fuzzy set for f-COCOMO model.

In paper [6] they have fuzzified COCOMO 2 model Using fuzzy logic. They used EMS,SF,SZ entries for fuzzifying COCOMO2 Where EMS includes 17 multiplicative factors in calculating PM, and SF includes 5 Accumulative factors in calculating b, and SZ is the value of Sloc.

In paper [11] they have used Fuzzy Logic to offer cost estimate suggestion. They have used sugeno type with model input and size and variable effort output for fuzzifying COCOMO. Then to continue the work, they have applied two generalized triangle and bell membership functions, and they have compared Them with the original COCOMO model.

The authors In paper[8] attempted to estimate the cost of object-oriented software with neural and fuzzy. They introduced usp(use case size point), they used of uusp, fta, faa factors To obtain this index.

In [1] First, they tend to describe the three European research project For agent-oriented software cost estimation that the projects are excellent sources of information for obtaining results. Then they proceeded to review the basic concepts, such as sloc,ufp in COCOMO2 Metric Projects Management. in this paper a table of digits and numbers needed for the three projects is Presented that they used 7 items in sloc calculations According to the arguments presented in it . In this paper, two methods are proposed for calculating sloc . The results obtained in the PM, months calculations were compared with actual cost and COCOMO That almost better results have been achieved.

In Article [2], as well as Article [1] They are trying to offer a solution to improve PM also they define three agent-oriented research projects and Effective factors in COCOMO 2. They define a new relationship, to determine the amount of sloc they Have Mentioned it as total sloc .by Multiplying the b arithmetic items average in their Amount, and summation of them, they calculate sloc size to determine the PM. Then they compared The results obtained in this way to the traditional mode, and they achieved better results than the traditional mode. Total Sloc were calculated from equation 1, The event,rule,goal,task, state machines factors were considered To calculate the cost of an agent-oriented .

Total weighted Sloc = AЕ ∗ (#E) +AR∗ (#R) +AG∗ (#G) + Aт ∗ (#T) + As ∗ (#S)                    (1)

Where A£ is average event and AR is average rule and AQ is average goal and A T is average task and Ag is average state machines in sloc for 3 projects .

• III.    Definition

• A. Agent Definition

  In 1990 Mr yaushodham introduced a new concept in programming as agent that its definition was changed in 1993. Therefore, based on the Oxford Dictionary definition, an agent is a personal factor that is qualified to do something In one place with permission of another person.

Many people Have expressed the agent definition,One of the definitions that is provided by sofer is so:

Agent is stable software entity, which is designed to achieve a particular goal.

In computer science,a software agent is a piece of software which acts such as an agency in a relationship with a user, program or other agent.

Russell defines agent such this:Agent is a single computing unit such as software program or a robot, which is visible and it is connected to its environment and it is gained by experiences and adjusts its behavior and the and reacts to the environment and it is an autonomic. The Agents have some goals,which their actions are in order to reach them. Based on the According Russell definition, agents are divided into five floors of the classes according to the degree of intelligence and their features:

• 1    simple reflex agents

• 2    model based reflex agents

• 3    goal- based agents

• 4    utility-based agents

• 5    learning agents

The agent architecture has a decisive role in the specification and behavior of the agent. Types of agent architecture can be in one of the categories below.

• 1  Logical model that is symbolic, and uses the

reasoning mechanism.

• 2    The interaction model that responds based on performing an action.

• 3    A layer model is a combination of the other models.

• 4    BDI(belief, desire, intention) has Mental structure, and is one of the most popular models.

Layered Architecture and BDI are the most famous using models in architecture that consider in Different methodologies. since factors operate in a common environment to reach a goal, they need a common language to understand each other.many companies and Institutions have operated to create agents dialogue Language and standard such as : ACL by FIPA or KQML and WSDL corporation .three tools that Agent-Oriented offers to the users to develop and manage Complexity, are: breaking, Abstraction and organization, by breaking the space of problem,complicated system breaks to agent parts and Communications,by Abstraction, agents seem appropriate for design and construction and the third case represents their efficiency for modeling and management of organizational relationships to reach dependencies and relationships inside the complicated system.

According to the above reasons,and also the other advantages of using multi-agent systems In solving engineering problems,such as :increasing reliability, extensibility, reuse, the possibility of parallel execution, the interaction of parallel systems, possibility of Implementation of Other field`s Scientific theories, Agent-based complicated systems of software engineering,were introduced as the new guidelines in software engineering.

B.Problem Definition as a source of information,we are using three European research projects which have been explained in article [1].these projects are not exactly like industrial projects, because their budget and time can`t change and it`s not expected to sell products of these projects.

Eures com p815: compilation of relationship management processes by using agent software : in this project agents help management applications of Workflows .our share is specified in these projects and agents run by helping of users and via the management of intelligent and dedicated service network`s innovative environments. in these projects,the main subject is the interactions of agents for users and their ability to cooperate existing systems. at the end we implement two kinds of agents: Private management agents,(PMA) to help the management of projects and the private developer agent (PDA) to develop the projects.

Eurescom p907.message: a method for agent software engineering systems: the main results of this project are defined according to the message /uml method. to test this method,we design a helping path. in this implementation,there are three kinds of agents: helping private agent which states users in system and information finder agent which is responsible for searching information sources that is responsible for searching information sources related to the airport and the infoaena agent which covers airport information sources.

PSI3:private service`s interaction by agent software: this is an ACTS project that in this project we implement information of filtering systems as a group. these systems try to create virtual societies for users which every user registers and just receive interesting information. every user in system is exposed via an agent which is aware from user`s current tendencies and new things he has learnt .all of these three projects create an excellent source of information to reach the results. their size is more than simple applications,because the time average of each project is considered from one year and it is more for developer. for more information you can visit this site :http//garsia.fdi.ucm.es.Some data on 3 projects come in the tables1,2,3.

Table 1. statistical data about the implementation of project p815, p907, ps13, paper [2]

Element	P815	P907	ps13
Number of classes	482	172	130
Number of packages	45	31	23
Average methods per class	5.17	4.09	5.3
Number of Event	61	10	10
Number of rule	198	48	39
Number of goal	135	29	------
Number of task	71	9	39
Number of state machines	5	10	8
Sloc logical lines	15843	5393	9862
Sloc physical lines	20009	7007	13102

Table 2. scale factors applied to the projects,paper[2]

Scale factors	P815	P907	Ps13
Procedentness	Nominal	High	high
Development flexibility	High	High	nominal
Architecture/risk resolution	Extra high	Extra high	nominal
Team cohesion	High	Very high	Very high
Process maturity	Low	nominal	Nominal

Table 3. cost factors applied to the projects, paper[2]

Cost drivers	P815	P907	Ps13
Product reliability and complexity	High	Nominal	Very high
reusability	Very high	Very high	Nominal
Platform difficulty	High	Very high	High
Personnel capability	Nominal	Nominal	Nominal
Personnel experience	Low	Nominal	High
Facilities	Nominal	High	High
Required development schedule	Nominal	nominal	Nominal

• C. COCOMO Definition

COCOMO principle comes from implicit cost model. the word “implicit” means complexities and ambiguities of the model can be understood because of the simplicity of the model. this ability permits us to know exactly why the model evaluates it. In 1981 dr bohem, invented this model for the first time,he had big steps in the evolution process of today software.until today many actions have been done in order to correct and improve software evolution techniques and process application programs and many changes have been done. Science engineers have done many proceedings for limited use of this software, finally they have succeeded in parts : (off-the-shelf) become ready to use, packed software(cost),design and management of evolutional process of software, have more advancement,so that today software is reachable as a product for public.

These changes made engineers to correct current model .so, California university as well as software engineering center(use-cse),and organizations which are members of COCOMO 2 project council, decided to present COCOMO 2 model,so they wanted to remove all of its deficiencies and present a non-defective model. today the edited COCOMO (COCOMO2) can be very useful in application software of estimating costs. The evaluation of how much do software projects cost, is done according to their size, human resources,and time.COCOMO2 shows the other parts in different ways:

• 1    source line codes(sloc):one line of codes refers to the least parts that a programmer can produce. however, there are some elements which are not sloc such as: break line character,explanations or compiler instructions.

• 2    Unadjusted function points (ufp):they state the amount of agency in a software project and a set of dedicated project factors. they can be used at the beginning of the project,when the source codes are not reachable yet, to determine the desired size for the system.ufp usually is translated to sloc. the base of main COCOMO  model [10] is rather

development effort(DE).

DE=a*(size)^b                                  (2)

Which the size will be counted in the guidance of thousand delivery sources.a and b constants,depend on the mode of projects` development. And also DE is being counted by every individual per month.

PM =A* sizeЕ∏1г=1 EMi                        (3)

A=2.94(for COCOMO 2,2000)

E=scale factor(table 6)

PM is the period of time that a person has devoted to complete the software process during the month. the main COCOMO limits the correctness because it can not handle ironware and personnel .modern tools and their properties are being used to influence on cost projects. Before, Boehm`s goal was COCOMOs average,[10,14]. He multiplied drive cost by an equal to a new variable to increase the correctness of the main COCOMO: EFA (Try to adjust the factor) that is indicated in table 4.

Table 4. DE for intermediate COCOMO, paper [11]

Development mode	Intermediate Effort Equation
Organic	DE=EAF*3.2∗ (SIZE) .OS    I
Semi-detached	DE=EAF*3.0*(SIZE) .
Embedded	DE=EAF*2.8*(SIZE) .

The expression “EFA” is the multiplication of 15 costs drives [12,13] that is indicated in table 5.

For example: If in a project Rely=low, Cplx=extra high Time=very high,STDR=high, rest parameters=nominal, then, EAF = 0.75*1.08 *1.65 * 1.03*1.06*1.

If the value of all 15 drives is normal the value of EAF equals to 1.Generally drive costs divides into four categories[10,14]

Product: Rely,DATA,CpLX

Platform:TIME,STOR,VIRT,IuRN

Personnel:ACAP,AEXP,PCAP,VEXP,LEXP

Project:MODD,TOOL,CSED

Table 5. Intermediate COCOMO cost drivers with multipliers[11]

n	Cost Driver Symbol	Very low	Low	Nominal	High	Very high	Extra high
1	RELY	0.75	0.88	1	1.15	1.40	_
2	DATA		0.94	1	1.08	1.16
3	CPLX	0.70	0.85	1	1.15	1.30	1.65
4	TIME	_	_	1	1.11	1.30	1.66
5	STOR			1	1.06	1.21	1.56
6	VIRT		0.87	1	1.15	1.30
7	TURN		0.87	1	1.07	1.15
8	ACAP		0.87	1	1.07	1.15
9	AEXP	1.29	1.13	1	0.91	0.82
10	PCAP	1.42	1.17	1	0.86	0.70	_
11	VEXP	1.21	1.10	1	0.90
12	LEXP	1.14	1.07	1	0.95
13	MODP	1.24	1.10	1	0.91	0.82	_
14	TOOL	1.24	1.10	1	0.91	0.83
15	SCED	1.23	1.08	1	1.04	1.10	_

Table 6. Scale Factor Estimation

Name	Very low	Low	Nominal	High	Very high	Extra high
Precedentedness	(0.05)	(0.04)	(0.03)	(0.02)	(0.01)	(0.00)
Flexibility	(0.05)	(0.04)	(0.03)	(0.02)	(0.01)	(0.00)
Significant risks eliminated	(0.05)	(0.04)	(0.03)	(0.02)	(0.01)	(0.00)
Team interaction process	(0.05)	(0.04)	(0.03)	(0.02)	(0.01)	(0.00)
Process maturity	(0.05)	(0.04)	(0.03)	(0.02)	(0.01)	(0.00)

• IV. Mathematical Models

• A.    Fuzzy Element Proposed System

Soft computing are contained, variant types of fuzzy systems,neural networks, genetic algorithms, etc that Be used in applications effort estimation . Fuzzy theory was developed by Zadeh [4], a new intelligent method offered To solve several problems than the old calculations.

We have considered The event, rule, goal, task, state machines features to aspect oriented effort estimate. event, rule, goal, task, state machines are as inputs to proposed system for aspect oriented software effort estimation . Then these features were fuzzy, in order to determine the exact value of sloc. Finally, the software cost is calculated using COCOMO 2.

The mamdani Fuzzy systems to calculate the exact value for event in sloc Which is named as fuzzy event(FE) is shown(Figure 1).

Input and output variables event in sloc is given in the range 0 to 1 after the change of scale. we consider Three linguistic variables are low, average, high, with triangular membership functions for these variable(Figure 2). Fuzzy rules is presented in Figure3, to determine the exact amount of fuzzy event value by experts working. As an example rules for event element : if event sloc is low then fuzzy event sloc is low, if event sloc is average then fuzzy event sloc is average, if event sloc is high then fuzzy event sloc is high.

Fig. 1. fuzzy event in sloc

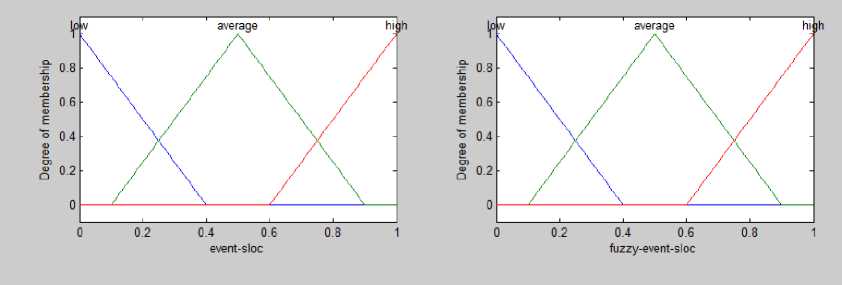
Fig. 2. fuzzy input and output variables for event in sloc

1. If (event-sloe is low) then (fuzzy-event-sloc is average) (1

• 2.    If (event-sloe is average) then (fuzzy-event-sloc is high) (1)

• 3.    If (event-sloe is high) then (fuzzy-event-sloc is high) (1)

Fig. 3. fuzzy rules for fuzzy event in sloc

Fuzzy modeling so done for other parameters the rule, goal, task, state machines as well. Acquiring fuzzy values for each element, we can create equation 4 and as well as convert the equation 1 to relation 5. After fuzzifying lements in sloc, Must be calculated the average value of each element per item. Gaining a new fuzzy total sloc for

each project to wit total pure fuzzy sloc and total weighted fuzzy sloc, are calculated the effort of projects using COCOMO2 method by placement in equation 3.

Total Pure Fuzzy Sloc = FE+ FR+ FG+ FT+ FS (4)

Where FE is fuzzy actual event and FR is fuzzy actual rule and FG is fuzzy actual goal and FT is fuzzy actual task and FS is fuzzy actual state machines in sloc for 3 projects .

Total Weighted Fuzzy Sloc = FAЕ ∗ (#E) + FAR∗ (#R) + FAG ∗ (#G) + FAT ∗ (#T) + FAg ∗ (#S) (5)

Where FA g is fuzzy average event and FAg is fuzzy average rule and FAQ is fuzzy average goal and FA T is fuzzy average task and FAg is fuzzy average state machines in sloc for 3 projects .

In addition to fuzzifying the elements in sloc,number of elements fuzzify To improve the results and we got new relationship 6 from 5. Figure 4,5 is presented membership functions and fuzzy rules for fuzzifying number of element after change scale to range 0 -1.

Fig. 4. fuzzy input and output variables for number of event

Fig. 5. fuzzy rules for fuzzy number of event

Total Weighted Fuzzy Sloc with fuzzy element = FA E ∗ (#FE) + FAR ∗ (#FR) + FAG ∗ (#FG) + FAT∗ (#FT) + FAs ∗ (#FS)                              (6)

In equation 6,FAg is fuzzy average event per fuzzy Item and FAg is fuzzy average rule per fuzzy Item and FA Q is fuzzy average goal per fuzzy Item and FA T is fuzzy average task per fuzzy Item and FAg is fuzzy average state machines per fuzzy Item in sloc for 3 projects, #FE is fuzzy number of events and #FR is fuzzy number of rules and #FG is fuzzy number of goals and #FT is fuzzy number of tasks and #FS is fuzzy number of state machines.

We used geometric mean and Harmonic mean instead of the arithmetic mean for average fuzzy element per fuzzy item,Further research to investigate more deeply. We obtained the equations 9 and 10 Using equations 7and 8, in which Gj,Hj are geometric meen and harmonic meen sloc per element .

geometric meen √х .х2 …….хn(7)

harmonic meen =(8)

⋯

Total geometric Fuzzy Sloc with fuzzy elem = FGg∗ (#FE) + FGR ∗ (#FR) + FGG ∗ (#FG) + FGT ∗ (#FT) + FGs ∗ (#FS)(9)

Total harmonic Fuzzy Sloc with fuzzy element = FHE ∗ (#FE) + FHR ∗ (#FR) + FHG ∗ (#FG) + FHT∗ (#FT) + FHs ∗ (#FS)(10)

• B.    Fuzzy Combinatorial Proposed System of Density

Elements

In the last section we were considered the variables into separate factors. Then we have created for each individual fuzzy rules. But in this part We proposed the following system (figure 6) and created the fuzzy rules after fuzzifying event sloc per number of event(event-density), rule sloc per number of rule(rule-density), goal sloc per number of goal(goal-density), task sloc per number of task(task-density), state machines sloc per number of state machines(satate machines density) features combination of these factors(figure 7).

Input and output variables in sloc per item Were scaled change to 0 - 1. we bring up Three linguistic variables are low, average, high, with triangular membership functions for these variable(Figure 8). Finally, the software cost is calculated using COCOMO 2.

Fig. 6. fuzzy proposed system for elements density in sloc

1. If (event-dens is low) and (rul-dens is low} and (goal-dens is average) and (task-dens is low) and (state-dens is low) then (sloe is average) (1) |2. If (event-dens is average) and (rul-dens is average) and (goal-dens is low) and (task-dens is high) and (state-dens is average) then (sloe is low) (1)

• 3.    If (event-dens is high) and (rul-dens is high) and (task-dens is low) and (state-dens is high) then (sloe is high) (1)

Fig. 7. fuzzy rules for proposed system with for elements density

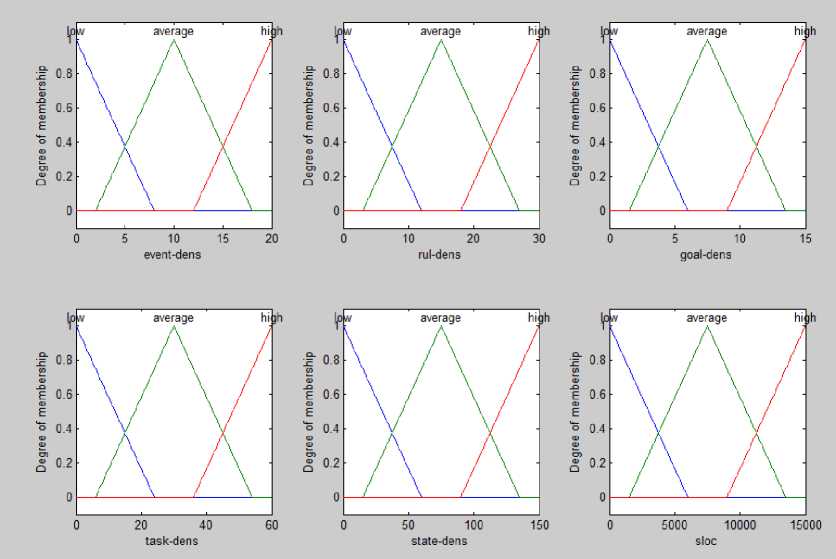
Fig. 8. fuzzy membership function for proposed system with elements density

• V. Experimental Results

We implement our proposed system in MATLAB version 7.12 on Laptop, 1.7 GHZ CPU. Then the exact value of elements are calculated after scaled to range from 0 to 1 Dividing the value of each element, for each project, by the largest amount of that element in projects(table 7).As shown in Figure 11 when the event p815 =1 the Fuzzy event, 0.87 respectively and for p907 when event =0.194 the fuzzy event Obtained 0.545(figure 12).also in PSI3 when event =0.388 the fuzzy event Obtained 0.824(figure 13). To avoid repetition, the following calculation is explains only one element of the project. Considering the figure 14, for p907 when rule =0.433 the fuzzy rule Obtained 0.866. fuzzy goal Was calculated 0.5 in p907(figure 15). For the task element in p907 Was computed when task=0.655, fuzzy task=0.855 (figure 16).Finally, each of state machines for p907 =0.659 Obtained fuzzy state machines =0.854 (figure 17).

Table 7. elements Been scaled to the range 0 to 1.

Element	P815	P907	Ps13
Event	1	0.194	0.388
Rule	1	0.433	0.491
Goal	1	0.069
Task	1	0.655	0.382
State machines	0.135	0.659	1

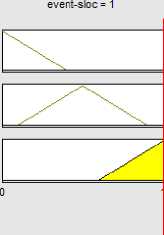
Fig. 11. The exact amount for p815 fuzzy event

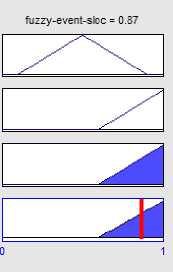
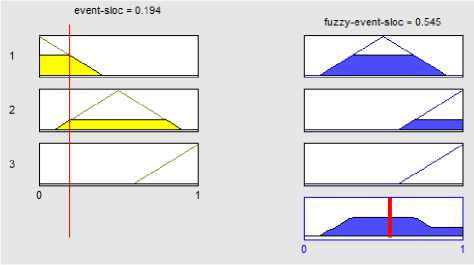
Fig. 12. The exact amount for p907 fuzzy event

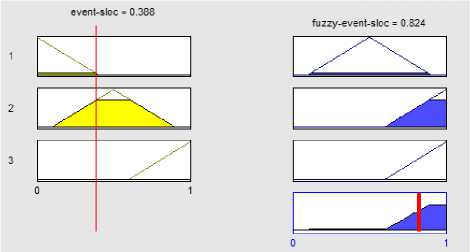
Fig. 13. The exact amount for PSI3 fuzzy event

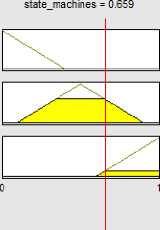
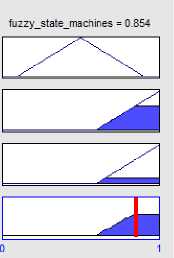
Fig. 17. The exact amount for p907 fuzzy state machines

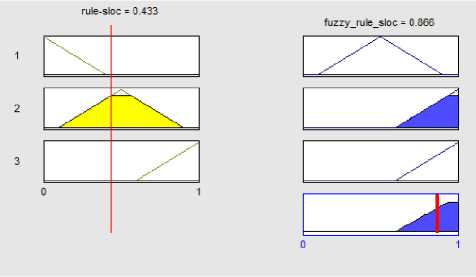
Fig. 14. The exact amount for p907 fuzzy rule

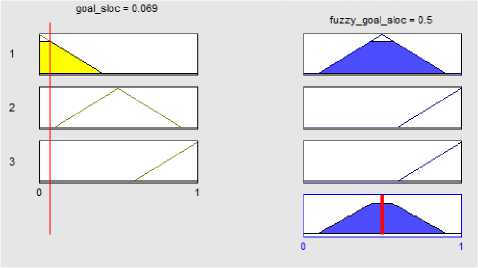
Fig. 15. The exact amount for p907 fuzzy goal

The scaled Fuzzy elements are Obtained in Table 8.The actual amount Fuzzy elements are calculated after scaled Multiplying the value of each fuzzy scale element, for each project, by the largest amount of that element in projects from table 1(show table 9).

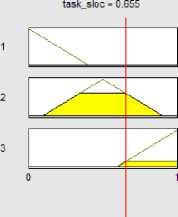
Fig. 16. The exact amount for p907 fuzzy task

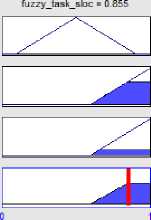
Table 8. results for scaled fuzzy element into sloc.

element	P815	P907	Ps13
Scales Fuzzy Event	0.87	0.545	0.824
Scales fuzzy Rule	0.87	0.866	0.87
Scales fuzzy Goal	0.87	0.5
Scales fuzzy Task	0.87	0.855	0.806
Scales fuzzy State machines	0.513	0.854	0.87

We then calculate the fuzzy average sloc per items with fuzzy actual elements, To apply Equation 4,5,6,9,10 and obtain a new value for the total fuzzy sloc to calculate new value for the cost of software using COCOMO 2. The comparison sloc is given in the table 10 for 3 projects, Column c,d,e,f,g,h were obtained from Equation 1,4,5,6,9,10 respectively.

In proposed system fuzzy combinatorial density elements for project p907 When event-density =8.6 and rule-density=19.2 and goal-density=3.79 and task-density=57.8 and state machines density=69.1 sloc =2450 Obtained(figure 18).

Then we have used usc COCOMO 2 program In order to compute effort [17](figure 19-22). effort was calculated 29.3PM,10.1 months for Project p907 using the traditional method (figure 19) Whereas Obtained 6.6 PM,6.5 months with total weighted sloc from equation 1 respectively(figure 20). But as noted in the figure 21, we find that effort Obtained 7.3 PM,6.7 months the with fuzzy combinatorial proposed system of elements density. The effort Was calculated 44.8 PM,12 months for PSI3 with fuzzy combinatorial proposed system of elements density that result was much better than previous methods(figure 22).

Comparison the effort obtained by usc COCOMO 2 tool Are given in the table 11. Difference between the projected cost to the actual cost is obtained in table 12. According to the data in Table 12, for p907 project Minimum Deviation from the real cost is 0.6 with Total weighted sloc approach and p815 project Minimum Deviation is 0.3 with Harmonic mean for fuzzy sloc per item, Finally PSI3 project Minimum Deviation from the real cost is 24.2 with fuzzy combinatorial proposed system of elements density.

Table 9. results for actual fuzzy element into sloc.

element	P815	P907	Ps13	Average sloc per item
Actual Fuzzy Event	385.41	241.435	365.03	22.32
Actual Fuzzy Rule	1853.1	1844.58	1853.1	31.76
Actual Fuzzy Goal	1375.47	790.5	0	18.72
Actual Fuzzy Task	689.91	678.015	639.15	33.81
Actual Fuzzy State machines	537.624	894.992	911.76	103.66
Total Sloc	4841.514	2393.23	3769.05

In this study, The Magnitude of Relative Error (MRE) will be used, Among the available indicators, in order to compare models and cost estimates. MRE for each observation i can be obtained as:

MMER = - ∑1 MERi n

MER =

| Actual Efforti-Predicted Effort^ | Predicted Efforti

According to the data table 13, the least amount of MMER for all 3 projects using fuzzy combinatorial proposed system of elements density approach and equal amounts of 0.32786, respectively.

Mean Magnitude of Relative Error (MMRE) can be achieved through the summation of MRE over N observations:

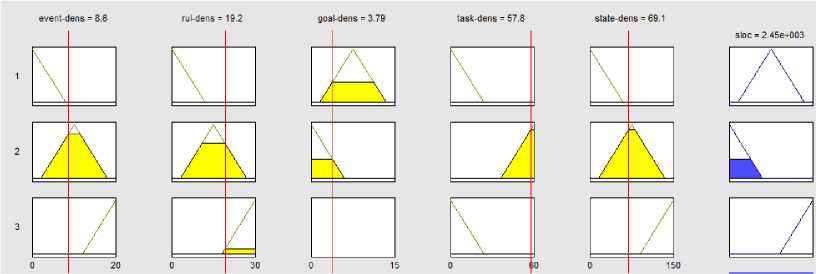
Fig. 18. The exact amount for p907 fuzzy combinatorial proposed system of elements density

Table 10. Comparison the SLoc obtained for projects

P#	traditional(A)	Total sloc agent element(B)	Total weighted sloc (C)	Total pure fuzzy agent sloc(D)	Total weighted fuzzy sloc (E)	Total weighted fuzzy sloc *fuzzy element (F)	Geometric mean For fuzzy sloc per item(G)	Harmonic mean for fuzzy sloc per item(H)	fuzzy combinatorial proposed system of elements density(I)
P907	5393	2330	2236	4449	3632	4071	3990	3908	2450
P815	15843	5089	7666	4841	13098	5916	5802	5687	7500
PS13	9862	2570	2455	3769	3610	3769	3369	3280	12900

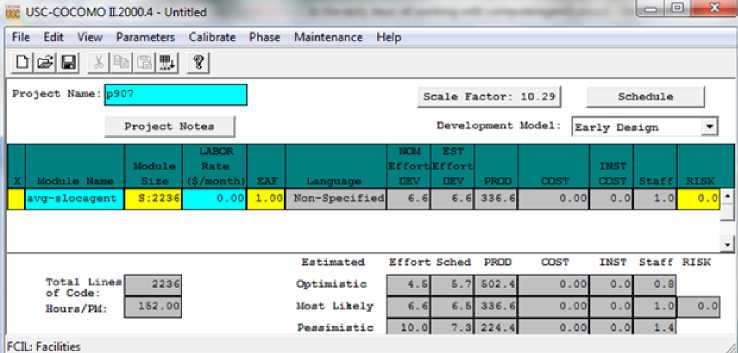
Fig. 20. The effort for p907 with total weighted sloc from equation 1

Table 11. comparison the effort obtained by usc COCOMO 2 tool.

Project	Real cost	Traditional (A)	Total sloc agent element (B)	Total weighted sloc (C)	Total pure fuzzy agent sloc(D)	Total weighted fuzzy sloc (E)	Total weighted fuzzy sloc *fuzzy element (f)	Geometri c mean For fuzzy sloc per item(G)	Harmonic mean for fuzzy sloc per item(H)	Fuzzy combinatorial proposed system of elements density(I)
P907	6PM, 5 months	29.3PM, 10.1months	6.9PM, 6.6 months	6.6 PM, 6.5months	13.3 PM, 8months	10.9PM, 7.5months	12.2 PM, 7.8months	11.9 PM, 7.7months	11.7 PM, 7.7months	7.3 PM, 6.7 months
P815	18PM, 9 months	118.8PM, 16months	16.3PM, 8.7months	25 PM, 9.9months	15.4PM, 8.5 months	44PM, 11.8 months	19.1 PM, 9.1months	18.7 PM, 9.1 months	18.3 PM, 9months	24.5 PM, 9.8 months
PS13	69PM, 18 months	62.8PM, 13.3months	8PM, 7months	7.7 PM, 6.9months	12.1 PM, 8months	11.5 PM, 7.9months	11PM, 7.7months	10.7 PM, 7.7 months	10.4 PM, 7.6 months	44.8 PM, 12months

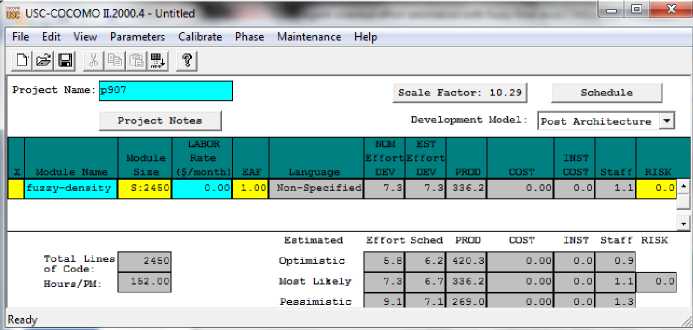
Fig. 21. The effort for p907 with fuzzy combinatorial proposed system of elements density

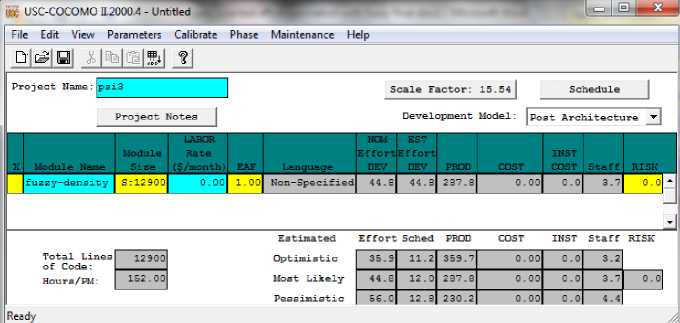
Fig. 22. The effort for PSI3 with fuzzy combinatorial proposed system of elements density

Table 12. comparison the Deviation from the real cost

prj	real	Tradi-tional-A	Total sloc agent element-B	Total weighted sloc (C)	Total pure fuzzy agent sloc(D)	Total weighted fuzzy sloc (E)	Total weighted fuzzy sloc *fuzzy element (f)	Geometric mean For fuzzy sloc per item(G)	Harmonic mean for fuzzy sloc per item(H)	fuzzy combinatorial proposed system of elements density(I)
P907	6	23.3	0.9	0.6	7.3	4.9	6.2	5.9	5.7	1.3
P815	18	100.8	1.7	7	2.6	26	1.1	0.7	0.3	6.5
PS13	69	6.2	61	61.3	56.9	57.5	58	58.3	58.6	24.2
sum		130.3	63.6	68.9	66.8	88.4	65.3	64.9	64.6	32

Table 13. comparison the mmre

Project	Traditional (A)	Total sloc agent element(B)	Total weighted sloc (C)	Total pure fuzzy agent sloc(D)	Total weighted fuzzy sloc (E)	Total weighted fuzzy sloc *fuzzy element (f)	Geometric mean For fuzzy sloc per item(G)	Harmonic mean for fuzzy sloc per item(H)	fuzzy combinatorial proposed system of elements density(I)
P907	23.3	0.130435	0.090909	0.548872	0.449541	0.508197	0.495798	0.487179	0.17808
P815	100.8	0.104294	0.28	0.168831	0.590909	0.057592	0.037433	0.016393	0.265306
PS13	6.2	7.625	7.961039	4.702479	5	5.272727	5.448598	5.634615	0.540179
MMRE	43.43	2.61991	2.777316	1.806728	2.013483	1.946172	1.993943	2.046063	0.32786

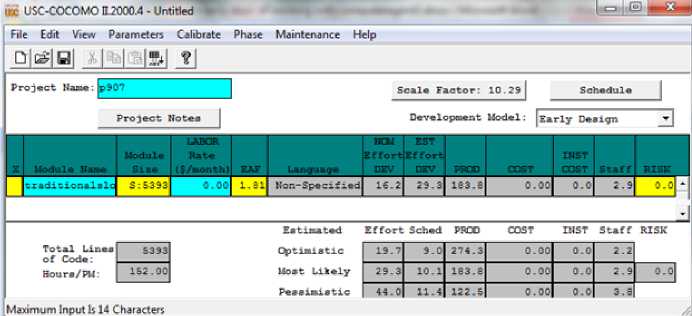
Fig. 19. The effort for p907 with traditional sloc

VI. Conclusion

Our purpose in this research is prediction the exact amount of agent oriented software effort and creating an algorithm for this purpose, as yet,many mentioned algorithms are offered in literature review,and we suggested some methods also.The event, rule, goal, task, state machines features were considered In order to The agent-oriented software cost estimation .To use this feature Was caused agent oriented software size estimates more accurate than the real value.

the new values size obtained By applying different methods based on these features namely Total sloc agent element,Total weighted sloc,Total pure fuzzy agent sloc,Total weighted fuzzy sloc,Total weighted fuzzy sloc *fuzzy element,Geometric mean For fuzzy sloc per item,Harmonic mean for fuzzy sloc per item,fuzzy combinatorial proposed system of elements

density.Finally, was calculated COCOMO2 amount of effort using each method.

between these methods in” fuzzy combinatorial proposed system of elements density” offered algorithm, the amount of Mean Magnitude of Relative Error (MMRE) indicator is lesser than the existing proposed algorithms and the performed calculations in experimental results in table 13,prove this claim .in order to perform future works, the proposed algorithm for agent oriented software’s can be developed with Raising The data relating to projects, and also Neural methods can be used in order to determine the exact amount of effort in industrial environments. Probably to be achieved better results By changing the number of linguistic variables, the type of membership function, the number of fuzzy rules as well as changes in the factors considered for the agent oriented software.