Fuzzy-Based System for Determining the Severity Level of Knee Osteoarthritis

Numerous techniques have been applied over the past decades to solve medical problems: expert systems, artificial neural networks, linear programming and database systems are a few samples of the approaches used, however, fuzzy logic seems to have an edge over these techniques because it provides a simple way to arrive at a definite conclusion based on vague, ambiguous, imprecise, noisy, or missing input information and allows intermediate values to be defined    between conventional evaluations like true/false, yes/no, high/low, hence a more human-like way of thinking in the programming of computers [1].

The task of medical diagnosis, unlike other diagnostic processes is made more complex because a lot of vagueness, linguistic uncertainty, hesitation, measurement imprecision, natural diversity are all prominently present in medical diagnosis. With improvement in science and technology, intelligent computing has been used assisting in enhancing qualitative services, thereby reducing the mortality rate and also alleviating the economic burden placed on the society through lost working time as well as social and medical costs due to one ailment or the other of which osteoarthritis is not an exception. Fuzzy logic (a paradigm of artificial intelligence), provides a mathematical tool for dealing with the uncertainty and imprecision typical of human reasoning has been used in assisting the medical personal in making decision [2]. Fuzzy can also be described as a tool of artificial intelligence based on the observation that people make decisions based on imprecise and non-numerical information [3]. Using fuzzy logic in medical diagnosis is a promising technique that can easily capture the required medical knowledge and come up with sound diagnosis decisions. Practically, an expert physician tends usually to specify his experience in rather fuzzy terms, which is more natural to him than trying to cast his knowledge in rigid rules having abrupt premises [4].

Osteoarthritis (OA) is a type of arthritis that is caused by the breakdown and eventual loss of cartilage for one or more joints. It is the most common form of arthritis and the major cause of activity limitation and physical disability in older people [5]. It is characterized clinically by pain, enlargement and deformity of the joints and limitation of motion. Among the most commonly affected sites in osteoarthritis, the knee is the major source of reported disability and loss of function [6]. Some other words used to describe osteoarthritis, including osteoarthrosis’, ‘arthrosis’ and ‘degenerative joint disease’. Osteoarthritis of the knee is a very common form of osteoarthritis. Other joints which are often affected include joints in the hands, the spine, the hip joint and the big toe joint. Osteoarthritis (OA) of the knee is a major public health issue causing chronic disability and reduction in quality of life, there is no cure nor an objective or accurate method for measurement of the structural severity in general clinical practice [7], hence the need to develop a system that will determine the level of severity of knee osteoarthritis so as to reduce the pain and physical disability associated with significant social and economical burden. This paper reports the development of a fuzzy system that allow to determine the level of severity of knee osteoarthritis, given some input conditions, the system was implemented and simulated using MATLAB 7.6.0 Fuzzy Logic Toolbox .

The remaining part of this paper is arranged as follows: a brief review of related works, presentation of a fuzzy logic controller, the fuzzy logic controller design, model simulation, discussion of results and conclusion.

• II.    Related Works

The first major commercial application of fuzzy logic was in the area of cement kiln control, an operation which requires that an operator monitor four internal states of the kiln, control four sets of operations, and dynamically manage 40 or 50 "rules of thumb" about their interrelationships, all with the goal of controlling a highly complex set of chemical interactions. One such rule is "If the oxygen percentage is rather high and the free-lime and kiln-drive torque rate is normal, decrease the flow of gas and slightly reduce the fuel rate" [1].

In [8], a fuzzy logic temperature controller for preterm Neonate incubator was designed. The goal was to attain thermoneutrality and also the efficient

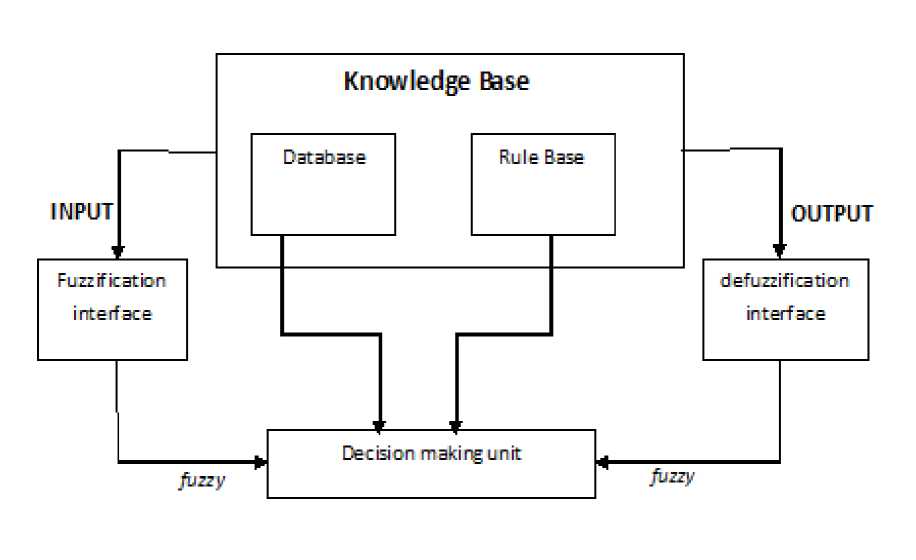
Fig. 1: Major Components of a fuzzy-based system Adapted from [13]

stabilization of the incubator temperature at a desired value

and

thereby      prevention

of

hypothermia/hyperthermia related diseases/conditions and death. Fuzzy Logic modeling has been used in many medical applications [9]. The medical decisionmaking process is often complicated which makes it an attractive area for fuzzy systems modeling. It has been proposed that health and disease as concepts are best understood as fuzzy sets and that illness and wellness are really fuzzy states of health. [10] describes a fuzzy-logic-based expert system for the classification of sleep disorders where fuzzy sets are used to ‘qualify’ diagnostic criteria in terms of frequency, intensity, quantity and graduated yes–no variables. Warren et al [11] presented a decision support system for automating the application of clinical practice guidelines based on fuzzy methods. Other fuzzy diagnostic systems have been reported, for example, in rheumatoid arthritis [9]. This research work offers an alternative and often complementary approach to conventional approaches to modeling system.

• III.    Fuzzy Logic Controller

Generally, a Fuzzy logic Controller comprises of four principal components: a fuzzification interface, a knowledge base, decision-making logic, and a defuzzification interface [12]. The figure below shows the basic configuration of a fuzzy logic controller.

• A.    The Fuzzification interface

The fuzzification converts the input data namely KneePain, Stiffness, Swelling and Crepitus into suitable linguistic variables. A scale mapping is performed using triangular membership function, which transfers the range of input variables into corresponding universe of discourse.

• B.    Knowledge Base

The knowledge base consists of database and rule base. The database provides necessary definitions that are used to define linguistic control rules with syntax, such as: IF THEN . The ‘IF’ part is called the ‘antecedent’ and the ‘THEN’ part is called the ‘consequent’. In this work, the antecedents are “k neePain ’, ‘ stiffness ’, ‘ crepitus ’ and ‘ age ’ and the consequent is the ‘s everitylevel ’.

• C.    Decision Making Logic

The decision making logic infers a system of rules through the fuzzy operator ‘AND’ and generates a single truth value which determines the outcome of the rules (inferred fuzzy control action).

• D.    Defuzzification

Defuzzification is a process in which membership functions are sampled to find the grade of membership; this grade is then used in the fuzzy logic equation(s) and an outcome region is defined, from which the output is deduced. Over the years, several defuzzification techniques have been suggested. The most frequently used ones are the centroid or centre of area, centre of sums, and mean of maxima .

• IV.    The Fuzzy Logic Controller Design

During fuzzification, the fuzzy input variable, KneePain ranging from 1 to 10 is converted into four linguistic grades namely Grade1 , Grade2 , Grade3 and Grade4 . Similarly, the input variable Age ranging from 45 to 75 is converted into five linguistic variables namely:   VeryYoung , Young , MiddleAge , Old and

VeryOld . The other two fuzzy input variables; Stiffness and Crepitus and the output variable SeverityLevel ranging from 1 to 10 are converted into five linguistic levels namely: VeryMild , Mild , Moderate , Severe and VerySevere . The triangular membership function is used to perform the scale mapping.

• A.    The Controller Inputs

The function of the controller is to determine the severity level of knee osteoarthritis which can be determined by knee pain (the major determinant) and any other three of the knee osteoarthritis symptoms.

The researcher made use of knee pain, which is graded into four grades:

Grade1 when the patient can ignore the pain without taking drugs or pain reliever

Grade2 when the patient can ignore the pain by taking drugs once in a while

Grade3 when the patient can only ignore the pain by consistently taking of drugs

Grade4 when the patient cannot ignore pain, even while consistently taking drugs.

The inputs S tiffness, and C repitus use the linguistic variables VeryMild, Mild, Moderate, Severe and VerySevere MF using the triangular MF formulation, while the last input variable Age uses the linguistic variables VeryYoung, Young, MiddleAge, Old and VeryOld.

• B.    The Controller Output

In this research work, MISO fuzzy system is applied, hence the only output variable used in this work is SeverityLevel which determine the level of severity of knee osteoarthritis giving the input variables.

• C.    The controller’s Linguistic Rules (Fuzzy IF-

• THEN Rules)

Based on the choice of inputs and output as discussed in section 3.3.1 and 3.3.2, the following fuzzy IF-THEN rules are extracted from the set of rules that represents an expert knowledge about how best to determine the severity level of knee osteoarthritis

IF (k neepain is grade4 ) and (s tiffness is verysevere ) and (c repitus is severe ) and ( age is veryYoung ) THEN ( severitylevel is verysevere ).

IF (k neepain is grade3 ) and (s tiffness is severe ) and (c repitus is severe ) and (a ge is young ) THEN (s everitylevel is severe ).

IF (k neepain is grade2 ) and (s tiffness is mild ) and (c repitus is verymild ) and (a ge is middleage ) THEN (s everitylevel is mild ).

IF ( kneepain is grade3 ) and ( stiffness is verysevere ) and (c repitus is moderate ) and (a ge is veryYoung ) THEN (s everitylevel is severe ).

IF (k neepain is grade4 ) and (s tiffness is moderate ) and (c repitus is moderate ) and (a ge is veryYoung ) THEN (s everitylevel is severe ).

• D.    Decision Making Logic

The decision making logic infers a system of rules through the fuzzy operator ‘AND’ and generates a single truth value which determines the outcome of the rules (inferred fuzzy control action).

• E.    Defuzzification

Defuzzification is a process in which membership functions are sampled to find the grade of membership; this grade is then used in the fuzzy logic equation(s) and an outcome region is defined, from which the output is deduced. Over the years, several defuzzification techniques have been suggested. The most frequently used ones are the centroid or centre of area, centre of sums, and mean of maxima .

• F.    Centre of Area Defuzzification method

In centre of area (COA) defuzzification, the crisp value u is taken to be the geometrical centre of the output fuzzy value µ_OUT ( u ), where µ_OUT( u ) is formed by taking the union of the contributions of all the rules whose degree of membership function is greater than zero. The centroid methods are based on finding the balance point of the whole geometric figure. The defuzzified output is defined as

• V.    FLC Design

During fuzzification, the fuzzy input variable, KneePain ranging from 1 to 10 is converted into four linguistic grades namely Grade1 , Grade2 , Grade3 and Grade4 .

Similarly, the input variable Age ranging from 45 to 75 is converted into five linguistic variables namely: VeryYoung , Young , MiddleAge , Old and VeryOld .

N

u = ^-----

^E H out u i )

The other two fuzzy input variables; Stiffness and Crepitus and the output variable SeverityLevel ranging from 1 to 10 are converted into five linguistic levels namely: VeryMild , Mild , Moderate , Severe and VerySevere . The triangular membership function is used to perform the scale mapping

where the summation is carried out over discrete values of the universe of discourse, µi, sampled at N points.

In the centre of sum defuzzification method, the overlapping areas of multiple rules are taken into account more than once. The defuzzification output is defined as

u =

Nn

E uE Hk u)

i = 1       k = 1

The behavior of the control surfaces is defined by the rules that join the fuzzy variables together. In this work, 500 rules were framed with the assistance of a Rheumatologist. All the rules are presented in the form of a rule base matrix, where the antecedents are the KneePain , Stiffness , Swelling and Crepitus and the consequent of the rules is SeverityLevel .

The non-fuzzy crisp output from the FLC is obtained by carrying out defuzzification using the centre of gravity method.

Nn

^^ ^^ Hk (Ui) i=1 k=1

E.H(x,) х-u \hVv)

where N represents the number of sample points and n represents the number of rules.

where x Is a running point in a discrete universe

This is the another method to defuzzify the output by taking the crisp value with the highest degree of membership in µ OUT , When there is more than one element with the maximum value in the universe of discourse, then the mean value of the maximum is taken or randomly select one of them. Suppose there is M such maxima in a discrete universe of discourse. The crisp output can be obtained as:

h(x)

is its membership value in the membership

function and ‘u’ is the crisp output value.

M

u = y um M

Where u m is the mth element in the universe of

discourse in which the membership function H   ( u )

is at its maximum value, and M is the total number of such elements. The height of a fuzzy set A, i.e. h (A) is the largest membership grade obtained by any element in that set.

The defuzzification yields a crisp, non-fuzzy control action from an inferred fuzzy control action. In this research work, the centroid method is used as the defuzzification strategy.

A total of 500 rules were generated for this research represented by 4 linguistically designed input with the ‘kneepain’ having four (4) membership function and the remaining three input variables: ‘stiffness’, ‘crepitus’ and ‘age’ are all having five membership function each. This number results from the membership function say (x) raise to the number of input-variable, since the variable ‘kneepain’ has four membership functions and the other three have five MFs each, then the total number of rules = 53 x 4 = 500. Rules generation in fuzzy system follows human reasoning pattern which make it more flexible in composition. It is just like a dialogue taking into cognizance the pros and cons on a circumstance. In the rule viewer provided by the Fuzzy inference System (FIS) in fig. 2, sliding the red line changes the input values and, and generate a new output response, also, the inputs can be set explicitly using the edit field.

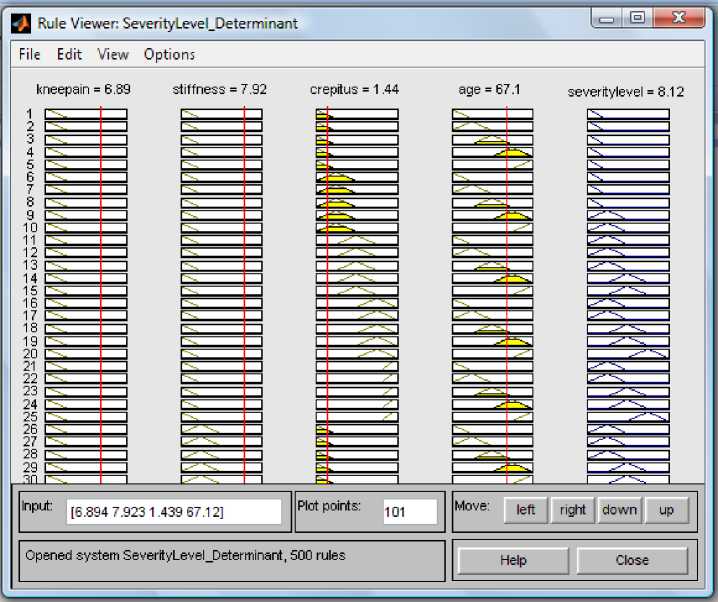
Fig. 2: Sample Rule Viewer

The simulation of this work was carried out with Matlab 7.6.0 for windows. Designation of values for membership function determination is an important phase in fuzzy system designs. With the membership function, each variable is allocated a level of association with other variables and their membership functions. The membership function for the input variable “kneepain” is as shown in figure 3:

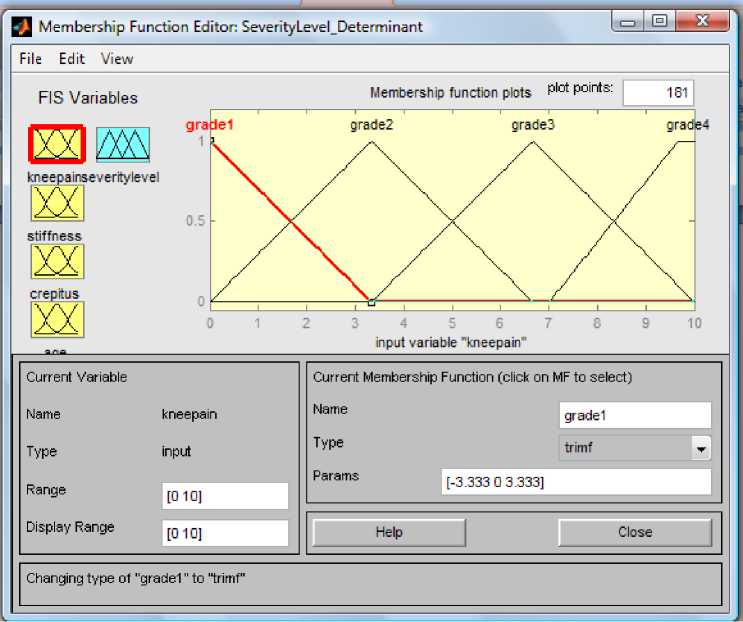
Fig. 3:Membership function for the input variable “kneepain”

The input variable “kneepain” was plotted against another variable “stiffness” to observe the relationship between both parameters “kneepain” and “stiffness”. The relationship is as shown in figure 4.

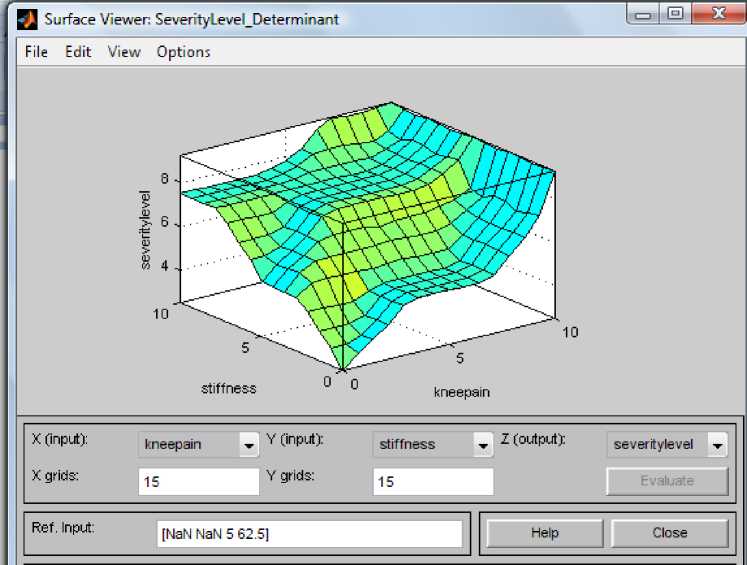
Fig. 4: Surface viewer for stiffness versus kneepain

Another factor considered in the course of the research is the effect of natural phenomenon like age on the level of severity of knee osteoarthritis.

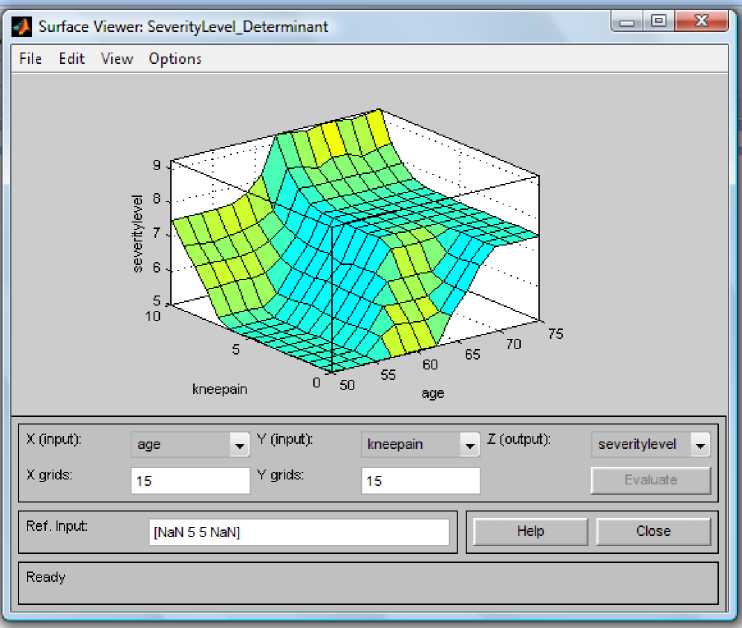
Fig. 5: Effect of natural phenomenon

• VII.    Discussion of Result

When the parameter “kneepain” was plotted against the variable “stiffness”, it was clearly observed that the higher the kneepain and s tiffness , the higher the severity level (s everitylevel ) of the system and vice versa. The model takes into cognizance factors like crepitus and age. Peak requirement for high severity level is when both the kneepain and the stiffness are ‘verysevere’ . The importance of fuzzy inference is the ability to combine the effect of multiple factors and come up with a holistic view of the prevalent scenario. In the figure 4, the system combines adequately factors like ‘kneepain’, ‘crepitus’ and ‘age’ amongst other and present the fuzzified results in the level of severity. The presented simulated results are in three-dimensions. This is because presently it is difficult to represent higher dimensions without distorting the figure in Matlab tools. This has limited the number of variables to be considered to two against the fixed variable (output). It has not in any way however hindered the functionality of the system because each factor represented is depicted as an integral part of the whole system whose variables has been fuzzified.

Similarly, when “age” was plotted against “kneepain”, the peak of this appeared only when kneepain is in grade4 and age is above 60 years as represented in figure 5 and this accounts for why knee osteoarthritis is common among older adults.

Other combinations of the input variables can be generated in similar manner. The evaluation of the severity level shows a system that can effectively handle the dynamic symptoms for determining severity level in patient with knee osteoarthritis and it also assist the physician in taking appropriate measure and educate the patient on how to go about managing the different severity level to avoid further injury to the knee. The computer based systems were used to analyze using different assumed values and the output shows that the software is robust enough for the determination of severity level in knee osteoarthritis.

• VIII.    Conclusion

This paper has presented a fuzzy inference system designed to determine the severity level based on identified factors (input variables). Knee osteoarthritis has no cure, but if diagnosed on time, it can be managed. With fuzzy based system, severity level can be determined and the ailment properly managed based on the usage of linguistic variables and the membership function developed for them. As opposed to expert systems, fuzzy system employs linguistic variables which facilitate human description using their natural language. With this development, knee osteoarthritis symptoms only need to be inputted in natural language term and not precise values. The results are entrusting and promising based on the flexibility and case of adaptability.

• [1]    Zadeh, L. A. Making computers think like people,” IEEE. Spectrum, 8/1984, pp. 26-32.

• [2]    R. Radha , S. P. Rajagopalan “Fuzzy logic approach for diagnosis of Diabetics”. Information Technology Journal 2007, 6(1): 96-102

• [3]    Oguzhan Yilmaz, Gunseli Gorur and Turkay, Dereli.; Computer Aided Selection of Cutting Parameters by using Fuzzy Logic: B. Reusch (Ed.): Fuzzy Days 2001; LNCS 2206; pp.854- 870, 2001

• [4]    Buchanan, B. and Shortliffe, E. (Eds.) (1984). “Rule-Based Expert Systems”: The MYCIN Experiments of the Stanford Heuristic Programming Project. Addison-Wesley, Reading, MA.

• [5]  Dunlop D., L. M. Manheim, E. H. Yelin, J. Song

and R. W. Chang. “ The cost of arthritis” in

Arthritis and Rheumatism, 2003, pp. 101-113

• [6]  Urwin, M., Symmons, D. P. M., Allison, T.,

  Brammah, T., Busby, H., Roxby, M., Simmons A. and Williams G. “Estimating the burden of musculoskeletal disorders in the community: the comparative prevalence of symptoms at different anatomical sites and the relation to social deprivation” in Annals of Rheumatic Diseases, 1998, pp.649-655.

• [7]    Oka, H. Muraki,S., Akune, T., Mabuchi, A., T. Suzuki, H. Yoshida, S. Yamamoto, K. Nakamura, N Yoshimura, H, Kawaguchi : “ Fully automatic quantification of knee osteoarthritis severity on plain radiographs ” Osteoarthritis and Cartilage, 2008, 16(11): 1300-1306

• [8]    Bajeh, O. A. and Emuoyibofarhe O. J (2008) “A fuzzy logic temperature controller for preterm neonate incubator” Proceedings of the first International Conference on Mobile Computing Wireless Communication, E-health, M-health and Telemedicine (MWEMTem) 2008, vol. 1, pp. 158170

• [9]    Leitich, H., Adlassnig, K. P. and Kolarz, G., Development and Evaluation of Fuzzy Criteria for the Diagnosis of Rheumatoid Arthritis, Methods of Information in Medicine 35:334– 342, 1996.

• [10]    Ohayon, M., Improving decision making processes with the fuzzy logic approach in the epidemiology of sleep disorders. J. Psychosom. Res. 1999; 47, 297–311

• [11]    Warren, J. G. Beliakov and B. Van der Zwaag, Proc. 33rd Hawaii International Conference on System Sciences, IEEE, 2000, pp. 1578.

• [12]    Chuen Chien Lee, “Fuzzy Logic Control Systems: Fuzzy Logic Controller – Part I” IEEE

  Transactions On Systems, Man And Cybernetics. 1990, Vol. 20. No. 2 pp. 404 – 418