Fuzzy inference system optimization by evolutionary approach for mobile robot navigation

Published Online February 2018 in MECS

The obstacle avoidance and the choice of shortest trajectory are the essential components to achieve successfully autonomous navigation. Several trajectory tracking and path following algorithms have been proposed to steer the mobile robot along a path to a desired goal [1], [2], [3], [4], [5]. There are some famous classical navigation methods that must be cited: the potential field method, vector field histogram and the method of deformable virtual zone, the first one introduced by [6], whose idea is to imagine the virtual forces acting on the robot. This method assumes that the robot is driven by virtual forces that attract it towards the goal, or reject it away from the obstacles. The actual path is determined by the resultant of these virtual forces, the second method is introduced in [7] which corresponds to local occupancy grid, constructed from the sensors of the robot; this method was improved in [8].The method of deformable virtual zone [9] is also very effective, most of it is suitable for any form of obstacles. The method fuzzy limit-cycles for the problem of obstacle avoidance of mobile robots in unknown environment, this method proposes a hybrid approach based on limit-cycles method and fuzzy logic controller. The purpose of hybridization consists on the improvement of basic limit-cycle method in order to obtain safe and flexible navigation [10].

Many researches turned their attention to the obstacle avoidance algorithms inspired from artificial intelligence tools and relatively suitable for real-time and embedded applications can be cited: Neural Network: This approach is applied in [11] to solve the problem of obstacle avoidance during manipulation tasks performed by redundant manipulators. The developed solution is based on a double neural network that uses Q-learning reinforcement technique. This paper focuses on calculating inverse kinematics and obstacle avoidance for complex unknown environments, with multiple obstacles in the working field. The author in [12] proposed a new local collision avoidance algorithm between multiple agents for real-time simulations. This approach extends the notion of velocity obstacles from robotics and formulates the conditions for collision free navigation and robot path planning. The authors in [13] described how to apply a genetic algorithm in finding a globally sub-optimal path for the robot group working under certain tasks. The problem of path planning for a robot group is formalized as a multiple travelling salesman problem (MTSP), that employed either total-path-shortest or longest-path-shortest as the evaluating criterion. The author in [14] studied the problem of multi-robot target searching in unknown environments. For target searching, robots need an efficient method with respect to their limitations and characteristics of the workspace. The author proposed a distributed algorithm based on Particle Swarm Optimization (PSO) for target searching which satisfies the before-mentioned constraints. This extension of PSO is named A-RPSO (Adaptive Robotic PSO).

These methods have been carried out in off-line manner in completely known environments. However, these methods are not suitable for navigation in complex and dynamically changing environments where unknown obstacles may be located on a priori planned path. Thus, the sensor based local path planning, so called obstacle avoidance, carried out in on-line manner is required in the navigation of mobile robots.

In order to achieve autonomous navigation of a mobile robot and to avoid such a criticism, our work proposes fuzzy control architecture based on two tools: Fuzzy logic and evolutionary approach. A number of criteria of fuzzy logic justified his choice. Among them is the principle of regulation and control by fuzzy logic approach to human approach in the sense that the variables are not dealt with logical variables but linguistic variables, close to human languages, these variables are treated using rules that refer to a certain knowledge of the behavior of the controlled system. Also fuzzy logical lows to take into account the uncertainties from the sensor data and consequently the environment in which the mobile robot embedded.

The use of fuzzy logic founds different application in the area of control system design, where human expert knowledge, rather than precise mathematical modeling. Of a process or plant is used to model/implement the required controller. Uncertainly and ambiguity are evident in may engineering problems [10]. Fuzzy logic control (FLC) therefore provides a formal method of translating subjective and imprecise human knowledge into control strategies, thus facilitating better system performance through the exploitation and application of that knowledge.

However, the efficiency of the fuzzy controller depends essentially on its inference system (sets of fuzzy rules). For this reason, we used evolutionary approach inspired by the ant colony optimization ACO and genetic algorithm operator to obtain the best membership functions for a fuzzy control system. These methods are largely used in optimization problem resolution.

The main objective of the proposed architecture is to reduce the robot orientation change in obstacle avoidance behavior. Without affecting the efficiency and the safety of the avoidance.

The remainder of the paper is organized as follows: Section II gives the principle of reasoning and fuzzy control. Section III validates the fuzzy controller with results. Section IV and section V presents the optimization evolutionary algorithm system for autonomous navigation inference, section VI proposes contribution with results. Finally, we conclude and give some perspectives in section VII.

• II.    Autonomous Navigation by Fuzzy Logic

This section describes the obstacle avoidance and attraction to the target in unstructured environment. We proposed and developed a reactive navigation control system using fuzzy logic. The robot reacts according to the changes in its environment. The fuzzy controller developed is a classical version, used for multi-input, multi-output processes and uses Mamdani approach for outputs generation [15] [16].

The fuzzy system determines the two wheels speed so the robot avoids obstacle and reaches the goal. The reflex action of the robot is derived from the analysis of data according to the three sides of the robot (dG, dF, d and dD: the obstacles distances) and polar coordinates of the end point in the coordinate system of the robot (the orientation of the target denoted γ) and the distance to the Target denoted d.

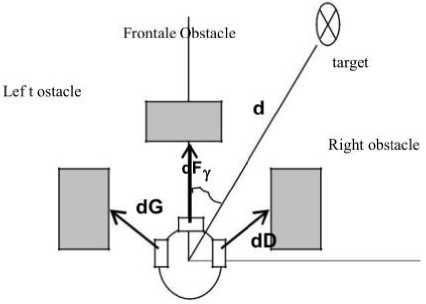
Fig.1. Mobile robot localization

In the following, we describe different stages of the fuzzy control for navigation (Fuzzification, fuzzy inference and Defyzzification).

• A.    Fuzzification

During the development of a fuzzy control system, membership functions are defined in three points:

• (1)    The general shape of the membership functions is based on the particular problem knowledge.

• (2)    Some parameters belonging to the membership function remain fixed in order to ensure the correct system behavior in boundary conditions.

• (3)    An adjustment method is performed for the remaining parameters.

Each of the above input variables and output variables are converted into its corresponding linguistic fuzzy set.

For our fuzzy control for navigation, we use triangular membership functions.

Inputs fuzzification

Figure 3 presents the two membership functions of the distances: dG, dF, d and dD. The choice of these membership functions have been fixed after several tests.

Membership degree

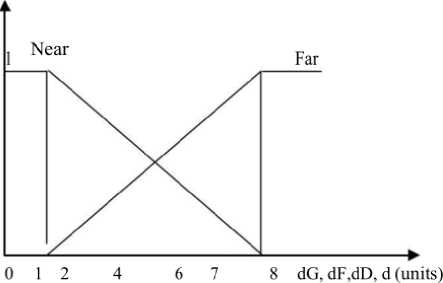
Fig.2. Representation fuzzy sets in the distance

Outputs fuzzyfication

The outputs of our fuzzy system are the orientation change ( Δ θ ) and speed change ( Δ V) of robot.

The orientation change is represented by five fuzzy sets: TGG (theta great left), TGP (theta little left), TZ (theta zero), TDP (right small theta), TDG(theta right large).

Membership degree

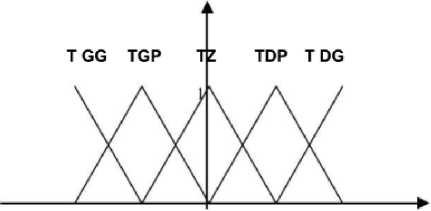
-30     -15      0     15    30 A0(degree)

Fig.3. Representation of the fuzzy sets of the output Δ θ

• B.    Inference Rules

This step presents the inference rules elaboration to determine the robot behavior according to its intrinsic parameters. It will be seen later that the number of potential rules of reaction increases directly with the number of labels of the variables.

At end we have 80 fuzzy rules. The following table summarizes the rules for the detection of a frontal obstacle case:

Table 1. Inference for situation: Avoid near Front

Ей 9	dG	dF	dD	d	7		AS	Av
IF	L	P	L	L	GG	then	TGG	ZAC
	L	P	L	L	GP		TGP	ZAC
	L	P	L	L	Z		TGP	ZAC
	L	P	L	L	DP		TDP	ZAC
	L	P	L	L	DG		IDG	ZAC
	L	P	L	P	GG		TOG	DEC
	L	P	L	P	GP		TGP	DEC
	L	P	L	P	Z		TGP	DEC
	L	P	L	P	DP		TDP	DEC
	L	P	L	P	DG		TDG	DEC

• III.    Simulation and Results

To confirm the relevance of the proposed control navigation, it is proposed to simulate a mobile robot navigation to reach a target in presence of obstacles for different environments configurations.

Figures 4 and 5 show navigation examples in different environments containing several static obstacles with different geometrical shapes.

Fig.4. Environment 1

Fig.5. Environment 2

To reach the target, the robot must avoid the obstacles and choose the best path.

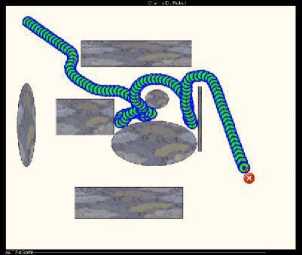
Fig.6. Environment 3

In some environment configurations, the robot cannot reach target, or he chooses a non-optimal path (fig. 6). We note, however, that all behaviors are not applicable in the same way depending on the environment situation.

• A. Comparison of fuzzy logic and vector field histogram approach

To assess the viability of fuzzy logic approach, it is appropriate at this stage to compare the performance of Fuzzy logic method with other standard method. The vector field histogram approach has been used in mobile robotic. The performance of the vector field histogram is presented in this section and they are compared with fuzzy logic method performances presented in the previous section. The same environments are applied to the vector field histogram approach.

• • The Vector Field Histogram

The Vector Field Histogram (VFH) method [17] is a real-time obstacle avoidance method that permits the detection of unknown obstacles and avoids collisions while simultaneously steering the mo-bile robot towards the target. The VFH method uses a two-dimensional Cartesian histogram grid as a world model. This world model is updated continuously with range data sampled by on-board range sensors. The VFH method subsequently employs a two-stage data-reduction process in order to compute the desired control commands for the vehicle. In the first stage, a constant size subset of the 2D histogram grid considered around the robot ’ s momentary location is reduced to a one dimensional polar histogram. Each sector in the polar histogram contains a value representing the polar obstacle density in that direction. In the second stage, the algorithm selects the most suitable sector from among all polar histogram sectors with a low polar obstacle density, and the steering of the robot is aligned with that direction.

The three main steps of implementation of the VFH method are summarized:

•

•

•

Builds a 2D Cartesian histogram grid of obstacle representation,

From the previous 2D histogram grid, considers an active window around the robot, and filters that 2D active grid onto a 1D polar histogram, Calculates the steering angle and the velocity controls from the 1D polar Histogram, as a result of an optimization procedure.

In order to test more affiance of the approach (Fuzzy logic), we compare in figure the robots trajectories obtained with fuzzy logic and the vector field histogram for different simulation cases of obstacle avoidance.

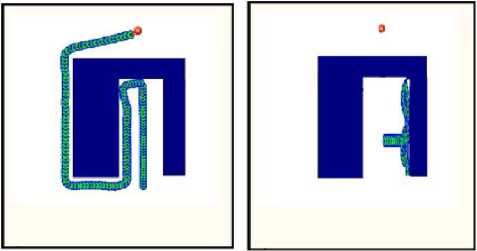
The figure 7 shows that the robot able to reach the target with the two methods (Fig. 7 (a) and (b)) essentially when the environment without obstacles. Otherwise in the figure 8 (a) the robot reach target and it choose the optimal path but in case (b), the robot is in a blocking situation.

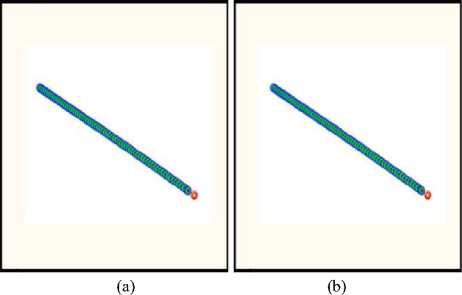
Fig.7. (a) Fuzzy logic environment 1, (b) vector field histogram environment 1

(c)                                (d)

Fig.8. (c) Fuzzy logic environment 2, (d) vector field histogram environment 2

In practice, fuzzy logic is a good empirical approach, it gives satisfactory results in different environment and compared with other existing methods of navigation such as the vector field histogram, but unfortunately the results are not always optimal. In order to increase the efficiency of fuzzy logic, we will add a learning module for our fuzzy controller. For our case, this module is based on an evolutionary approach.

• IV.    Learning of Fuzzy Inference System by Evolutionary Approach

The conventional navigation methods like the potential field method, vector field histogram and the method of deformable virtual zone are classic algorithms that will produce same result by following the same computational steps. But it however suffers from some disadvantages like high time complexity in high dimensions and problems of getting trapped in local minima.

The main motivation behind the hybridization of fuzzy evolutionary is to exploit the complementary character of the both methods, to take benefit from advantages of fuzzy logic and evolutionary approach for resolution of complex problem navigation in dynamic environment (cognitive behavior of inference fuzzy system and optimization and learning skills of evolutionary approach).

The proposed evolutionary algorithm can be used for structural synthesis of fuzzy controllers, this is to generate an optimal set of linguistic rules and their membership functions, or it can be used to find optimal membership functions for a set of specified linguistic rules.

For our case study, we opted for the first approach to learning the optimization fuzzy rules necessary for navigation of the mobile robot. (Reach the target in the best conditions, no collision and optimum trajectory).

In a very general way, the evolutionary algorithm is considered a metaheuristic method, where each solution is represented by an agent moving in the search space. Agents mark the best solutions and take into account of previous markings to optimize their research.

Although this method has shown its effectiveness in solving many difficult problems, it is, however, difficult to adapt. This is mainly due to the considerable number of parameters to define [13]:

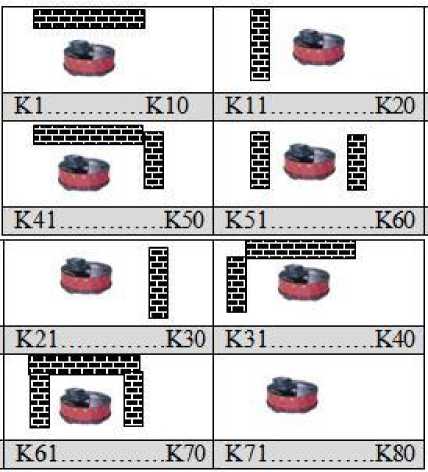
Fig.9. Solution representations.

•

•

•

Determination of the population size, Initial population

Solutions evaluation,

B. Adaptation Function

All learning methods require estimation about the performance, also known as reward, it is important to choose wisely this function to achieve the learning behavior of obstacle avoidance; reward used is divide din:

•

•

•

Minimize the rotations of the robot;

Minimize the number of collision.

Minimize the path length.

The interest of such learning is to enable the robot to find itself the optimal strategy. The following figure shows the principle of learning strategy by evolutionary algorithm.

The evolutionary computational approach is inspired by the ant algorithm and genetic operator. We create a population of ant (each ant present an inference table for robot navigation). This population of ant struggle to survive and reproduce for the next generation. The reproduction mechanism in this population is based on genetic operator (crossover, mutation).

It is very difficult to model analytically the behavior of the robot in navigation. In this context, the evaluation criteria that we have adopted are a system of adaptation. It is given a degree of adaptation rule for each table created by the robot's behavior. Each solution generated by the evolutionary algorithm implemented in the fuzzy controller. We start the navigation process, and then the system will support adaptation assessment of robot behavior according to this solution.

To evaluate the performance of a mobile robot navigation, we must define the essential criteria that make a navigation is better than another. These criteria are:

The number of collisions made by the robot with obstacles during navigation;

The length of the path;

The time required to reach the target (time);

The number of turns performed by the mobile robot around obstacles;

• V. Determining Evolutionary Algorithm Parameters

• A. Initial solution generation

The solutions starting in general are random; each solution presents in the form of a vector whose number of elements is the number of inference rules (80 rules in our case) and the vector represents a conclusion K i representing the variation of the speed and direction of the robot. For better control of learning parameters, we organized rules block (8 blocks) and each block consists of 10 rules that corresponds to a situation among the 8 possible situations which can be encountered by the robot.

Each evaluation criterion is aggregated in a fitness function.

Collision number

^{f N} collis

= ^ N

^г( f N Collis <0,1 ] ) collis ^_

( N _ collis = 0)

The path length function

Dist

( f Dist Dist

^G[ 0,1 ] )

The turn number fN_tour

,  ¹     f^or ^ [ 0,1 ]

N tour ^_

0 N tour >  N tour max

The time needed to reach the target (Time)

This criterion is strongly linked to the length of the test track.

In this context we have not presented this criterion by evaluation function since is indirectly presented by the function f Dist

Adaptation function

Adaptation function overall behavior of the robot is the combination of the three functions described above:

f traj

f N cols ( af DSst + bf N tour ) *100 a + b

Where:

a and b are weighting coefficients.

In this function, we gave more importance to the function fN_collis because our first objective is the avoidance of obstacles.

• •    cases with bad behavior

To escape deadlock situations in which a robot can fall during the navigation, we set maximum time navigation and a maximum number of collisions. We stopped a bad behavior if:

• •    It exceeds the maximum time navigation

• •    It exceeds the maximum number of collision

• C.    Determining the agents population

The greatest difficulty in this algorithm is the generation and fixing the size of the parameters of the solution. The choice of agent ’ s number who belongs to the population is empirical.

From the initial solution, we generate vectors of agents where each of them represents a vector of outputs inference rules. For this operation, we applied a permutation stochastic process between the elements of initial vector solution (figure 10).

a , b e [0,1]

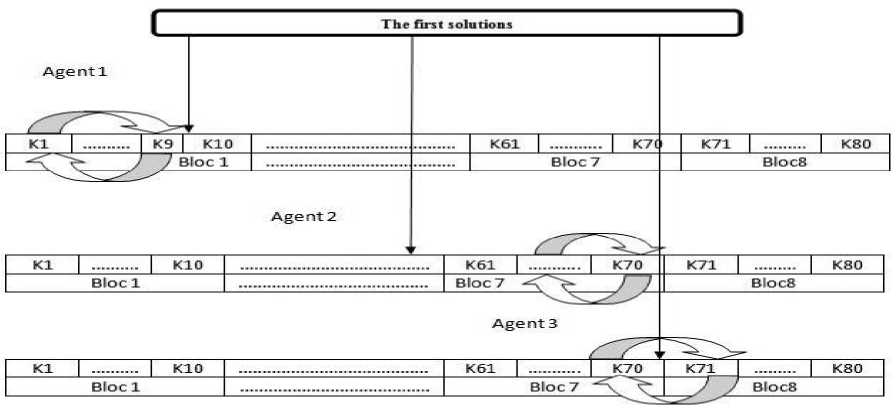
Fig.10. Generating of agent population

Each agent is evaluated against its cost (function f traj ).

After, we classify agents in ascending order according to their costs.

• D.    Structure of the algorithm

The population of agents includes agents Ae "elitist" and A- Ae "not elitist."Elitists ensure the convergence of the algorithm, while non-elitist explore the search space to maintain the diversity of solutions and prevent the diversity of solutions [15].

In Table of the solutions, we rank as the cost of each agent, the order of this ranking is decreasing.

^ Moving blindly choice

Each agent listed, we use the following approach:

• 1.    Randomly choose two conclusions of the solution (agent) selected.

• 2.    Mutation between the blocks of the 2 agents if the problem constraints are checked.

• 3.    Assess the obtained solution.

• 4.    If the agent is not elitist, replace with the new solution.

• 5.    Reorder the list of agents.

• 6.    Update the path costs.

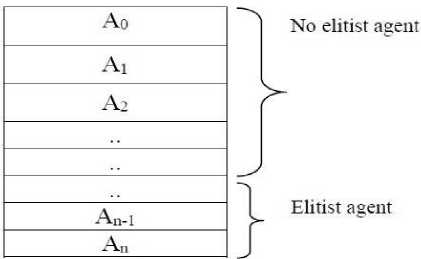
Fig.11. Population structure after ranking

V Displacement not blind choice

For each agent in the list, we follow this approach taking into account the cost of trajectories and the stress of the problem:

Randomly choose a solution (agent) selected.

Change the block assigned to the agent by which the block to the best service and solutions in relation to any of the list.

Evaluate the resulting solution.

Replace the solution if the agent is not elitist.

The following figure shows the approach to the optimization of a fuzzy inference system for mobile robot navigation.

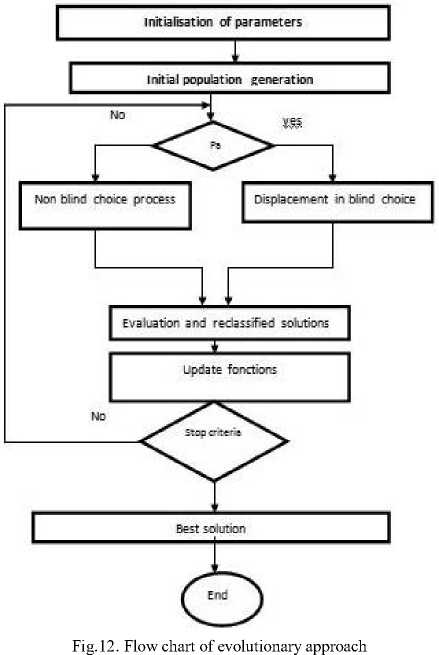
• VI.    Simulation Results after Learning

After we have shown that fuzzy logic an approach that is not fully guaranteed in section 3, we now present the simulation results of navigation by fuzzy system after learning.

To confirm the relevance of the proposed approach, it is proposed to simulate a mobile robot navigation to reach a target in presence of obstacles for different robot configurations and different environments.

Each Simulation is made twice. In the first case (before learning), we used only the fuzzy logic method for obstacle avoidance (Fig.13(ai) and Fig.15(ai)). In the second case (after learning), the proposed approach is implemented on the robot (fuzzy logic method combined with evolutionary approach) (Fig.13(b i ) and Fig.15(b i ). In the cases, the robot reaches the target while avoiding obstacles (before or after learning). However, we can see clearly the impact and the relevance of the learning approach in terms of optimal trajectories, safe navigation and a minimum time.

Pa,: random number generating

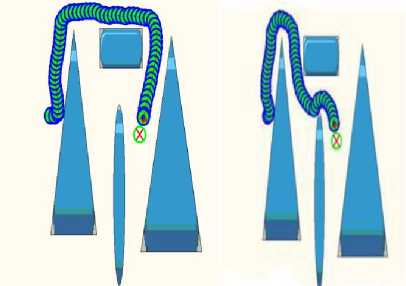
(a ₁ ) Before Learning

(b1) After Learning

Fig.13. Example 1

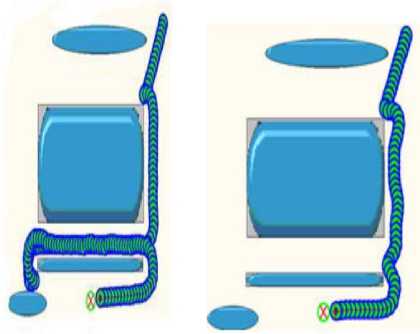
(a ₂ ) Before Learning          (b₂) After Learning

Fig.14. Example 2

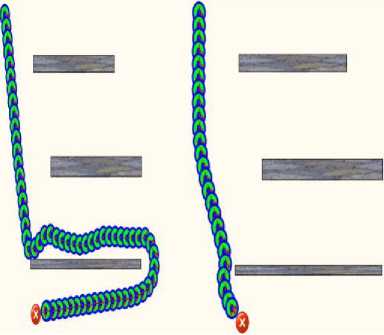
(a 3 ) Before Learning           (b₃) After Learning

Fig.15. Example 3

• VII.    Conclusion

In this work, fuzzy logic controller has been adopted to determine the mobile robot ’ s velocities to the control objectives. An evolutionary algorithm has been also implemented to improve the FLC by optimizing its inputs factors for better efficiency and effectiveness.

The provided simulation results show that the proposed approach acts successfully and enable the robot to track the moving target easily with good performances in term of convergence time and accuracy. The use of evolutionary algorithm to tune the inputs parameters of the FLC makes the robot ’ s trajectory and the controllers ’ outputs much smoother and reduces considerably the convergence time and the tracking errors.

Further works may be directed to extend the result in an environment containing dynamic obstacles and optimize this approach by making it more intelligent and also to make experiments on real robots.