Fuzzy ontology-based approach for the requirements query imprecision assessment in data warehouse design process near negative fuzzy operator

Published Online February 2018 in MECS DOI: 10.5815/ijitcs.2018.02.03

The majority of existing tools for the data warehouse (DW) development “Ref. [4]” focuses on the data storage structure. The focus is on modeling and integration of data from heterogeneous sources, rather than on the decision-making expert needs. Due to the growing DW complexity, constant attention must be paid to assessing their quality throughout their design and development. The DW quality depends on the quality of all requirements, conceptual, logical and physical models used for the DW design.

A good requirements model quality can lead to a good DW quality “Ref. [5]”. Various authors have proposed measures to ensure the quality of conceptual, logical and physical models for DW. However, there is no significant work in the literature to ensure the quality of the decision needs model. In data warehouse designing model, consideration must be given not only to data sources but also to needs analysis. Thus, when the source data or needs analysis changes, a change in the warehouse model may be necessary “Ref. [6]”.

However, the majority of the studies carried out on this first phase show that the request structure is not familiar to those who are not computer scientists “Ref. [7]” and who represent the majority of decision makers in intelligent economic systems. For the flexible evaluation of business intelligence system or the representation of vague, incomplete and uncertain knowledge, fuzzy ontologies are used as an effective solution to these problems “Ref. [8,9]”. Thus, the main contribution of this article is to propose a fuzzy ontology-based rigorous solution to evaluate the flexible decision requests that represent the requirements expression.

This study will showing the convergence of studies to ontology-based conceptualization and indicating that most solutions have ignored the imprecision consideration. Even the few existing studies “Ref. [10, 11, 12, 13]” in the literature dealing imprecision in decision systems have focused studies on the data imprecision and not in queries representing the decision maker’s requirements. Also, the few works that treated the queries imprecision in Databases (DBs) “Ref. [14, 15]” differ from the imprecision treatment in decisional structure, for example, by absence of the OLAP operator in DBs which can present imprecision. Therefore, we focus our study on the fuzzy operator first before considering in the future the fuzzy OLAP operator.

The remainder of this article is organized as follows: The section 2 presents the motivation example. The section 3 presents the work background. Section 4 presents a state of art on the imprecision in requirements expression and on the imprecision assessment of fuzzy operator in database query. We present then an ontologybased DW design. Section 5 presents our proposed approach and presents the application of our approach in a use case study (transportation risk).The section 6 concludes the paper and cite some perspectives.

• II.    Motivation Example

In the road accidents risk study (Given the catastrophic damage caused by road accidents in Algeria1, particularly the large number of deaths each year “an average of 13 deaths per day” and trying to classify the main factors of this scourge), we find difficulties to classify the transport actors (Unacceptable Bus, negligible line, unwanted conductor, etc.) Since this classification is based on historical data (data warehouse) of some parameters set previously by the expert. This problem kind find in our proposal the solution to lift the vagueness and specify the desired classes.

Our proposed solution can be applied either to design a new DW or to update an existent one, in the case where the warehouse does not respond to the fuzzy requirements. For simplification reasons, we assume that we are in the second case. We will briefly present starting with presenting the main classes of our example, namely: Company, Bus, Driver or Conductor, Line, weather and then we present the ontological modeling of a fuzzy query. The company represents enterprise passenger transport (Fig. 1).

In this section, we focus on describing possible updates to a warehouse data model when a decision requirements is assessed differently.

To illustrate this change in the evaluation of the decision requirements and the impacts they have on the DW design evolution, we propose an existing DW on the road transport risks.

Example: The decision maker requirement want to know, in a specific period of time, the company buses and drivers "at risk" (Unacceptable, Unsafe, etc.), for our example the period is the semester. The imprecise decisional requirements are: unsafe bus, unwanted conductor, unacceptable line, etc.

Why using the fuzzy ontology? In order to classify, for example each bus according to its accidents consequences over this period by risk type defined in the ontology and clarify its membership in this class degree. Accidents instances occur in the Company data warehouse and will power the dataset defined in the ontology. This classification allows to take the suitable decision for each actor (Bus, Driver, Line,..).

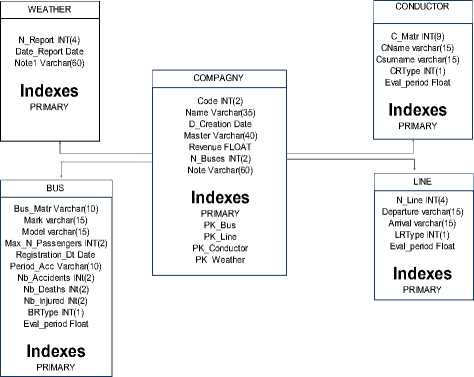
Fig.1. Classes of existent DW

• III.    Background

In this section we first define the decisional requirement to highlight the imprecision in such requirements, then we define the imprecision before presenting our proposed fuzzy ontology solution and finally we present the domain of our motivation example which is the road transport risk.

• A.    Decisional Requirements

In this paper we focus on the imprecision study in the requirements expression, and especially in the querybased requirement.

Requirement: according to “Ref. [15]”, a requirement is a description of a property or properties of the system that must be satisfied. Often, the requirements can be classified into the following categories “Ref. [16]”: (Table 1.)

The decisional requirement can be generally functional but also nonfunctional and rarely QoS requirements.

Example: The unwanted Bus for the last semester/year.

• B.    Imprecision

Imprecision in an OLAP query can be located in clauses that can include inaccurate parts: predicate attribute value, connector, operator, and aggregation. The following table summarizes the possible cases. (Table 2.2)

Table 1. REM features and approaches “Ref. [15]”

Functional Requirements
User-driven	•    Information requirements are gathered from different business users and then integrated and made consistent to have unified schemata. •    Bottom-up technique. •    Active involvement of the users. •    Dependent on knowledge of business users
Data-driven	•    It begins with collection and analysis of operational data sources in order to have an idea of available data. •    Low participation of the users and their requirements. •    Bottom-up technique •    Resulting Schemata is stable as it is based on quality of the transactional data which does not changes often like user requirements.
Goal-driven	•    Revolves around the business strategies and objectives formulated by the top-management •    Involves top-management only. •    Top-down approach •    Tales care of progressive goal refinement from the top-management people.
Non-Functional Requirements
Scenario-Based	Various scenarios are provided to different users, stakeholders, top-level management people and others based on real life situations. Their feedbacks are collected and examined so that the specified expectations and constraints can be converted into requirements for addition into the checklists. Some “soft-scenarios” (based on dummy situations or assumptions) are also generated. “Soft scenarios” represent those scenarios that do not have any straightforward definitions but help in what-if analysis for gathering alternate solutions to conflicting requirements.
QoS Requirements
Usage Models	•    The frequency of usage of each and every module is clearly understood. •    User groups are identified. •    Criticality of available services and their availability is regularly checked. •    Requirements are gathered based on the user groups, frequency of usage and usage decisions.
Role Based Models	•    Users and their roles are clearly specified and identified. •    Permissions are granted based on the roles of various users. •    Hierarchies of roles are also identified. •    Each session is recorded and tracked.
Access Control & authorization	•    Each user is provided with a unique ID & password. •    Access rights are also assigned based on roles. •    Provisions are made in case of loss of identity.

• C.    Fuzzy Ontology

The Fuzzy ontology is defined as an ontology, has, in addition to the basic components (ie, concepts, relationships, axioms and instances), new components according to the fuzzy logic, fuzzy concepts and fuzzy relations. These ensure the representation of a fuzzy universe of discourse parties. A fuzzy ontology consists of six components: (i) the specific concepts, (ii) fuzzy concepts, (iii) precise relationship, (iv) fuzzy relations, (v) axioms and (vi) instances “Ref. [17]”. In our case, in addition to three specific components, we will be interested in fuzzy concepts and axioms relating to these concepts.

Table 2. Imprecision in decisional requirements queries

Fuzzy Part	Example			Explication
Attribute	Select * from Bus where BRType = (is) Acceptable			The imprecision arises in columns or fuzzy attributes (for the case of fuzzy DBs or unclear data sources when designing fuzzy DWs or when OLAP analysis. (This case is interesting for the study of requirements imprecision in the non-fuzzy DW)
Predicate Value	Select Threshold 0.2 LName, Age , Expertise From Conductor Where ~Age IS ‘Middleaged’ AND #Expertise IS ‘AI’			In this case the value of the predicate is unclear. It is a subjective value whose translation depends on the decision maker must also define the trapezoidal function (in general).
Connector	Find risky bus with four-year startup and if possible ABS braking system. Other connectors "failing" "especially since"			It enables the combination of multiple predicates.
Operator	Select     *     from Conductor where Age NEAR 60 Other   operators    : LARGE  POSITIVE; LARGE NEGATIVE; FAR; NEAR   POSITIVE; NEAR NEGATIVE			It is defined by a trapezoidal function and a function defining the relationship between the operands.
Aggregation	Select name, FAVG (Eval) From Conductor Group By age Having FAVG (Eval) > 0.8			Instead of using the AVG function is used an aggregate function FAVG (fuzzy Average) in the clause "Having"
Clauses Order by Group by OLAP Operator	Select a,b,c From A,B WHERE    A.a=B.b GROUPE BY (c)			One may have imprecise in terms of Order by Group by or used with a fuzzy attribute. As may have a fuzzy operator (OLAP operator with a fuzzy attribute) "Drilldown .." used with the Group by clause
UML Classes		Conductor IdConductor Name Doubler With 0.3 DEGREE Fuzzy Age		One may have buses that have no doubler driver, only 30% of buses have doublers. The imprecision is shown with a degree of ability = 0.3 One may have the case of inaccurate attribute (fuzzy)

The ontology taxonomy is composed of three categories: (i) Conceptual Ontologies (CO) represent object categories and properties that exist in a given domain whereas (ii) Linguistic Ontologies (LO) represent the terms used in a given domain eventually in different natural languages. (iii) Non Canonical Conceptual Ontologies (NCCO) include not only primitive concepts but also defined concepts “Ref. [37]”

• D.    Risk & Transportation sector risk

Transportation sector risk: Our illustrative example treat the transportation sector risk especially accident which is the first danger experienced “Ref. [18]” in the transportation and the most dangerous. The several actors of the accident are: The conductor, the bus and the line. There are other actors such as weather which we will not discuss in this paper. These criteria are included in standards as a guide only to limit the decision criteria. Accident indicators are the basis of road safety programs. Accident data are collected for many years as a starting point for improving road safety. The meanings of dangerous situations are: Unacceptable: Must be eliminated ; Unwanted: The risk is acceptable only when the reduction of the latter is impossible; in this case the agreement of the operator or network regulators is imperative; Acceptable: The risk is acceptable with appropriate supervision and agreement of the operator or the regulator; Negligible: Acceptable unconditionally. So, let's apply this matrix in our case of road transport, proposed system. These rules were validated with experts in traffic engineering. So, we will have for example (Table 3.):

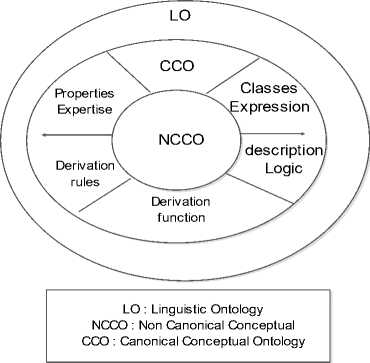
Fig.2. Onion Model. “Ref. [37]

T able 3. Some validate rules of our example

IF	THEN
If (Frequency of dangerous situation is Frequent) and (Severity of the consequences of a dangerous situation is Marginal)	Risk Type is Unacceptable
If (Frequency of dangerous situation is Occasional) and (Severity of the consequences of a dangerous situation is Critical)	Risk Type is Unwanted
If (Frequency of dangerous situation is Rare) and (Severity of the consequences of a dangerous situation is Insignificant)	Risk Type is Negligible

For simplicity representation example, we assume that the bus risk type depends only on the parameters D (Death), I (Injured) set by the expert.

Through this background, we see that this work represent the imprecision study in the decisional requirements only present in the requirement query predicate and especially in the operator part. This study proposes a fuzzy ontology-based solution that will apply to the example dealing with the road transport risk. This work represents a part of open problems in this research2.

• IV.    Related Works

To treat the requirements expression imprecision for the data warehouse design/update, we will present the result of our previous bibliographical study on the requirements analysis, before presenting imprecision in DW and sweeping to ontologies-based data warehouses design solutions.

• A.    Decisional Requirements Analysis & Imprecision treatment

After a previous comparative study “Ref. [19]” of different approaches, it was found that the majority of existing work on decision-making requirements have not considering the requirements expression imprecision. A lot of works look for semantics of the data or use semantics queries without revealing the imprecision at the queries level “Ref. [20, 21, 22]”.

For the few studies which have highlighted this imprecision, we can conclude:

Authors in “Ref. [23]” note the fact that the information requirements expressed by the user might be imprecise and show that a set of ontologies applications needed to generate data that will be stored in the designed data warehouse. These ontologies resemble database diagrams, but they are more flexible in the sense that they provide definitions, inaccurate and implied for the generated data which mean adding annotation data resources for obtaining Semantic DW, the authors in “Ref. [24]” show that requirements for data analyses are often unclear and uncertain, mainly because of incomplete decision processes are flexibly structured and poorly shared across large organizations, but also because of a difficult communication between users and analysts. They also differentiate between the managerial and strategic requirements, the authors in “Ref. [25]” say that ontological knowledge may enrich a multidimensional model in aspects that have not been taken into account during requirement analysis or data-source alignment. So, we can conclude that works “Ref. [23,24,25]” have highlighted the imprecise requirements but they don’t dealt rigorously with vagueness requirements expression, they presented the ontologies as remedies for incomplete, uncertain and unclear data. These works share the fact that they have not proposed approaches or solutions to achieve their observations. Some works as in “Ref. [26]”, the authors have projected the study of both imprecision aspect in queries and uncertainty in the model but we haven’t found a continuity to the study. Although the authors of “Ref. [27, 28, 29]” had used queries for requirements collection, but they did not take into consideration the fuzzy queries.

To the best of our knowledge, there has not been a data warehouse design study based on fuzzy ontology and taking into account the imprecision at the requirements analysis phase and where the requirements are expressed in query form.

• B.    Imprecision Assessment of fuzzy operator in Database query

The authors in “Ref. [30]” introduce two fuzzy operators - NEAR and NOT NEAR, explaining their working and the algorithms to implement them.

The focus of this solution is to find a way to enhance the current database management systems, and enabling them to handle precise as well as imprecise data. The approach taken here for this purpose is to embed fuzziness in SQL language without changing its underlying structure.

This operator deals with the data type NUMBER and DATE. The purpose of this operator is to fetch the nearest possible values to a specific number/date without any need to define the range.

Opl NEAR Op 2              (1)

Here, the Op1 refers to an attribute, whereas Op2 is a fixed value, both of the same data type.

Example:

SELECT id, name, age, history FROM casualties

WHERE cause=’heart attack' AND age NOT NEAR 55;

The NEAR algorithm for the NUMBER data type works as follows:

• •    The margins to the op₂, i.e. ml and m 2 , are added dynamically on both sides, considering the value it contains. This is performed with the help of the formulae, Where:

ml = a - b(2)

m 2 = a + b(3)

a = op 2(4)

b = op 2-1(5)

To keep this margin big is important for a certain reason discussed later.

• •    The NEAR operator is supposed to obtain the values NEAR to the op 2 ,  thus the target

membership degree (md) is initially set to 0.8.

• •    Values till md are calculated on both the sides with respect to the margins added to op₂, with the help of the formulae where:

m _ left = (md * diff 1) + m1(6)

m _ right = (md * diff 2) - m2(7)

diff 1 = op 2 - m1(8)

diff 2 = m2 - op 2(9)

md = membership degree (0.8 initially), ml , m2 = op2 margins

• •    The algorithm compares the op l (column) values row by row, till the end of the table, to the elements of the set that NEAR defined, i.e. values from m_left to m_right, adding matching tuples to the result set.

• •    It is possible that the result set is empty since no values within the range exist in opl. The algorithm checks for empty result set, and in that case, decreases the target md by 0.2 and jumps to step 3. This is the reason big margins to the op 2 are added.

• •    In case there are no values in opl that are between ml and m2 (and thus the result set is empty), the algorithm fetches the two nearest values (tuples) to op₂, one on each side, as the result. (f ig . 3. )

We will adapt this algorithm to our study by focusing on the NEAR NEGATIVE part because taking the value Op 2 , all the upper part of this value (and less than Op 2 of the following class) is obviously a part of the desired class and also we propose the necessary change to our case for the belonging function.

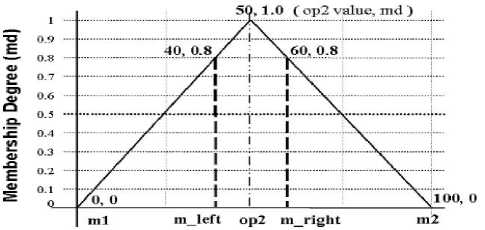
Fig.3. Initial margin target of NEAR “Ref. [24]” (Number Case)

• C.    Ontology-based data warehouse design

Before starting this part, we note that the majority of DW vagueness studies, focuses on data inaccuracies and offer structural solutions. Most of the discovered problems for integrating fuzzy concepts in data warehouse systems are solved by integrating them into a Meta table’s structure “Ref. [32, 33, 34]”, but recent research tends to offer ontologies-based solutions as we will present in the following:

• •    Literature Review: Recent works are interested in ontology-based data warehouse in analytical or operational phase “Ref. [36]” but few studies are interested in this type of structure in the design phase. Several studies (as we will see before) used

to express the decision- making requirements in natural language or in SQL language as goals or objectives to help data warehouse design or to optimize an existing one.

Authors in “Ref. [35]” have proposed a new approach for designing ontology-based data warehouse from a set of Ontology-based databases (OBDBs). Additionally to the nature of sources participating in the construction of their data warehouse, a second important component is the user’s requirements. They’ve proposed to extend the use of ontologies, on the same way as for data sources, to clarify (eliminate ambiguity) and unify users requirements. However, this proposal had allow the designer to express his requirements in natural language and in goals form without SQL reformulation, the reuse of this model is not systematic. Authors in “Ref. [5]” have proposed a method for analyzing decisional requirements, as a process and models that support the discovery, specification, negotiation and validation requirements. This approach aimed to guide analysts and designers throughout the Decisional Business Intelligence process. Traditionally, i* models lack any modularity, suffering from scalability and readability issues, regardless its widespread adoption. In their work “Ref. [37]”, they have presented a proposal for applying modules, specially designed for DWs. They have defined their proposal, and provided some guidelines how to correctly apply it. This solution applies only requirements analysis based-goals but doesn’t apply to based-models nor based-queries models.

Many studies on the ontology-based data warehouse design “Ref. [35, 36, 3, 23]” have used goals-based approaches, but there are fewer studies queries-based or uses case-based models “Ref. [26]”. In their paper “Ref. [38]”, the authors have extended the OWL2 standard to manage fuzzy data; the proposal “Ref. [38] extends the ontology management framework Protégé with capabilities to manage fuzzy data. Several applications of fuzzy ontologies are used for recognition of fuzzy events in summarization and fuzzy decision support “Ref. [39]”.

Before presenting our proposal, we will describe the GLMP ontology (using the expert’s knowledge and including his/her experience) that, in our case, allow us to evaluate the imprecision in the predicate value of the query representing the decider requirement.

• •    Ontological solution - GLMP (Granular Linguistic Model of a Perception) Ontology:

Authors in “Ref. [2,3]” proposed a method about using ontologies to create a computational representation of the expert’s knowledge including his/her experience on both the context of the analyzed phenomenon and his/her personal use of language in that specific context. They called GLMP the proposed ontology model. They inspired their solution from the father of Fuzzy Logic, Lotfi Zadeh work “Ref. [40]”, who has proposed a new direction in his research line, namely extending Fuzzy Logic towards Computing with Words and Perceptions (CWP). The Granular Linguistic Model of a Phenomenon (GLMP) is based on CWP using ontologies as a tool for modeling the meaning of perceptions about complex phenomena.

The GLMP (Granular Linguistic Model of a Phenomenon) Ontology consists of a network of PMs (Perception Mapping). Each PM receives a set of input CPs (Computational Perception) and transmits upwards a CP. We say that each output CP is explained by the PM using a set of input CPs. In the network, each CP covers specific aspects of the phenomenon with certain degree of granularity.

A CP is the computational model of a unit of information acquired by the designer about the phenomenon to be modeled. In general, CPs correspond with specific parts of the phenomenon at certain degrees of granularity. A CP is a couple (A; W) where: A = (a₁; a 2 ;…….;a n ) is a vector of linguistic expressions (words or sentences in Natural Language) that represents the whole linguistic domain of the CP.

Example: ai=” temperature is high”. W = (w 1 ; w 2 ; …..; w_n) is a vector of validity degrees wϵ [0; 1] assigned to each a_i in the specific context. Each pair (a_i ; w_i) is called a computational perception item (CPI).

A PM is a tuple (U; y; g; T) where: U is a vector of input CPs, and ui= (A i ,W i ).; y is the output CP, y = (A y ; W y ); g is an aggregation function employed to calculate the vector of fuzzy degrees of validity assigned to each element in y, Wy= (w 1 ; w 2 ;…w), as a fuzzy aggregation of input vectors, Wy= g(W_u1; W_u2;…;W_un), where W are the validity degrees of the input perceptions. T is a text generation algorithm that allows generating the sentences in A.

Example: T is a linguistic template, e.g., “The temperature in the room is ‘high / medium / low’”.

GLMP model present three prototypes, we are interested in the prototype II. (Fig. 3.)

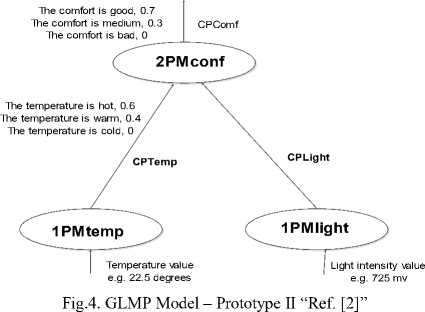
Now, we will proceed to the presentation of our proposed solution which is based on a fuzzy ontology to fill gaps in the GLMP model.

Few times the comfort is good, 0

Few times the comfort is bad, 1

Few times the comfort is medium, 0

Sometimes the comfort is good, 0.3

Sometimes the comfort is bad, 0

Sometimes the comfort is medium, 0.5

Usually times the comfort is good, 0.7

Usually times the comfort is bad, 0

Usually times the comfort is medium, 0.5

CPDayComf

2PMDayComf

The comfort is good, 0.7

The comfort is medium; 0.3

The comfort is bad, 0

CPcomf

The light is high, 0.7

The light is medium, 0.3

The light is low, 0

2PMconf

The temperature is hot, 0.6

The temperature is warm, 0.4

The temperature is cold, 0

CPTemp

1PMtemp

Temperature value

CPLight

1PMlight

Light intensity value e.g. 725 mv

Fig.5. GLMP Model – Prototype III “Ref. [2]”

e.g. 22.5 degrees

• V.    Presentation of our Proposed Approach

Continuing a previous studies for evaluating the imprecision in the decisional requirements expression which one is based on a fuzzy query language “Ref. [41]” and the other is based on belief function “Ref. [42]”, we‘ve limited the study in this paper only to the fuzzy operator of requirements queries. But before presenting our solution, we specify the causes led us to propose a new solution:

• •    GLMP model does not assess the fuzzy requirement even if it is presented in natural language when flexibility is not present in the query predicate value in the sentence adjective.

• •    GLMP model considers only the input of data from databases, but the case of the decisionmaking and the use of the data warehouse are not considered.

• •    Using other ontological models of the literature, we cannot solve the case where the need is more complex and we do not have the possibility to express the need for natural language, which is the most common case in reality and the simplest for decision-makers

• •    The Memon’s algorithm to evaluate the NEAR Fuzzy operator can’t is not enough for us, in fact, we need to treat NEAR Negative only and adapt the NEAR solution which in our case needs other parameters not mentioned by Memon’s solution ”Ref. [30]”. We intend to see other operators, to our knowledge, not studied yet.

Thus, the new proposed solution is fuzzy ontologybased called GLMR “Granular Linguistic Model of

Requirement Ontology – GLMR” Ontology and present two cases (Fig. 2.):

1st Case: “Fuzzy data warehouse”: we have two situations:

* When the attribute concerning the flexible requirements is fuzzy. We will treat this case later.

* Although when the fuzzy attributes don’t concern the flexible requirements, we propose as solution our ontological proposition.

2nd Case: “Non fuzzy Data warehouse”: In our case, the data warehouse is not necessarily vague, also the dimension table is not necessarily fuzzy, (as the solution proposed in “Ref. [33]”. We propose as solution our ontological proposition “GLMR Ontology (Fig. 6.)

The decision need represented in the request form presents a flexible part, in our case, it is about the NEAR-fuzzy operator contained in the request predicate. Before handling this requirement, the user of the transport company's warehouse will load the relevant dataset (for the concerned period) and in order to enrich the query and to evaluate the fuzzy part, he consults the GMLR ontology based on the parameters provided by the transport expert. Once the information processed by the ontology reasoner, already conceived and implemented, we will have as result, RM (Requirement mapping) and O-CPR (Operator- Computational Perception of requirement), which allows us to assign each acquired value to one or more predefined classes with membership degree for each predefined class, so that we can respond to the request and satisfy the decision need. Our proposed solution presents three actors: the decision maker, the user, the expert in addition to the ontology designer who can only be the user of the framework. As support, we use the GLMR ontology, the data warehouse from which we load our dataset, a pc and a means of transmission between user and the decision maker or between the expert and user. As shown in fig.6

In the beginning, we have as input the dataset (the corresponding data in the semester) taken from the data warehouse of the transport company for which, we want to classify the bus company according to the risk type of each, bus. Once, the data set the request of the decision need loaded. We also collect some parameters relating to the road transport risks from the road expert (pv1, pv2). (Fig. 6.)

The GLMR ontology is used to evaluate the inaccuracy present, in this case, at the operator level, using the NEAR- algorithm. Once the processing is done, we will have the CPR_BRTypes corresponding to the acquired data from the transport expert. These outputs of the kind f(D i , I i , MD i ), which allows the user to classify all the acquired data and which he transmits them to the decision-maker for decision making.

First, we study the GLMP model to define our proposal model called GLMR model and this for many reasons: The most important reason firstly is that unlike all existing fuzzy ontology solutions that only process linguistic ontologies, the GLMP model allows us to extend it for representing canonical and non-canonical ontologies of the onion model “Ref. [43]”. On the other hand, the requirement expression is generally in natural language which GLMP ontology is based on. Finally, GLMR model allow us to represent OLAP queries, whereas GLMP does not intend to represent. Here, some differences between the two models:

No

DW is Fuzzy

The proposed GLMR Ontology Granular Linguistic Model of a Requirement Ontology The new concepts non present in GLMP model:

Operator - Computational Requirement Connector - Computational Requirement Fuzzy Rules of Requirement Mapping The validity degree W

he attribute concernin the flexible requirement is Fuzzy

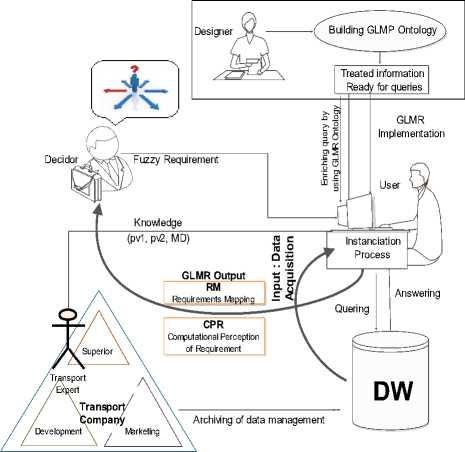
Fig.7. System Architecture

Fig.6. The proposed GLMR Ontology solution

GLMP Model	GLMR Model
1. The Dimension Table is Fuzzy	1. The Dimension Table is not necessary Fuzzy
2.Treat the representation of expert’s knowledge	2.    Treat   the    decider’s requirements
3. Computational representation use only a natural al language	3. Requirements Queries are not necessary written in natural language
4. Imprecision is present in the text representing expert’s perception.	4. Requirement queries containing the fuzziness at the predicate value, connector or operator or other part.
5. GLMP model don’t support the OLAP Query clauses	5. GLMR model support the OLAP Query clauses
6. Represent the perception model	6. Represent the requirement model
7. GLMP allow to construe second order perceptions	7. GLMR allow to construe second order requirements
8. INPUT Values provided by a temperature sensor or by database	8. INPUT Values  provided  by  data warehouse.
9. OUTPUT Generate sentences describing this value	9. OUTPUT Matches the value in input to a class with a degree of belonging

The GLMR model is none other than the GLMP model for the case where the requirement query predicate value is flexible. Our model support the flexible decisional requirements, by adding new concepts: (Table 5). This model also allows us to expand query responses by using semantics derived from ontology as we have already seen in an old paper with XML Databases “Ref. [44]”.

• A.    Computational Perception of Requirement - Operator case:

It is called O-CPR (Operator - CPR) which define the operators between linguistic terms c. O-CPR (E, B, O, L), where O: Fuzzy Operator; E = (e 1 , e 2 , ….. , e n ) is a vector of predicates or linguistic expressions (words or sentences in NL or in Pseudo or in SQL language) that represents the whole linguistic domain of the CPR. Each ei describes the CPR value in each position with specific degree of granularity. These sentences can be either easy, as a= "The temperature is NEAR 18" or more complex, e.g., a = "Sometimes the room temperature in NOT NEAR 25"; W = (w 1 ,w 2 ;…., w n ) is a vector of validity degrees w i [0; 1] assigned to each e i in the specific context. The concept of validity depends on the application, e.g., it is a function of the truthfulness and relevance of each sentence in its context of use.

• •    The fuzzy rules employed by RM can be defined using the membership degree of Target Attribute of model defined in “Ref. [9]”: µ(TA) = MD[0;1]

• •    The sentence in GLMP model can be replaced by a query predicate in GLMR model.

Example: The Bus Risk Type is ‘Acceptable” can be replace by the query: “BRType is Acceptable” or “BRType = Acceptable”.

• •    The input perceptions validity degrees W in GLMP model which represent the validity degrees of flexible requirement in GLMR model where each degree represent the degrees of belonging to a Fuzzy class.

In this paper and for simplification reason, we introduce our solution GLMR and we satisfy with the case where the fuzzy occurs at the operator level.

The target attribute in the query (sentence) containing the fuzzy operator comes in two forms: Number or Date. In this study, we will treat the number case only.

In fact the preceding scheme, we used the following component:

• •    Operator-Computational      Perception      of

Requirement

(O-CPR)):

The Calculation Perception operator uses the fuzzy operator algorithm either NEAR or NOT NEAR Algorithm. O-CPR is the quadruplet (E, B, O, L) where: A (a1,….,an) is the present target attributes when the operators are flexible. B (B = OP2) fixed predicate value(s) O (o1, o2......, on) is the target operator (OP), in this case it is either “NEAR” or “Not NEAR” and with the validity degree MD.

Example:

Select * from Bus where D near 9 AND I Near 14

• •    Operator - Requirement Mapping (O-RM)):

We used RMs to create and aggregate CPRs. There are many types of RMs.

O-RM is a triplet (U, Y, T) where:

U: is an input of RM (Z = A, B, MD (MD-k, k = 0.2))

Y: release of O-CPR ; TO: NEAR Algorithm processing

• •    NEAR- Algorithm

The calculation procedure adds margins to the predicate value PV, m1 and m2 using “(2), (3)” and using “(4), (5)” with pv = op2.

The algorithm computes the values on side using “(6)” with md: membership degrees (initially 0.8) starting from the calculation of diff1 and diff2 using “(8), (9)” wherein m 1 , m 2 are pv margins

The algorithm compares the values of TA (ie: attributes) by the elements defined from m_left to pv. If the range is empty the algorithm adds 0.2 to md and recalculates the margins.

In difference to the solution given by Memon in “Ref. [30]”, which gives as solution the interval [ m _ left , m _ right ]  , the solution in our case is

[ m _ left , PV ] , it is rather the

NEAR NEGATIVE solution. In future work, we will improve this solution to use the Skyline “Ref. [31]” operator algorithms. We present before a comparison between our model and the GLMP one. (Table 5).

So, the global scheme of the proposal solution is as following:

Concept in GLMP Model	Concept in GLMR Model (Operator case)
CP          (Computational Perception) CP (A,W) A = (a1, a2,…..,.an) is a vector of linguistic expressions (words or sentences in NL) Predicate value is a fixed value As “hot” in the sentence – Temperature is “hot” W = (w 1 , w 2 ; …., w n ) is a vector of validity degrees wi [0; 1] assigned to each ai in the specific context. CP Doesn’t exist Doesn’t exist CP Item : (a i ,w i )	CPR (Computational Perception of Requirement) CPR(E,F, W, L, α) E= (e 1 , e 2 ,…..,.e n ) is a vector of requirement query predicates or linguistic expressions (words or sentences in NL or in SQL or in Pseudo code) F = (f 1 ,f 2 ,…,b n ) is a vector of predicate values (Fixe values for the fuzzy operator case , fuzzy value  for the  fuzzy query predicate value case); W=(w 1 ,   w 2 ;   ….,   w n ) = MD=(MD 1 , MD 2 ; …., MD n ) is a vector of validity degrees w i [0;1] assigned to each e i for different case. V-CPR (Predicate Value) O–CPR (Operator) (Fuzzy   Operator   such   as “NEAR” or “Not NEAR”) L (m_left) is a vector of obtained values m_left after evaluation algorithm application of the NEAR fuzzy operator C–CPR (Connector) (Fuzzy Connector such as “and if possible”) α (Mu1,Mu2) will be treated later CPR Item : ((pv i ,w i ),.., (pv j ,w j ))
PM (U, y, g, T ) U is a vector of input CP s, U = (u1 , u2 , . . . , un ) y is the output CP g is an aggregation function employed to calculate the vector of fuzzy degrees of validity assigned to each element in y g is implemented using a strong fuzzy partition of trapezoidal     membership functions. T    is a text generation algorithm    that    allows generating the sentences in Ay PM Doesn’t exist Doesn’t exist	RM (Requirement Mapping) RM (Z ,y ,g , P) Z is a vector of input CPRs, U = (u1 , u2 , . . . , un ) y is the output CPR g is an aggregation function employed to calculate the vector of fuzzy degrees of validity assigned to each element in y g is implemented using a a strong fuzzy partition of triangular membership functions. P is a processing algorithm that asses the fuzzy connector or the fuzzy operator (P=T for the fuzzy predicate value) P-RM (Predicate Value) Connector-RM(Will be studied later) Operator – RM
	Memon & al.[24] seek to identify the interval m_left, m_right while we’re looking only for the value m_left to determine the interval m_left, pv

For the case of Requirement Mapping and especially for evaluating the fuzzy operator, it is proposed to have as input TA target attribute (attribute existing in a predicate including a fuzzy operator), a fixed value B in general, a fuzzy operator (NEAR in our case) and an initial value of membership degree MD (In our case MD = 0.8). Thus, after the NEAR Fuzzy Operator algorithm application, the result in the output will be the interval m1, m2 or m1, PV which is the operator validity range with a validity degree.

Fig.8. Global Scheme of our GLMR Ontology

The NEAR algorithm (Fig. 9) for the NUMBER data type is adapted to our solution as follows:

* The margin to the pv (predicate value), i.e. ml is added dynamically on left side, considering the value it contains. This is performed with the help of the formulae (9) for left side of the scale using “(4) , (5)” wih op2=pv

* The NEAR- operator is supposed to obtain the value NEAR to the pv, thus the target membership degree (md) is initially set to 0.8.

* Values till md are calculated on both the sides with respect to the margin added to pv, with the help of the formulae (6) where, md = membership degree (0.8 initially), starting from the calculation of diff1 using “(8), with op2=pv and ml is pv margin

* The algorithm compares the opl (column) values row by row, till the end of the table, to the elements of the set that NEAR- defined, i.e. value from m_left to pv, adding matching tuples to the result set.

* It is possible that the result set is empty since no values within the range exist in opl. The algorithm checks for empty result set, and in that case, decreases the target md by 0.2 and jumps to step 3. This is the reason big margins to the pv are added.

* In case there are no values in op l that are between ml and pv (and thus the result set is empty), the algorithm fetches the two Nearest values (tuples) to pv, one on each side, as the result.

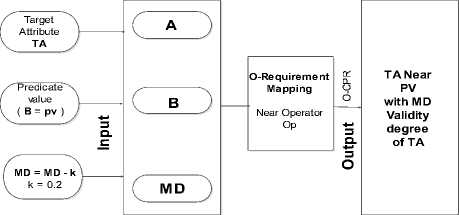
Fig.9. Operator Requirement Mapping

The algorithm returns an empty result only if the table referred to the query is empty. The graph in Fig. 5 depicts the working of NEAR- operator for NUMBER data type (Fig 9).

• B.    Illustrative example

We can simplify these rules after consultation with the road transport expert by eliminating the number of accidents parameter with the consideration in the study only of cases where the accidents number is at most 2 and ignoring some parameters such as the climate parameter or the condition roadway parameter. It is therefore satisfied to a two-Parameter solution model3,4 (the dead number D and injured number I). The proposed rule is:

R1 (Risk Type is Unacceptable): (Deaths NEAR- pv_D AND Injured NEAR- pv I ) OR (Deaths >=pv D AND Injured >= pv I )

The second predicate is automatically executed since it does not include any flexible values.

Decisional requirement: The decider want to have the list of inacceptable Bus in the semester.

Select * from Bus where BRType=”Inacceptable”

For our illustration example, we have Brtype is the type of risk of the bus that can take values {Inacceptable_Bus, Unwanted_Bus, Negligible Bus, Acceptable_Bus}

Rule 1: Per period of time:

It can be seen that the request has a flexible part in the predicate value but by the application of rule 1, the: fuzziness will be present in the operator as:

Select * from Bus where D~9 AND I~14

• • CPR (Computational Perception of Requirement):

O-CPR(E, F, W, L)

E= {e 1 ,e 2 ,?en}={(a 1 ,b 1 ), (a 2 ,b 2 ),?.,(an, bn)} (10)

For our case:

E= {e 1 , e 2 }={(a 1 ,b 1 ),(a 2 ,b 2 )} e 1 =d 1 NEAR- pvD  AND I 1 NEAR- pvI

4          V-----------'              X          V a1

= d 1 NEAR- 9 AND I 1 NEAR- 14

e2 = d2 NEAR - pvD AND I2 NEAR - pvI

X_________________V                J             '_________________V a2b2

F= {pvD, pvI,?pvr}= {pvD, pvI}  ={10,15}(13)

L= {m_left 1 , m_left 2 ,? m_lef tr } = {m_leftD , m_leftI} (14)

MD= W= {MD1, MD2,?.,MDr}= {MD1,MD2}(15)

There are four possible solutions (18):

dlNEAR- pvD ANDI1NEAR- pvlc dl NEAR- pvD AND II NEAR- pvl

-dlNEAR- pvD ANDI1NEAR- pvl dlNEAR-pvD ANDI1"n5^* pvl

MDI = | ⁽ c - m^1)/(Pv - m 1) If m1 <= c <  Pv (16) [        0            If pv <  m l

We note that C may take as appropriate the value of pv D or pvI and clarify this solution we‘ve suppose this following rules example:

R1: BRType = Unacceptable_bus О deaths Number is close to 9 AND the injured number is close to 14).

R2: BRType = Unwnated (Unsafe) bus О Deaths Number is close to 5 AND Injured number is close to 5).

The system behavior, when a flexible query is executed in the system, is analyzed in this case. Part of the DW for the semester period is developed and used for experimental purposes only.(Fig. 10)

The flexible query is:

Select * from Bus where BRType=”Inacceptable”

"The decision maker requirement want to know, in a specific period of time, the company buses "at risk" (Unacceptable, Unsafe, etc.)" implies using the rules given by the transport expert:

Select * from Bus where nb_deaths is NEAR- 9 AND nb_injured is NEAR- 14

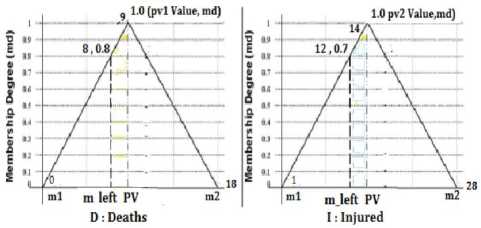
Fig.10. Initial margin target of NEAR Negative Operator (Number case)

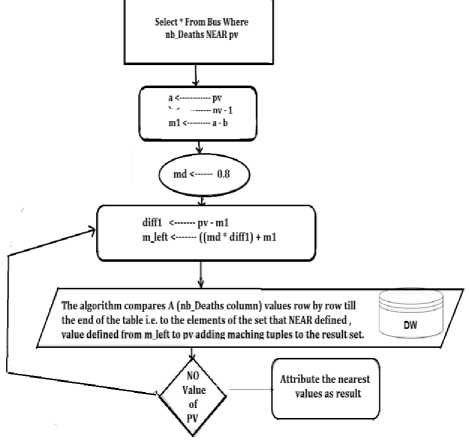
Fig.11. NEAR- - Fuzzy Operator Algorithm

By NEAR- Fuzzy Operator Algorithm application, we’ll have:m_left D <=nb_death<=pv D and m_leftI<= nb_injured <= pvI. So, the query will be:

Select * from Bus where nb_deaths is between (m_leftD AND pvD) AND nb_injured is between (m_leftI AND pvI)

We can thus calculate the belonging degree to the different classes.

• C.    Experimentation of the illustrative example

We’ve create our simple DW at the ontology editor Protégé and then populate it with few examples given by the transport direction then we’ve define all fuzzy concepts at the GLMR ontology before loading the DW concerned part, at our java application to address the imprecision in the decision-making requirements and especially in the operator part.

In this illustrative example, a bus with at least 2 accidents causing at least eight deaths and at least 12 injuries is considered a risk bus (unacceptable bus).

Therefore R1 (bus risk Type is unacceptable): the deaths number NEAR- 10 and the injuries number NEAR- 15 is interpreted by our ontological solution as follows,

R1: D = [8, 10] and I = [12, 15]. The values for D>10 and I>15 belong automatically to the desired class.

Example 1: We suppose having a deaths number is either 9 or 5 and respectively an injured number is 14 or 10 and we and we will study the couple membership to the Inacceptable Bus class for d 1 ={9,5} and I 1 ={14,10}.

Table 6. CPRI Calculation of company Buses for Inacceptable bus class

Bus Class Inacceptable Query Select * from Bus where BRType=”Inacceptable” i.e. Select * from Bus where nb_deaths is close to 9 AND nb_injured is close to 14 Hypotheses D=9 ; I=14 ; a=pv ; b=pv-1 ; m1=a - b where pv=pvD =9 or pv=pvI= 14 Diff1 = a - m1 (diffD, diffI) ; diffl = pv - ml Rewritten query using GLMR ontology Select * from Bus where nb_deaths is between (m_leftD AND pvD) AND nb_injured is between (m_leftI AND pvI) GLMR application Results : CPDeaths ; CPInjured ; RMBRtype ^ MDD; MDI ; MD (D AND I)=MIN(MDD, MDI) NEARAlgorithm Application Calculate : m_left= around ((md * diff) + m1 ) DiffD mdD m_leftD DiffI mdI m_leftI Initial Value 8 0.8 13 0.7 1st iteration 8 0.8 7.1~ 7 13 0.7 10.1 ~ 10 2nd iteration 8 0.6 5.8 ~ 6 13 0.5 7.5 ~ 8 3rd iteration 8 0.4 4.2 ~ 4 13 0.3 4.9 ~ 5 4th iteration 8 0.2 2.6 ~ 3 13 0.1 2.3 ~ 2 Result In case there are no values in A (Nb_deaths , Nb_injured) that are between ml and pv (and thus the result set is empty), the algorithm fetches the Nearest value (tuple) to pv as the result. : m_leftD=7(Found value); m_leftI =12(Nearest value) Degree membership 0.8 0.7 mdD = (7-1)/(10-1) = 6/9 = 0.67 mdI = (12-1)/(15-1)= 11/14 = 0.79 MD = MIN (mdD, mdI) = 0.67 Hypotheses D=4 ; I=10 NEAR- Algo. DiffD mdD m_leftD DiffI mdI m_leftI Initial Value 4 0.8 9 0.7 1st iteration 4 0.8 4.2 ~ 4 9 0.7 7.3~ 7 2nd iteration 4 0.6 3.4~ 3 9 0.5 5.5~ 6 3rd iteration 4 0.4 2.6 ~ 3 9 0.3 3.7~ 4 4th iteration 4 0.2 1.8 ~ 2 9 0.1 1.9~ 2 Result m_leftD =4 (Found value) ; m_leftI 8 (Nearest value) Degree membership 0.8 0.7 mdD = (4-1)/(9-1) = 3/8 = 0.373 mdI = (8-1)/(14-1)= 7/13 = 0.54 MD = MIN (mdD, mdI) = 0.37 f1= {11, 13} belongs to “Unacceptable bus” class with MD = 0.75 f2= {4, 10} belongs to the “Unacceptable bus” class with MD = 0.37

Likewise using this solution in the case D=2, I=4

f3= {2, 4} belong to “Unacceptable Bus” class with md=0, Thus: CPRI 1 : f 1 , MD =0.75; CPRI 2 : f 2 , MD =0.37; CPRI 3 : f 3 ,MD =0

Example 2:  for  d 1 ={2,4},  I 1 ={4,4}   , Bus

Class={Unwanted Bus}, we have :

Table 7. CPRI Calculation of company for Unwanted Bus class

Bus Class	Unwanted
Query	Select * from Bus where BRType=”Unwanted” i.e. Select * from Bus where nb_deaths is close to 5 AND nb_injured is close to 5
Hypothese s	D=2 ; I=4 (Input) a=pv ; b=pv-1 ; m 1 =a - b where c=pv D =5 or c=pv=pv I = 10 Diff 1 = a - m1 (diff D , diff I ) ; diff l = pv - m l
NEARAlgorithm Applicatio n	Calculate : m_left=around ( (md * diff) + m 1 )
	Diff D	md D	m_left D		Diff I	md I	m_left I
Initial Value	4	0.8			09	0.7
1st iteration	4	0.8	4.2 ~ 4		09	0.7	3.8 ~ 4
2nd iteration	4	0.6	3.4 ~ 3		09	0.5	3.0
Result	m_left D =3 ; m_left I 7 (Found values)
Degree membership	0.8	0.7		md D = 0 md I = (4-1)/(5-1)= 3/4 = 0.75 MD = MIN (md D , md I ) = 0
Hypothese s	D=4 ; I=4
NEARAlgo.	Diff D	md D		m_left D	Diff I	md I	m_left I
Initial Value	4	0.8			9	0.7
1st iteration	4	0.8		4.2 ~ 4	9	0.7	3.8 ~ 4
2nd iteration	4	0.6		3.4~ 3	9	0.5	3.0 ~ 3
3rd iteration	4	0.4		2.6 ~ 3	9	0.3	2.2 ~ 2
4th iteration	4	0.2		1.8 ~ 2	9	0.1	1.4 ~ 1
Result	m_left D =4 (Found value) ; m_left I 4 (Nearest value)
Degree membership	0.8	0.7		md D = (4-1)/(5-1) = 3/4 = 0.75 md I = (4-1)/(5-1)= 3/4 = 0.75 MD = MIN (md D , md I ) = 0.75

For the “Unwanted Bus” class , we have f1= {11, 13} belongs to “Unacceptable bus” class with MD = 0 f2= {4, 10} belongs to the “Unwanted bus” class with MD = 0.75 F3={2, 4} belongs to the “Unwanted Bus” class with MD = 0 F4= {4, 4} belong to this class with md=min(0.75, 0.75)=0.75 Thus : CPRI1 : f1, MD =0 ; CPRI2: f2, MD =0.75 ;

CPRI 3 : f 3 , MD =0 ; CPRI 4 : f 4 , MD =0

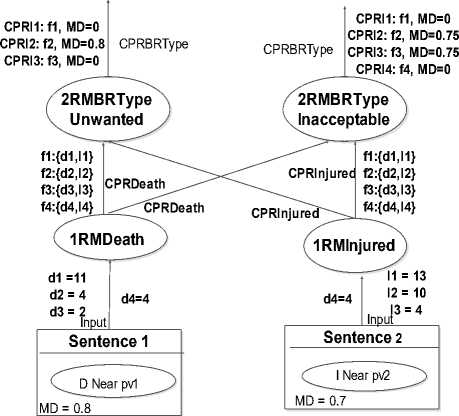
Fig.12. GLMR Solution for Bus Risk Type Examples

However, there is still a lot of work to do, for generalizing this solution, to allow evaluation of the flexible parts at the query predicate value, operators including OLAP operators and connectors. The main insight is to enrich querying expression with the inference capability provided by the fuzzy ontology added to the data warehouse. We built our benchmark (data warehouse) representing road traffic accidents in Algeria, observing the actual rates given in the with a 180 bus park and for a period of 06 months, there were 10000 route sheets/semester, aggregated per week ie 1430 occurrences and over 160 accidents, 50 deaths and 600 injured, including 20 concerned bus. After application of our solution for a period of 06 months and for only 20 Buses, we have detected the following results (Table 8):

Although the dataset was not large, the first results are very encouraging (Fig. 12.)

Table 8. Outcome of the results of experimentation

Select Count(BRType) As Bus_Number (Threshold =0.7)
BRType	Bus_Nb	Decision
Inacceptable	10	Must be removed from service
Unsafe	09	Must be sent to the maintenance
Acceptable	03	/
Negligible	06	/
TOTAL	20

This work highlights one of the decision-making requirements in which the expression of these requirements by decision-makers, who are not necessarily computer experts, generates ambiguous, or imprecise requirements that can affect the entire decision-making process. To remedy this problem and considering the importance of this phase and its impact on the whole process, we evaluate the ambiguity and imprecision in this case by considering only a fuzzy ontology-based solution. To illustrate this proposal, it has been applied to transport risk management in using a set of indicators to classify the risk types. We present in this paper our proposed GLMR model for the NEAR- fuzzy operator, we plan to extend this study to other fuzzy operators such as Not Near- , Far and Large Negative.

There is still a lot of work to do. An extension of this solution is necessary to be able to represent a complex decision-making need by using the ability of this model to break down the need into subparts and to represent each part by a sub-model. Finally, through experimentation it has been found, although the example chosen is simple, that this model can be used to solve real problems.

We can also think of representing this solution in natural language, which is not the case for most of the ontological solutions already proposed. With this solution, we can think of evaluating more complex decisional needs where the fuzzy is present in the operator and the predicate value is not a fixed value such as: NEAR-

Threshold and the threshold is specified by the transport expert, it is found using the ontology. (Which has not been considered by GLMP model) Consideration may be given to another NEAREST operator (closer than) that Memon “Ref. [26]” has not processed and that the GLMR model can solve. (Table 8.).

We plan to study fuzzy OLAP operators such as slice, dice, etc., and use the FMOY fuzzy aggregation function with the "Having" clause that provides the average of an attribute using a membership degree. In addition, we will extend it to fuzzy connectors such as “and possible” and “especially since” connectors that may be present in the decision-making requirement query. In addition, we plan to address uncertainty and incompleteness in needs expressions and apply the solution of our model to other domains. Finally, we consider applying our proposal to a real DW if not a large dataset or a big data.