Fuzzy Pattern Recognition Based on Symmetric Fuzzy Relative Entropy

Published Online October 2009 in MECS

Over the past three decades, a lot of methods have been developed to solve pattern recognition problems. These methods can be grouped into two approaches [1,2,3] : the decision-theoretic and the syntactic approach. The decision-theoretic approach is the most common one. The origin of this approach is related to the development of statistical pattern recognition [4,5]. The goal of statistical methods is to derive class boundaries from statistical properties of feature vectors through procedures known in statistics as hypothesis testing. The hypotheses in this case are that a given object belongs to one of the possible classes. The validity measure used in the decision rule is the probability of making an incorrect decision, or the probability of error. The decision rule is optimal if it minimizes the probability of error or another quantity closely related to it.

Decision-theoretic methods can be classified depending on the representation form of information describing objects and on their application area into three

Manuscript received January 23, 2009; revised June 21, 2009; accepted July 28, 2009.

groups: algorithmic, neural networks-based and rulebased methods [6]. Among algorithmic methods one can distinguish between statistical, clustering and fuzzy pattern matching methods. Clustering methods represent a big class of algorithms for unsupervised learning of structure in data [6-10]. They aim at grouping of objects into homogeneous clusters that are defined so that the intra-cluster distances are minimized while the intercluster distances are maximized.

The desire to fill the gap between traditional pattern recognition methods and human behaviour has led to the development of fuzzy set theory, introduced by L.A. Zadeh in 1965. The fundamental role of fuzzy sets in pattern recognition is to make the opaque classification schemes, usually used by a human, transparent by developing a formal, computer-realizable framework [11]. In other words, fuzzy sets help to transfer a qualitative knowledge regarding a classification task into the relevant algorithmic structure. As a basic tool used for this interface serves a membership function. Its meaning can be interpreted differently depending on the application area of fuzzy sets. A fuzzy pattern matching technique proposed by reference [12] and [13] is based on possibility and necessity measures and aims to estimate the compatibility between an object and prototype values of a class.

The fuzzy pattern matching approach was extended by reference [14] and its general framework summarized by reference [15]. The idea of this group of methods is to build fuzzy prototypes of classes in the form of fuzzy sets and, during classification, to match a new object with all class prototypes and select the class with the highest matching degree. Three semantics of a membership grade can be generalized, according to references [15] and [16] in terms of similarity, uncertainty, or preference, respectively. Fuzzy set theory provides a suitable framework for pattern recognition due to its ability to deal with uncertainties of the non-probabilistic type. In pattern recognition uncertainty may arise from a lack of information, imprecise measurements, random occurrences, vague descriptions, or conflicting or ambiguous information and can appear in different circumstances, for instance, in definitions of features and, accordingly, objects, or in definitions of classes. Different methods process uncertainty in various ways [17-22]. Statistical methods based on probability theory assume features of objects to be random variables and require numerical information. Feature vectors having imprecise, or incomplete, representation are usually ignored or discarded from the classification process. In contrast, fuzzy set theory can be applied for handling non-statistical uncertainty, or fuzziness, at various levels [2326]. Together with possibility theory, it can be used to represent fuzzy objects and fuzzy classes. Objects are considered to be fuzzy if at least one feature is described fuzzily, i.e. feature values are imprecise or represented as linguistic information. Classes are considered to be fuzzy, if their decision boundaries are fuzzy with gradual class membership.

Fuzzy distance measurement, fuzzy similarity measurement and fuzzy entropy are three basic concepts in fuzzy set theory. Fuzzy distance measurement is used to measure the differences between fuzzy sets, and another commonly used concept is the divergence, some of its definitions and applications were denoted in reference [27] and [28].

In this paper, we will study fuzzy similarity degree, entropy, relative entropy, fuzzy entropy and fuzzy relative entropy, and presents novel fuzzy relative entropy, symmetric fuzzy relative entropy, and then we will discuss the applications of the symmetric fuzzy relative entropy in fuzzy spatial object recognition and classification.

• II.    F UZZY SIMILARITY DEGREE , ENTROPY AND SYMMETRIC FUZZY RELATIVE ENTROPY

Throughout this paper, R ⁺ = [ 0, +да ) ; X is the universal set; F ( X ) is the class of all fuzzy sets of X , ^ A ( x ) is the membership function of A e F ( X ) ; P ( X ) is the class of all crisp sets of X ; [ a ] is the fuzzy set for which p A ( x ) = a , V x e X , F is the subclass of F ( X ) with

• (1)    P ( X ) c F ,

  
  
  
  

  e F ,

  
  

• (3)    A , B e F о A и B e F , A c e F , where A c e F is the complement of A e F , i.e.,

^ A ( x ) = 1 - p A ( x ) = 1 - a , V x e X .

Definition 1

A real function, e : F ( X ) ^ R ⁺ is called the entropy on

F ( X ) , if it has the following properties:

(E1) e ( D ) = 0, V D e F ( X ),

(E2) e

= ^maxAe f ( x ) ^e ( A ) ,

(E3) e ( A * ) < e ( A ) , for any sharpening A * of A , (E4) e ( A ) = e ( A c ) , V A e F ( X ).

Where R ⁺ = [ 0, да ) , A c is the complement of A , and A * is the sharpening of A . To express entropy function explicitly, distance measurement is needed. Next, we would define distance measure.

Definition 2

A real function, d : F ² ^ R ⁺ is called the distance measure on F ( X ) , if it satisfies the following properties:

(D1) d ( A , B ) = d ( B , A ), V A , B e F ( X ),

(D2) d ( A , A ) = 0, V A e F ( X ),,

(D3) d ( D , D C ) = max AB _e f ( x ) d ( A , B ),

V D e P ( X ), V A , B e F ( X )

(D4) V A , B , C e F ( X ), if A c B c C , then

d ( A , B ) <  d ( A , C ) and d ( B , C ) <  d ( A , C ).

Similarity degree can be expressed as the complement of distance measurement, the definition of similarity degree is illustrated as follows.

Definition 3

A real function, h : F ² ^ R ⁺ is called a similarity degree on F ( X ) , if it has the following properties:

• (S1)    h ( A , B ) = h ( B , A ), V A , B e F ( X ),

• (S2)    h ( A , A c ) = 0, V A e F ( X ),,

• (S3)    h ( D , D ) = max AB e f ( x ) h ( A , B ),

V D e P ( X ), V A , B e F ( X )

• (S4)    V A , B , C e F ( X ), if A c B c C , then h ( A , B ) >  h ( A , C ) and h ( B , C ) >  h ( A , C ).

The above definitions are axiomatic, and there is an one–to-one relation between all distance measurements and all similarity degrees [29], d + h = 1.

Fuzzy similarity degree is a measure of the closing degree of two fuzzy sets and it is usually used to fuzzy pattern recognition and fuzzy pattern classification.

Supposing     A = ( ^ A ( x 1 ), ^ A ( x ₂),L, ^ a ( x_n ) )     and

B = ( ц _в ( x 1 ), ц _в ( x ₂),L, ц _в ( x_n ) ) are two known fuzzy vectors, then the fuzzy similarity degree of the two fuzzy sets A and B are defined as follows [6]:

Definition 4

§(A , B ) is the fuzzy similarity degree of two fuzzy sets A and B , 3(A , B ) satisfies the following properties:

(FS1)0 <  3(A , B ) < 1, and 5 (Q, 0) = 0.

(FS2) 3(A , B ) = 1 о A = B , 3(A , B ) = 3(B , A ).

(FS3) A c B c C о 3(A , C ) <  5 ( A , B ) л 5 ( B , C ).

• (FS4 ) The larger of 3( A , B ) , the closer of the two fuzzy sets A and B .

There are many definition expressions of the fuzzy similarity degree [6, 31], one of them is the Max-min fuzzy similarity degree and it is defined as following:

Ё min [ Ba ( xi) , Bb ( xi )]

* ( A, B ) = -1 ----------------------- (1)

Ё max [ B a ( x ) , B b ( x ) ]

Definition 5

The fuzzy entropy as a measure of fuzzy set

A = { x , b a ( x ) } is defined as following:

e ( A ) = H ( A ) + H ( A c ), x e X

n

^{H (} A ) = - K Ё B a ⁽ x jln ( B a ⁽ x ) )

i = 1

Where n is the number of elements in the support of fuzzy set A , and K is a positive constant.

Using Shannon’s function

S(x) = -xInx-(1 -x)ln(1 -x), and from definition 5, the reference [30] simplifies the expression in definition 5 to arrive at the following definition.

Definition 6

The entropy E_DT as a measure of fuzziness of a fuzzy set A = { x , b a ( x ) } is defined as

^Edt ⁽ A ) = k Ё {b a ⁽ x ) In B a ⁽ x i ) ⁱ = 1                                           ⁽³⁾

⁺ ( 1^- B a ⁽ x i ) ) In ( 1^- B a ⁽ x i ) ) }

In probability theory and information theory, the relative entropy (also information divergence or Kullback–Leibler divergence) is a non-symmetric measure of the difference between two probability distributions P and Q .

Definition 7

For probability distributions P and Q of a discrete random variable, the relative entropy of probability distribution Q from probability distribution P is defined as following [32]:

n

Dr e ( P , Q ) = Ё Pi ln P7            (4)

i = 1        Qi

The relative entropy could be explained as: the observer could realize a random variable from the distributed information in the range of P ^ Q, , Where

P_i is the transcendental probability distribution, and Q_i is the distributing after observation.

Here are some characteristics about relative entropy:

(RE1) D_re ( P , Q ) has the character of direction, usually, i.e. D_re ( P , Q ) * D_re ( Q , P ).

(RE2) D re ( P , Q ) > 0.

Although the relative entropy is often intuited as a distance metric, it is not a true metric since it is not symmetric (hence 'divergence' rather than 'distance') and does not satisfy the triangle inequality. So a new measurement for divergence is defined as following:

Definition 8

The divergence of two probability distributions could be defined:

J ( P , Q ) = D_r e ( P , Q ) + D re ( Q , P )              (5)

It is evident that J ( P , Q ) is a kind of measurement to denote the difference of two probability distributions, which has three characteristics as following:

(JD1) J(P, Q) has not the characteristic of direction, which is symmetrical to the two probability distributions. i.e. J(P, Q) = J(Q, P),

(JD2) J ( P , Q ) > 0,

(JD3) J ( P , Q ) = 0 о P = Q .

According to definition 6 and definition 7, the fuzzy relative entropy of two fuzzy sets could be defined as following:

Definition 9

Suppose A = ( b a ( x 1 ), B a ( x ₂),L, B a ( x_n ) ) and

B = ( b _b ( x 1 ), B _b ( x 2 ),L , b _b ( x n ) ) are two known fuzzy vectors, then the fuzzy relative entropy of vector A to B is defined as follows:

r ( A , B ) = L A ( x )lnI ^ A^ x ^ ). I          I B b ⁽ x)

+ ( 1 - B a ( x ) ) ln I l- ^l^x l )

( ^{1 - B} b ^{( x}i )

The expression of definition 7 denotes the divergence of fuzzy vectors A and B, but there is a drawback in (6), i.e., when ba(x) ^[0,1] or Bb(x) ^[0,1] ; then r (A, B) ^ ro . This expression needs to be modified and the revised definition of fuzzy relative entropy formula is as following:

Definition 10

Suppose A = ( b a ( x 1 ), B a ( x 2 ),L , B a ( x n ) ) and

B = ( b _b ( x 1 ), B _b ( x 2 ),L , B _b ( x n ) ) are two known fuzzy vectors, then revised fuzzy relative entropy of vector B and A is defined as:

n

R (A, B ) = Z i=1

⁺ ( 1 ^- B a ^{( x}i ) ) In

B a ^{( x}, )ln

B a ⁽ x ) B a ⁽ x ) + B b ⁽ x ) 2

• ^{1    -} B a ⁽ x )

, f B a ^{( x}i ) ⁺ B b ^{( x}i )

1 -

I 2

It can be seen that (7) does not satisfy symmetry, so we present an improved of fuzzy relative entropy, named symmetric fuzzy relative entropy, which satisfies the symmetry and is defined as following:

S ( A , B ) = R ( A , B ) + R ( B , A )            (8)

It is easy to prove that S ( A , B ) has the following characteristics:

(SFE1) S ( A , B ) = S ( B , A ), (SFE2) S ( A , B ) > 0,

(SFE3) S ( A , B ) = 0 о A = B .

It can be clearly seen that the symmetric fuzzy relative entropy S(A, B) is a kind of measurement which could measure the divergence of two fuzzy sets, and it has not only a full physical meaning but also a convenient practicability, so it can be used in fuzzy pattern recognition and classification.

Definition 11

n

+ £i MB(X)ln i=1 I

M B ⁽ x i )

M A ⁽ x i )⁺ M B ⁽ x i )

Suppose          W A = ( w A 1 , w A 2 ,L , w A )          and

W B = ( w B 1 , w B 2 ,L, w B ) are two weighted fuzzy relative entropy following [33]:

weight vectors, the can be defined as

⁺ ( 1^- M B ⁽ x i ) ) ^ln

^{1 -} M B ⁽ x i )

1 -f M A ⁽ x i )⁺ M B ⁽ x i ) '

I 2

Let B = A c , then m b ( X ) = M A ( X ) = 1 - M A ( X ) , and

F (A. B )=zI i=1

, „       ^wA M A ⁽ X)

w,M ( X ,) In----—------—

A i          ^wA M A ⁽ X ) ^{+ w}B M B ⁽ X )

⁺ ( 1 - ^wA

^{1 - w}A, M A ⁽ X )

( M A ( x ) ⁺ M B ( x i ) ) = 1 2             2 ^,

^{1 -} M B ( x ) = M A ( x i ) .

In this case, the following can be obtained.

S ( A , A c ) = R ( A , A c ) + R ( A c , A )

1 -

wM ⁽ X ) ⁺ w B, M B ⁽ X )

{ (9)

=]l I M A ⁽ x i ^)ln = 1 I

Where w A and w_B e [ 0, 1 ] . It is clear that (9) has a universal meaning.

According (8) and (9), we can get the following expression, which can be used as a measurement to measure the divergence of two fuzzy sets:

S w ( A , B ) = F ( A , B ) + F ( B , A )           (10)

It’s easy to prove that F ( A , B ) >  0 , when and only when A = B ,    F ( A , B ) = 0 . Specially, when

m a ⁽ x i )

+ ( 1 - M A ( x , ) ) Int- UA^

1 - ¹

■n [          1    M ( x i )

⁺ E 1 M A ⁽ x , -^)ln-^ln —i—

I = 1 I             ^{2       1}

W A = ( 1,1,L,1 ) and W B = ( 1,1,L,1 ) , F ( A , B ) could be changed to R ( A , B ) and S _W ( A , B ) change to S ( A , B ) . That is say (10) is the general model of fuzzy relative entropy.

In some special case, the relationship of E DT ( A ) and D ( A , B ) can be denoted as following:

^{1 -} M ⁽ X ) ⁺ (1 ^- M A ^{( x}i ))^ln------;—

1 - ¹

= ² ]l { m a ⁽ X ) ^ln M A ⁽ x)

= 1

⁺ ( 1^- M A ^{( x}i ) ) ^ln ( 1^- M A ^{( x}i ) ) ^{+ ln} 2 }

E dt ( A ) =

k

S ( A , A c ) + kn ln2

Where k >  0 and A c is the complement of fuzzy set A .

Proof :

According to (8), we could have followings:

S ( A , B ) = R ( A , B ) + R ( B , A )

1 ⁿ

= ^{2 x ( - k} )^x -7- E { M A ⁽ X) ^ln M A ^{( x}i ) ^{( k} ) i = 1

⁺ ( 1^- M A ^{( x}i ) ) ^ln ( 1^- M A ^{( x}i ) ) ^{+ ln} 2 }

=—— E„ _T ( A ) + 2 n ln 2

DT

^{( - k} )

From the above expression, we can get the following

=yj

^

i = 1

, M      m ( x )

M ( X ) ln — A—-.A----;—-

Мх Э + МХ /)

expression:

E dt ( A ) =

- 1

k

S ( A , A c ) + kn ln2

⁺ ( 1^- M A ⁽ x i ) ) in

^{1 -} M A ⁽ x i )

1 -f M A ⁽ x i )⁺ M B ⁽ x i )

I 2

Proof is over.

From above, it is evident that the Deluca and Termini entropy E DT ( A ) is a special case of the symmetric fuzzy relative entropy S ( A , B ) , so the symmetric fuzzy relative entropy model presented in (8) can be used as a general measurement in the application of fuzzy pattern recognition and classification.

• III.    A PPICATIONS OF THE SYMMETRIC FUZZY RELATIVE ENTROPY

Here are the examples of fuzzy pattern recognition based on fuzzy similarity degrees and symmetric fuzzy relative entropy.

• Example 1:

There is a spatial object which has seven characteristics parameters ( а, в, X, •, ф, 9, у ) and the value of the characteristic vector is approximately equal to ( 4.3,30,200,55,150,285,3000 ) . The spatial object has five standardized spatial postures and the fuzzy membership matrixes of the seven characteristic vectors for each standardized posture are respectively listed as following:

	f	4.1	4.2	4.3	4.4	4.5 a
	A 1	0.8	0.9	0.9	0.9	0.8
	A 2	0.7	0.8	0.9	0.8	0.7
M =
a	A 3	0.8	0.9	0.9	0.9	0.8
	A 4	0.7	0.8	0.9	0.8	0.7
	V A 5	0.8	0.8	0.9	0.8	0.8 ?
f		280	290	300	310	320A
A		0.8	0.9	0.9	0.9	0.8
A,		0.8	0.8	0.9	0.8	0.8
M. =
*    A 3		0.7	0.8	0.9	0.8	0.7
A 4		0.7	0.8	0.9	0.8	0.7
V A 5		0.8	0.9	0.9	0.9	0.8	J
f		190	195	200	205	210 A
	A 1	0.8	0.9	0.9	0.9	0.8
	A 2	0.7	0.8	0.9	0.8	0.7
M. =
X	A 3	0.8	0.9	0.9	0.9	0.8
	A 4	0.7	0.8	0.9	0.8	0.7
V	A 5	0.8	0.9	0.9	0.9	0.8	J
	f	54	55	56	57	58 A
	A 1	0.7	0.8	0.9	0.8	0.7
	A 2	0.7	0.8	0.9	0.8	0.7
M =
•	A 3	0.8	0.9	0.9	0.9	0.8
	A 4	0.7	0.8	0.9	0.8	0.7
	V A 5	0.7	0.8	0.9	0.8	0-7,

M

f	145	150	152	155	160 A
A 1	0.7	0.8	0.9	0.8	0.7
A 2	0.7	0.8	0.9	0.8	0.7
A 3	0.8	0.9	0.9	0.9	0.8
A 4	0.7	0.8	0.9	0.8	0.7
V A 5	0.7	0.8	0.9	0.8	0.7J

	f	280	285	288 290	295A
	A 1	0.7	0.8	0.9 0.8	0.7
	A 2	0.8	0.9	0.9 0.9	0.8
M =
9	A 3	0.7	0.8	0.9 0.8	0.7
	A 4	0.7	0.8	0.9 0.8	0.7
	V A 5	0.7	0.8	0.9 0.8	0.7J
		2500	2800	3000 3200 3500A
	A 1	0.7	0.8	0.9	0.8    0.7
	A 2	0.8	0.9	0.9	0.9    0.8
M =
Y	A 3	0.8	0.9	0.9	0.8    0.8
	A 4	0.7	0.8	0.9	0.8    0.7
	A 5	0.7	0.8	0.9	0.8    0.7 J

Now there are two spatial object B and C , the fuzzy memberships, i.e., the characteristic vectors of them are as following respectively:

a =

fa : 4.1

V ц : 0.8

4.2  4.3 4.4 4.5 A

0.9 0.9 0.9 0.8 J

„  fв:  280  290  300 310320

=

B  (ц;  0.8   0.9   0.9   0.90.8 w  fX;  190  195  200  205210

X =

B   (ц;  0.7  0.8   0.9   0.80.7

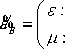
0.8

54 55 56 57 A

0.9 0.9 0.9 0.8 ^J

„ f ф ; 145 150 152 155 ф =

V ц ; 0.7 0.8 0.9 0.8

160 a

0.7 ^J

ж  f 9;  280  285  288  290295

9 =

B  (ц;  0.8   0.9   0.9   0.90.8

„  fу;  2500  2800  3000  32003500

Y =

B   (ц;   0.8    0.9    0.9    0.90.8 and

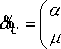
4.1

0.7

4.2 4.3 4.4 4.5 A

0.8 0.9 0.8 0.7 ^J

„   f в;  280  290  300  310320

%' =

C  (ц;  0.8   0.9   0.9   0.90.8 f X;  190  195  200  205210

X =

C (ц;  0.7  0.8  0.9  0.80.7

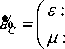
0.8

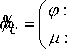
0.8

54 55 56 57 A

0.9 0.9 0.9 0.8 ^J

150 152 155 160 A

0.9 0.9 0.9 0.8J ж  f 9;  280  285  288  290295

9 =

C  (ц;  0.7  0.8  0.9  0.80.7

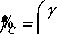
V ц ^;

2500 2800 3000 3200 3500 A

0.7    0.8    0.9    0.80.7

Which postures of the spatial objects B and C may belong to?

Based on (1), the fuzzy similarity degrees of spatial objects B and C to the five standardized gestures are as following:

5( A 1 , B ) = 0.9569,

3( A 2 , B ) = 0.9727, 3( A 3 , B ) = 0.9468, 3( A ₄, B ) = 0.9317, 3( A 5 , B ) = 0.9461;

and

5( A 1 , C ) = 0.9454 ,

5( A 2 , C ) = 0.9454, 5( A 3 , C ) = 0.9461, 5( A ₄, C ) = 0.9579, 5( A 5 , C ) = 0.9454.

From the above results, we can get that

3( A 2 , B ) >  5(A 1 , B ) >  5(A ₃, B ) >  3(A 5 , B ) >  3( A ₄, B ) and

5(A ₄, C ) >  5(A ₃, C ) >  5(A 1 ,C ) = 5(A 2 , C ) = 5(A 5 ,C ). So the spatial objects B and C may respectively belong to the standardized posture A ₂ and A ₄ , but the differences between 3(A ₄, C ) and 5 ( A 3 , C ) are too small to distinguish.

Calculating by (7) and (8), we could get the fuzzy relative entropy of the spatial objects B and C to the known postures, and they are as following respectively:

5 ( A 1 , B ) = 0.2001,

5 ( A ₂, B ) = 0.1333, 5 ( A ₃, B ) = 0.2667, 5 ( A ₄, B ) = 0.2667, 5 ( A 5 , B ) = 0.2667; and

5 ( A 1 , C ) = 0.2667,

5 ( A 2 , C ) = 0.2667, 5 ( A 3 , C ) = 0.2000, 5 ( A ₄, C ) = 0.1333, 5 ( A 5 , C ) = 0.2667.

From the above results, we can get that the symmetric fuzzy relative entropy of spatial object B to standardized gesture A ₂ is the minimum, so spatial object B should be in A ₂ pattern. The fuzzy relative entropy of spatial object C to standardized posture A ₄ is also minimum, so spatial object C should be in posture A ₂ . It is clear that the differences between      S ( A ₂ , B )      and

5 ( A , B )( i = 1,3,4,5)       ,         5 ( A 4 , C )        and

5 ( A , C )( i = 1,2,3,5) are much more distinct than the difference of fuzzy similarity degrees.

• Example 2:

There are a number of microbes and they belong to one of the four known microbes, each of them has five features, i.e., perimeter, area, roundness, major axis and minor axis. The feature values of part of these samples are listed in Table 1.

Depending on the experiences, experts’ suggestions and sampling data, we can get the fuzzy memberships of sampling data and parts of them are list in Table 2.

The standard feature values of the four microbes (abbreviation Mb.) are listed in Table 3.

Now, 30 samples of each type microbe are randomly selected from sample database, and the divergence of each selected sample to the standard sample is respectively calculated by fuzzy similarity degree and symmetric fuzzy relative entropy. Each sample could be classified by its divergence value to the standard samples. The results listed in Table 4 and Table 5 are the classified results based on fuzzy similarity degree and symmetric fuzzy relative entropy respectively.

T ABLE 1 T HE FEATURE VALUES OF SAMPLING DATA

Samples	Features
	Perimeter	Area	Roundness	Major axis	Minor axis
1	813	64.78	0.97	35.71	29.56
2	138	31.56	0.89	25.21	7.93
3	859	69.85	0.98	38.86	34.50
4	116	30.55	0.78	16.13	12.02
5	108	22.78	0.42	24.23	12.53
...	...	...	...	...	...
n	...	...	...	...	...

T ABLE 2 T HE FUZZY MEMBERSHIPS OF PART SAMPLES

Samples	Microbe 1	Microbe 2	Microbe 3	Microbe 4
1	0.87	0.74	0.78	0.71
2	0.85	0.86	0.82	0.66
3	0.56	0.77	0.85	0.72
4	0.64	0.54	0.69	0.72
5	0.56	0.92	0.68	0.61
6	0.84	0.61	0.68	0.72
7	0.78	0.67	0.61	0.53
8	0.82	0.68	0.57	0.53
9	0.76	0.90	0.65	0.71
10	0.68	0.56	0.85	0.72
...	...	...	...	...

T ABLE 3 T HE FEATURE VALUES OF STANDARD SAMPLE

	Perimeter	Area	Roundness	Major axis	Minor axis
Mb. 1	850	68	0.98	38.2	30.5
Mb. 2	130	31	0.85	25.1	8.4
Mb. 3	118	29	0.78	151.4	13.1
Mb. 4	102	22	0.43	17.9	9.2

T ABLE 4 T HE CLASSIFICATION RESULT BASED ON FUZZY SIMILARITY

DEGREE

	Mb. 1	Mb. 2	Mb.3	Mb.4
Number of samples	30	30	30	30
Number of judgment	31	31	29	30
Number of false	4	2	1	2

T ABLE 5 T HE CLASSIFICATION RESULT BASED ON SYMMETRIC FUZZY

RELATIVE ENTROPY

	Mb. 1	Mb. 2	Mb.3	Mb.4
Number of samples	30	30	30	30
Number of judgment	31	30	29	30
Number of false	2	1	0	0

It could be seen that there are 9 false classifications in Table 4 and 3 false classifications in Table 5, that is to say, the recognition and classification accuracy based on symmetric fuzzy relative entropy is higher than fuzzy similarity degree.

• IV. C ONCLUSIONS

Fuzzy similarity degree and fuzzy relative entropy are the measures of divergence of two fuzzy sets, they are usually used in fuzzy pattern recognition and classification. But the fuzzy similarity degrees of fuzzy sets may be equals or nearness sometimes, so it is difficult to use it for fuzzy pattern recognition and classification sometimes. The symmetric fuzzy relative entropy presented in this paper has not only clear physical meaning but also practical usage. The examples in section III have shown their applications in fuzzy pattern recognition and classification.

A CKNOWLEDGMENT

The authors wish to thank the referees and the editors for their constructive advice and suggestions. This work was supported in part by the Innovative Foundation of Nanjing Forestry University (No. 163050042).