Галактическое гало темной материи из легких бозонов

Данные наблюдений указывают на то, что около четверти плотности энергии Вселенной приходится на небарионную тёмную материю (ТМ). Ряд теорий предлагает различных кандидатов на роль ТМ, не входящих в Стандартную модель физики элементарных частиц.

С точки зрения космологии предпочтительными являются модели, в которых частицы ТМ были нерелятивистскими при отделении от тепловой среды в ранней Вселенной. Такие частицы образуют холодную тёмную материю (CDM). Наиболее вероятными кандидатами на роль CDM являются слабо взаимодействующие массивные частицы (WIMP). WIMP естественным образом создают современную остаточную плотность тёмной материи, а моделирование с использованием метода N-тел воспроизводит основные свойства крупномасштабных структур. Однако при применении к малым масштабам возникают трудности.

Значительной проблемой для модели WIMP является наличие центрального пика в профилях плотности гало. Моделирование показывает, что вблизи центра плотность изменяется по закону ρ ∝ r ^{- 1} , в то время как наблюдения указывают на более плавное распределение плотности. Кроме того, прогнозируемое количество карликовых галактик значительно превышает наблюдаемое [1].

Другими кандидатами на роль частиц CDM являются легкие бозоны в широком диапазоне масс m ∼ 10 ^{- 24} - 10 ³ эВ. Темная материя из этих частиц исследовалась преимущественно в состоянии бозе-эйнштейновского конденсата [2, 3].

В данной работе рассматривается модель, в которой частицы находятся вблизи критической точки конденсации, но еще не перешли в вырожденное состояние.

• 1. Гало темной материи из бозе-газа

Рассмотрим гало темной материи из легких бозонов, которые находятся вблизи критической точки бозе-эйнштейновской конденсации, но еще остаются в невырожденном состоянии. В таком случае плотность частиц можно получить интегрированием стационарного распределения Бозе-Эйнштейна [4]:

n ( r ) = / (2 dnp 3 卜*° ( r ) - " - 1 i 1 = 》 - B g 3 / 2 ( z ( r )) ,                       (1)

где AdB =，2n%2/mkT - длина волны де Бройля и g3/2(z) является частным случаем поли-∞i логарифмических функций gs(z) = ^^ 彳 (иногда g3/2(z) также обозначается как функция Бозе-i=1

Эйнштейна), а ее аргументом в (1) является

z ( r )

e ( µ - m Φ( r ) - 2 gn ( r )) /kT

где µ - химический потенциал, g - константа связи, определяющая взаимодействие между частицами, а гравитационный потенциал Ф( г ) подчиняется уравнению Пуассона

▽ ² V ( r ) = 4 nGmn ( r ) .

Применяя оператор набла к (1) и используя уравнение (3), получаем

( 1 + аВЪ ^{g 1 / 2 (z)} ) ^v 2 ^n(r) - ^A d^B 1—^ ( ^{V n(r)} ) 2 + ⁴ⁿ §^ ^{g 1 / 2 (z)n(r)} = ⁰.       ⑷

Уравнения (4) и (2) описывают структуру Томаса-Ферми для бозонных гало тёмной материи. Аналогично фермионные гало рассматривались в [5, 6].

Для неконденсированных бозонов самодействие не играет ключевой роли. Его вклад в первый член уравнения (4) составляет порядка 2 g/ ( A dB kT ) 《 1 , и им можно пренебречь без ущерба для дальнейших расчетов [7].

Тогда уравнение (4) можно преобразовать в безразмерное уравнение

R ²

kT

4 nGm ² n o

Параметр ν определяется как

V = AdB no , а величина z в уравнении (5) находится как решение уравнения

Vx = g 3 / 2 ( z ) .

Уравнение (5) содержит единственный параметр ν, выражающий количество частиц в кубическом объёме тепловой длины волны де Бройля в центре гало. Поскольку уравнение описывает неконденсированные бозоны, параметр v находится в диапазоне от нуля до Z (3 / 2) . Значения выше

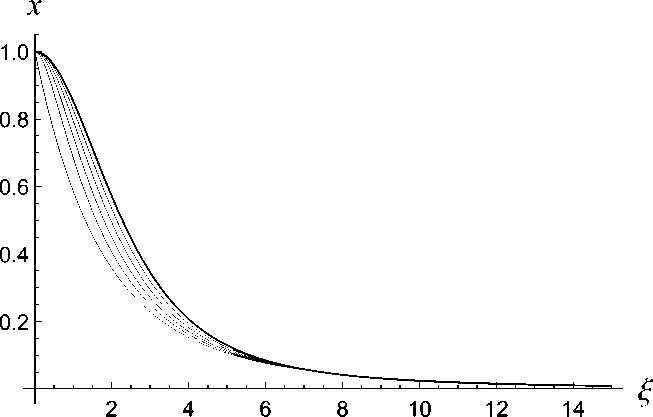
Рис. 1. Профили плотности для гало из неконденсированных бозонов при ν = 0,5, 1, 1,5, 2, 2,61 (от верхней к нижней тонкой линии). Жирная линия соответствует изотермической модели.

этого диапазона соответствуют области конденсации, где уравнение (5) неприменимо. Решения уравнения (5) показаны на рис. 1.

Если параметр v 《 1 , то бозоны находятся далеко от точки конденсации и могут рассматриваться как идеальный газ с распределением Максвелла-Больцмана. В этом случае уравнение (5) сводится к

▽声 - |( V _€ x ) ² + x ² = 0 ,                                (8)

что соответствует модели изотермического профиля.

Изотермический профиль также воспроизводится уравнением (5) при больших £, когда x 《 1 . То же самое справедливо для фермионных гало с распределением Томаса-Ферми [6]. Такое сходство в поведении показывает, что статистика частиц имеет решающее значение внутри ядра галактического гало, в то время как за его пределами темная материя переходит в разреженное состояние, соответствующий классическому газу. Нет единого мнения о том, что следует считать ядром гало. Обычно его рассматривают как область, внутри которой плотность уменьшается в определенное количество раз. В [6] это соотношение принимается равным четырём в соответствии с эмпирическим профилем Буркерта. Следуя тому же выбору, из уравнения (5) можно найти безразмерный радиус ядра ξ _core , зависящий от ν. Соответствующий размерный радиус определяется как

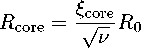
На рис. 2 видно, что радиус ядра ξ _core практически не меняется, так что при фиксированной температуре R _core уменьшается по мере увеличения параметра ν и достигает минимума R _m i _n в критической точке конденсации v = Z (3 / 2) . Ниже этого порогового радиуса плотность частиц в центре гало становится достаточно высокой для перехода в конденсированное состояние. В таком случае конденсированные бозоны образовывают компактные объекты, которые также называют бозе-звездами, в то время как окружающие их частицы остаются неконденсированными, сохраняя соотношение R _core ≥ R _m i _n . Этот механизм поддерживает размер гало выше порогового радиуса и может рассматриваться как подходящее объяснение того, почему галактики меньшего размера встречаются редко, в то время как галактики большего размера встречаются в достаточном количестве.

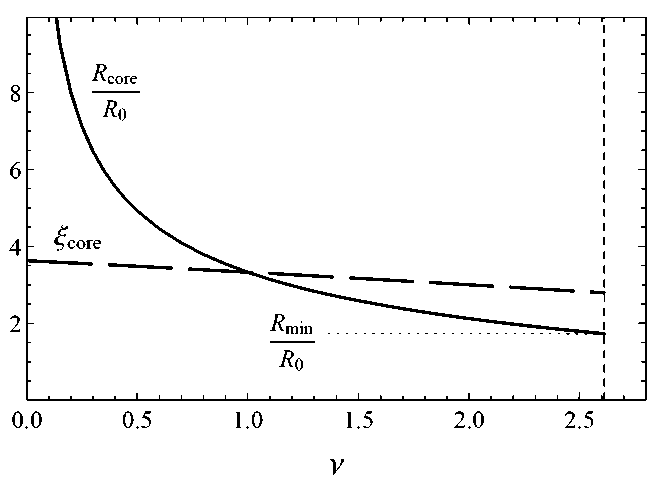
Рис. 2. Безразмерный радиус ядра ξ core (пунктирная линия) и соответствующий размерный радиус в единицах R 0 (сплошная линия) в зависимости от параметра ν.

Заключение

В данной работе проанализировано распределение плотности гало темной материи из невырожденных бозонов. Вблизи критической точки конденсации это распределение отличается от распределения изотермической модели. Радиус ядра такого гало достигает минимума в критической точке.

При конденсации в гало из невырожденных бозонов могут образовываться бозе-звезды, радиус которых зависит от амплитуды рассеяния, но ограничен порядком астрономических единиц. Их вклад можно учесть отдельно с помощью уравнения Джинса. Такая модель темной материи хорошо согласуется с наблюдаемыми кривыми вращения, как показано в работе [7].