Гамильтоновы укорочения ограниченной задачи трех тел

Данная работа посвящена исследованию гамильтоновых укорочений пространственной ограниченной задачи трех тел (далее — ОЗТТ) и пространственной задачи Хилла методами степенной геометрии.

Основная концепция степенной геометрии заключается в изучении нелинейных задач не в исходных координатах, а в логарифмах этих координат. Тогда многим свойствам и соотношениям, нелинейным в исходных координатах, можно поставить в соответствие определенные линейные соотношения. Алгоритмы степенной геометрии основаны на этих линейных соотношениях: они позволяют упрощать уравнения, разрешать их особенности, выделять их первые приближения и находить либо их решения, либо асимптотики этих решений. После одного шага таких упрощающих преобразований можно получить степенные решения или степенные асимптотики решений. После кратного применения этих алгоритмов можно получить решения или их асимптотики, содержащие кратные логарифмы и экспоненты. Этот подход позволяет также вычислять асимптотические и локальные разложения решений. Алгоритмы степенной геометрии применимы к уравнениям разных типов: алгебраическим, обыкновенным дифференциальным и в частных производных, а также — к системам таких уравнений.

Над разработкой методов степенной геометрии работали И. Ньютон, М.М. Вайнберг, В.А. Треногин, С. Лефшец, П.Г. Айзенгендлер, А.Д. Брюно (см. обзор [9], книги [4; 5], статью [2] и указанную в этих работах библиографию). Применение методов степенной геометрии к небесно-механическим задачам выполнено в работах А.Д. Брюно [3; 4; 11].

В 2007 г. в работе А.Д. Брюно и В.П. Варина [3] c помощью методов степенной геометрии найдены все предельные случаи плоской ограниченной задачи трех тел при стремлении массового параметра µ к нулю: задача двух тел, задача Хилла, промежуточная задача Энона и основная предельная задача. В каждой из них выделяются решения, которые являются пределами периодических решений ограниченной задачи трех тел при ^ ^ 0 , и пределы семейств периодических решений (называемые порождающими семействами).

Методы степенной геометрии могут быть эффективно применены к исследованию гамильтоновых систем, при этом достаточно выполнять основные операции степенной геометрии над функцией Гамильтона, а не над системой связанных с ней канонических уравнений. Напомним основные идеи степенной геометрии, следуя [4, гл. I, II, IV].

Пусть z = ( x , y ) G R 2n — вектор фазового пространства, x G R n — координаты, y G R n — канонически сопряженные импульсы, а H ( z ) — функция Гамильтона, аналитическая в точке z ₀ . Тогда она разлагается в ряд Тейлора

H ( z ) = £ H r ( z - z o ) ^R                           (1)

R∈S где R G Z+n — векторный показатель степени, S — некоторое дискретное множество в Z+n — носитель суммы (1), HR G R, сходящийся в некоторой окрестности U точки z = z0. Носителю S разложения (1) соответствует внешняя выпуклая оболочка Г(Н) deef conv S, которую называют многогранником Ньютона. Граница дГ многогранника Ньютона Г(Н) состоит из граней rjd) размерности d, а каждой грани rjd) соответствует граничное множество Sjd , касательный конус T(d) в R2n и нормальный конус Ujd) в сопряженном пространстве R2n. Каждой грани rjd) соответствует свое укорочение ТТ (d)

H _j гамильтониана H , определяемое следующим образом:

H jd = Е H r ( z - z o ) ^R по R G S jd .

R

( d

Оказывается (см. [4, гл. IV]), что не каждое укорочение H _j функции гамильтона H будет гамильтоновым. В работе [11] было предложено находить укорочения функции Гамильтона H так, чтобы они все были гамильтоновы. А именно, каждому векторному показателю R = ( P , Q ) G Z +n , P = (p i ,...,p _n ) , Q = (q ₁ ,..., q _n ) ставится в соответствие точка — проекция n(P, Q) на двумерную решетку Z ² , определяемую по правилу: n(P, Q) def (p, q) G Z ² , где p = ^ П=₁ p i , q = ^ П=₁ q i . На плоскости R ² для проекции nS носителя S строится выпуклая оболочка пГ и для каждой грани y ее границы дпГ находится соответствующее укорочение H γ функции Гамильтона H .

Если гамильтониан H зависит дополнительно от вектора малых параметров M = (^ ₁ , ..., ^ l ) , то разложение (1) производится не только по фазовым координатам z , но и по параметрам M :

H = Е HpqtxP yQMT, где носитель S = {(Р, Q, T) G Z2n+l : HPqT = 0}. В этом случае проектирование п носителя S выполняется в трехмерную целочисленную решетку Z3 по правилу п(Р, Q, T) =f (p, q, t), где p и q определены выше, а t = ^i=1 ti.

Гамильтоновы укорочения Н^ ) — это различные первые приближения гамильтониана H , справедливые в различных областях фазового пространства R ²ⁿ или фазового пространства R ^2n+l , расширенного пространством параметров. Выбор этих областей определяется соответствующим конусом задачи K ∈ R ² _∗ ^n+l , представляющим собой открытый выпуклый конус.

Гамильтониан H можно рассматривать как возмущение некоторой более просто устроенной гамильтоновой системы, определяемой соответствующим укорочением Н j^(d) . Эти укорочения могут быть устроены существенно проще исходного гамильтониана, и, возможно, удастся проинтегрировать соответствующие этим укорочениям системы канонических уравнений и получить начальные приближенные решения полной задачи.

• 1 . Десингуляризация пространственной ограниченной задачи трех тел

Рассмотрим гамильтониан пространственной ОЗТТ, канонические уравнения которого описывают движение частицы пренебрежимо малой массы под действием сил гравитации двух тел, которые равномерно вращаются вокруг общего центра масс по круговым орбитам. Система координат выбрана так, что тяготеющие тела массами 1 — — и — ( — < 1/2 ) расположены в точках ( — —, 0,0) и (1 — —, 0,0) соответственно. Тогда гамильтониан H в безразмерных координатах имеет вид

^{Н ( x} , У ) = ¹⁽У 2 + У 2 + У 3 ) + ^Х 2 У 1 ^{— Х} 1 У 2 ^{— 1}— ^{— —} —,              ⁽²⁾

• 2                                       Р 1       р 2

где

Р 1 = (Х 1 + —) ² + Х 2 + X 2 , Р 2 =   (Х 1 — (1 — —)) 2 + x 2 + X 2 •

Для того чтобы при малых µ найти все первые приближения ОЗТТ вблизи меньшего из двух тяготеющих тел, нужно ввести локальные координаты

• < 1 = X 1 + — — 1,  < 2 = X 2 ,  < 3 = Х з ,  П 1 = У 1 ,  П 2 = У 2 + — — 1,  П 3 = У з

и разложить функцию Гамильтона (2) по этим координатам. После разложения функции где f — сходящийся степенной ряд, не содержащий членов порядка меньше трех. Носитель (S1) ряда в правой части равенства (3) состоит из точек

R = (Г 1 , Г 2 , Г з , Г 4 , Г 5 , Г б , Г 7 ) = (ord( 1 , ord( 2 , ord( 3 , ordП 1 , ordП 2 , ordП з , ordр) :

(0, 0, 0, 2, 0, 0, 0), (0, - 1, 0, 0, 0, 0,1), (2, 0, 0, 0, 0, 0, 0), (0, 2, 0, 0, 0, 0,1),

(0, 0, 0, 0, 2, 0, 0), (0, 0, - 1, 0, 0, 0,1), (0, 2, 0, 0, 0, 0, 0), (0, 0, 2, 0, 0, 0,1),

(0, 0, 0, 0, 0, 2, 0),

(0,1, 0,1, 0, 0, 0),

(0, 0, 2, 0, 0, 0, 0),

(k, 2l, 2m, 0, 0, 0, 0),

( - 1, 0, 0, 0, 0, 0,1), (1, 0, 0, 0,1, 0, 0), (2, 0, 0, 0, 0, 0,1), (k, 2l, 2m, 0, 0, 0,1),

где k, l ^ 0 , k + 2l + 2m ^ 5 и плоскости, соединяющей точки ( — 1,0, 0, 0, 0, 0,1) , (0, — 1, 0, 0, 0, 0,1) , (0, 0, — 1, 0, 0, 0,1) . Эта плоскость — носитель члена р/х 1 + х 2 + х 2 .

Конус задачи будем выбирать так, чтобы укорочения гамильтониана (3) соответствовали малым значениям параметра р и описывали движение тела в окрестности начала координат. Таким образом, конус задачи будет

K = {W G R7 : w1 < 0, w2 < 0, w3 < 0, w7 < 0}, так как (1,(2, (з, м ^ 0.

Построим проекцию nR = R" = (p, q, s) G R3, где p = ri + Г2 + Г3, q = Г4 + Г5 + Гб и s = Г7.

Множество S i ’ этих точек состоит из точек (0, 2, 0) , (2, 0, 0) , (k, 0, 0) , ( — 1, 0,1) , (1,1, 0) , (2, 0,1) , (k, 0,1) , k = 5 , 6 , 7 , ...

Замыкание выпуклой оболочки множества S1’ — это многогранник Г С R3, состоящий из граней Г(2), ребер Г(1) и вершин Г(0). Проекция исходного конуса задачи K есть конус задачи к’’ = { W‘‘ G R3 : W1 < 0, W3 < 0} .

Многогранник Г представляет собой полубесконечную трехгранную призму с косым основанием, которая имеет четыре грани, шесть ребер и три вершины (см. рис 1).

Грань Г 12) служит косым основанием призмы Г , она содержит вершины (0,2,0) , (2, 0, 0) , ( — 1, 0,1) и точку (1,1, 0) . Ее вектор нормали N 1 ’ = — (1,1, 3) G К ’’ . Ей соответствует укороченная функция Гамильтона

H ²) = ¹ (щ ² + П 2 + _%² ) + (^ — (щ — ( 2^! + S + ^{( з} — , ^р ,

1 q \ 1 1       2 з ²¹ 'ъ¹ 2    >>1                            2      2      2 ,

• ^{2                                         2    2}     ^/⁽1 + ⁽ 2 + ⁽ з

которая при р = 1 описывает пространственную задачу Хилла.

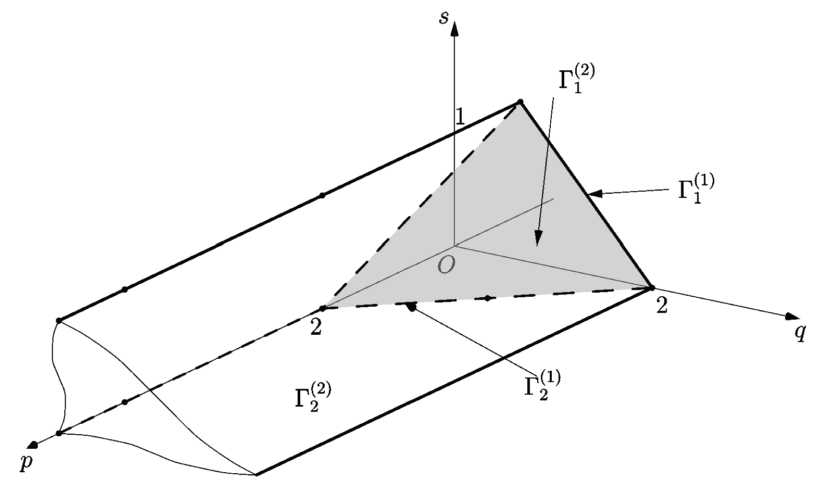
Рис. 1. Проекция многогранника Ньютона гамильтониана (3) ограниченной задачи трех тел

Для малых ^ > 0 вблизи меньшего тела имеется сингулярное возмущение случая ^ = 0 . При ^ ^ 0 объекты ограниченной задачи в координатах X j ,y j стремятся к предельным положениям. При этом для некоторых объектов предельные положения имеют меньшую размерность, чем допредельные. В этом и проявляются сингулярные возмущения. Чтобы устранить сингулярность возмущения при ^ > 0 , надо вводить новые (зависящие от µ ) координаты, в которых размерность предельного объекта равна размерности допредельного. При этом в качестве предельной получается задача, соответствующая первому приближению сингулярного возмущения. Введение таких координат в [3] названо десингуляризацией .

Степенное преобразование

C i = М 1/3 C i , n i = М 1/3 П, i = 1,2, 3

приводит пространственную задачу Хилла к системе с функцией Гамильтона

• 1    _     _           ~       ~       .     C ²     C ²             1

H Hill = - (ⁿ 1 + ⁿ 2 + %) + <^ 2 ^ ^— 1 ⁿ 2 ^— £ 1 + — + —---_  = ■      ⁽⁴⁾

• ^{2                             2 2}    de +C 2 +C 2

Задача Хилла является неинтегрируемой, но имеет многочисленные применения (см., например, [1]), а ее гамильтониан исследован методами степенной геометрии в п. 2.

Грань Г22) содержит вершины (0, 2, 0), (2, 0, 0), (1,1, 0) и точки (к, 0, 0), к = 5, 6,.... Ее вектор нормали N22 = (0, 0, —1) G К’’. Ей соответствует укороченная функция Гамильтона й (2)      1     2,2,2                              2 I C 2 ,  C3 ,           л2 л2\

H2 =2 (n1 + П2 + Пз) + С2П1 — C1n2 — С1 + у + "2" + f (C1,C2 ,C3 ), которая описывает задачу, занимающую промежуточное место между интегрируемой задачей Энона (6) и неинтегрируемой задачей Хилла (4).

Остальные две грани имеют нормальные векторы (0, — 1, 0) и (0,1, 2) , лежащие вне конуса задачи K ^′′ , поэтому соответствующие укорочения гамильтониана не рассматриваются.

Рассмотрим ребра. Из шести ребер одно несобственное. Оно проходит через точку (0, 2, 0) параллельно вектору (1, 0, 0) . На трех ребрах q = 0 , то есть для них укороченная функция Гамильтона не зависит от импульсов n i , i = 1, 2, 3 , и у решений соответствующей системы Гамильтона £ 1 ,£ ₂ ,£ ₃ = const . Остаются два ребра Г 11) и Г 2¹) .

Ребро Г 11) содержит точки (0, 2, 0) и ( — 1, 0,1) множества S". Соответствующая укороченная функция Гамильтона

^ЙР = 1(^{n 2 + n} 2^{2 + n 2 )} - , 2 Л2 , 22 , ²                 VS X ⁺ S 2 ⁺ S 3

которая описывает пространственную задачу двух тел в неподвижной системе координат. Эта задача интегрируема и все ее финитные движения есть периодические орбиты (см., например, [8]).

Пусть Г02) — грань, проходящая через точки (0, 2, 0), (2, 0,1), (—1, 0,1). Ее внешняя нормаль N0’ = (0,1, 2), а вектор нормали к грани Г12) есть N" = —(1,1, 3). Поскольку ребро Г11) — пересечение граней Г02) и Г12), то его нормальный конус состоит из векторов N = (пт,п2,пз) = aN0 + eNI, где а, в > 0. Положим а = в = 1, тогда получаем вектор N = —(1, 0,1), лежащий в нормальном конусе ребра Г11). Ему соответствует степенное преобразование ti = ^ti, ni = МПь t = Mt i = 1, 2, 3, которое приводит к системе с функцией Гамильтона

^2 ^ ^{n 2 + n 2 + n} 2 ) -

.

l ^v            ^v            ^v

V £ +<2 +t3

Эта функция отличается от гамильтониана (5) только коэффициентом м = 1 .

Ребро г 21) содержит точки (0, 2, 0) , (2, 0, 0) , (1,1, 0) множества S". Ему соответствует укороченная функция Гамильтона

^Й 21) = 2 № ^{+ n 2 + n} 3 ) ⁺ £^ 1 ^— £ 1% ^{— t 2 +} у ⁺ у,

которая описывает промежуточную задачу Энона . Название задачи было предложено в работе [3], поскольку ее плоский вариант был подробно исследован М. Эноном (M. He´ non) в работе [12]. Эта задача рассматривалась многими исследователями, в частности, она применялась для построения и исследования квазиспутниковых орбит (см. [6; 7; 10]).

Укорочения, соответствующие вершинам, не являются содержательными, поскольку содержат либо члены, зависящие только от координат, либо члены, зависящие только от импульсов.

Итак, как и в случае плоской ОЗТТ [3], в окрестности меньшего из двух тел имеются три различные десингуляризации, соответствующие грани Г ^²⁾ и ребрам Г 11) и 1)

• Г ₂ .

• 2.    Десингуляризация пространственной задачи Хилла

Рассмотрим гамильтониан пространственной задачи Хилла, который имеет одну особенность в начале координат.

^ннш — 2 ( y ² + y ² + y ² ) ^-

/ _{9    9} =S + ^x 2 y 1 ^{- x} 1 y 2 ^- ~ ( ^2x 1 ^{- x} 2 ^{- x} 2 ) .

x 2 + x2 + x 2                  2

Перейдем в пространство показателей степеней и построим носитель S1 правой части равенства (7). Он состоит из точек

R — (г 1 , r ₂ , r ₃ , r ₄ , r ₅ , r ₆ ) — (ord x 1 , ord x ₂ , ord x ₃ , ord y 1 , ord y ₂ , ord y ₃ ) :

(0, 0, 0, 2, 0, 0),      (0, 0, 0, 0, 2, 0),      (0, 0, 0, 0, 0, 2),   ( - 1, 0, 0, 0, 0, 0),

(0, - 1, 0, 0, 0, 0),   (0, 0, - 1, 0, 0, 0),   (0,1, 0,1, 0, 0),   (1, 0, 0, 0,1, 0),

(2, 0, 0, 0, 0, 0),      (0, 2, 0, 0, 0, 0),      (0, 0, 2, 0, 0, 0)

и из плоскости, соединяющей точки ( - 1, 0, 0, 0, 0, 0) , (0, - 1, 0, 0, 0, 0) , (0, 0, - 1, 0, 0, 0) . Эта плоскость — носитель члена 1 Д/x l + x 2 + х 2 . Рассмотрим два конуса задачи. Первый конус задачи K 1 определим так, чтобы укорочения гамильтониана (7) описывали движение тела в окрестности начала координат:

K1 — {W € R6 : w1 < 0, w2 < 0, w3 < 0}, так как x1,x2,x3 ^ 0. Второй конус задачи K2 определим так, чтобы укорочения гамильтониана (7) описывали движение тела вдали от начала координат:

K2 — {W € R6 : w1 > 0, w2 > 0, w3 > 0}, так как x1, x2,x3 ^ to.

Построим проекцию nR — R’’ —f (p, q) € R2, где p — ri + Г2 + Г3 и q — Г4 + Г5 + r6.

Множество S 1 ‘ этих точек R ’’ состоит из (0, 2) , ( - 1, 0) , (1,1) , (2, 0) .

Замыкание выпуклой оболочки множества S 1 ’ — это многоугольник Г С R ² . Граница дГ многоугольника Г состоит из ребер Г ⁽¹⁾ и вершин Г ⁽⁰⁾ (см. рис. 2). Каждому такому элементу r ^(d) соответствует укороченный гамильтониан H^d, являющийся суммой тех членов (7), точки которых R^M € r ^(d) . Укороченные функции гамильтониана H^d — это различные первые приближения функции (7), справедливые в разных областях фазового пространства R 6 . Конусы задачи есть K 1 — { W ‘‘ € R ² : w 1 < 0 } и K 2 — { W ‘‘ € R 2 : w i > 0 } .

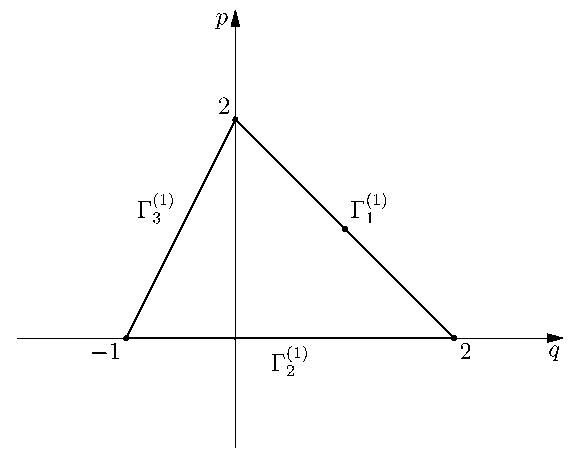
Рис. 2. Проекция многогранника Ньютона гамильтониана (7) пространственной задачи Хилла

Ребро Г^ ) содержит вершины (2,0) , (0,2) и точку (1,1) . Его вектор нормали N" = (1,1) G К ^ . Ему соответствует укороченная функция Гамильтона

HHenon = H11) = 2 (y2 + y2 + уз) + x2y1 - x1 y2 - 2 (2x1 - x2 - x2) , которая описывает промежуточную задачу Энона. Эта задача занимает промежуточное место между задачей двух тел и задачей Хилла. Степенное преобразование хг = ^C|Хг, уг = ^C|¥г, C » 0, i = 1, 2, 3, приводит гамильтониан (7) к виду

H_H iii( X , Y ) = H_Henon( X , Y )-- , ^E =,

Hilly ,         Henony ,         X^ + X2 + X2 , где £ = |C|-3/2. Следовательно, при больших значениях |C| задачу Хилла можно рассматривать как возмущение интегрируемой промежуточной задачи Энона. Такой прием в случае плоской задачи Хилла был использован Л. Перко (L. Perko) для доказательства существования семейств симметричных периодических решений задачи Хилла (см. [13; 14]).

Ребро Г ^¹) содержит вершины ( — 1,0) и (2,0) . Его вектор нормали N 2 ’ = (0,1) лежит вне конусов задачи К ‘ 1₂ , поэтому соответствующее укорочение гамильтониана (7) не рассматривается.

Ребро Г 3¹) содержит вершины ( - 1, 0) и (0, 2) . Его вектор нормали N 33 = ( - 2,1) G К 1 ‘ . Ему соответствует укороченная функция Гамильтона

H Kepler = Н^¹ = Z ( y ² + y ² + ^у з )    / 2 । 2 Г ^,

• ²                yx 1 + x 2 + x 3

которая описывает задачу двух тел (задачу Кеплера) в неподвижной системе координат. Степенное преобразование

Xi = eXi, yi = ' /Х^. t = e-3/2s, e < 1, i = 1, 2, 3, приводит гамильтониан (7) к виду

ε ³

H Hill ^{( X} , ^{Y )} = ^H Kepler ( X , ^{Y )} + ^{e 3/2} (X 2 Y 1 ^— X 1 Y 2 ) 2" ( ^2X 1 ^{— X} 2 ^{— X} 3 ) •

Следовательно, при малых ε задачу Хилла можно рассматривать как возмущение интегрируемой задачи двух тел.

Укорочения, соответствующие вершинам Г ⁽⁰⁾ , не рассматриваются в силу тех же причин, что указаны в п. 1.

Заключение

Методами степенной геометрии [4] были получены четыре предельных случая пространственной ограниченной задачи трех тел и два предельных случая пространственной задачи Хилла. Показано, как с помощью степенных преобразований представить неин-тегрируемую задачу в виде возмущения интегрируемой.