Гармонические функции на конусах модельных многообразий

Данная работа посвящена исследованию поведения решений уравнения Лапласа — Бельтрами на конусах модельных многообразий.

В исследованиях последних десятилетий была отмечена глубокая связь между классическими проблемами теории функций, теорией уравнений в частных производных эллиптического типа второго порядка, в частности уравнения Лапласа — Бельтрами и стационарного уравнения Шредингера, и геометрией римановых многообразий.

В качестве модельного примера для построения общей теории и выявления ее главных направлений, как правило, используется теория гармонических (субгармонических) функций в евклидовом пространстве R ” .

С общей точки зрения представляет особый интерес выявление такого класса некомпактных римановых многообразий, который, с одной стороны, включал бы в себя евклидово пространство, гиперболическое пространство и все пространства со сферичес-ки-симметричной метрикой (далее — модельные многообразия), а с другой стороны, для которого существовала бы возможность построения достаточно полной и законченной теории указанных ранее операторов и их обобщений.

В настоящей работе вводится класс римановых многообразий с непустым краем, и на основе спектральных свойств таких многообразий получена достаточно полная качественная теория решений уравнения Лапласа — Бельтрами.

Истоки указанной проблематики восходят к классификационной теории двумерных некомпактных римановых многообразий и поверхностей, основанной на изучении некоторых функциональных классов на поверхностях. Из теоремы об униформизации следует, что всякая односвязная риманова поверхность конформно эквивалентна одной из следующих модельных поверхностей:

• 1.    Сфере (поверхность эллиптического типа).

• 2.    Комплексной плоскости (поверхность параболического типа).

• 3.    Единичному диску, или, что то же самое, гиперболической плоскости с ее комплексно аналитической структурой (поверхность гиперболического типа).

Определение эллиптичности типа достаточно просто и заключается в определении компактности поверхности. Значительно больший интерес вызывает задача определения параболического и гиперболического типов. Отличительным свойством двумерных поверхностей параболического (гиперболического) типа является выполнение (невыполнение) для них теоремы Лиувилля, утверждающей, что всякая положительная супергармоническая функция на данной поверхности является тождественной постоянной. Данное свойство служит основой для распространения понятий параболичности и гиперболичности на римановы многообразия размерности выше двух. А именно, многообразия, на которых всякая ограниченная снизу супергармоническая функция равна константе, называют многообразиями параболического типа.

К числу одного из первых эффектных геометрических результатов в определении типа риманова многообразия относится теорема С.Я. Ченга и С.Т. Яу [11], утверждающая, что полное многообразие является параболическим, если объем геодезического шара радиуса R растет не быстрее, чем R² при R ^ то . Однако существуют многообразия параболического типа с произвольным ростом объема геодезического шара.

В работе [1] А.А. Григорьян доказал, что параболичность типа полного риманова многообразия М эквивалентна тому, что вариационная емкость любого компакта в М равна нулю.

Вообще, поиски признаков параболичности типа имеют большую историю. Общее представление о современных исследованиях в данном вопросе можно получить из обзоров А.А. Григорьяна [12], В.М. Миклюкова [9], С.Т. Яу [17].

Вопросы существования нетривиальных гармонических и супергармонических функций естественным образом приводят к теоремам типа Лиувилля. Классическая формулировка теоремы Лиувилля утверждает, что всякая ограниченная гармоническая в R ” функция является тождественной постоянной. Хорошо известна справедливость следующих утверждений, носящих название теорем типа Лиувилля.

• 1.    Если гармоническая функция и в R ⁿ имеет конечный интеграл Дирихле, то и = const.

• 2.    Если и Е L ^p ( R ⁿ ) является гармонической функцией и 1 <  р <  то , то и = 0 .

• 3.    Если функция и — гармоническая в R ⁿ и удовлетворяет неравенству | и(ж) | <  С (1 + | ж | ) ^т , то и — гармонический полином степени, не превышающей т .

В последнее время осуществляется следующий подход к теоремам типа Лиувилля. Пусть на римановом многообразии М задан класс функций А и эллиптический оператор L . Будем говорить, что на М выполнено (А, L) -лиувиллево свойство, если любое решение уравнения Lu = 0, принадлежащее функциональному классу А , является тождественной постоянной.

Вместе с тем класс полных многообразий, на которых существуют нетривиальные ограниченные гармонические функции, достаточно обширен. В последнее время наметилась тенденция к более общему подходу к теоремам типа Лиувилля, а именно, оцениваются размерности различных пространств гармонических функций (см., например: [2–5; 7; 14; 15]).

Достаточно серьезный интерес вызывают вопросы разрешимости задачи Дирихле. Вообще говоря, на произвольном некомпактном римановом многообразии поставить задачу Дирихле о восстановлении гармонической функции по граничным данным на «бесконечности» достаточно затруднительно. Однако в некоторых случаях геометрическая компактификация многообразия позволяет сделать это. Например, в [10] и [16] показано, что для односвязного pиманового многообpазия отpицательной секционной кpивизны sect M, удовлетвоpяющей условиям

• —Ь ² <  sect M < — а ² < 0,

существует геометpическа я компактификация, добавляющая сфеpу на бесконечности S ( то ) , и доказано, что на М = М U S ( to ) разрешима задача Дирихле для непрерывных граничных данных на S ( то ) .

Работы ряда математиков были посвящены изучению сферически-симметричных многообразий, которые также называют модельными многообразиями. Опишем данные многообразия подробнее.

Фиксируем начало координат О Е R ⁿ и некоторую гладкую функцию д на интервале [0, R 0 ) ( R 0 может быть то ) такую, что д(0) = 0 и д' (0) = 1 . Определим модельное риманово многообразие М _д следующим образом:

• 1)    множество точек М _д является открытым шаром в R ⁿ радиуса R 0 с центром в О (если R 0 = то , то все R ⁿ );

• 2)    в полярных координатах (г, 6) (где г Е (0, R ₀ ) и 6 Е S ^п- 1 ) риманова метрика на М _д \ { О } определяется как

ds² = dr ² + д ² (г)^6 ² ,                                   (1)

где d6 — стандартная риманова метрика на сфере S ^п- 1 ;

• 3)    риманова метрика в О является гладким продолжением (1).

Примерами таких многообразий могут служить евклидово пространство R ⁿ , гиперболическое пространство H ⁿ , поверхности вращения и т. д.

Замечание 1. Отметим, что многообразие Мд является параболическим тогда и только тогда, когда

∞

Т О

д^{1 n} (t)dt =

то .

Введем обозначение

J = /~g1-n(^) Ц'gn-3(()d() J то            \J то            / dt,

где r ₀ = const > 0, n = dim М .

Замечание 2. В работах [7; 8], в частности, доказаны следующие результаты:

• 1.    Если J = то , то всякая положительная гармоническая на М _д функция является тождественной постоянной.

• 2.    Если J <  то , то для любой ^(6) G С(S ⁿ 1 ) существует единственная гармоническая на М _д функция, такая что lim u(r, 6) = ^(6) .

т ^^

Далее будем говорить, что М — конус модельного многообразия, если М = В UD, где В — некоторый предкомпакт с непустой внутренностью, а D изометрично прямому произведению [r0, +то) х Q (где r0 > 0, Q — компактное риманово многообразие с непустым гладким краем) с метрикой ds2 = dr2 + g2(r)d62.

Здесь g(r) — положительная гладкая на [r ₀ , + то ) функция, а d6 — метрика на Q . Отметим, что в случае Q — компактное риманово многообразие с пустым краем (или, в частности, Q = S ^n-1 , как выше), получаем определение модельного многообразия.

М

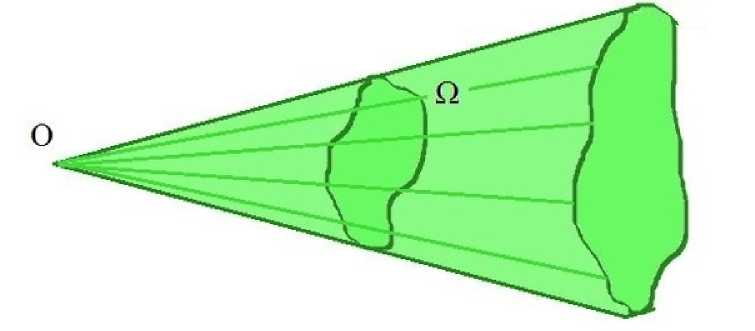
Конус модельного многообразия

Обозначим через Н 0 (М ) пространство гармонических на М функций, для которых выполнено нулевое условие Дирихле на дМ , то есть

Н о (М) = {и : Au = 0,u | _dM = 0 } .

Теорема 1. Пусть многообразие М такое, что J = то . Тогда всякая ограниченная функция u G Н 0 (М ) является тождественным нулем.

Доказательство. Покажем вначале, что для любой ограниченной функции и Е Н ₀ (М ) выполнено lim и(г, в) = 0 .

Т ^^

Заметим, что в координатах (г, в) оператор Лапласа — Бельтрами на D имеет вид (см., например: [7])

д ²              д ’ (г) д 1

дг ^{2     П} д(г) дг   д²(г) ⁶¹

где А ₆ — внутренний лапласиан на Q .

Пусть { w _k (в) } — ортонормированный базис в L²(^) из собственных функций оператора Лапласа А ₆ с нулевым условием Дирихле на д Q , а A _k — соответствующие собственные числа ( 0 < А ₁ < А ₂ <  А ₃ <  ...) . Тогда для любого г справедливо разложение

∞

и(г,в) = ^ V k (r)w _k (в), k =1

где

V k (г) = j и(г,в)^(в)dв.                               (3)

Q

Из (2) следует, что для любого номера к функция v _k (г) является решением следующего обыкновенного дифференциального уравнения:

у " ( г ) + (п - 1) ^д-^(г) у ‘ (г) - -^у(г) = 0,                      (4)

д(г)           д ² (г)

где А = А к .

Замечание 3. Асимптотическое поведение решений уравнения (4) достаточно подробно изучено в [7]. В частности, там доказана справедливость следующих положений:

• 1.    Если J <  то , то для любых констант а и b существует решение уравнения (4), удовлетворяющее условиям у(г ₀ ) = а и lim у(г) = b .

• 2.    Если J = то , то любое ограниченное решение уравнения (4) удовлетворяет условию lim v _k (г) = 0, причем | v _k (г) | — монотонно убывает.

• 3.    Если J = то , A _k < A _k+1 и v _{k +1} ^ + то при г > то , то lim '“^i^ = то .

Т ^^

Т ^^

Т ^^ ^^{к (Т)}

Из ограниченности и(г, в) и (3) следует ограниченность v _k (г) для любого номера к . Тогда, учитывая п. 2 замечания 3, получаем, что lim v _k (г) = 0 для всех к . В [1]

Т^^ показано, что для любой константы р справедливо неравенство к (го)| < А|,                                       (5)

где с ₁ — константа, зависящая от Q и р . В [13] показано, что

\W k (в) | <  С 2 А ^(и-2)/2 ,

где с ₂ — константа, зависящая от Q . Учитывая монотонное убывание lV _k (г) | (см. п. 2 замечания 3), а также неравенства (5) и (6), получаем справедливость неравенств:

∞∞

VVk(r)Wk(6) < V \Vk(r)||Wfc(6)| < k=1k

∞∞

• < V Ivk(rc)||wk(6)| < сз V A'--p.

k=1

Учитывая асимптотику Вейля

С ^- 1 (П)к 2 - 1 <  A k <  С^к 2 - 1 , получаем, что при достаточно больших р ряд, стоящий в правой части (7), сходится. Тогда из признака Вейерштрасса получаем равномерную сходимость ряда

∞

52 V k (r)w k (6).

k=1

Далее, из того, что lim v _k (г) = 0, получаем

Т ^^

∞ lim и(г,6) = lim 5 Vk(r)wk(6) = 0.

Т ^^         Т ^^ ^—^

k =1

Применяя признак максимума, приходим к выводу, что функция и = 0 . Теорема доказана.

Теорема 2. Пусть многообразие М такое, что J = ж. Тогда размерность конуса положительных гармонических функций из класса Н 0 (М ) равна единице.

Доказательство. Пусть и — положительная гармоническая на М функция из Н 0 (М ) . Тогда на D для любого г G [г ₀ , + ж ) справедливо разложение

∞

и(г,6) = ^ Vk(r)wk(6), k=1

где v _k (г) представимо в виде (3) и удовлетворяет уравнению (4). Учитывая положительность w 1 (6) и знакопеременность w _k (6) при к >  2 , запишем:

∞

и(г, 6) = v i (r)w i (6) + 52 V k (r)w k (6).

k=2

Из положительности функции и(г, 6) , линейной независимости {w _k (6) } , учитывая п. 3 замечания 3, получаем, что при к >  2

lim v _k (г) = 0.

Т ^^

Более того, точно так же, как в предыдущей теореме, несложно показать, что

∞ lim V Vk(r)wk(6) = 0.

Т^^ ' -*

k =2

Тогда из [6] следует, что любая положительная гармоническая на М функция представима в виде и = Av 1 (r)w 1 (0) , где А — некоторая константа. Теорема доказана.

Замечание 4. В работе [3] доказано, что если J < то, то для любых р(0) Е С(Q), / G Е С(дМ), таких что lim sup |/(г, 0) — р(^)| = 0, существует единственная гармониче-т^^ Q ская функция и, такая что и(г, 9)\ам = / (г, 0)|ам, lim sup |и(г, 0) — р(0)| = 0, то есть r^“ Q однозначно разрешима задача Дирихле.