Газодинамические неустойчивости в неравновесной химически активной среде

DOI:

Газодинамические неустойчивости играют определяющую роль при формировании волновых структур в различных физических системах [9; 10; 18; 21; 33; 35; 39–41] и астрофизических объектах [15; 23; 24; 30]. При исследовании устойчивости газодинамических течений важным этапом является проведение линейного анализа устойчивости и вывод дисперсионных уравнений, на основе которых изучается динамика малых возмущений в различных средах (однородных и неоднородных) и определяются параметры течения, допускающие возникновение неустойчивых решений [1; 9; 22; 25; 26; 32; 33; 35]. Результаты линейного анализа устойчивости позволяют создавать начальные конфигурации параметров течения для задач численного нелинейного моделирования с контролируемыми (заданными) свойствами устойчивости [9; 15; 18; 23; 24; 30; 33].

В обычных равновесных диссипативных средах звуковые волны затухают и не приводят к образованию каких-либо наблюдаемых волновых структур. При определенных условиях вязкость среды может приводить к появлению диссипативной неустойчивости акустических возмущений на фронте плоских ударных волн произвольной интенсивности [17]. Особая модель турбулентной вязкости [36; 37] наряду с дифференциальностью вращения газовых астрофизических дисков (околозвездные и аккреционные) также приводит к диссипативной акустической неустойчивости [25; 26; 36; 38], которая на нелинейной стадии развития эволюционирует к системе ударных волн, увеличивающих темп аккреции (падение вещества) на компактные релятивистские объекты (белые карлики, нейтронные звезды и черные дыры) [15]. В аккреционных дисках может также возникать и тепловая неустойчивость из-за дисбаланса между диссипативным тепловыделением и высвечиванием энергии излучением, который обусловлен различной зависимостью функций нагрева и охлаждения от плотности и температуры газа [26; 36].

Важным типом неустойчивости, возникающей во многих физических системах при сдвиговых течениях жидкости, газа и плазмы, является неустойчивость тангенциального разрыва скорости или неустойчивость Кельвина — Гельмгольца [8]. Для струйных течений характерно наличие двух тангенциальных разрывов скорости на границах струи, которые при сверхзвуковом режиме течения наряду с поверхностными модами Кельвина — Гельмгольца приводят к возникновение неустойчивых отражательных (симметричных и антисимметричных) гармоник струи, обусловленных эффектом сверхотражения волн от границ струи. [22; 23; 30; 32]. Симметричные или пинч-моды струи приводят к формированию на нелинейной стадии развития неустойчивости дисков Маха [30], а антисимметричные или изгибные моды искривляют форму струи [23].

В неравновесных средах релаксационные и химические процессы в колебательновозбужденном газе могут при определенных условиях приводить к возникновению акустической неустойчивости, которая обусловлена появлением положительной обратной связи между газодинамическим возмущением и неравновесным тепловыделением из-за отрицательных значений второй объемной вязкости [1–3; 9; 11–13; 20; 28; 29; 31; 33; 35]. Кроме того, в таких неравновесных средах при высокой интенсивности нагрева газа может возникать и тепловая неустойчивость энтропийных мод.

Целью работы является изучение влияние релаксационных и химических процессов на устойчивость неравновесного колебательно-возбужденного газа в однородных и неоднородных средах. В разделе 1 описана математическая модель неравновесного газа с учетом колебательной релаксации, химических реакций, вязкости, теплопроводности, нагрева и охлаждения. Влияние химической активности газа на линейную динамику акустической и тепловой неустойчивостей рассмотрено в разделе 2. В разделе 3 для неравновесного колебательно-возбужденного газа построена математическая модель линейной динамики неустойчивостей тангенциального разрыва скорости и раздела двух сред с различной степенью неравновесности.

1.    Математическая модель неравновесного химически активного газа

Рассмотрим простейшую модель неравновесного колебательно-возбужденного газа [7; 9; 33] с учетом химических реакций [12], вязкости и теплопроводности [1; 18]. В двухтемпературном приближении неравновесный химически активный газ характеризуется следующими величинами: скоростью течения ( u = {и _х ,и _у ,u _z }), плотностью (р), давлением (р), термодинамической температурой (Т ), удельной колебательной энергией (е ^ ) или колебательной температурой (Т ), массовой долей химически активного реагента (У) и массовой долей продукта реакции (Z ). Тогда с учетом уравнения состояния идеального газа (р = RqT , где R = R * /M — газовая постоянная, R * — универсальная газовая постоянная, ℳ — молярная масса газа) система газодинамических уравнений

примет вид:	= - q V- u ,                               (1) dt d u    Vp  V е ,, =       +      ,                                      (2) dt       Q     Q
1 d Y - 1 dt	( p ) =    - d? + Q -л + (^ + 1V. U ( p \\,   (3) \q) Q dt    dt                  q       Rq     [ Qq J _ ^ = _     ' +Q,                       (4) dt         т dy — = -К + q,   Z = 1 -У,                  (5) dt

d где It

д

=   + u • V; V = dt

( д d £1 t дх’ ду’ dz J

; ст — тензор вязких напряжений [8]; y — по казатель адиабаты; ди — коэффициент теплопроводности; eV — удельная колебательная энергия газа в невозбужденном (равновесном) состоянии; τ — время колебательной ре-

лаксации; Q и Л — удельные мощности нагрева (накачки) и охлаждения (теплоотвода);

К и q — удельные скорости химической реакции и притока реагента У соответственно. Величины т, Q и Л могут зависеть от плотности и температуры. Газ нагревается как внешним источником накачки Q^, так и за счет выделения энергии в химической реакции Q(a):

Q = Q ^{( s}} + Q ^{( a )} .                                     (6)

Удельная мощность нагрева Q ^{( a )} связана с К соотношением: Q ^{( a )} = НК , где Н — энтальпия химической реакции. В общем случае удельная скорость химической реакции является функцией плотности, температуры и массовой доли химически активного реагента: К ( q,T,Y ). Например, для простейших химических реакций первого порядка имеем: К ( q,T,Y ) = K 0 Y exp {—T _a /T }, где К 0 — константа скорости реакции, Т _а — температура активации.

Удельная колебательная энергия газа e _V связана с его колебательной температурой T _v следующим соотношением [6; 18; 19]:

^ ^rj^ ^e V ^{( t} V )     ^    . /Л /ГТ \ -I ,

V exp(Q _e /T _v ) - 1

где 0 ^ — характеристическая колебательная температура 1-моды, а г ^ — степень вырождения 1-моды. В равновесное значение удельной колебательной энергии получается из (7) при T _v = Т , то есть e V = e _V (Т ).

Время колебательной релаксации газа в общем случае можно представить в виде [4; 6; 18]:

т ^п exp(a o + a i T ^{1 / 3} + а 2 Т ^{2 / 3} + а з Т ^{1 / 3} ) ^т( Р,^т ) = —

P

1-

m exp(-0 min /T )

,

где р> = р/р _А , P a — атмосферное давление, 0 _min — минимальная из характеристических температур колебательных мод [4], коэффициенты а ₀ , а 1 , а ₂ , а ₃ и п вычисляются на основе полуэмпирических формул [4; 5; 34] или определяются экспериментально [6; 14]. В (8) входит также бинарный параметр m = (0,1), который позволяет учитывать поправку кинетической теории [4].

2.    Акустическая и тепловая неустойчивости в неравновесном химически активном газе

Рассмотрим случай однородной и покоящейся стационарной среды в одномерном приближении. В рамках линейного анализа устойчивости решение системы уравнений (1)-(5) ищется в виде f = f0 + f(t, x), где f0 = const — начальные стационарные значения параметров течения, а f(t,x) — функция малых возмущений (|f| ^ |f0|). Подставляя эти решения в исходную систему нелинейных дифференциальных уравнений и учитывая только линейные по возмущениям f слагаемые получим линеаризованную систему дифференциальных уравнений, описывающих динамику малых линейных возмущений в химически активном неравновесном газе. Для однородной среды все возмущенные величины можно представить в виде плоских гармонических волн (ВКБ-приближение): f (t,x) = f(w, к) exp {-i^t + ikx} с частотой ш и волновым числом к. Подставляя ВКБ-решение в систему линеаризованных дифференциальных уравнений получим систему линейных алгебраических уравнений (СЛАУ) относительно их комплексных амплитуд f, разрешая которую (приравнивая определитель этой системы к нулю) получим стандартное дисперсионное уравнение 4-го порядка [1], модифициро- ванное с учетом химических реакций, которое описывает звуковые и энтропийные моды колебаний:

Y [ш (YU + 1) + /

-

⁺ { ^ш [ ^A 2 ^{+ р} 0 ^B 1 ^{— ш 2 (}Х 0 ⁺ М 0 ) ] ⁺ ^ [ ^B 2

ш ² y Ц0)] к ⁴ +

>^— си ^{2 (1 + х} 0 ^{+ А} 1 Ц 0 ) ]} ^{р 2 —}

— ш ² [ шА 1 + / ( B 1 — ш ² )] — 0 ,

где ш — шт ₀ ; к — кс , т ₀ ; х ₀ — Х 0 с 2 т ₀ ; х ₀ — Y i®₀ /^£ ₀ — коэффициент температуропроводности; с , — у/YP 0 / Q ₀ — высокочастотная (замороженная) скорость звука; Y i — Y — 1;

(4         А р0 — р.0с2т0, р0 — I - ц01 + цо2 ; ц01 и р.02 — коэффициенты первой и второй кинемати-

Yi ческой вязкости; Ai — 1+ Yi[C0 + ^0(тт + Лт)]; ^2 — 1+--[Су + ^0(тт — т, + Лт

-

Л , )];

^B i — ^Y i 8 о ^(Л т

-

Qt ); B ₂ — ^(Q

γ пень неравновесности среды; Cv —

, ^{— Q} t ^{— Л} , ^{+ Л} т ^); 5 q ^{—      —} безразмерная сте^-

Л^ 0

^    — безразмерный коэффициент удельной

Я\^дТ /0

колебательной теплоемкости; безразмерные параметры вида f, и fT, где f — (т, Q, Л), (9lnfА        (5lnf А определяются следующими образом: fe — I дЩ^ ’   — I дln!  ’

В работе [1] подробно описана процедура вывода дисперсионного уравнения (9) для неравновесного колебательно-возбужденного газа с учетом вязкости, теплопроводности, произвольных зависимостей времени релаксации, нагрева и охлаждения от термодинамических параметров среды (плотности и температуры). При учете химических реакций (5) и выражения (6) общий вид дисперсионного уравнения (9) не изменяется, а переопределяются только параметры Q _e и Q_t :

Q _e — (1 — e)Q ,^{s )} + eQ , ^a)

•( а )

/шт, 1

• — (а) /шт,

-

,

Qt — (1 — e)Q T + eQ ^

•( ^а )

/шт, 1

•--(а)

/шт ,

-

,

где в — Q^ /Q o — доля химического энерговыделения в общей мощности нагрева; т , ^{а )} — т , ^{а )} /т ₀ , т , ^{а )} — Y ₀ H/ Q^Qy^ — характерное время химической реакции; _П( а,, ) _ (д lnQ^ \ ( а,. ) _ / д l .Q \ ( а ) _ (д ln - - \

^{Q —} д ln в J;^{Qt —} д ln? J_o’^{Qy —} д lnY

Дисперсионное уравнение (9) является биквадратным относительно волнового числа (Ь ₄ к ⁴ + Ь ₂ к ² + Ь ₀ — 0) с коэффициентами b j , зависящими от частоты ш и безразмерных параметров модели ( y , С ,5 о , т 0 ^{а )} ,р 0 ,Х 0 , т , , т т , Q^, Qt^ , Q^, Л _в , Л т ). Поэтому здесь будем рассматривать случай пространственного анализа устойчивости, в котором закон

дисперсии представляется в виде функции к(ш) с комплексным к и вещественным ш, а уравнение (9) имеет простое аналитическое решение:

Y      / ^{— Ь}2 ± ^ ^b 2 ^{— 4 b} 4 ^b 0

к — ±v-------2b4-------’ где комплексное волновое число можно представить в виде к = кг + iki. Инкремент неустойчивости определим как а = -к > 0, а фазовую скорость волны — с = со/кг. Решение (12) описывает две пары мод (звуковую и энтропийную), распространяющихся в противоположных направлениях от источника возмущений. Для выделения нужной моды достаточно сравнить фазовые скорости волн, фазовая скорость звука всегда по модулю больше фазовой скорости энтропийных волн. Если пренебречь теплопроводностью (хо = 0), то дисперсионное уравнение (9) вырождается (становится квадратным) и его решение описывает только акустические волны: к = ±у/-Ь0/Ь2.

В качестве базовых значений безразмерных параметров модели выберем [16; 18]: Y = 1,4, С; = 0,0888, S o = 0,5, т ' = 1, й о = Х о = 10 ^-4 , т _е = -1, т _т = -4,3333, СХ° = 0, Q T = 0, Q T = 10, Q ? = 1, Л , = 0, Л _т = 1,4286.

Влияние химических реакций в неравновесном колебательно-возбужденном газе на закон дисперсии неустойчивых звуковых волн показано на рисунках 1–2. Видно, что химическая активность среды оказывает достаточно сильное влияние на динамику акустической неустойчивости только в диапазоне частот 0,1 < со < 10. Зависимости как акустического инкремента, так и фазовой скорости звука от параметров в и т 0 ^Т ) в этой области частот имеют немонотонный характер. Кроме того, в диапазоне частот 0, 2 < О < 0, 6 при значениях параметра в ~ 0, 25-0,5 фазовая скорость звука оказывается аномально высокой. Так при в = 0, 5 точке со ~ 0, 36 на дисперсионных кривых появляется разрыв второго рода, где фазовая скорость звука и акустический инкремент обращаются в ∞. Ранее этот эффект был обнаружен в работе [1] при рассмотрении неравновесного колебательно-возбужденного газа без учета химических реакций, но для случая более высоких значений степени неравновесности среды S _o > 1. Отметим, что область с аномальными значениями а и с попадает в зону запрещенных частот, в которой звуковые волны распространяться не могут из-за отрицательных значений плотности волновой энергии и энергетической скорости волны [27].

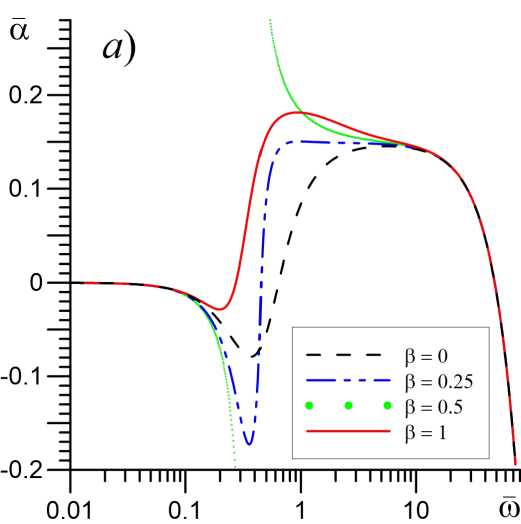
Рис. 1. Закон дисперсии звуковых волн для случая S 0 = 0, 5. Показаны зависимости акустического инкремента а (а) и фазовой скорости звука с (b) от частоты со при различных

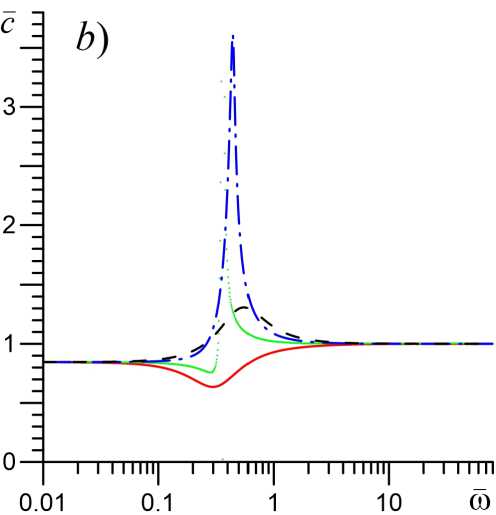
значениях доли химического энерговыделения β

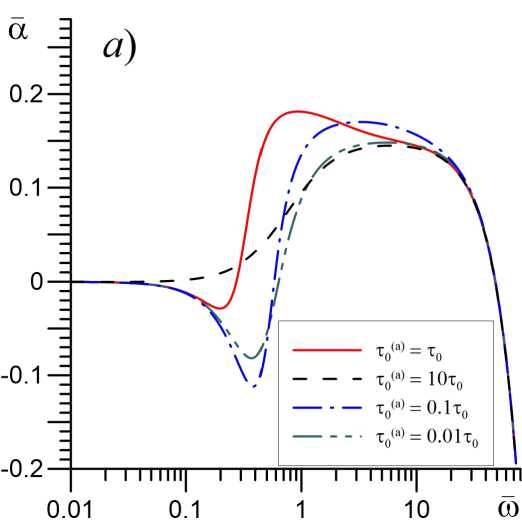
Рис. 2. Закон дисперсии звуковых волн для случая S ₀ = 0, 5 и в = 1. Показаны зависимости акустического инкремента a (a) и фазовой скорости звука с (b) от частоты си при различных (а) значениях характерного времени химической реакции т 0

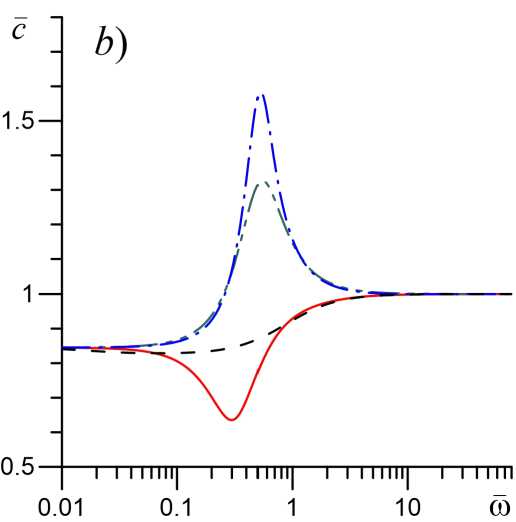
На рисунке 3 показана зависимость инкремента тепловой неустойчивости при различных значениях доли химического энерговыделения β и характерного времени химической реакции f jf) . Характерной особенностью тепловой неустойчивости является ее низкочастотный характер си < 1, высокие значения инкремента, превышающие акустический инкремент на несколько порядков, а также малые значения фазовой скорости энтропийных волн, которые, наоборот, на несколько порядков меньше скорости звука. Видно, что влияние параметров химической реакции на закон дисперсии энтропийных волн также имеет немонотонный характер. Кроме того, учет химической активности среды приводит к снижению критического значения степени неравновесности среды, после которого возможно развитие тепловой неустойчивости. Ранее в работе [1] было показано, что тепловая неустойчивость возникает при больших значениях S o >  2.

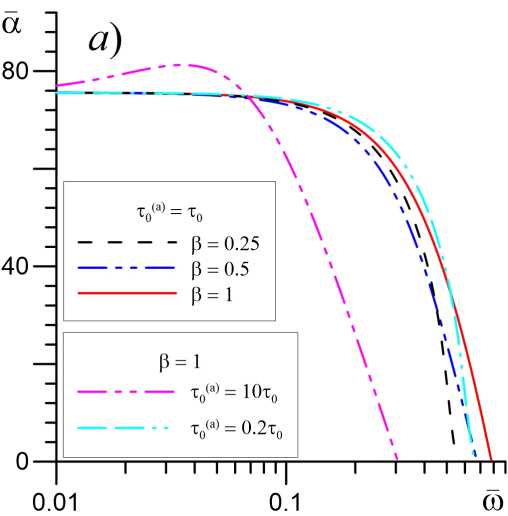
Рис. 3. Закон дисперсии энтропийных волн для случая S ₀ = 1. Показана зависимость

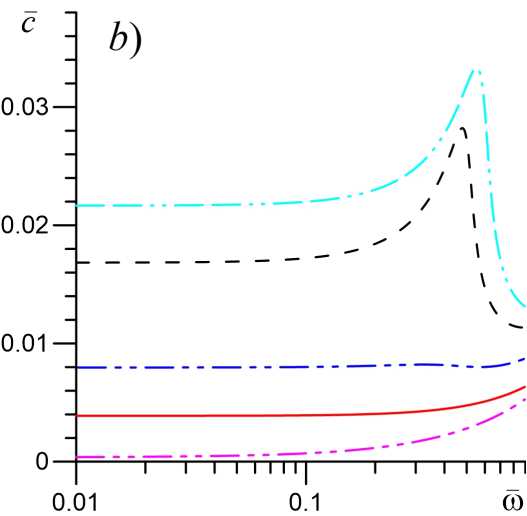
инкремента тепловой неустойчивости а и фазовой скорости с (b) от частоты со при различных значениях параметров в и т^а)

3.    Линейный анализ устойчивости неоднородных по г-координате неравновесных химически активных сред

Рассмотрим случай, когда начальные стационарные распределения параметров течения в среде зависят от г-координаты и газ движется вдоль х со скоростью u _o ( z ) . Применим стандартную процедуру линеаризации системы уравнений (1)–(5), то есть будем искать решение в виде: f (1,х,у,г) = f ₀ (г) + f (кх,у,у,г ), где для возмущенных величин используем выражение f (Ь,х,у,г ) = f(г)exp{—гwt + ik _x x + ik _y у}, k _x и к _у — волновые числа вдоль х и у координат, соответственно. Учитывая только линейные по возмущениям слагаемые и проводя несложные выкладки получим следующую систему линеаризованных уравнений, описывающих динамику малых возмущений (|f | ^ |f ₀ |) в неоднородной химически активной среде:

—iwQ + Q _o u _z = — q _o (ik _x u _x + ik _y u _y + u ‘_z ),                    (13)

̃︀

′

• — i^U x + ^ o ^ z

• —    ik x ^, Q o

• — iw u _y = —ik_y — , Q o

′

• — iwU z = — - , Q o

Dp = c 2 Q,

где w = w — k _x u ₀ — доплеровская частота; f ‘ = df /дг; D =

A i wT o + i(B i — w ² T 2 ) А 2 Й T o + i(B 2 — w ² T 2 ).

Все коэффициенты и параметры модели определяются в соответствии с разделом 2.

̃︀

Исключая из системы (13)-(17) u _x , u _y , q и вводя г-смещение среды u _z = d^/dt =

̃︀

= —iw £, получим систему обыкновенных дифференциальных уравнений относительно комплексных г-амплитуд возмущенных величин (давления p и г-смещения среды ^):

^ = ( k l _— D \ ) — ⁽ q o dz     w ² C 2 Q o Q o

︀

+

^k x ^u o \ )

^ , ω ︀

dp)

,  = Qo dг

2 г w ^ ,

где k 2 = k x + k y .

На основе системы уравнений (18)–(19) для физически однородных сред можно сформулировать краевую задачу, которая позволяет исследовать устойчивость раздела сред с различными значениями параметров течения. Задача включает граничные условия при г ^ ±то и условия сшивки возмущенных величин p и | на границе раздела сред. В рамках данного подхода рассмотрен временной анализ устойчивости, в котором закон дисперсии определяется функцией w(k) с комплексной частотой w и вещественное волновым числом k.

3.1.    Неустойчивость тангенциального разрыва скорости

Исследуем влияние релаксационных и химических процессов в неравновесных средах на классическую неустойчивость Кельвина — Гельмгольца, которая возникает на границе раздела сред с тангенциальным разрывом скорости [8]. Рассмотрим две физически однородные среды с границей раздела при z = 0, движущиеся в противоположных направлениях по х-координате со скоростями и ± = ±и ₀ . Система уравнений (18)-(19) для этих сред примет вид:

Zk ± _ ( ^k l    ^D ± \ Р ± Zp± _    - 2 7

Zz    \(3 ±     с 2 J д ₀ ’ Zz @ 0 ± ±

̂︀

̂︀

Условия сшивки решений (20) при z = 0: ^ + (0) = ^ - (0) и р + (0) = р — (0). Решения системы (20), удовлетворяющие граничным условиям lim |/1 = 0 имеют вид: |г|чм

̂︀

Wz) = а ± exp(^A ± z),

ω ̂︀ ²

p ± (z ) = Т@о . а ± exp(^A _± z). λ ±

Подставляя решения (21) в (20) и решая полученное характеристическое уравнение находим Л ± = к ! — D ± w ± /с 2 (Яе(Х ± ) > 0). Из сшивки смещений получаем а + = а - , а сшивка давлений дает искомое дисперсионное уравнение, записанное в безразмерном виде:

U - Л ₊ + U + Х — = 0 ,                            (22)

^М              2 ^и о             ^к _х        ^А 1 ^и ± + г ⁽ В 1 ^— си ± )

где и ± = и ± — к ± cos 0, М =---, 0 = arccos -—, D ± =---------------5—.

• ²                 ' •              ^к .          А 2 и ± + i(B 2 — и ± )

Релаксационные и химические процессы в неравновесном колебательно-возбужденном газе учитываются в дисперсионном уравнении (22) посредством коэффициентов D ± , которые в общем случае оказываются комплексными и могут оказывать существенное влияние на инкремент неустойчивости Кельвина — Гельмгольца. В пределе слабой нерав-новесности среды (S 0 ^ 1) и В 1 , 2 = 0 дисперсионное уравнение (22) имеет следующее асимптотическое решение для длинноволновых возмущений к ± ^ 1:

ω

к !

-δ

,    . М ²    о     /---:----:—:——

1 + (1 — 6) — cos ² 0 — у 1 + (1 — 6)М ² cos ² 0

где величина 6 (|6| ^ 1) определяет вклад неравновесности в закон дисперсии поверхностных мод Кельвина — Гельмгольца. При 6 = 0 получаем хорошо известное решение для инкремента неустойчивости Кельвина — Гельмгольца [8]. Из (23) следует, что при положительных значениях δ учет неравновесности приводит к дополнительному усилению неустойчивости Кельвина — Гельмгольца на всех режимах течения как дозвуковых, так и сверхзвуковых. Для акустически активного колебательно-возбужденного газа [1] имеем: 6 = А2 — A i >  0.

3.2.    Неустойчивости в сверхзвуковых струях

Рассмотрим плоскую физически однородную струю, граничащую с такой же однородной внешней средой и имеющую два тангенциальных разрыва скорости течения при z = ±hj (2hj — толщина струи). В таких струйных течениях может происходит раскачка (усиление) как поверхностных мод (неустойчивость Кельвина — Гельмгольца [8]), так и отражательных гармоник струи, обусловленных эффектом сверхотражения на границе сверхзвукового тангенциального разрыва скорости [22; 23; 30; 32]. Для упрощения выкладок будем считать, что скорость в струе положительна и0, = и0, а во внешней среде и0,т = —и0. Тогда уравнения (18)-(19) для струи и внешней среды примут вид:

d^j,m    ( ^2    Dj,m\ Pj,m      dpj,m7

~ = а2т—^2     ’   ~=91 "j-1,- ■

Сформулируем краевую задачу для системы (24), записав условия сшивки на границе струи при z = h j и граничное условие в плоскости симметрии струи при z = 0 для симметричной (пинч) S -мода и антисимметричной (изгибной) 45-мода:

Р, (h,) = тт(М ,    p, (h,)= Pm(h,) ,

5 : ^p j (0) = 0 ,     45 : p j (0) = 0 .

Решения системы (24) для внешней среды и струи имеют вид:

k m (z) = a m exp[—A m (z — h j )],

p

P m (z) =

—

9 o

ω ²

— am exp[—A m (z ^A m

—

^h j ^)],

^ j ^{( z )} = ^a j ^exp^{[ A} j ^{( z — h} j ^)] + ^b j ^exp^{[ —A} j ^{( z}

—

^h j ^)],

"j pj (z) = ц" {a, exp[A, (z Aj

—

h j )] — bj exp[— a , (z

—

h j )]} ,

где ^{A j} ,m = k ² _± ^{— D} j,m " ^j.m ' 2 .

Сшивая решения (26) с учетом условий (25) получим искомые дисперсионные уравнения для симметричной и антисимметричной мод струи, записанное в безразмерном виде:

5 : " _m A j [ 1 — exp(—2A , h j ) ] + " j^m [ 1 + exp(—2A , h j ) ] = 0 ,

45 : " m A j [ 1 + exp(—2A j h j ) ] + " , A _m [ 1 — exp(—2A , h j ) ] = 0 .

Также как для случая одиночного тангразрыва скорости, релаксационные и химические процессы в неравновесном колебательно-возбужденном газе учитываются в дисперсионных уравнениях (27) посредством коэффициентов D j, _m , которые также оказываются комплексными и могут оказывать существенное влияние на инкремент неустойчивости отражательных гармоник струи (5- и 45-мод). Дисперсионные уравнения (27) имеют аналогичные (23) асимптотические решения при 5 ^ 1 и |A , h j | ^ 1. Следовательно, в акустически активном газе учет неравновесности также приводит к увеличению инкремента неустойчивости симметричных и антисимметричных мод струи на всех режимах течения как дозвуковых, так и сверхзвуковых.

3.3.    Неустойчивость границы раздела между средами с различными значениями степени неравновесности

Исследуем устойчивость раздела двух покоящихся химически активных сред, раз- личающихся величиной степени неравновесности 50. Из (22) при М = 0 получим персионное уравнение, описывающее динамику малых возмущений на границе раздела двух неравновесных сред с различными значениями Sq.

A + w + i(B + - w 2 ) _ A — w + i(B - - w 2 )

A ^ w + i(B + - w ² ) = A ^- w + i(B - - w ² ) '

Полученное уравнение не зависит от волнового числа, что обусловлено используемым приближением, которое не учитывает влияние вязкости и теплопроводности. Для типичных значений параметров неравновесных колебательно-возбужденных химически активных сред мнимая часть частоты оказывается положительной, то есть граница раздела абсолютно неустойчива для всех длин волн. При учете вязкости и теплопроводности коротковолновые возмущения должны стать устойчивыми. Инкремент обнаруженной неустойчивости зависит как от разности степеней неравновесности сред AS = S + - S - , так и от параметров среды, при определенных значениях которых возможна стабилизация неустойчивости раздела. Если пренебречь зависимостью нагрева и охлаждения от плотности и температуры, то есть положить B ± = В ± = 0, то можно получить явное выражение для частоты:

• .  A-A + - A + A ^-      . /      Y 1 C \

W = i -Г+ ---7----7----7+ = i 1 +           .               (29)

^A 1 ^{- A} 1 + ^A 2 ^{- A} 2          ^{1+ Y} 1 ^T T

Видно, что в этом частном случае частота колебаний границы раздела сред оказывается чисто мнимой и определяет апериодическое затухание (Im w < 0) или нарастание (Im w > 0) амплитуды начальных возмущений. Из (29) следует, что граница раздела двух неравновесных сред устойчива при выполнении условия:--- C _v < т _т < 

Y 1                   Y 1

и зависит только от параметров среды — показателя адиабаты, удельной теплоемкости колебательных степеней свободы и модели времени VT-релаксации.

Заключение

Сформулируем основные результаты работы:

• 1)    Проведено обобщение линейной модели динамики акустических и энтропийных мод в неравновесном колебательно-возбужденном газе для химически активных сред. Получено, что при учете химических реакций общий вид дисперсионного и волнового уравнений не изменяются, а переопределяются только параметры Q _e и Q _T в этих уравнениях. Теперь эти параметры зависят от двух новых величин, характеризующих химические реакции в неравновесном газе: характерного времени химической реакции т ⁽ “ ) и доли химического энерговыделения в общей мощности нагрева газа β.

• 2)    Исследовано влияние химических реакций в неравновесном колебательно-возбужденном газе на закон дисперсии неустойчивых звуковых волн. Показано, что

• химическая активность среды оказывает достаточно сильное влияние на динамику акустической неустойчивости только в диапазоне частот 0.1 < wt < 10. Зависимости как акустического инкремента, так и фазовой скорости звука от параметров в и т(“) в этой области частот имеют немонотонный характер. Кроме того, в диапазоне частот 0.2 < wt < 0.6 при значениях параметра в ~ 0.25-0.5

фазовая скорость звука и акустический инкремент оказываются аномально высокими. Ранее этот эффект был обнаружен при рассмотрении неравновесного колебательно-возбужденного газа без учета химических реакций, но для случая более высоких значений степени неравновесности среды S >  1. Область с аномальными значениями фазовой скорости звука и акустического инкремента попадает в зону запрещенных частот, в которой звуковые волны распространяться не могут из-за отрицательных значений плотности волновой энергии и энергетической скорости волны.

• 3)    Исследовано влияние химических реакций в неравновесном колебательно-возбужденном газе на закон дисперсии неустойчивых энтропийных мод. Характерной особенностью тепловой неустойчивости является ее низкочастотный характер шт < 1, высокие значения инкремента, превышающие акустический инкремент на несколько порядков, а также малые значения фазовой скорости энтропийных волн, которые, наоборот, на несколько порядков меньше скорости звука. Показано, что влияние параметров химической реакции на закон дисперсии энтропийных волн также имеет немонотонный характер. Кроме того, учет химической активности среды приводит к снижению критического значения степени неравновесности среды, после которого возможно развитие тепловой неустойчивости. Ранее для неравновесного колебательно-возбужденного газа без учета химических реакций было показано, что тепловая неустойчивость возникает при более высоких значениях S >  2.

• 4)    Проведен линейный анализ устойчивости химически активной неравновесной среды для случая, когда вдоль одной из пространственных координат (например, г) начальные стационарные распределения параметров течения неоднородны. Получена система обыкновенных дифференциальных уравнений относительно возмущенных величин (давления р и лагранжева г-смещения среды ^), которая позволяет исследовать устойчивость раздела сред с различными значениями параметров течения. Для этих уравнений сформулирована краевая задача, включающая граничные условия при г ^ ±то и условия сшивки возмущенных величин р и ^ на границе раздела сред. В рамках данного подхода рассмотрен временной анализ устойчивости, в котором закон дисперсии определяется функцией ш(к), где ш -комплексная частота, к - вещественное волновое число.

• 5)    Исследовано влияние колебательной релаксации и химической активности в неравновесном газе на устойчивость тангенциального разрыва скорости для двух физически однородных сред, различающихся только значением касательной к границе раздела скорости. Получено дисперсионное уравнение, описывающее линейную динамику неустойчивости Кельвина — Гельмгольца в неравновесном химически активном газе. Показано, что учет колебательной релаксации и химической активности в неравновесном газе приводит к существенному усилению неустойчивости Кельвина — Гельмгольца как для дозвуковых, так и для сверхзвуковых течений. Получены дисперсионные уравнения, описывающие линейную динамику неустойчивых симметричных (пинч) и антисимметричных (изгибных) мод в нерав-

• новесных химически активных сверхзвуковых струях, распространяющихся как в

равновесном невозбужденном газе, так и в неравновесной среде. Показано, что учет колебательной релаксации и химической активности в неравновесном газе приводит к существенному усилению неустойчивых мод джетов (струй) как сим

метричных, так и антисимметричных.

• 6)    Проведено исследование устойчивости раздела двух покоящихся химически активных сред, различающихся величиной степени неравновесности S 0 . Из условия сшивки решений на границе раздела таких сред получено дисперсионное уравнение, которое не зависит от волнового числа. Показано, что для типичных значений параметров неравновесных колебательно-возбужденных химически активных сред мнимая часть частоты оказывается положительной, то есть граница раздела неустойчива. В частном случае при учете только зависимости времени колебательной релаксации от плотности и температуры показано, что инкремент неустойчивости не зависит от разности степеней неравновесности сред, а определяется значениями показателя адиабаты, удельной теплоемкости колебательных степеней свободы и зависимости времени релаксации от плотности и температуры. Зависимость мнимой части частоты от этих параметров позволяет определить критерий устойчивости границы раздела неравновесной и равновесной сред.

ПРИМЕЧАНИЕ

• ¹    Исследование выполнено за счет гранта Российского научного фонда (РНФ) № 2321-00401, https://rscf.ru/project/23-21-00401/ .