Генерация медленных магнитозвуковых колебаний в плазмосфере Земли солнечным терминатором

Собственные медленные магнитозвуковые (ММЗ) колебания магнитосферы Земли, в отличие от альфве-новских волн, исследованы на сегодняшний день достаточно мало [Taylor, Walker, 1987; Leonovich et al., 2006; Klimushkin, Mager, 2008]. В магнитосфере Земли ММЗ-колебания распространяются преимущественно вдоль силовых линий геомагнитного поля. Из-за высокой проводимости ионосфера представляет собой почти идеально отражающую границу для рассматриваемых волн. При этом ММЗ-колебания, как и альфве-новские волны, могут образовывать в магнитосфере стоячие волны вдоль магнитных силовых линий.

Имеется довольно большое число работ, посвященных структуре и спектру стоячих альфвеновских волн в дипольно-подобных моделях магнитосферы (см., например, [Radoski, 1967; Cummings et al., 1969; Leonovich, Mazur, 1989; Chen, Cowley, 1989; Lee, Lysak, 1991; Wright, 1992]). В работе [Leonovich et al., 2006] были рассмотрены стоячие ММЗ-волны, возбуждаемые в дипольной магнитосфере монохро-матической быстрой магнитозвуковой (БМЗ) волной, проникающей внутрь магнитосферы из солнечного ветра. Характерная длина волны таких ММЗ-коле-баний в направлении вдоль силовых линий геомаг-нитного поля и длина волны в азимутальном направлении сопоставимы с характерными размерами неоднородности магнитосферной плазмы. Поперек магнитных оболочек они имеют достаточно выраженную резонансную структуру с характерным масштабом, много меньшим размеров неоднородности магнитосферной плазмы. Их амплитуда резко убывает в направлении от экваториальной плоскости магнитосферы к ионосфере, поэтому зарегистрировать такие колебания можно только на высокоорбитальных космических аппаратах.

Сравнительно малое количество работ, посвященных ММЗ-колебаниям, связано, по-видимому, с тем, что они имеют большой декремент затухания [Leonovich, Kozlov, 2009]. В результате собственные ММЗ-колебания быстро затухают и их достаточно сложно наблюдать. Тем не менее при наличии достаточно интенсивного источника, способного генерировать эти волны, они вполне могут наблюдаться в магнитосфере Земли.

Таким источником может быть солнечный терминатор. В работе [Afraimovich et al., 2009a] по наблюдениям на сети приемников GPS над территорией Японии были зарегистрированы колебания полного электронного содержания (ПЭС), связанные с прохождением терминатора по ионосфере Земли в области, сопряженной с областью наблюдения силовыми линиями геомагнитного поля. Анализ наблюдений позволил установить отчетливую связь колебаний ПЭС в области наблюдения с процессами в магнитосопряженной области ионосферы. В связи с этим было сделано предположение, что взаимодействие магнитосопряженных областей ионосферы происходит через распространение МГД-волн – альфвеновских или ММЗ – вдоль силовых линий геомагнитного поля.

Периоды регистрируемых колебаний ПЭС находились в диапазоне 15–30 мин. Характерные периоды основных гармоник стоячих альфвеновских волн на рассматриваемых магнитных оболочках (~10 с) очень далеки от периодов регистрируемых колебаний ПЭС, поэтому генерация колебаний ПЭС альфвеновской волной представляется маловероятной. Периоды основных гармоник стоячих ММЗ-волн (~20 мин) как раз находятся в нужном диапазоне. В работе [Afraimovich et al., 2009b] наблюдаемые колебания ПЭС на основе расчета периодов нескольких первых гармоник ММЗ-колебаний в ВКБ-приближении интерпретировались как колебания одной из первых гармоник стоячих ММЗ-волн.

ММЗ-волны, связанные с прохождением терминатора, должны иметь достаточно большую характерную длину волны в направлении поперек магнитных оболочек (сравнимую с характерным размером магнитосферной неоднородности) и быть сравнительно мелкомасштабными в азимутальном направлении. Настоящая работа посвящена расчету структуры наблюдаемых вблизи ионосферы компонент поля таких азимутально-мелкомасштабных стоячих ММЗ-волн и их спектра в дипольной модели плазмосферы Земли. Расчеты выполнены как аналитически в приближении ВКБ, так и численно. Проведено сравнение результатов аналитических и численных расчетов с данными наблюдений.

Данная работа имеет следующую структуру. Во втором разделе описана модель среды, выведено основное уравнение для расчета структуры и спектра азимутально-мелкомасштабных стоячих ММЗ-волн и получены аналитические выражения для компонент поля колебаний. В третьем разделе в ВКБ-приближении получено аналитическое решение основного уравнения, описывающего структуру поля колебаний вдоль магнитной силовой линии. В четвертом разделе найдено численное решение основного уравнения, построены распределения компонент поля колебаний вдоль магнитной силовой линии и проведено обсуждение полученных результатов. В заключении перечислены основные результаты данной работы.

Модель среды и основные уравнения

Рассмотрим модель плазмосферы с дипольноподобным магнитным полем, представленную на рис. 1. Введем криволинейную ортогональную систему координат (x 1, x2, x3), связанную с силовыми линиями магнитного поля. Координата x3 направлена вдоль силовой линии, x1 - поперек магнитных оболочек, а x2 дополняет систему координат до правосторонней. Квадрат элемента длины в этой системе координат определяется как ds 2 = gi (dx1 )2 + g2 (dx 2 )2 + g3 (dx 3 )2, где gi (i = 1, 2, 3) - компоненты метрического тензора рассматриваемой криволинейной системы координат. Будем считать плазму и магнитное поле однородными

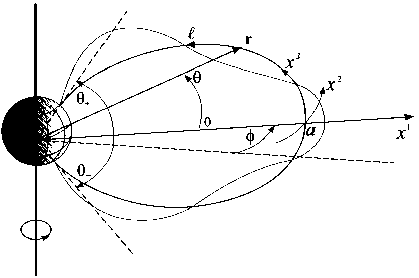
Рис. 1 . Криволинейная ортогональная система координат ( x 1 , x ² , x ³ ), связанная с силовыми линиями магнитного поля, и неортогональная система координат ( a , ф, 0), использованная в численных расчетах. Условно показана структура 5-й гармоники стоячих ММЗ-волн вдоль магнитной силовой линии.

по координате x ². Для описания МГД-колебаний используем систему уравнений идеальной МГД:

dv p— = -VP +--[rot B х B], dt         4n

^ = rot[ v х B ],

^5p + V ( p v ) = 0, 5 t

^Р = 0, dt p^Y

где B и v - векторы напряженности магнитного поля и скорости движения плазмы, р и P - плотность и давление плазмы, у - показатель адиабаты. Для определения напряженности электрического поля колебаний E используем дрейфовое приближение:

E = - [ v х Б ]/ c .

В стационарном состоянии ( 5 / d t = 0) система уравнений (1)-(4) описывает распределение параметров невозмущенной магнитосферы: B ₀, v ₀, E ₀, р₀, P ₀. Будем считать плазму покоящейся ( v ₀= E ₀=0). Линеаризуем систему (1)-(4) относительно малых возмущений, связанных с МГД-колебаниями плазмы: B', v', E', р', P' . Представим каждую из возмущенных компонент в виде разложения Фурье по гармоникам вида exp( ik ₂ x ²- i ю t ), где ю - частота колебаний, k 2 - азимутальное волновое число (если x ² =ф - азимутальный угол, то k ₂= m =1, 2, 3...). Из (1) имеем

- i MP v, = -V, Р'+ B 1  (V B, -V, ^),(5)

^{4 п} gg з

-irop0v2 = -ik^P'-         (ik2B3 - V3B2),(6)

^{4 n} x/ g T

-impo v3 =-V3 P',(7)

где v i , B i ( i =1,2, 3) - ковариантные компоненты векторов возмущенной скорости v ' и магнитного поля B' , V, = 5 / 5 x i . Из (3), (4) получаем

Р = Ч 1 P t: “ v t

х

V ,

^P v , J + ik 2 t gP o ^: v 2 +V 3

( g 1       J       g 2

— ^P 0 ^V 3

I g 3

где g = 4g , g 2 g 3 , ^: = ^1/ Y .

Для описания поля МГД-колебаний удобно перейти к представлению компонент поля колебаний через потенциалы. Согласно теореме разложения Гельмгольца, произвольное векторное поле, в каждой точке которого определена его первая производная, можно представить в виде суммы потенциального и вихревого полей. Для двумерного векторного поля E =( E 1 , E ₂, 0) это разложение имеет вид

E ' = - V_±y + [ V_± , Y ],

где V_± = (V_t, V₂), ф - скалярный и Y - векторный потенциалы. Соответствующей калибровкой можно добиться, чтобы векторный потенциал имел только одну компоненту, продольную: Y = (0, 0, _Фз = y ). Используя линеаризованную систему (1)–(4), можно выразить компоненты возмущенного поля через потенциалы φ и ψ:

1         1 Ю ²

x    V3 +---- - тороидальный и полоидальный g3   3   p A2

продольные операторы, S=(γP0/ρ0)1/2 – скорость звука в плазме, A = Bo / ^4пр0  - альфвеновская скорость. Подействуем оператором Lˆ слева на (6) и

E_x = -V^ + ik y ,

E₂ =- ik₂ y-Vy , E₃ = 0,

c g 1

1 = ю gg

V 3 k 2 y- A V , y ,

V      gg   J

b. =

^ю pg

V 3

V^ — ik^-gU y ,

B 3

c g 3

i ю^ g

V 1 ^P_ V , y- k 2 '^ y ,

v ₁

—

v 2 =

g ₂

cg

—- ik 2 Y ⁺ -j= ^V 1 Y ,

P^B 0 V       gg    J

-

cp

— V^- ik₂ -g L y ,

B

⁰ V

V 3 =— i — V 3 P' , ЮР 0

возмущенное давление определяется уравнением

I 0 P’ = i Y cP

X

X

ik 2 YV i Sk + V i p’ V i Y - k 2 - PP L- y B ₀         B ₀           pB ₀

где обозначено p = ^ g ₂ / pg ,

L - l ₊ i P   PP^

^L0 = ^{1 +}   2 Г~ ^V 3          ^V 3 .

^ю gg    P 3 P 0

Домножим (5) на ik 2 B 0 /ρ 0 , (6) – на B 0 /ρ 0 , продифференцируем его по x ¹ и вычтем получившиеся уравнения одно из другого. В результате получим

V_x Ц Vy- k ₂ ²

Г.

^l p ^y+ V

s ² y

,  ------ X

A   g ₁ g ₂

xV, In B _oV, In

k 1

B 0 J

подставим в получившееся уравнение компоненты возмущенного поля из (8)–(10). После некоторой перегруппировки слагаемых получаем

МП L 20^ Ay + s ² Ay +ю ² y =

4 nP 0   ⁰ 4?₃

= - iB r '^ 1^ 0 B 0 L- T V 1 Y-ik 2 S ²Y 4^ V , In^ ^p 3 ^{p 0}.

4 ⁿ k 2 p ₀                   gg       B 0

где введены аналоги оператора Лапласа:

a = ^Pt^z Vi ^gr= Vi

k ₂        g ₂      g ₁

^- p 2 ^V1 j g ^V 3 V g

a =

X

B 1

—- „    X

°

P 0    g ₁ g ₂

V, pPP Lv -

¹ B 0     ¹

kf PL p B0

nP P Lv   ^{p 0}

^{P 3 p} 0    B 0 4^g i j

Уравнения (12) и (13) образуют замкнутую относительно потенциалов φ и ψ систему уравнений. При переходе к однородной плазме правые части этих уравнений обращаются в нуль. Оператор в левой части (12) дает дисперсионное уравнение для аль-фвеновских волн: ю ² = k 2 A ², где k 2 = k 2 / Р з, а оператор в левой части (13) – дисперсионное уравнение для магнитозвуковых волн:

ю ⁴ -ю ² k ²( A ² + S ²) + k ² k 2 A ² S ² = 0, (14) где k ² = k 2 + k 2 , k 2 = k 2 / g_x + k 2 / g ₂. Таким образом, можно полагать, что альфвеновские колебания описываются скалярным потенциалом φ, а магнитозвуковые – продольной компонентой ψ векторного потенциала. В неоднородной плазме правые части уравнений (12) и (13) описывают взаимодействие этих ветвей МГД-колебаний.

Если выполняется одно из неравенств: S ^ A , A ^ S, | k | |<С| k _± |, из (14) можно получить следующие приближенные дисперсионные уравнения:

ю2 « k2 (A2 + S2) для БМЗ-волн, ю2 « k2C2 для ММЗ-волн, где Cs2 = A2 S2 / (A2 + S2). Из вида дисперсионного уравнения видно, что Cs представляет собой фазовую скорость распространения ММЗ-волн.

Для последующих численных расчетов распределение параметров фоновой плазмы вдоль силовой линии магнитного поля рассчитано по численной модели плазмосферы Кринберга–Тащилина, подробно представленной в [Кринберг, Тащилин, 1984]. На рис. 2

g ₂

= ik ² v, p. -g k- L_p -g kVj

ˆ ^{g 1}

ю

Y ,

?      1         p      .m 2    ~      1  „  1

где LT = ^V3 ^V3 + p ,2 , LP = I--V3  X gg  A  gp

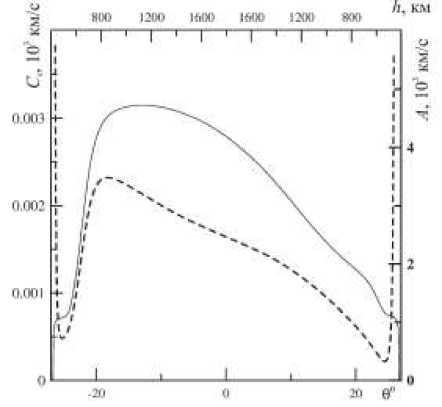
Рис. 2. Распределение альфвеновской скорости A (θ) (штриховая линия) и скорости ММЗ-волн C _s (θ) (сплошная линия) вдоль силовой линии, пересекающей ионосферу Земли в Северном полушарии над территорией Японии (37° N, 138° E), в 11:00 UT 14 июня 2008 г.

приведено распределение альфвеновской скорости A и скорости C _s вдоль магнитной силовой линии, пересекающей ионосферу Земли над территорией Японии (37° N, 138° E), в 11:00 UT 14 июня 2008 г. Видно, что по крайней мере одно из указанных выше неравенств ( S ^ A ) выполняется практически по всей длине силовой линии. Расчет параметров среды в Северном и Южном полушариях проводился от высоты 80 км до вершины силовой линии (~1700 км). Обратим особое внимание на резкий рост A и убывание C _s на высотах h <400 км. Это связано с резким уменьшением концентрации и температуры ионов плазмы на высотах ниже F2-слоя ионосферы. Сильная асимметрия профилей A и C _s в Северном и Южном полушариях обусловлена разными граничными условиями на ионосферных концах силовой линии: ионосфера в Северном полушарии освещена Солнцем, а в Южном уже нет.

В рамках данного приближения дисперсионное уравнение для ММЗ-волн очень похоже на дисперсионное уравнение для альфвеновских волн. При этом фазовая скорость ММЗ-волн, так же как и альфвеновских волн, направлена вдоль силовых линий магнитного поля. Поскольку потенциал ψ описывает как быстрые, так и медленные магнитозвуковые волны, в линейном приближении его можно представить в виде суммы ψ = ψ +ψ , где составляющая ψ_F связана с БМЗ-волной, а ψ – с ММЗ-волной. Можно показать, что в однородной плазме для ММЗ-волн (φ=0, ψ = ψ ) ) выполняются следующие соотношения:

k ^{2 2}

(P'+Pm)/P'~(P'+Pm)/Pm= ||2 2A 2, где P =B B /4π – возмущенное магнитное давление. Следовательно, для колебаний с | k| | k| полное давление в ММЗ-волне практически не возмущается:

P ' + BB /4 π≈ 0.                      (15)

В рамках рассматриваемой модели магнитосферы характерные собственные частоты основных гармоник стоячих альфвеновских и ММЗ-волн различаются более чем на два порядка величины. Это означает, что взаимодействие альфвеновских и ММЗ-волн на замкнутых силовых линиях практически отсутствует, поэтому при исследовании структуры ММЗ-колебаний, описываемых уравнением (13), будем полагать в его правой части φ=0. Для БМЗ-волн с периодами колебаний более 10 мин, рассматриваемыми в настоящей работе, вся магнитосфера представляет собой область непрозрачности, потому будем считать, что во внутреннюю плазмосферу БМЗ-волны из солнечного ветра практически не проникают и ψF=0. Для ММЗ-волн в плазмосфере из (13) получаем уравнение

^{B 0 g 3} L ^ˆ ₀ ^{B 0} ∆ψ _S + S ² ∆ψ _S +ω ² ψ _S = 0.       (16)

4 πρ ₀       g ₃

Граничное условие для функции ψS на ионосфере было получено в работе [Leonovich et al., 2006]. Вертикальные движения атмосферы возмущают проводящий слой ионосферы и генерируют в нем сторонние токи. При этом граничное условие для функции ψS имеет вид

( ± )

ψ S _x 3 _{= x} 3 = i _{( ± )},                                         (17)

ΣP где координата x3 соответствует точкам пересечения силовой линии с ионосферой Северного и Южного полушарий соответственно, Σ – интегральная педер-сеновская проводимость ионосферы, а функция J(±) ≡J(x3 =x3) связана с плотностью сторонних токов соотношением

∆

∆_⊥ J = ∫ ( ∇× j _ext) _zdz , 0

где ∆ = ∇ ² +∇ ² – поперечный оператор Лапласа, Δ – толщина проводящего слоя ионосферы.

Характерные масштабы основных гармоник стоячих ММЗ-волн, возбуждаемых прохождением терминатора по ионосфере, в направлении вдоль магнитных силовых линий (по координате x3) и поперек магнитных оболочек (по координате x1) много больше их азимутального масштаба (по координате x2), определяемого шириной фронта терминатора. Cледовательно, решение (16) можно искать методом разных масштабов. В главном порядке, оставляя в (16) только слагаемые, пропорциональные большому азимутальному волновому числу k2, получаем pρ0     gP0σ

^P 0 ^{σ B} 0   ^{3 g} 3 ^ρ 0

^{B 0} ψ S + ^ω ₂ ψ S = 0.      (18)

g ₃       C s

Решение этого уравнения можно представить в виде

ψS=V(x1)S(x1, x3), где функция V(x1) определяется источником рассматриваемых колебаний и описывает распределение их амплитуды поперек магнитных оболочек, функция S(x1, x3) описывает распределение потенциала ψS вдоль магнитной силовой линии и определяется уравнением (18). Функция S(x1, x3) зависит от координаты x1 как от параметра. Для дальнейших расчетов удобно ввести функцию H (xv, x3) = 5 (x1, x3) Bо / ( g2 vZ), которая описывается уравнением

^«( x ¹^) ^ H + ^ 2 a ( x ',0 H = 0,          (19)

где dt = g^dx3 - элемент длины вдоль силовой линии (см. рис. 1), a(x1,^) = p3 ^gg / р0 . Основные компоненты поля азимутально-мелкомасштабных ММЗ-волн можно представить в виде

E = ik2vs, E2 = -V Vs, E3 = 0,(20)

B l =- ic - — g= ViVs,

1     го p ae

B2 = k 2-p ^ Vs,(21)

го   ae g_g

- k ²

^B 3 = ^- i V s ,

^ГО g 2

а в качестве граничного условия используем (17), при этом будем полагать ионосферу идеально проводящей (L_p ^ ^ ). Отсюда имеем H ( x ¹,£_± ) = 0, где

^+ - точки пересечения силовой линии с верхней границей проводящего слоя ионосферы в Северном и Южном полушариях.

В первом порядке теории возмущений можно получить уравнение для функции V ( x ¹), а в граничном условии (17) учесть отличную от нуля правую часть. Решая это уравнение, можно определить распределение амплитуды V ( x ¹), выраженной через амплитуду сторонних токов в ионосфере. Полностью эта процедура представлена в работе [Kozlov, 2008]. К сожалению, неизвестны амплитуды сторонних токов в проводящем слое ионосферы, поэтому ограничимся решением нулевого приближения, описывающего продольные собственные функции Hn ( x^xA

Решение (19) с такими граничными условиями представляет собой ряд собственных функций H_n ( x ¹,^) и соответствующих им собственных значений частоты Ω_{S n} ( x ¹), где n =1, 2, 3, … – продольное волновое число. В двух первых порядках ВКБ-приближения решение (19), удовлетворяющее

указанным выше граничным условиям, имеет вид

H n = C n a C s / ^ n

sin

^V 1 =

c

B J g T

^V 1 V s ,

^ S n j dt '/ C s -

v 2 =

ik c

^B о V g 3

V S ,

^v 3

i S £ p ‘ гор₀ 51

где C_n – произвольная константа, Ω_{S n} =π n / t _s, t _s – время пробега вдоль силовой линии с фазовой скоростью ММЗ-волн между магнитосопряженными ионосферами:

+ ts = j de. -/ cs.                                            (26)

Для определения возмущенного давления используем приближенное соотношение (15), которое вместе с (21) и (22) дает следующее выражение для продольной компоненты скорости колебаний плазмы:

1 d     .1 d BB v = v. /ig. = -ip *г°t=-

¹¹      ^        гор о ae      гор о ae 4 п Дд₃

Линеаризуя уравнение (3), для возмущенной плотности получим выражение

р ’ = ^- i

1 d

Таким образом, из вида решения (25) следует, что вблизи ионосферы достаточно большую для регистрации амплитуду будут иметь только те компоненты поля стоячих ММЗ-волн, которые имеют f ⁵ пучность в проводящем слое ионосферы I-- Vs

V  d^

Как видно из (20)–(24), такими компонентами поля являются B , v || и ρ ' . Для n -й гармоники стоячих ММЗ-волн имеем в ВКБ-приближении

^го V g 1 g 2 ^d£

ggTi р о v ||

которое является основой для определения колебаний концентрации плазмы.

v n = w^ 0^ ^р о

cos

Q s n j de '/ C s -

Определение компонент поля ММЗ-волн в ВКБ-приближении

Для того чтобы получить качественное представление о структуре основных компонент поля рассматриваемых ММЗ-колебаний, решим уравнение (13) в ВКБ-приближении. Его решение можно найти, используя методы теории возмущений.

В нулевом порядке мы получаем уравнение (19),

где w ( x ¹) = C V ( x ¹) ck 2 / 4 nQ ^3/2 ( x ¹) . Возмущение плотности плазмы определяется уравнением (24) при v || = v || _n и ω=Ω_{S n} , а для основной компоненты возмущения магнитного поля азимутальномелкомасштабных ММЗ-волн имеем

B l * B y = B 2 / 4? 2 = V |Os п В о 4g / k 2 A ².

До сих пор мы не учитывали затухание ММЗ-колебаний. Выражение для коэффициента

затухания можно получить в рамках кинетической теории (см., например, [Leonovich et al., 2006]), величина коэффициента зависит от соотношения температуры ионов и электронов (в случае двухкомпонентной плазмы). В плазмосфере, где температура электронов выше температуры ионов ( T _e≈2 T _i), декремент затухания ММЗ-колебаний достаточно мал, поэтому они могут образовывать стоячие волны. Однако в среде с T e <  T i декремент затухания сопоставим с частотой колебаний, поскольку фазовая скорость ММЗ-колебаний близка тепловой скорости ионов среды. В результате за счет затухания Ландау энергия ММЗ-колебаний теряется при распространении вдоль силовых линий магнитного поля, в то время как потеря энергии магнитосферных альфвеновских колебаний происходит на концах силовых линий за счет омического нагрева ионосферной плазмы.

Оставаясь в рамках МГД-теории, введем декремент затухания в виде мнимой добавки к частоте ω→ω– i ε. Поскольку генерация ММЗ-колебаний происходит в области прохождения солнечного терминатора, учтем существование сторонних токов на этой границе, а в магнитосопряженной ионосфере выберем однородное граничное условие:

^ s - iJ\„ „/Z_r|,.,„ = C o Vsl„_ - °,       (27)

где     соответствует локальной области ионосферы, где проходит солнечный терминатор, а     – магнитосопряженной области ионосферы.

Тогда в первых двух порядках ВКБ-приближения по продольной координате с учетом граничных условий (для определенности положим lST-l _) получим следующее решение:

A(£) sin( to . ( T o -т (1)))

S ° A(t—)     sin(to*t0)      , d£ где т(1) - [ —, т° — t(€+),

C s

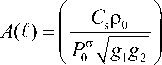
to* - to- i г .

Перейдем теперь к результатам численных расчетов спектра и структуры основных компонент поля колебаний стоячих ММЗ-волн.

Результаты численных расчетов и их обсуждение

Все численные расчеты проведены для события 14 июня 2008 г., рассмотренного в [Afraimovich, 2009b], когда над территорией Японии регистрировались колебания ПЭС, связанные с прохождением терминатора в магнитосопряженной ионосфере. В качестве примера рассмотрена силовая линия, пересекающая Северное полушарие в точке с координатами 37° N, 138° E. Расчет параметров среды производился по численной модели [Кринберг, Тащилин, 1984]. При численных расчетах использована система координат (a, φ, θ), связанная с силовыми линиями дипольного магнит-ного поля (см. рис. 1). Здесь a – экваториальный радиус силовой линии, φ – азимутальный угол, θ – широта, отсчитываемая от экватора. Длина радиус-вектора точки на силовой линии в этой системе координат имеет вид r=acos2θ, а элемент длины d£ — a cos 0V1 + 3sin2 0d0.

Напряженность дипольного магнитного поля определяется уравнением

Bo (a, 0) — Bo (a0 / a)3 V+ + 3sin2 0 / cos6 0, где B – напряженность магнитного поля на силовой линии с экваториальным радиусом a0 (на поверхности Земли a0=RE, B =0.32 Гс). Компоненты метрического тензора в данной системе координат имеют вид gx — cos6 0 / (1 + 3 sin2 0), g2 — a2 cos6 0.

Распределение A (θ) и C _s(θ) в 11:00 UT 14 июня 2008 г. вдоль рассматриваемой силовой линии представлено на рис. 2.

Мы сравним численно найденные решения уравнения (19) с однородными граничными условиями на ионосферах Северного и Южного полушарий, H ( x ¹,^_±) — 0, с аналитическими результатами, полученными в ВКБ-приближении.

Суточный ход периодов первых шести гармоник стоячих ММЗ-волн на указанной выше силовой линии представлен на рис. 3. Обращает на себя внимание сильное отличие периода колебаний основной

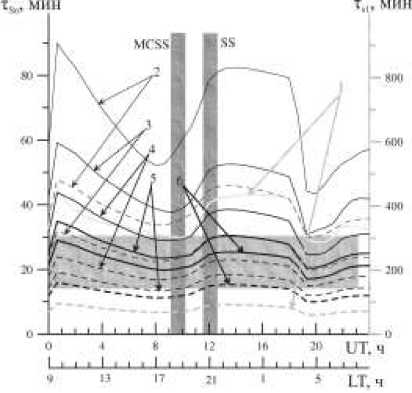
Рис. 3 . Суточный ход периодов колебаний первых шести гармоник стоячих ММЗ-волн 14 июня 2008 г. на силовой линии, пересекающей ионосферу в точке 37° N, 138° E. Штриховые линии – периоды колебаний в ВКБ-приближении, сплошные линии – периоды, полученные из численного решения уравнения (19). Период колебаний основной гармоники τ _s1 показан серым цветом (вертикальная ось справа). Горизонтальная серая полоса – диапазон периодов зарегистрированных колебаний TEC. Вертикальные серые полосы – характерные промежутки времени прохождения терминатора в точке наблюдения (SS) и в магнитосопряженной точке (MCSS).

гармоники (~300–400 мин) от периодов колебаний всех остальных гармоник (<90 мин). Различие периодов колебаний, рассчитанных численно и в ВКБ-приближениинии, уменьшается с ростом номера гармоники n . В диапазон периодов колебаний ПЭС, зарегистрированных в наблюдениях [Afraimovich, 2009b], попадают гармоники с n =4, 5, 6. Учитывая, что в проведенных наблюдениях колебания с периодами больше 30 мин обрезались, можно ожидать присутствия и более низкочастотных гармоник, однако их трудно выделить на фоне динамических эффектов, связанных с движением спутников GPS.

Для построения распределения амплитуды компонент поля ММЗ-волн необходимо задать амплитуду какой-либо их компоненты в любой точке на силовой линии. К сожалению, прямые измерения амплитуды колебаний в области генерации совместно с наблюдениями колебаний ПЭС над территорией Японии отсутствуют. Однако в работе [Onishi, 2009] приведены данные одновременных наблюдений колебаний ПЭС и продольной компоненты колебаний плазмы v || на спутнике DEMETER, пролетавшем над областью колебаний ПЭС на высотах 650–700 км. Безусловно, нельзя быть полностью уверенными в том, что зарегистрированные в [Onishi, 2009] колебания ПЭС представляют собой стоячие ММЗ-волны. Тем не менее мы воспользуемся полученными в работе [Onishi, 2009] соотношениями для калибровки рассматриваемых нами ММЗ-колебаний. При нескольких пролетах над территорией Северной Америки спутником DEMETER были зарегистрированы колебания v || с амплитудами 20–80 м/с при соответствующих колебаниях ПЭС с амплитудами 0.1–0.6 TECU (1 TECU = 10¹⁶ м^–2).

Для последующих расчетов мы зададим амплитуду колебаний |v|||=50 м/с на высоте 660 км. Солнечный терминатор возбуждает ММЗ-колебания в широком диапазоне частот, определяемом характерными длительностями переходных процессов в ионосфере и атмосфере. В данной работе мы будем предполагать, что в спектре регистрируемых колебаний доминируют колебания какой-то одной гармоники, так что задаваемая амплитуда v|| определяет колебания именно этой гармоники. Распределение v|| вдоль магнитной силовой линии для 4-, 5-, 6-й гармоник стоячих ММЗ-волн представлено на рис. 4. Наиболее интересной особенностью этих колебаний является резкий рост их амплитуды на несколько порядков величины на высотах h<400 км. Как следует из (23), это связано с резким уменьшением ρ0 (см. также рис. 2). Используемая в данной работе модель среды не учитывает влияния вязкости среды и столкновений заряженных частиц с нейтралами. Однако можно утверждать, что даже в реальной плазмосфере рост амплитуды продольной скорости будет значительным. Это, в свою очередь, должно приводить к периодическому высыпанию заряженных частиц в F2-области ионосферы, что может сопровождаться свечением нейтральной компоненты на этих высотах. Если рассматривать в качестве возможного источника таких колебаний прохождение терминатора в магнитосопряженной ионосфере, наиболее благоприятными для наблюдения свечений в Северном полушарии должны быть предутренние один-два часа в периоды времени, близкие зимнему солнцестоянию. В это время терминатор в магнитосопряженной области ионосферы Южного полушария максимально опережает терминатор в Северном полушарии.

Рассмотрим теперь распределение амплитуды поперечной компоненты магнитного поля колебаний вдоль силовой линии. На рис. 5 для 4-, 5-, 6-й гармоник

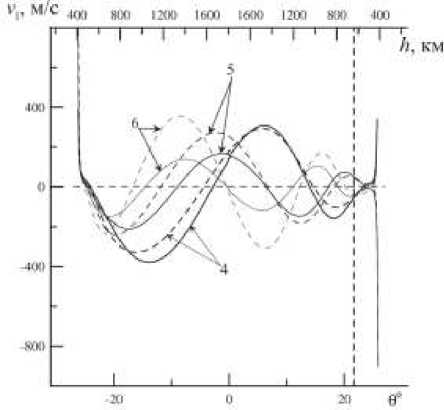
Рис. 4 . Распределение продольной компоненты скорости v || для 4-, 5-, 6-й гармоник стоячих ММЗ-волн вдоль силовой линии, пересекающей ионосферу в точке 37° N, 138° E в 11:00 UT 14 июня 2008 г. Штриховые кривые линии – распределение амплитуды в ВКБ-приближении, сплошные линии – амплитуда v || , полученная из численного решения уравнения (19). Штриховая вертикальная линия – высота калибровки расчетных значений v || по данным спутниковых наблюдений (| v || |=50 м/с на высоте h =660 км).

В,. ИТ.Ч ^ адд |2on 1WN| |ОТ |200  „00   400

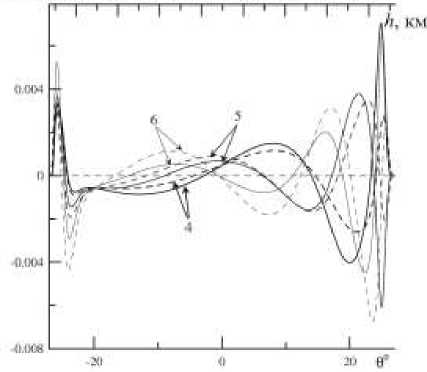
Рис. 5 . Распределение основной компоненты магнитного поля рассматриваемых колебаний B _y с азимутальным волновым числом m =20 для 4-, 5-, 6-й гармоник стоячих ММЗ-волн вдоль силовой линии, пересекающей ионосферу в точке 37° N, 138° E в 11:00 UT 14 июня 2008 г. Штриховые кривые линии – распределение амплитуды в ВКБ-приближении, сплошные линии – амплитуда B _y , полученная из численного решения уравнения (19).

стоячих ММЗ-волн показано распределение амплитуды By -компоненты поля ( B = B ₂ / ^g - физическая компонента), которая является доминирующей вблизи ионосферы. Как следует из (9), амплитуда этой компоненты обратно пропорциональна азимутальному волновому числу m . Исходя из оценки характерной ширины фронта терминатора (один-два часа), при расчете выбрано m =20. B y достигает максимальной амплитуды на высотах ниже 400 км и не превышает 0.008 нТл. Это означает, что выделить колебания в магнитном поле на фоне естественных шумов практически невозможно.

Рассмотрим колебания электронной концентрации в стоячих ММЗ-волнах. В использованной модели среды плазма состоит из нескольких сортов ионов. В приближении идеальной МГД, использованном в расчетах структуры стоячих ММЗ-волн, плотность квазинейтральной плазмы определяется как р = mn, где n = ^ na - полная плотность ионов, α m = ^mana / n — приведенная масса частиц плазмы, α а суммирование проводится по всем сортам частиц. Используя (24), определим ρ' через найденные выше распределения продольной скорости v|| и, с учетом квазинейтральности плазмы, для возмущения электронной концентрации получим ne = n ’ = р'/ m.

Распределение амплитуды колебаний электронной концентрации n' для 4-, 5-, 6-й гармоник стоячих ММЗ-волн вдоль силовой линии представлено на рис. 6. Видно, что оно имеет резкие пики на высотах ~200 км в Южном полушарии и ~300 км – в Северном. Это обстоятельство позволяет оценить величину колебаний полного электронного содержания путем интегрирования n' вдоль магнитной силовой линии. Благодаря наличию резкого пика в распределении n' , величина

N енС б ) = J n ' dt

± на высотах h>400 км не должна существенно отличаться от амплитуды колебаний ПЭС, полученной при интегрировании вдоль луча, направленного от приемника GPS на спутник. Здесь знаки ± относятся к верхней границе проводящего слоя ионосферы в Северном и Южном полушариях соответственно, а интегрирование ведется вдоль магнитной силовой линии.

На рис. 7 представлено распределение N e|| (θ) для 4-, 5-, 6-й гармоник стоячих ММЗ-волн в южной и северной частях плазмосферы. Видно, что полученные таким образом амплитуды колебаний | N _e || |~0.4–0.8 TECU при h >400 км вполне соответствуют амплитудам колебаний ПЭС, зарегистрированных в [Onishi, 2009]. Это позволяет надеяться, что в работе [Onishi, 2009] также были зарегистрированы ММЗ-колебания. Амплитуды колебаний ПЭС, зарегистрированных в [Afraimovich, 2009b], на порядок ниже и составляют 0.01–0.04 TECU.

Заключение

Перечислим основные результаты данной работы.

• 1.    Получено уравнение, описывающее структуру поля азимутально-мелкомасштабных стоячих ММЗ-волн в дипольно-подобной магнитосфере. Получено как его аналитическое решение в ВКБ-приближении, так и численное решение для распределения параметров плазмы, соответствующих плазмосфере Земли.

• 2.    Определен спектр периодов колебаний основных гармоник стоячих ММЗ-волн на силовой линии, пересекающей ионосферу Земли в точке 37° N, 138° E, в 11:00 UT 14 июня 2008 г. В диапазон периодов

• 3.    Построены продольные (вдоль указанной выше магнитной силовой линии) распределения компонент поля ММЗ-волн, которые можно зарегистрировать вблизи ионосферы на низкоорбитальных спутниках ( V || , и ). Показано, что вблизи ионосферы поле стоячих ММЗ-волн представляет собой колебания плазмы в направлении вдоль фонового магнитного поля, практически его не возмущающие. Колебания скорости плазмы т и ее концентрации n' сдвинуты по фазе на π/2.

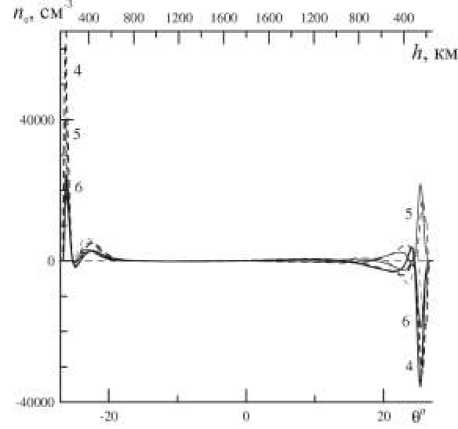
Рис. 6 . Распределение колебаний концентрации электронов n _e для 4-, 5-, 6-й гармоник стоячих ММЗ-волн вдоль силовой линии, пересекающей ионосферу в точке 37° N, 138° E, в 11:00 UT 14 июня 2008 г. Штриховые линии – распределение амплитуды в ВКБ-приближении, сплошные линии – амплитуда n _e , полученная численным решением уравнения (19).

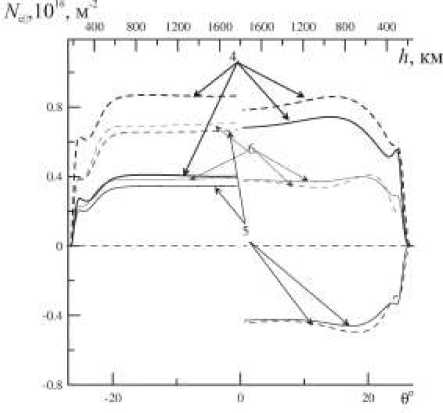
Рис. 7 . Распределение полного электронного содержания N _e || (θ) для 4-, 5-, 6-й гармоник стоячих ММЗ-волн вдоль силовой линии, пересекающей ионосферу в точке 37° N, 138° E, в 11:00 UT 14 июня 2008 г. Штриховые линии – распределение амплитуды в ВКБ-приближении, сплошные линии – амплитуда N _e || , полученная численным решением уравнения (19).

зарегистрированных колебаний, которые в [Afraimovich, 2009b] были интерпретированы как стоячие ММЗ-волны, из рассчитанных нами попадают 4-, 5- и 6-я гармоники.

Авторы благодарят А.В. Тащилина и Л.А. Леонович за расчет параметров фоновой плазмы, использованных в работе. Работа выполнена при частичной финансовой поддержке грантов РФФИ № 10-05-00113, № 12-02-00031 и программы Президиума РАН № 22 и Минобрнауки РФ (соглашение № 8699).