Генерация симиляритонных параболических импульсов в волоконно-оптических усилителях с растущим профилем хроматической дисперсии

сти. Для временной огибающей импульса u ( t , z ) справедливо следующее нелинейное уравнение Шредингера с переменными коэффициентами:

д u . P 2 (z ) д ² u d z ”^Z 2 d t²"

⁺ i Y ⁽ z ) | u|²

u = gu , 2

где z – координата вдоль волокна, t – время в бегущей системе координат, Y - параметр нелинейности волокна, g – инкремент усиления.

Представим параметры дисперсии и кубической нелинейности в виде Р ₂(z ) = Р _2йd ( z ) и Y ^(z ) = Y o r ^{( z} ) - где ^ 20 и Y o - значения соответствующих параметров на входе в световод, а d (0) = r (0) = 1 . Введем в уравнении (1) новые

переменную

^f = r d ^{( z}')^dz'

и огибающую им-

пульса A ( t , z ) = u ( t , z ) ^r ( z )/ d ( z ) . В результате для огибающей A ( t , z ) мы приходим к урав-

нению с постоянными дисперсией и нелинейнос-

тью, но неоднородным по длине усилением:

a A - i ft^ 8 2 A д^ 2 a t²

⁺ i Y o |A|² A =

Г( ^ ) A.

Здесь введен зависящий от переменной ^ эффективный коэффициент усиления:

П£) =

— д_ in d ⁽ ^ > d ( 5 ) d f r ( })'

Известно, что в активных световодах с нормальной дисперсией возможен самоподобный (симиляритонный) режим распространения импульса. Его особенность заключается в том, что огибающая импульса при достаточно больших пройденных расстояниях ( z >>  1/ g ) асимптотически стремится к параболической форме, мас-

штабирующейся с ростом координаты импульса [1-3]. Общий вид импульса параболической формы может быть записан в виде

A(t , 5 ) = A( ^ )G pa_ (t , 5 ) exp [ i ( ^ ( 5 ) + а ( 5 ) t ² ) ] , (4) где ^ ( 5 ) и 0 ( 5 ) – фаза и скорость ЧМ импульса, которая для симиляритона является постоянной величиной. Функция G_par ( t , 5 ) задает форму огибающей параболического импульса и определяется выражением

G par

' 71 - 17.'.

0 ,

t ^ T ^{( 5 )}, t >  ^T s ^{( 5 )} ,

где 2.T_s ( 5 ) — характерная длительность импульса параболической формы. Амплитуда и фаза асимптотического (при больших z ) параболического решения не зависят от начальной формы импульса, а определяются только начальной энергией импульса E ₀ и параметрами световода. В случае постоянных по длине световода усиления и нелинейности для больших длин распространения импульса мы можем записать следующие соотношения для амплитуды и длительности импульса [2]

gE о

A ( 5 ) =¹ , 2 ( — 0/2

_{( 5 )} = 6 _х;. / /2 ^g

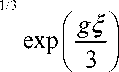
A 0

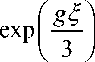
При больших значениях параметра 5 чирп импульса а ( 5 ) становится постоянной величиной а ₀ = Г /6 О ₂₀ , что может быть использовано как условие существования асимптотического решения уравнения (2) в виде ЧМ импульса параболической формы. Более детальный анализ (в том числе и с использованием известных вариационных методов), показывает, что эволюция чирпа асимптотически параболического импульса в световоде с постоянным усилением описывается уравнением [4]

⁸ / ¹ = - 2 а ² ( 5 ) ^ 20 + C E - e exp( Г 5 ) (,,

85 Ts (5)

где C – константа порядка единицы, зависящая от начальной формы импульса. Из уравнения (7) следует, что высокие значения начальной энергии импульса E 0 приводят к росту частотной модуляции а ( 5 ) и удалению от симиляритон-ного режима а ( 5 ) = const . Для минимизации искажений импульса и стабилизации его чирпа нами предлагается усиливать импульсы с некоторым начальным значением чирпа а (0) = а ₀ .

При этом выбором начальной энергии E 0 можно добиться выполнения условия 8 а ( 5 )/ 8 5 — 0 . Учитывая асимптотические соотношения (6), получаем, что для выхода на асимптотически параболический режим распространения с чирпом а ₀ величина начальной энергии импульса должна быть E ₀ ~ 2 а 2 P ₂₀ T³ ₀ / C — , где Т ₀ -начальная длительность импульса. С учетом этого соотношения условие существования асимптотического решения уравнения (2) запишется в виде

Г = 6 0 0 6 2 0 = 3 CE 0 - / О 0 Т 3 .       (8)

Это условие с учетом (3) для эффективного инкремента приводит к уравнению

^ ^ ^ ^- g ^ 2 ⁽ z ^{) + 6 О} 0 ⁶ 2 ²⁽ z ⁾ = ⁰ ,      (9)

8z где мы вернулись к координате z . Проводя решение этого уравнения (которое является уравнением типа Бернулли), находим вид профиля ДГС, который обеспечивает выход начального импульса на симиляритонную асимптотику:

О ₍ X =       g ^ 20 ^eXP⁽ gz ⁾

²       g ^{+ 6 а} 0 ° 20 ( ^eXP⁽ gz ^{) -} ! ) "      ⁽¹⁰⁾

Данный профиль ДГС обеспечивает постоянное вдоль световода эффективное усиление Г . Для пассивного световода c пренебрежимо малыми оптическими потерями (в случае g —> 0 ) мы приходим к известному результату [3]

О ( z ) = ^{6 20}          лп

^Р     1 + 6а„ P„ z        ⁽¹¹⁾

в соответствии с которым зависимость ДГС от координаты, удовлетворяющая условию существования симиляритона, должна иметь гиперболический вид.

Получение симиляритонных импульсов высоких энергий связано с проблемами, которые требуют своего решения. Условия на величину ДГС и инкремента усиления приводят, согласно (8) к тому, что усиливаемый импульс приобретает сильную частотную модуляцию с а ~ 1025 С-2. Столь высокое значение чирпа приводит к негативным последствиям. Во-первых, это приводит к уширению спектра импульса и выходу его из спектральной полосы усиления, во-вторых, высокий чирп искажает и разрушает импульс еще до его выхода на симиляритонную асимптотику. Таким образом, экспериментальный интерес представляет относительно высокое значение инкремента усиления световода при пониженной частотной модуляции импульса. Осуществить это возможно при помощи усиления импульса в световоде с постоянным инкрементом усиления g , профилем дисперсии (10) и эффективным усилением Г = 6а0320 << g. В этом случае выражение (10) задает при малых z быстрый и практически экспоненциальный рост ДГС, а при z » 1/ g - выходящий на предельное значение 32 = g /6а0. Технологически на сегодняшний день можно изготовить активные кварцевые одномодовые световоды длиной до нескольких км, нормальная ДГС которых растет в пределах 10-27 – 5.10-25 с2/м в соответствии с указанным профилем [5]. Принципиальное увеличение пределов изменения ДГС возможно при использовании фотонно-кристаллических волноводов или чир-пованных (с переменным периодом) волоконных решеток. Таким образом, представляется возможным получение мощных симиляритонных параболических импульсов в волоконно-оптических усилителях (например, эрбиевых) с высоким инкрементом усиления и увеличивающейся с длиной волокна нормальной ДГС. При этом импульс, по сравнению с генерируемым в усилителе с постоянной дисперсией, будет обладать более узким спектром и пониженной частотной модуляцией, что обеспечит его устойчивость.

Ниже приводятся результаты численного моделирования динамики импульса в волоконном усилителе. На основе соотношения (10) были построены профили нормальной ДГС, обеспечивающие динамический режим с выходом на параболическую форму огибающей импульса. Для найденных профилей нормальной ДГС с помощью SSFM–метода [9] проводилось численное моделирование уравнения (1) для следующих материальных параметров световода: 3 20 =10^-27 с²/м, g =0.5 м^-1, у = 1.33 х 10 3 (Вт • м) ’ ¹.

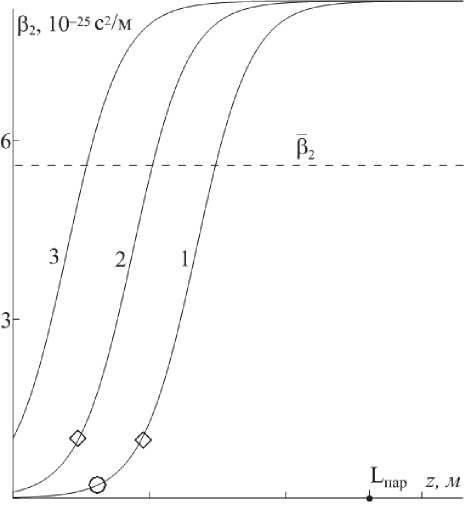
На рис. 1. приведены профили ДГС 3 2 ( z ) усилителя, полученные на основе (10) для различных входных значений ДГС. Реализуемые области изменения ДГС на длине усилителя лежат вне технологических пределов стандартных кварцевых волоконных световодов. Поэтому для практической реализации данной методики усиления необходимо использование либо волокон с радиальным W-профилем показателя преломления [5, 6], в которых возможно контролируемое изменение профиля ДГС, либо фотонно-кристаллических cветоводов, либо световодов с нанесенной решеткой показателя преломления с изменяющимся периодом (чирпованных решеток), нормальная ДГС которых может изменяться в достаточно широких пределах [7, 8]. Отметим, что в настоящее время успешно развиваются технологии получения активных световодов с управляемой гигантской дисперсией, достигающей значений а = 10 ’ 24 с²/м.

На следующих трех рисунках представлены временные зависимости изменения мгновенной частоты Д to ( t ) и огибающей импульса u ( t ) , оп-

0             10            20             30

Рис. 1. Профили ДГС, полученные на основе (10), усилителя с параметрами: g =0.5 м ’ ¹ , а = 10²³ с^-2,

3 20 = (0.1,1,10) Х 10 ² с²/м (кривые 1-3)

ределяющие эволюцию формы импульса при его распространении в усилителе. Указанные зависимости, полученные для усилителя с профилем дисперсии 1 (рис. 1), приведены на рис. 2. Кривые 1-3 на этом рисунке отвечают трем длинам распространения импульса: z = (18, 24, 26.8) м, пунктирные кривые - асимптотическим параболическим решениям уравнения (1). Для проведения численного моделирования в качестве входного импульса использовался гауссов импульс с временной огибающей ug(t) = TPexP(’t2/212 ’i«012), (12) несущей длиной волны л=1.557 мкм, длительностью t0 = 20 пс, скоростью частотной модуляции а0 = 1023 с-2 и пиковой входной мощностью P0 =1.4 Вт. При этом начальная энергия импульса составляла E0 = 49.6 пДж. Масштабные параметры – начальная дисперсионная длина L, = 102 / 320 и начальная длина нелинейности Ly = 1/УР0 при выбранных значениях материальных параметров удовлетворяют условию L3 >> Ly, что является необходимым для формирования параболических импульсов. Штриховая прямая на графике изменения мгновенной частоты отвечает ее линейному росту Дto = 2а01 в соответствие с асимптотикой фазы параболического импульса ^(z) = ^(z) + а(z) t2. Штриховым линиям для зависимости u(t, z) отвечают асимптотические решения уравнения (1):

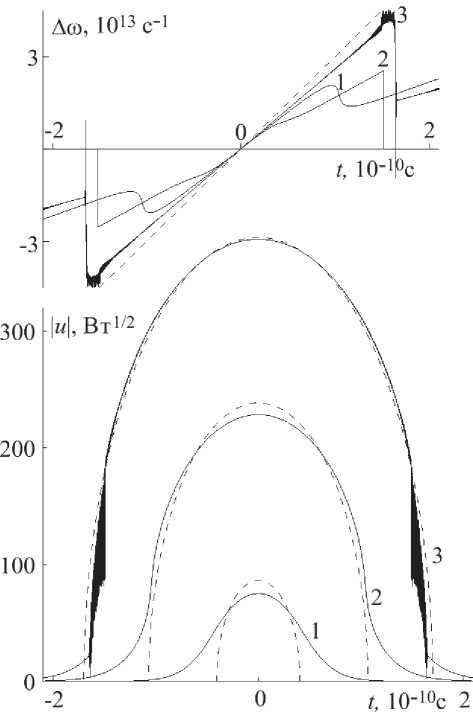
Рис. 2. Эволюция изменения частоты Д ю ( t ) и огибающей импульса u ( t ) в усилителе с увеличивающейся ДГС и длиной распространения z = (18, 24, 26.8) м (кривые 1-3); пунктирные кривые – асимптотические решения

₍. _А A exp g^^-ЖР^ u™ ⁽ t , z ) =;-----------------;------------7717?,

( 1 ⁺ ( « Д/ g Xexp gz H) )

~ ⁽ z ) = ^f f^{1 + 6} «^Р ( exp gz >¹¹ ] , ^A =¹ ( ⁶ «>МЖч/ Y )

«W» k g        )                '

Анализ полученных выражений показывает, что на начальной стадии распространения импульса совместное действие усиления, дисперсии и нелинейности приводит к его усилению практически с сохранением своей начальной формы (назовем эту стадию «линейной»). В дальнейшем совместное действие указанных факторов приводит к изменению формы импульса. Начиная с центральной части, происходит приближение формы огибающей импульса к параболической асимптотике. На пройденном расстоянии L _пар = 26.8 м форма огибающей импульса уже практически совпадает с асимптотической, а энергия импульса достигает величины E = 25 мкДж.

Отметим, что в процессе распространения импульса в усилителе происходит изменение чир-па по длине импульса, которое асимптотически стабилизируется и приводит к линейному росту мгновенной частоты и практически параболической форме огибающей. При выходе на асимптотику (кривые 3 на рис.2) на краях импульса видны зоны разрушения волнового фронта, т. е. происходит так называемый «wave-breaking» [10], связанный с обрушением функции мгновенной частоты. Это происходит из-за того, что на краях импульса более быстрые составляющие с большей частотной модуляцией «обгоняют» медленные.

На рис. 3 зависимости Д ю ( t ) и u ( t ) приведены для импульса в усилителе с растущей ДГС, длины распространения z = L пар = 26.8 м и различных значений начального чирпа: « ₀ = 0, 10 23 С ² (пунктирная и сплошная линии). Штриховой линии на зависимости Д ^ ( t ) отвечает временной рост мгновенной частоты с Дю = ( Г /3 P ₂₀) t = 2 « ₀ 1 . Для спектрально ограниченного входного импульса (с нулевым начальным чирпом) для режима усиления характерно отсутствие экспоненциальных хвостов, которые четко проявляются для импульса с начальным чирпом. При этом частотная модуляция (и, как следствие, ширина спектра) исходно чирпован-ного импульса после существенного его усиления значительно меньше, чем у исходно спектрально ограниченного импульса.

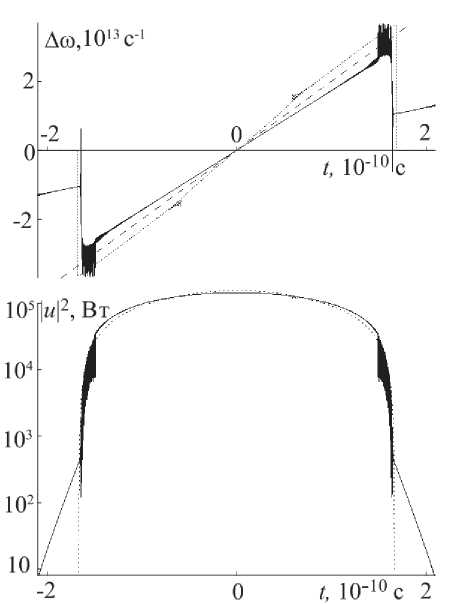
Рис. 3. Эволюция изменения частоты и огибающей импульса в усилителе с увеличивающейся ДГС; начальный чирп « ₀ = 0, 10 23 С ² (пунктирная и сплошная кривые), штриховая линия – зависимость Дю = Г t /3 Ж ₂₀ = 2 « ₀ 1

Для сравнения c полученными результатами нами было проведено моделирование динамики огибающей импульса в усилителе с постоянной ДГС, равной ее среднему значению Р ~ 5.5 Х 1 0 25 с 2 /м на длине распространения L пар = 26.8 м. В качестве начального выбирался гауссов импульс с пиковой мощностью P 0 =1.4 Вт и длительностью t ₀ = 20 пс. Результаты для зависимостей Д ю ( t ) и u ( t ) импульсов с начальным чирпом « 0 = 0,10 c представлены на рис. 4 (кривые 1, 2). Пунктирной кривой отвечают зависимости для импульса, прошедшего усилитель той же длины с профилем ДГС (10). Штриховая линия отвечает росту мгнове н ной частоты по линейному закону Д ю = ( g / 3 Р ) t . Видно, что усиленный импульс с отличным от нуля начальным чирпом в случае постоянной ДГС близок к параболической асимптотике только в центральной своей части. Отметим, что в этой области скорости ЧМ изначально чирпованных импульсов близки друг к другу и значительно снижены по сравнению со скоростью ЧМ исходно нечирпованного импульса.

На следующих двух рисунках приведена эволюция спектра импульса в усилителе с увеличивающейся и постоянной ДГС. В случае увеличивающейся дисперсии (рис. 5) зависимость спект-

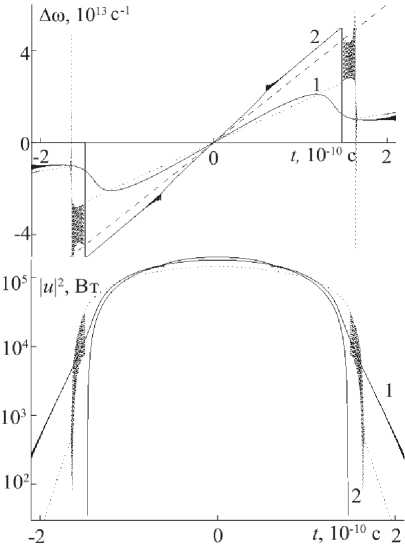
Рис. 4. Эволюция изменения частоты и огибающей и мпульса в усилителе с постоянной ДГС Р = 5.5 - 10 25 с²/м ; начальный чирп « ₀ = 0, 10 23 c ² (кривые 1, 2), пунктирная кривая – импульс после усилителя с профилем ДГС (10), штриховая лин и я - зависимость

Дю = ( Г /3 Р ) t

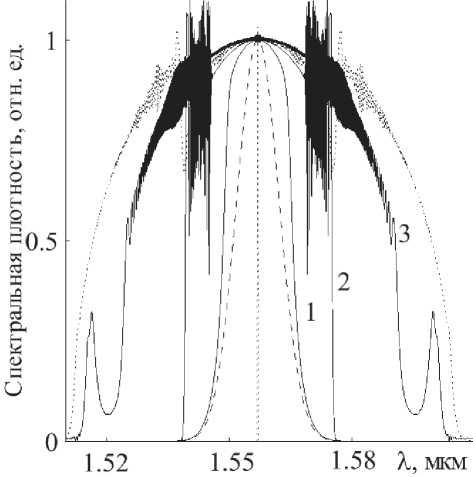
Рис. 5. Эволюция спектра импульса в усилителе с увеличивающейся ДГС: z = (18, 24, 26.8) М (кривые 1-3), штриховая линия - спектр входного гауссового импульса, пунктирные линии – спектры входного и выходного (на длине Lпар = 26.8 м) импульса без начального чирпа ральной плотности от длины волны получена для импульсов, прошедших в световоде расстояния z = (18,24, 26.8) м (кривые 1-3). Штриховой линии отвечает спектр начального гауссового импульса (12) с начальным чирпом «0 = 1023 с-2. Пунктирным кривым отвечают спектры входного и прошедшего расстояние z = 26.8 м импульсов без начального чирпа. Видно, что на начальном этапе усиления, где импульс практически сохраняет гауссову форму, спектр также практически не изменяется. При дальнейшем распространении импульса совместное действие нелинейности и дисперсии приводит к уширению спектра и искажению его формы. Это выражается в формировании по краям спектра интенсивных низко- и высокочастотной компонент. При дальнейшем приближении к параболической асимптотике центральная часть спектра выравнивается и также сходится к форме близкой к параболе, что соответствует симиляритонной модели усиления. Выделяющиеся компоненты отвечают «хвостам» импульса с частотной модуляцией, связанной с начальным чир-пом. Ширина спектра импульса на длине Lпар = 26.8 м составляет ДХ ~ 60 нм, что лежит в пределах полосы усиления эрбиевых оптических усилителей. Спектр импульса без начального чирпа имеет существенно большую ширину - ДХ = 80 нм.

На рис. 6 представлены спектры импульсов в световоде с постоянной ДГС Р ₂ = Р ₂ = 5.5 Х 10 ²⁵ с²/м и длиной распространения L_. = 26.8 м. Зависимостям 1, 2 отвечают пар

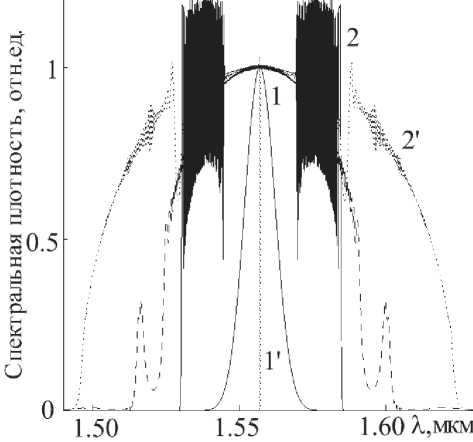
Рис. 6. Эволюция спектра импульса в усилителе с постоянной ДГС на длине м: кривые 1 и 2 – спектры входного и выходного импульсов с начальным чирпом , и – спектры входного и выходного импульсов без начального чирпа; штриховая линия – спектр выходного импульса с начальным чирпом в усилителе с растущей ДГС спектры входного и выходного импульсов с начальным чирпом а0 = 1023 c 2, а зависимостям 1 и 2 - спектры входного и выходного импульсов без начального чирпа. Для сравнения на этом рисунке штриховой линией обозначен спектр импульса с начальным чирпом а0 = 1023 c 2 после распространения в усилителе с профилем ДГС (10). Отмечаем, что изначально чирпованный импульс, прошедший усиление с постоянной ДГС обладает немного меньшей шириной спектра по сравнению с импульсом, прошедшем усилитель с растущей ДГС. Импульс без начального чирпа после прохождения усилителя близок к параболической асимптотике, обладает значительно более высокой скоростью ЧМ и более широким спектром ( Д^ = 120 нм), чем изначально чир-пованный импульс. т.е. можно говорить, что практическое получение импульсов с подобной шириной спектра крайне затруднительно.

Важным свойством волоконного усилителя с растущей ДГС является наличие скейлинга, т.е. сохранение формы огибающей выходного импульса при изменении энергии начального импульса и соответствующем изменении начальной ДГС и длины усилителя. Действительно, на начальном этапе с почти экспоненциальным ростом ДГС усиление импульса происходит с сохранением гауссовой формы огибающей. При этом можно утверждать, что усиление для разных профилей ДГС эквивалентны, если при равных ее значениях усили- ваемые импульсы обладают одинаковыми энергиями. На рис.1 кружком отмечена точка профиля ДГС 1, усиление из которой эквивалентно усилению по профилю 2. Аналогично ромбами отмечены точки профилей 1 и 2, усиление из которых эквивалентно усилению по профилю 3. Так, при вводе гауссова импульса с энергией E0 = 496 пДж в усилитель с начальной дисперсией =10-26 с2/м (профиль 2) и длиной , где м, на выходе будет получен импульс с характеристиками, отвечающими кривой 3 на рис. 2. Область скейлинга ограничивается областью экспоненциального роста ДГС, т.е. . Проведенный анализ позволяет сделать вывод, что все результаты моделирования усиления по профилю ДГС 1 можно перенести на усиление более мощных начальных импульсов в усилителях меньшей длины и меньшего диапазона изменения ДГС, что представляет большой практический интерес.

Таким образом, в настоящей работе предложена методика формирования параболических импульсов в оптических усилителях с увеличивающейся ДГС. Вычислен профиль ДГС усилителя, обеспечивающий генерацию мощных асимптотически параболических импульсов с пониженным значением скорости частотной модуляции и контролируемой шириной спектра. В качестве начального предлагается использовать исходно чирпованный импульс с определенным значением начальной энергии. Применение этой методики возможно при использовании технологий фотонно-кристаллических cветоводов, волокон с чирпованными решетками или так называемых световодов-компенсаторов дисперсии с дисперсией групповых скоростей свыше 10-25 с2/м. Скейлинго-вые свойства модели могут быть также использованы для создания оконечного усилителя в каскадной схеме усиления и генерации импульсов высоких и сверхвысоких энергий.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральных целевых программ «Научные и научно-педагогические кадры инновационной России на 2009 - 2013 годы» и «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы»