Generalization of Magic Square (Numerical Logic) 3×3 and its Multiples (3×3) × (3×3)

Автор: B L Kaul, Ramveer Singh

Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa

Статья в выпуске: 1 vol.5, 2012 года.

Бесплатный доступ

A magic square of 3×3 and its multiples i.e. (9×9) squares and so on, of order N are composed of (n×n) matrix having filled with numbers in such a way that the totals sum along the rows ,columns and main diagonals adds up the same. By using a special geometrical figure developed.

Magic Square, Square Matrix, Integer, Required Sum

Короткий адрес: https://sciup.org/15010357

IDR: 15010357

Текст научной статьи Generalization of Magic Square (Numerical Logic) 3×3 and its Multiples (3×3) × (3×3)

Published Online December 2012 in MECS

The sum of three or its multiple square numbers in all direction can be achieved the same (equal) by using a figure starting a number from one end to the other end either clockwise or anti clockwise serially using a number once only, we can achieve this easily by placing the figures in four different position.

A magic square is an n×n matrix filled with the integers in such a way that the sum of the numbers in each row, each column or diagonally remain the same, in which one integer is used once only. Magic square and its related classes of integer matrices have been studied extensively and still it is going on. As we know, ancient India is the origin of numbers and its properties, then after it spreads all over the world. As ARYA BHATT gave zero (0) to the World.

The interested reader may consult the references there in [1, 2, 3, 4, 5]. But, the reader can easily extract that there is requirement of knowledge of algebra, number and its properties and many different branches of mathematics for magic squares.

Here, we start with 3×3 matrix and with the help of special geometry able to obtain a magic square only having the knowledge of sum and multiplication of integers.

For (3×3), any number fifteen (15) or above up to the infinity divisible by 3 and for (3×3) x (3x3) Three hundred sixty nine (369) lowest and up to the infinity, which is divisible by 9 respectively can be achieved as a sum of the numbers of 3×3 squares and 9×9 squares in all direction the same. By using 9 or 81 numbers serially and using an each number once only as below.

8	3	4	15
1	5	9	15
6	7	2	15
15	15	15	15

Fig. 1: A

6	5	10	21
11	7	3	21
4	9	8	21
21	21	21	21

Fig. 1: B

30	27	42	99
45	33	21	99
24	39	36	99
99	99	99	99

Fig. 1: C

II. Theory

III. Our Process

For the nine squares a figure have been devloped which can be put in the nine square cube and starting by the number got by devuding the sum by three (3) and subtracting a contest of four (4) or munliple of four (4) from it such as we want the sum of the numbers of 3×3 square should be 36 in all the direction.

Devide 36 by 3 we get 36 / 3 = 12. We can start by the number 12-4=8 or 12- (4+4) = 4.

The difference beetween the numbers use will be one for subtracting four (4) a constrint and difference of two for the subtrating of (4+4) two constraints and so on. i.e.:-

Sr = 36, a=8, d=1

11	10	15	36
16	12	8	36
9	14	13	36
36	36	36	36

Fig. 2:A

Sr=36, a=4, d=2

10	8	18	36
20	12	4	36
6	16	14	36
36	36	36	36

Fig. 2:B

We can have four combinations more by placing the figure in four diffent direction clockwise or anti clockwise

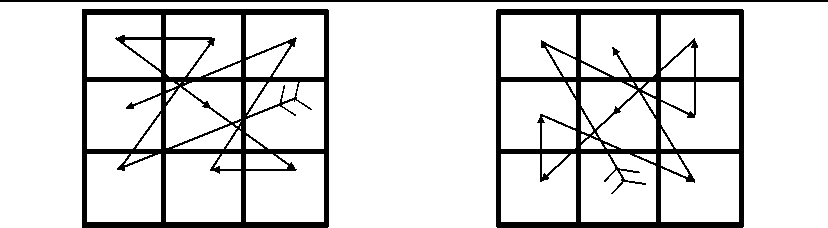
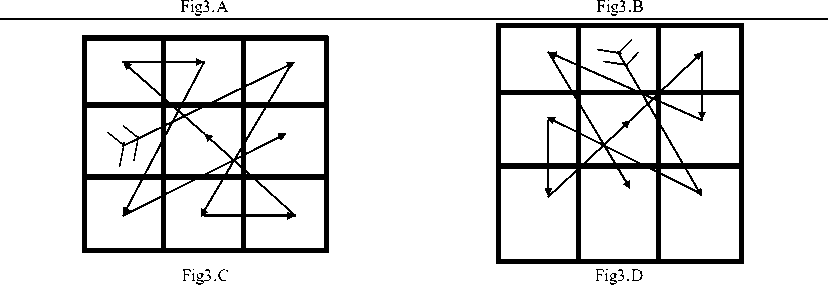
We also can have more combinetion possible for a higher sum required (SR) by subtracting multiples of constraints 4(four) from the number obtained by after deviding SR by 3.

Figures have been devloped and if these figures are placed on 3×3 squares or multiples of 3×3 i.e. 9×9 and so on. The sum of all the lines of any block in all direction can be achieved the same by using a number once only.

The figure used in 3×3 or its multiples is given below:-

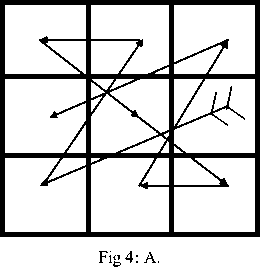
Any number 15 or above upto the infinity, which is devisible by 3 can be got in all the direction by putting the above figure in different position.

For example in 3x3 block we want sum required (SR) 147. The sum of all the numbers of each lines are same in all the direction, we must first devide it by 3.

As :- 147 ÷ 3 =49

Then subtract Four (4) a constraint number from it i.e. 49 – 4 =45

We can start with 45 in arthimatical progression that is 45, 46, 47 and so on to get 147 in all direction.

48	47	52
53	49	45	147
46	51	50
	147

Fig 5:

The same method can be used with other numbers having different equal difference beetween them like numbers

As above 147 One hundred forty seven can be achived with using other numbers also, having different equal difference beetween them, but the subtracting factor will be multiple of constrints that is four (4).

Like :-

SR = Sum Required a = Starting Number d = Difference beetween numbers

Table : 1

SR	Numbers	a	d
147	147 ÷ 3 = 49 – (4 ×1)	45	1
147	147 ÷ 3 = 49 – (4 ×2)	41	2
147	147 ÷ 3 = 49 – (4 ×3)	37	3
147	147 ÷ 3 = 49 – (4 ×4)	33	4
147	147 ÷ 3 = 49 – (4 ×5)	29	5
147	147 ÷ 3 = 49 – (4 ×6)	25	6
147	147 ÷ 3 = 49 – (4 ×7)	21	7
147	147 ÷ 3 = 49 – (4 ×8)	17	8
147	147 ÷ 3 = 49 – (4 ×9)	13	9
147	147 ÷ 3 = 49 – (4 ×10)	09	10
147	147 ÷ 3 = 49 – (4 ×11)	05	11
147	147 ÷ 3 = 49 – (4 ×12)	01	12

1, 2, 3, 4, 5, …………… Arthimatical Progression

1, 3, 5, 7, 9, …………… Geomatrical Progression

1, 4, 7, 10, 13, …………… Geomatrical Progression
1, 5, 9, 13, 17, …………… Geomatrical Progression

To get the sum one hundred and forty seven (147) the following starting numbers and difference will be them will be as :-

Table 2: Example of above table where SR = 147

Starting Number (a)	Number Used	d	SR
147 ÷ 3 = 49 – (4 ×1) = 45	45, 46, 47,…..	1	147
147 ÷ 3 = 49 – (4 ×2) = 41	41, 43, 45,…..	2	147
147 ÷ 3 = 49 – (4 ×3) = 37	37, 40, 43,…..	3	147
147 ÷ 3 = 49 – (4 ×4) = 33	33, 37, 41,…..	4	147
147 ÷ 3 = 49 – (4 ×5) = 29	29, 34, 39,…..	5	147
147 ÷ 3 = 49 – (4 ×6) = 25	25, 31, 37,…..	6	147
147 ÷ 3 = 49 – (4 ×7) = 21	21, 28, 35,…..	7	147
147 ÷ 3 = 49 – (4 ×8) = 17	17, 25, 29,…..	8	147
147 ÷ 3 = 49 – (4 ×9) = 13	13, 22, 31,…..	9	147
147 ÷ 3 = 49 – (4 ×10) = 09	09, 19, 29,…..	10	147
147 ÷ 3 = 49 – (4 ×11) = 05	05, 16, 27,…..	11	147
147 ÷ 3 = 49 – (4 ×12) = 01	01, 13, 25,…..	12	147

a = 45 & d = 1				a = 37 & d = 3
48	47	52		46	43	58
53	49	45	147	61	49	37	147
46	51	50		40	55	52
	147				147

Fig. 6: A From I	Fig. 6: B From III
a = 29 & d = 5	a = 21 & d = 7

	44	39	64		42	35	70
	69	49	29	147	77	49	21	147
	34	59	54		28	63	56
		147				147
Fig. 6: C From V					Fig. 6: D From VII
	a = 13 & d = 9				a = 5 & d = 11
	40	31	76		38	27	82
	85	49	13	147	93	49	05	147
	22	67	58		16	71	60
		147				147
	Fig. 6: E From IX				Fig. 6: F From XI

To start with arithmatical or geomatical progession with different equal differnce beetween each other, will have different lowest sum as:-

Table: 3

S. No.	Number Used	Difference beetween numbers	Lowest Sum	Differnce beetween Sums
1	1, 2, 3, ….	1	15	-
2	1, 3, 5, ….	2	27	12
3	1, 4, 7, ….	3	39	12
4	1, 5, 9, ….	4	51	12
5	1, 6, 11, ….	5	63	12
6	1, 7, 13, ….	6	75	12

In these cases the difference beetween the sums will be twelve (12) always and it will always be different for the same series if the starting number is changed like :-

Table: 4

S. No.	Number Used	Difference beetween numbers	Starting Number	Lowest Sum Obtained (SR)
1	1, 2, 3, ….	1	1	15
2	2, 3, 4, ….	1	2	18
3	3, 4, 5, ….	1	3	21
4	4, 5, 6, ….	1	4	24
5	5, 6, 7, ….	1	5	27
6	1, 3, 5, …..	2	1	27
7	2, 4, 6,…..	2	2	30
8	3, 5, 7, …..	2	3	33
9	4, 6, 8,…..	2	4	36
10	5, 7, 9,…..	2	5	39
11	1, 4, 7,…..	3	1	39

The total sum of nine numbers in any combination used for a given supposed sum remains always the same and is three times the given supposed sum.

Taking the advantage of this the starting number and differnce beetween them can be determine by using an equation devloped i.e. :- a + 4 d = SR ÷ 3

For example, Let SR = 60 then

a + 4 d = 60 ÷ 3

(i) Let d = 1, then

a + 4 × 1 = 60 ÷ 3 =20a = 20 – 4 = 16

(ii) Let d = 2, then

a + 4 × 2 = 60 ÷ 3 =20a = 20 – 8 = 12

(iii) Let d = 3, then

a + 4 × 3 = 60 ÷ 3 =20a = 20 – 12 = 8

(iv) Let d = 4, then

a + 4 × 4 = 60 ÷ 3 =20a = 20 – 16 = 4

16	12	32
36	20	4	60
8	28	24
	60		60

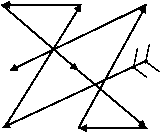
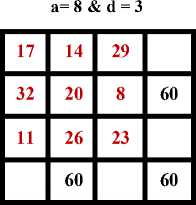
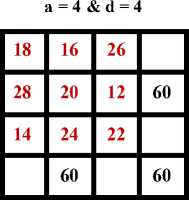
Fig. 7:

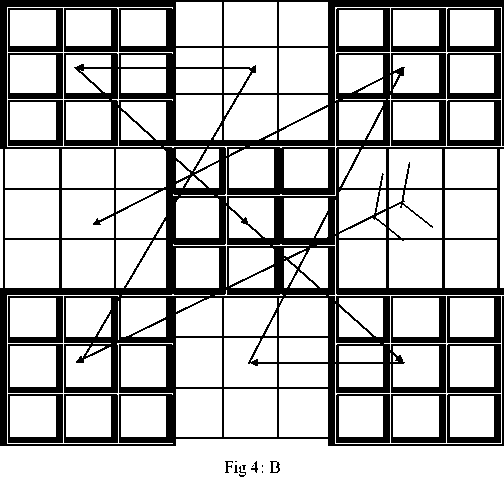
For the multiple of (3 × 3) × (3 × 3) i.e. (9 × 9) square the with same figure can be used in the way as 3 × 3 square.

A magical square of (9 × 9) squares, filled with numbers in such a way that the sum of all the lines add up the same in all direction vertically, horizentally and digonally using a number once only. Any number Three sixty nine (369) lowest and above upto the infinity which is devisible by 9 (nine) can be achived by placing the develop figure on the block of (9 × 9) squares starting a number got bydividing the (SR) sum required by nine (9) and then subtracting it by 40 (forty) a constraint or multiples of constant 40. We can easly get the starting number and difference kept beetween the numbers. By placing the figure of (3 × 3) on a block of (9 × 9) squares, nine times in the way shown below :-

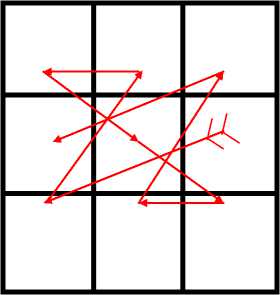
Fig 8: Magic Square with figure

31	30	35	22	21	26	67	66	71	369
36	32	28	27	23	19	72	68	64
29	34	33	20	25	24	65	70	69
76	75	80	40	39	44	4	3	8
81	77	73	45	41	37	9	5	1	369
74	79	78	38	43	42	2	7	6
13	12	17	58	57	62	49	48	53
18	14	10	63	59	55	54	50	46
11	16	15	56	61	60	47	52	51
369				369					369

Fig 9: Magic Square with Numbers

IV. Conclusion

In case of 3 × 3 nine square block the following method may be adopted to get the same sum in all direction. The number procured after deviding the sum required (SR) by three (3) should be kept in centre of the block and subtracting four (4) (constent number) or multiple of four (4) from it, to get the starting number and the differnece beetween the numbers used according the number of constrants subtracted. For one

constent the differnce beetween numbers will be one (1) and two constents it will be two (2) and so on.

For 9 × 9 (81) squares it will be same as above but, the constent number will be forty (40). In this case the lowest sum required (SR) will be 369 (Three hundred sixty nine) and the highest upto the infinity the number should be devisible by nine (9).

For different required sum (SR) starting number (a) and difference (d) beetween numbers will be different as follows :-

Table: 4

S. No.	SR	Number after deviding with nine (9)	a	d
1	369	369 ÷ 9 = 41	41 – 40 = 1	1
2	378	378 ÷ 9 = 42	42 – 40 = 2	1
3	720	720 ÷ 9 = 80	80 – 40 = 40	1
4	729	729 ÷ 9 = 81	81 – 40 = 41	1
			81 – 80 = 1	2
5	765	765 ÷ 9 = 85	85 – 40 = 45	1
			85 – 80 = 5	2
6	1089	1089 ÷ 9 = 121	121 – 40 = 81	1
			121 – 80 = 41	2
			121 – 120 = 1	3

Discussion on some applications:- The concept of balancing of Magical Squares with the help of developed geometrical figure is easy and perfect. This is a new concept of Magical Squares. It also can be used for moving bodies, Rotors, Cam Shaft, Crank Shaft and Wind Mill etc.

a) Cam Shaft: - Cam Shaft having eccentric cams at different angle and at different distance, Cam’s eccentric (out of center), but are balanced with equidistance and equal angle.
b) Crank Shaft: - The main Journals of the crank shaft in a line of center, but the crank pins are out of center at different angles and distances. It is balanced only by a geometrical concept
c) A high accurate balanced Wind Mill can be made by the concept of Magical Squares with accuracy (we are working on this project by using the concept of Magical Squares).

It is matter of further investigation towards, its possibilities of fruitfulness in the field of Engineering

[9] Ramveer singh & D. B. Ojha, (2011), Magic Square ORDES, World Applied Programming, Vol (1), No (4), October 2011. 252-255.

Список литературы Generalization of Magic Square (Numerical Logic) 3×3 and its Multiples (3×3) × (3×3)

Harold M. Stark. An introduction to number theory. MIT Press, Cambridge, Mass., 1978.
Joseph H. Silverman.The arithmetic of elliptic curves. Springer-Verlag, New York- Berlin, 1986.
Ezra Brown.Magic squares, finite planes, and points of inflection on elliptic curves. College Math. J., 32(4):260–267, 2001.
Agnew, Elizabeth H., “Two problems on magic squares,”Mathematics Magazine, 44 (1971),12–15.
Hanson, Klaus D.,“The magic square in Albrecht D¨urer’s“Melencolia I”:Metaphysical Symbol or mathematical pastime,” Renaissance and Modern Studies, 23 (1979), 5–24.
Ojha, B. & Kaul B.L., (2011). Generalization of 4x4 magic square. International Journal of applied engineering Research, Ddindigul, 1(4), 706-714.
Ojha, B. & Kaul B.L., (2011). Generalization of 5x5 magic square. Journal of Education and Vocational applied Research, 2(1), 18-23
Ojha, B. & Kaul B.L., (2011). Generalization of 6x6 magic square. Journal of Education and Vocational applied Research, 2(1), 18-23.
Ramveer singh & D. B. Ojha, (2011), Magic Square ORDES, World Applied Programming, Vol (1), No (4), October 2011. 252-255.

Статья научная

31	30	35	22	21	26	67	66	71	369
36	32	28	27	23	19	72	68	64
29	34	33	20	25	24	65	70	69
76	75	80	40	39	44	4	3	8
81	77	73	45	41	37	9	5	1	369
74	79	78	38	43	42	2	7	6
13	12	17	58	57	62	49	48	53
18	14	10	63	59	55	54	50	46
11	16	15	56	61	60	47	52	51
369				369					369

31	30	35	22	21	26	67	66	71	369
36	32	28	27	23	19	72	68	64
29	34	33	20	25	24	65	70	69
76	75	80	40	39	44	4	3	8
81	77	73	45	41	37	9	5	1	369
74	79	78	38	43	42	2	7	6
13	12	17	58	57	62	49	48	53
18	14	10	63	59	55	54	50	46
11	16	15	56	61	60	47	52	51
369				369					369

31	30	35	22	21	26	67	66	71	369
36	32	28	27	23	19	72	68	64
29	34	33	20	25	24	65	70	69
76	75	80	40	39	44	4	3	8
81	77	73	45	41	37	9	5	1	369
74	79	78	38	43	42	2	7	6
13	12	17	58	57	62	49	48	53
18	14	10	63	59	55	54	50	46
11	16	15	56	61	60	47	52	51
369				369					369