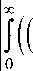Generalized Solvability of Initial-Boundary Value Problems for Quasihydrodynamic System of Equations in Weighted Sobolev Spaces

Introduction. We consider a quasihydrodynamic system of equations in the case of a weakly compressible fluid:

du              1„ where G is bounded domain with boundary ГеC2 , p = n/p is kinematic viscosity coefficient. Densi- ty p, dynamic viscosity p and characteristic relaxation time т are positive constants. Vector field f = f (x,t) determines the mass density of external forces. The system (1) is closed with respect to the unknown functions, i. e. the velocity vector u = u (x,t) and the pressure p = p (x,t). Symbols div and V denote the divergence and gradient, respectively.

We look for a solution to the system (1) satisfying the following initial and boundary conditions and the normalization condition:

u |_r = 0, w v| _r = 0, u_t =₀ = u ₀ ( x ), j p ( t , x ) dx = 0,                           (2)

G where ν is the unit vector of the outward normal to Γ .

The system (1) in a more general form was derived in [1, 2] by averaging the known kinetic model. The first variants of the system are called the system of quasigasodynamic equations. The derivation of the system and some results can be found in the monographs [3, 4]. Later, using a more general equation of state, another model known as quasihydrodynamic system of equations was developed in [5, 6]. In particular, a detailed analysis of the properties of this model is presented in the monograph [7]. Here, for a quasihydrodynamic system of equations in the case of a weakly compressible fluid (i.e., for system (1)), dissipative properties are investigated and a theorem of uniqueness of the classical solution to the main initial-boundary value problem is proven. Zlotnik A.A. in [8] constructed a system with a general regularizing velocity on the basis of a linearized (on a constant solution) quasihydrodynamic system of equations and established the degeneration of the parabolicity property of the original system. Later, for the first time, he constructed a quasigasodynamic type regularization of the heterogeneous model (in the quasihomogeneous form), for which the difference scheme an explicit two-layer in time and symmetric three-point in space in the 1D case was constructed [9]. In [10], a model based on quasigasodynamic and quasihydrodynamic equations in multiscale media is investigated, which can be used in applications to porous media theory. A computational multiscale method based on the idea of bond energy minimization was proposed to solve quasigasodynamics problems and improve the accuracy of simulations. Recently, regularized hydrodynamic equations of quasihydrodynamic type have been used in the numerical solution of a number of practical problems. Relevant results are exposed in [11–14]. Note that the system (1) is an elliptic-parabolic system and both equations, elliptic and parabolic, contain the senior derivatives of the unknown pressures p and the velocity vector u . Such systems often arise in applications. In [15], to solve the problem of two-phase non-isothermal filtration, the authors consider a system consisting of one elliptic and two parabolic equations with known boundary conditions. The authors in [16], using the technique of Fourier multipliers, proved an a priori estimate for strong solutions to elliptic-parabolic equations of mixed type in Sobolev space. In [17], a family of models for the flow and transport of multiscale single-phase fluid in inhomogeneous porous media based on an elliptic-parabolic system consisting of an elliptic equation for steady-state flow and a parabolic equation for transient advection-diffusion is described. The existence and uniqueness theorems of generalized and regular solutions of an analog of the first initial boundary value problem for the system (1) are presented in [18, 19], respectively. The proof of the existence of generalized solution in [18] is based on the Galerkin method and a priori estimates. In [19], under certain conditions on the data, it is shown that there exists a unique regular solution of the initial-boundary value problem locally in time. The existence and uniqueness theorems for generalized and regular solutions to an initial-boundary value problems for a quasihydrodynamic system in the linearized case are presented in [20]. In the case of a regular solution, there are some restrictions on the norms of the data. The obtained results provide appropriate stability estimates for solutions to the original nonlinear problem.

In this paper we study the solvability of initial-boundary value problems for the system (1) in some weight classes characterizing the behavior of generalized solutions as t ^^ .

Preliminaries

Let u,p be a sufficiently smooth solution to the problem (1), (2). We say that ue L_2loc ( 0, ж ; E ) ( E is a Banach space), if ue L ₂ ( 0, T ; E ) for any T < ж . Let щ ( t ) be a non-negative function such that

^ ( { t : w ( t ) = 0} ) = 0. Here p is the Lebesgue measure. By L 2 _W ( 0, ж ; E ) , we mean the space of measurable functions u ( t ) such that ^u e L₂ ( 0, ж ; E ) . Let us multiply the first and second equation of the system by the functions ф and W respectively such that ^e L₂ ( 0, ж ; W 1 ( G ) ) , J ^ ( x ) dx = 0, G

W e L ₂ ( 0, ж ; W 2 ( G ) ) , W| S = 0 , ^ and W have bounded supports. Integrating the results over G , we arrive at the equalities:

G       G                      ^P

p ( u, div W) + ((u, V) w, W) + (w divu, W), where the point • means the scalar product in R3 and (u,v) = juvdx for scalar functions and

G

( u,v ) = j u • vdx for vector functions. Integrating by parts, we have

G

GG

Using this equality in (3), we obtain the equations

G

(d u _!                         1

valid for almost all t . Equalities (5) can serve as a basis for defining a generalized solution to the problem. Let po e [1,3/2], qo = 2po/(4po — 3), p1 = 5/4. Then qo e[1,2]. Functions u eL2,юс(o,да; W1 (G))nLда,(o,да;L (G)), ut eLp,ioC(o,да; Wp1 (G)), p e Lp (o,да; W^ (G)) such that —+■ + (u, V)u e L2 ioc (o, да,L2 (G)), satisfying (2) are called generalized solutions of the problem (1), (2) if да

да

(u,V^)dt = (w,V^)dt, \ (—,^)—((u — w,V)^,u +—(Vp,^) + o            o            o L dt                     P да

о for all functions ^e L2 (o, да; W^ (G)) with j ф( t, x) dx = o,^ e L5 (o, да; W5 (G)) and ^s = o , having a bounded support in t . Let

a

—

The main results

Let's introduce an auxiliary weight function. We consider several different cases. In the former case в ( t ) = e ^Y ( y ^ 0, Y < № /2 S _o ) , where 5 _o is the constant ^ o from Poincare's inequality

G

G

valid for all u e W ^ ( G ) , such that u | = o . In the second case в ( t ) = ( M + 1 ) ^Y ( / ^ o ) , where M >  o is some constant, which will be chosen below.

Theorem. Let f Jft e L2 (Q) , uo e L2 (G) . Then there exists a generalized solution of the problem (1),   (2) such that   ^u eL2(o,да;W^ (G)) ,   ^u eLда(o,да;L2 (G)),   в(u,V)u eL2 (Q), в I ^p + ( u, V) u |e L2 (Q ),

^e ( ^u , ^V ) ^{u e} L_q^ ( ^o , ^да ; ^Lp_o ( ^G ) )       for      any       p ₀ ^e [ ^1,3/2 ] ,

Vpвa e La (о, да; L„ t f        qo\  ,      po

(G)), utpa e Lqo (o, да; W-^ (G)) for any po e[1,3/2] and for all a such that a < 12 if в = eY (y > 0) and a

<¹ —²— q L if e= ( t + M ) ^Y , в <  o; the case of a =¹ is possible 2  2| в | q o                                           2

1     2 — q.

^o           2  2| в | qo                                                          ^{V 7}

Proof. First, we derive the first a priori estimate with weight β for smooth solutions to the problem. Take ^ = p в , у = ви in the definition of a generalized solution. We obtain the equalities

Dividing the first equality in (6) by ρ and adding it to the second equality and using the equality

• - w, V ) u, u ) = 0, we obtain that

• £ J l u y dx - _j l u y dx + ^ (V u , V u 0) + У div u ,div u 0) + T (V p , 0 V p ) +

• ^{d t} G  ²      G ²                                    P

• — ( ( u , V ) u , 0 V p ) - — ( f , 0 V p ) -— ( u , 0V p ) + — ( v p , u 0 ) + т ( ( u , V ) u , ( u , V ) u 0 ) +

Transforming this equality, we conclude that

£ _j (I ^{u 1 0 )} dx - J ^{(| u} I ^{0 t} ) dx + p ( V и, V ив ) + p ( div u, div ив ) +

• ^{d t} G   ²       G    ²

• ₇ (^V p ^V..,. . ( ( u . ^V ) u . ( u ^{, V} )     +- ( (.V) ^{u , V} p . ⁰ ) ^-

• ρ

— j | u | ⁰ dx - j ¹ u ^{1 0 t} dx + p ( V и, V ив ) + p ( div и, div ив ) +

dt G  2      G 2

= т f f , 5

I p

Estimate the right-hand side using the Cauchy inequality

| ab | <  ⁸ a ² + ^ b ², ( 8 >  0 ) .

We have that

^{1 f 1 0} dx + -[ | ^V p + ( и , V ) и |² 0 dx

2       2^J G p

T ( f , ^V p 0 + ( и , V ) и 0 ) < A p ^G

|(f, u0)| < | j I u |2 0dx + j I f I2 0dx;1. 2 G         G

Using these inequalities in (9), we obtain

• — j ^| u ^{| 0} dx - j ^| u ^{| 0 t} dx + p ( V u , V u 0 ) + p ( div u ,div u 0 ) +

dt G  2

-1 0 | ^V p + ( u , V ) u | , I ^V p + ( u , V ) u ||< - J| f |² 0 dx + — J| f |² 0 dx + ^ -p V u |² 0 dx.

• 2 ll P        Л P        J J 2 G        28 G

  
  

Let's take 8 = ^^ ₀ . We conclude that

• — J — dx -^^x - J —— ~dx + ^— ( ^ u , V U Z ) + — ( div u , div и в ) +

^{d t} G  ²       G ^{2       2}

T

e^ p + ( U , v ) и ¹ , ^{fV p} + ( и , V ) и ¹¹<  f| 7 e x ^f - + — 1 .

Il p ^v Л p    4) G     1 ^{2 2} ^ J

Consider    the    following    two    cases:

a)      0 t <  0,    b)     Д >  0.     Let

J = —V u , V u — + — (div u ,div ив) + ^— в —^P + ( u , V uu ,| ^P + + uu ,V) w | . Integrating (14) from 0 to 4^х                  "2 VI P       JV P       J)

t , in case a) we obtain

J 1 « Ш _dx + J J Jdxdt <  C 1 J J 1 7 fp_dxdt + _J u ⁰- e ( 0) dx = M .

G    2 0 G          0 G            G 2

In the case b), we can rewrite the inequality (14) in the form

d _f। и |² e ( t ),_+fl)7. dx + | и | d t J     2          J^{1   1}

GG

1 2 1 —e 1 4 ^ 0

—

e t 1

+ Jdx <  f| /—Mx I ^— + 4 I .

¹         V 2 2 — )

Let /(t) = eY  (y > 0). Since / < — /250 , (16) implies that the inequality (15) holds. Let в = (t + M) Y (y < 0). In this case, choosing a sufficiently large number of M (—— + — > 0), we ob'    '                                                   250  M tain the inequality ^^ — — > 0 which validates the inequality (15). The inequality (15) yields 450   2

max t J

G

G

M

W) ’

f ^— ( V и , V и в) + — (div и )² в + ^— ( в ( — + ( и • V ) u ), ( ^{V p} + ( u , V ) и )) <  M .

_Q 42 pp

As a consequence, we obtain the following a priori estimates for solutions:

II “ ^1 L ( 0, » ; W 2 ( G ) ) ⁺l Idiv u 'PI L ( Q ) ⁺

^{V p} Т ё + ( u , v ) и в p

< C i ( M ) • L2 ( Q )

where C 1 ( M ) is some constant depending on M,^,r ,

II u Я Ц 0, « ; L 2 ( G ) ) < ^C ' ( M ) .

Next, we evaluate all summands included in the definition of a generalized solution. Demonstrate that

II в ⁽ "' • ^V ) u k, ,( 0, « ; L ,„ ( G )) < ^C • p » ' [ ^|,3/2 ] •                           ^(2I)

where the constant C has the same properties as the constant C ₁ . The Hölder inequality yields

II ^{в (}“•^V) “ 1,„. G . <  C lHP'² L ,g , 'И 21V,( G , •                   22

where q =----- . Next, we use the embedding W ⁵ ( G ) c L  ( G ) for p^q = r =----- , in this case

2 — p ₀                                       q ^{0 p}         -     з — 2 ^

=    ³    = 5 = ^{3 ( P} 0 ^— 1 ) .

• ^{2 —} P 0   ^{3 — 2 5}        P 0

The necessary inequality s <  1 is equivalent to the inequality p ₀ <  3/2. From (22) it follows that

II ^в » ^и ^) P I^ G ) <  C lin¹'²! L G       l, G ) .                    <²³’

We estimate the last multiplier using the interpolation inequality [21]

UeWWs(G,

where s = 0 . From (23) we obtain the estimate

II ■       < G) < ClM+’,G JIM (G ,■

Using (20), we obtain

I ^(u V) ul^ ,0^ L„ g ,, * Cl ( MXjl вСS’dt 1"’" ^ C2* MI(2

where we choose qo(1+ s) = 2>i-e- qo = 2Pol(4po-3).

By definition, q₀ > 1. The estimate (19) yields

^Vp p

4p+4fi (u^-V) u

< C ( M ).

^L2 (Q)

T       ,Vp _ ,                 „

Let g = (--+(u, V)u). Next, we infer

P

в p

Lqo*⁰^ ^LP0* G ’)

< e^ag             + \/3^a (U, V)U             .

II       II Lq₀(0,^, Lp₀( G))   II '      ⁷  1%(0,о>; Lp₀( G))

Let в > 0 and let a< 1. In this case

II e^a (u, V) ull               <| в (u, V) ull ,       ,   < C(M).

r ( ’ ) 1^(0,»;Lp0(G)) II7 ' ’ ) Up0-';LP0*G))

If A< 0 and a > 1 then similarly we have that

Iв (и- V)u||             <1 в(u- V)ull _{/A T},< C(М).

r ( ’ ) 1^(0-»; Lp0( G)) II71 ’ ) l|Lqo(0-»; Lpo*G))

Next, we derive that

»

I eg\L  (0      (G,, < (1 (llg|po dx) q0 po в   dt)’ q0

qov ’  ’o where

(11 g l^podx)q^po< (Jl g l²dx)q⁰'²co- Co = p(G)q^{o(1 po-12)}-GG

with μ is the Lebesgue measure. In this case, we infer

»

||0^яg\           < c(f(f| g |²dxУ вeq

^{11    s} IILqo(O^;Lpo(G))     ¹ J J,

_ qo   —     “            1 » М_(а -1)

^{- 2}dt) ^qo< C1( J в J l g |²dxdt )²( J e^2-qo

^2-qo

1        2 qo dt)    - (34)

0 G

Let в = eY - y > 0. In this case, for convergence of the last integral, it is necessary that a < 1l2. If в =(t+M) Y - Y < 0, then it is necessary that a <1 -(B-qo) 2   2| y | qo

.

Note that the inequality a > 0 is satisfied under the condition that 2/(1+1 y |)< q0 < 2 . Let в = eY - y < 0. For convergence of the integral, it is necessary that a > 1l2. If ft =(t+M) Y - y > 0, it is necessary that a >(2  qo ) +1

2|Y | qo   2

Note that the inequality  ---^^ + — > 1 is fulfilled whenever if —2-, > qo. if A > 0, then the ine-

21 Y1 qo   2                                      1+1 YI qualities (29), (30) imply the estimate

Il ppa\             < C (M),(37)

II Lq0(0<4Lm( G))

where a < 1/2 if в = eY (y > 0) and a <1 —2 -q0 if e=t+M)—Y,Y > 0 • The case a =1 is pos-2  2|y|q0                                          2

sible when q0 = 2. If pt < 0, the inequalities (29), (31) yield where  a > — + ——q0- and a > 1. If

²²¹y¹q0

We have obtained the estimate

II ■pll

< C (M),

II L_?0(0,®; Lp₀( G))      ^{V 7}

²   .       J       . I     •                 1 .   ^{2 — q}Cl

----->q₀  then the inequality  — +----— ¹⁺\ Y^{1                                        2   2}\ Y^{1 q}0

holds.

¹ L_?0<0’”; Lp0( G))

ILq0(0,«;L„(G» < ^C4 I">•

As a consequence, if p₀ = p1 = 5/4 (p₀ = q₀in this case) then we conclude that

II^PVpL (Q) ⁺lH^U-^VH,,.Q) < ^C4 ⁽M )■ p1                       ^p1

Since

- I Vp w = т —

we have the following inequality for the norm of w :

II^l-Q) < в(Vp

+ (и, V) и

²L2( Q )

II ^p  fl (Q) < C5 ⁽“ ) ■

Let us estimate the summands from the definition of a generalized solution. We have that

—

^w, ^V)v,u) = j^( и^—w ) уjx, ujdx.

G ,j

Consider the functional l(^). The Holder inequality yields

I = 1 wwxUjdx,\I¹<|ML (G)'IML ,_(G д/^p0■1/^p0=¹

G                              ^p0              p0^{y J}

Further, we obtain (see (20)) that

_1_

[J|H.,|«(Uj)p⁰dx]- <|W;|L(G)

G

C₆||w|| m' и *  <1 WiLn

6 11 4IL2( G) 11 J\\ws_(G)    ii ^;hl₂( g )

where s = 3 (p0 — 1)/p0 . We can conclude that да

'Ikl<

^{11 j||}L 2p0 ^,"'^/'Lq0(^G))

^2—p0

Iи Is     '|U |1_s=

II jUw^G) 11 jllL2( G)

^

iimi I0.) <i pq 1 h; ( g )i hUg )i ы Hl dt< cill м^с. ,11 >-H)

dt,

where C = II pku\         ■ Applying the Holder inequality with q = —, we infer

⁷¹¹L^ (0,^; L2( G))                                                               q₀

II^pI^L  (0,«)

^q0

® i q0        г г

2      ^2—q0

0^2—q0dt ]^{2 q0}■

¹ W2( G)

2sq^

Note that —— = 2. In this case the previous inequality can be rewritten as

IIвМL,  IM S (M)■

^q0

The expression

l(^)=E j wijudx=((w. V)^. u)

• i . j G

is a linear continuous functional over W p‘ (G). It follows from (44), (47) that

• 11    (iW-;(G) =      ■               SC>lwit2(g)-lКJ(G)-I •    ((G)■

HgW^. (G) нW 0(GI'

where p‘ = p₀/ (p₀ -1). Using (48), we obtain that

IIlИ1 ,»„»-1(G)) S C  (M )■(51)

qov ’

Denote

(Vp.i) = li(i). Vp g Lqo (0,ад;Lp^ (G)).(52)

This expression has a sense for functions i g Lq‘ (0. ад; Lp‘ (G)) with a bounded support. Then we have l1(i) S||VpWl^ (G) * IH Llpb (G )■

In view of the estimates (37), (38), we derive

II liel m HoS KVp|l      (C Cii (M) ■(54)

^Lq₀⁽⁰.™^W_PO^(G))   ^{11         llL}q₀^(0,№; ^Lp₀^(G))

For integrals of the form

12(H) = (( u. V)H. u ) = E j uiijxUjdxdt. l₃(H) = (( u. V)H. w).

• i.    j G

we have the estimates (as in the proof of the estimate (53))

11НИL ,0 GW-) S C12 (M).‘ = 2,3.(55)

• q0v .

Let {^i} - be a basis for the subspace of the space W^( G), consisting of functions ^, satisfying the condition j ^dx = 0 . As vector functions {Hi}, we choose the eigenfunctions of the problem

G

-AH = Ah. Hr= 0. H = (iiH2H3)gW2(G)^w2(G).(56)

PN g L(V.V) and, in view of duality and selfadjointness, it allows an extension to a bounded operator of the class L(v .V ), where V - dual space constructed by L2(G) and V as a completion of L2(G) with respect to the norm ||u||r' = sup | {u,v)V | /||v||  . In particular, we have that (u.PNv) = (PNu.v) for all v∈V v g V. u g V . Note that W2(G) n W2(G) c W 5(G) and the embedding is dense. This is a consequence of the embedding theorems. Since V c W 5(G), we have that W5- 14 (G) c V . Let Xi be the corresponding eigenvalues.

We look for an approximate solution to the problem in the form

NN un=E ci (t )Hi (x). pn=Ea (t )^i (x) ■ i=1                              i=1

where ci (t) and ai (t) are solutions to the system:

( uN - wN, V9j ) = 0, a ( uN Wj ) = ( fWj ), ci( 0 ) = ( u0Wi), j = I,--, N •

The first equation of the system can be rewritten as uN - -ppN--T (uN V) uN + fT, V^;| = 0-(58)

PJ

We have that

N

—, V^ | = - X«j (t )(V?J, V^i) ,det (V^j, V^)/ 0-(59)

P      J  P j=i

The last determinant is the Gram determinant and it does not vanish. Indeed, the following estimate holds:

II^VpWl, (G) - c0 IpL (G) ^VP^{e W (G}) ^:J Pdx = ⁰-G

This inequality guarantees that an equivalent inner product (u,v) = (Vu,Vv) can be introduced in the required subspace of functions 9, which guarantees the claim. Let A be a matrix with elements aij = (V9, V 9- ). In this case the system (58) is rewritten in the form a = P A1 la        -^A

T

7^uN^-T(^uN,^V)^uN^{+ Tf} ,91) '

Jun-t ( un , V) un + Tf ,9n ^

Substituting a into the second system, we obtain a nonlinear system of ordinary differential equa tions for functions ci (t). The a priori estimate below guarantees that the Cauchy problem for this sys tem has a solution on the entire interval (0, ^).

Further, we obtain a priori estimates for approximate solutions. Multiply the first and the second equation of the system (57) by ai and ci , respectively, and summarize the equalities over i. Then we obtain that

(^uN^-wN,^VPN ) = ⁰, a (^uN,^uN ) = (^f, ^uN )^{- (61)}

We have the above-proven estimates (19), (20) and, thus,

||^uN ^1 Il₂ (0,«;W₂¹(G)) +1 l^{div u}N ^в\L₂(Q) ⁺

(VPN l P

- Ci (M) -

L2( Q)

where C₁(M) is some constant depending on M, p,r, I^uN^1 l^g» ⁵CKM)-                    ⁽⁶³⁾

The estimate has the same form because PPNfLL2(G) 51|fIL(G) ,  IML(G) -Ilu0lIL(G) , uN(0,x) = PNu0 . Take p0 = q0 = 5/4 and fix the parameter a = a0 , satisfying the conditions from the statement of the theorem. As a consequence of (26), (28), (40), (42), we infer

II wN ^11 L^Q, ⁺|^VPN ■'  L,., Q, +K ^uN'^V)uN^в  .     ^C4 ⁽M )-

Obtain an estimate for the derivative with respect to time of a solution. To this end, we rewrite the second equation of the system in the form

PuN Wl = ((un - Wn,V)^,un)--(VPn,W) + l dt    J                        P

p(Vu_N, VW)-a( div u_N ,divW)-((u_N, V)W, wn) + (f W) = L0W),            (65)

where W G VN . It is easy to see that the expression L0(W) is a linear continuous functional over the space W 5(G) in view of the estimates (53), (54), (55) (where the u is used instead of uN ) and thereby also over the space V. Hence, there is gN (t) e V such that L0(V) = (gN ,V) for all V e V• The estimates (34), (53), (54), (55), (61)–(64) ensure that

II gN в“°|          <1 U в"⁰!!         ,    < C12 (M),                 (66)

II           II L5/4(0,®;V')    II           IIL₅/4(0,®;»5-4( G))

where C12 - some constant depending on M and independent of N. The equality (65) can be rewritten in the form uNt = PNgN .

The previous estimates and boundedness of the operator P_N in V^' imply that

Iив\       , <C12(M),                          (67)

l_5/4(0,^;V ‘)

The sequence u_N is bounded in space endowed with the norm

I= 1   \^G G» +lk°l^даИ              ⁽⁶⁸⁾

and the estimates (62)–(64) are valid. Hence, there exists a subsequence uN   and function il e L2 ^(0,®; W21(G)) such that uN^ ^P ^ujfi in L2(0,«; W^(G)) weakly, uNkx. в^^ ux 4в weakly in L2 (Q), uNt ^ ut weakly in L5/4(0, да; V), div UN в^ ^ div й^в weakly in L2 (Q),

WN в ^ uд/в weakly in L2 (Q), p. в“0 ^ рв*0 weakly in L5/4 (Q), в“0VPn ^ в“0VP and kkk

0(U_N ,V)u_N ^ ви weakly in L_5/4(Q), Puu_N ^ вй™ weakly in L„ (0,да;L₂(G)) . Demonstrate

Nk^   '             1                   5 4^^         Nk                               да2- that

∇p w = —+ (и,V)и — f, u1 =(и,V)и,(69)

Construct an increasing sequence Tk →∞ at k →∞ . In view of the estimate (68), the subsequence uN  is bounded in the space endowed with the norm u|| = U^Wr     wVm+lUea0||          •(70)

IIn    II IL2(0,t;;W2(G))      t^   |L5/4(0,t;V‘)

Next, we will use the compactness theorem (Theorem 5.1 of Chap. 1 in [22]). Note that the embed ding W 2( G)c L2 (G) is compact. By the compactness theorem, there exists a sequence и 1N such that и1 ^ и strongly in L2 (Qt ), QT = (0, T) x G and almost everywhere in QT . Again using the com-Nk                    2^ TUI" ^1      1/                                  T pactness theorem, from the subsequence иД we can select a subsequence un  such that UN ^ и strongly L2(QT) and almost everywhere in QT . Repeating the arguments, we construct the family of subsequences ulN such that ulN ^ и strongly L2 (QT ) and almost everywhere in QT . Now, define the

Nk             Nk                 ²Tl_t                             T^

subsequence v_k= u_N^k_k , which converges in L₂(Q^ ) to и for all i and almost everywhere in Q . Fix i and take the function V e L_да(Q) such that supp^ c Q_T. . We have

fв((vk,V)vNk -(u,V)u)^dQ = Jв(((vk— u),V)vk + (u,V)(u—vk)\vdQ. QQ

The first integral is estimated as follows:

^U),^V) vk-^dQ< ^с1з|vk

-

^u1 L2(8_S>I 'WL®,> ^^{0 atk} "

Moreover, we have that

j(u, V)(u - vk )-^dQ ^ 0 at k ^да, Q due to weak convergence of вVvk to вVu in L2 (Q). Since the convergence takes place for all i and the set of functions with a bounded support of the class Lда(Q) is dense in L2 ^ (0,^;L2(G)) , we can Vp conclude that u1 =(u, V) u and thereby w = — + (u, V) u - f . A subsequence vk coincides with some subsequence uNk for a suitable choice of the sequence Nk . Fix T > 0 and take the set of functions ai (t), ci (t) e C([0, да)), such that sup ai ,supci c[0, T], multiply the corresponding equalities (57) with N = Nk by these functions, sum the result on i from 1 to n (n < Nk ) and integrate the obtained equations on t . As a result, we have

n

да

К uNk 0

n

—

®                   да

WN_k, Vp)dt = 0, ja(uN_k ,^)dt = j(f ,^)dt, 0                   0

where ^ = ^ci^i and p = ^aipi. Let us consider successively all summands. First, we can pass to

i=1

i =1

the limit in the first equality and obtain that да                                                  i           ^

0                       \         ^       7

In the second equality, we consider only the nonlinear summands, since in the linear part the passage to the limit is realized due to the weak convergence. Consider the summand да

0 x да

Demonstrate that J_N^ ^ J = j ((u — w,V)^,u)dt as k^ да. Consider the difference

JNk

да

^—wNk , ^V)7,^uN_k

— udt + 1Цu_Nk

—

w_Nk, v)^),udt.

The second integral tends to zero due to weak convergence, and the first integral is estimated as follows:

u_Nk

^—wN_k , ^V)7,^uNk

• —    u)dt< c||;

uN_k

• —    u     ^ 0 as k ^да.

L₂( Qt )

Similarly, we can show that J ((u_Nk , ^V)7, ^wN_k )^dt ^ j((^u, ^V)7,w) dt at k ^да. Passing the limit 0                             0

as k ^ да, we can conclude that даГдU                     1                                                 7/-.\.

0 ^^dt   '                     ^P                                                            0

In view of the choice the basis, we obtain that u is a generalized solution to the problem. Proof of the last statement of the theorem, i.e., inclusions   Vp,(u, Vu)u e Lq® (0,да;LP0(G)), uea e Lqo(0, да;Wp^(G)) for any p0 e [1,3/2] and the corresponding parameters a was carried out in the first half of the proof.