Генератор монохроматических автоколебаний в дискретном времени

В автогенераторах квазигармонических колебаний (автогенераторах томсоновского типа) функцию ограничения амплитуды автоколебаний выполняет нелинейность [1; 2]. Одновременно с этим она является причиной генерации высших гармоник основной частоты, которые ухудшают динамические характеристики и снижают стабильность частоты автогенераторов. В аналоговой электронике основной способ снижения уровня гармоник – это повышение добротности колебательной системы автогенератора. Но полностью избавиться от гармонических составляющих на практике не удается.

Формулируя математические модели автогенераторов в дискретном времени, мы получаем алгоритмы генерации дискретных автоколебаний (ДВ-автоколебаний). Такие алгоритмы могут также рассматриваться как самостоятельные объекты нелинейной динамики – ДВ-генераторы. В них гармоники существенно усложняют динамику автоколебаний, в частности, приводят к возникновению эффектов, не характерных для аналоговых систем [3; 4]. Поиск возможностей для повышения спектральной чистоты ДВ-автоколебаний в таком случае представляет значительный интерес.

В настоящей статье в рассмотрение вводится томсоновский ДВ-генератор с кубической нелинейностью, имеющий в режиме свободных автоколебаний спектр без гармонических составля- ющих. Синтез проведен методом инвариантности импульсных характеристик [5] на основе гармонически линеаризованного аналогового прототипа.

1. Томсоновский автогенератор в непрерывном времени

В качестве исходной модели автогенератора томсоновского типа примем модель с кубической нелинейностью, определяемую уравнением движения вида d2 x to, dx 9       to  d (    1

+ 0    + ton x = p 0 I x - x I dt2 Q dt             Q dt I 3   J,       (1)

где tog и Q — собственная частота и добротность линейного резонатора; p – параметр превыше ния порога генерации (порог: p = 1).

В теории колебаний широко известен метод гармонической линеаризации [6]. Он заключается в замене нелинейных слагаемых в уравнении движения системы формально линейными, но зависящими от амплитуды колебаний в предполагаемом решении. По отношению к уравнению (1) эта процедура выглядит следующим образом.

Для решения

x ( t ) = a cos(to g t ) = a cos V разложение функции

G (x) = x x в правой части (1) в ряд Фурье имеет вид

G ( a cos w ) = 1 - — a ² a cos w—— a 3 cos3w.

v            ^    4 j           12

Это выражение заменяется приближенным

G (a cos w) = ^1 - ^a2 j a cos W = S(a2)x и используется в правой части (1). В результате получается линеаризованное уравнение d2 x to, dx            to

—- + 0 —+to2 x = p 0 S (a2)—.(2)

dt2   Qdt   0 Qdt

Заметим также, что помимо обнуления высших гармоник, генерируемых нелинейностью, в рамках метода учитывается медленность амплитуды a ( t ). Поэтому в правой части уравнения (2) амплитуда не дифференцируется.

Предполагая в дальнейшем дискретизацию времени с интервалом А, введем в уравнение (2) безразмерную временную переменную т = t / А: d ² x     dx 22          2 dx

—— + 2nv— + 4n²Q 2 x = 2nv pS ( a ²) —.      (3)

d т²        d т                        d т

Здесь Q g = to g / to d — собственная частота, измеряемая в единицах частоты дискретизации to d = 2п / А; v = Q g / Q — полоса резонатора.

• 2.    Автогенератор в дискретном времени

Метод инвариантности импульсных характеристик широко применяется при синтезе дискретных линейных фильтров по аналоговым моделям-прототипам. Он основан на использовании последовательности временных отсчетов импульсной характеристики прототипа в качестве импульсной характеристики ДВ-фильтра. В работе [7] метод предложено применять для нелинейных систем.

В рассматриваемой ситуации правую часть уравнения (3) формально предлагается считать внешним воздействием линейный резонатор таким, что импульсная характеристика определяется уравнением d-h + 2nv — + 4n2Q2 h = 4л2Q25(т).

d т² d т

Последовательность отсчетов h [ n ] = h (т _n ) на временной сетке т _n = n формирует импульсную характеристику линеаризованной ДВ-системы с прототипом (3):

h [ n ] = 2nQ g exp ( -nv n ) sin(2nQ g n ), n = 0,1,2,...

Дискретное преобразование Фурье последовательности (4) дает частотную характеристику, которая, в свою очередь, позволяет представить ДВ-генератор в форме рекурсивной системы второго порядка:

x[n] - 2a cos (2nQg) x[n -1] + a2x[n - 2] = = 2navpsinc (2nQg) S(a2[n - 1])x[n - 1], где sinc (2nQg) — кардинальный синус; a = = exp(-nv) — параметр диссипативности.

Разностное уравнение (5) содержит производную x[n] = (dx / dт)т=n . Для ее определения воспользуемся выражением sinc (2nQg) x[n] = cos (2nQg) x[n] - x[n - 1]. (6) Оно является точным для гармонических колебаний с частотой Qg, а для квазигармониче- ских – может рассматриваться как гармоническая аппроксимация скорости. Выражение (6) и справедливое для гармонических колебаний ра- венство w [ n ] = a 2[ n ] = x 2[ n ] +--- x [ n ] 4n2Qg позволяют также вычислять мощность w[n] по мгновенным значениям осцилляций:

w [ n ] =---2------- x sin2 (2nQg)

x ( x ²[ n ] - 2 cos ( 2nQ g ) x [ n ] x [ n - 1] + x ²[ n - 1] ) .

Эта мощность – аргумент функции S ( a ²) в уравнении (5):

S ( w ) = 1 - — w .

Таким образом, с учетом выражений (6) и (7) уравнение движения ДВ-генератора (5) приобретает вид

x [ n ] - 2a cos ( 2nQg ) x [ n -1] + a² x [ n - 2] =

= у S (w[n - 1]) (cos (2nQg) x[n - 1] - x[n - 2]), где у = 2navp — параметр глубины обратной связи.

Отметим, что лишь одно из двух выражений (7) и (8), описывающих ДВ-генератор, является уравнением динамической системы второго порядка – уравнение (8). Второе – уравнение (7) описывает безынерционное нелинейное преобразование. Поэтому в целом порядок динамической системы (7)–(8) равен двум.

• 3.    Численный эксперимент с ДВ-генератором

Последовательность шагов синтеза ДВ-гене-ратора (8) позволяет предполагать, что при совпадении частоты генерации Q _a с собственной

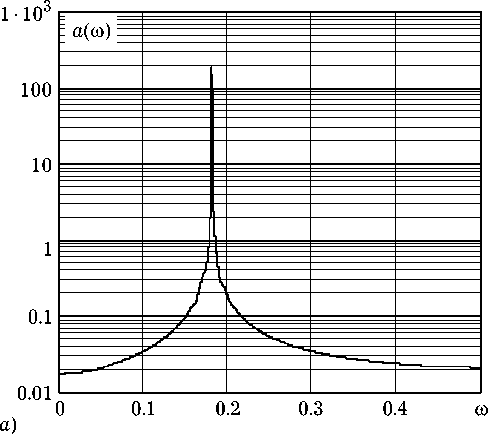
Рис. 1. Амплитудные спектры автоколебаний в ДВ-генераторах (8) и (9)

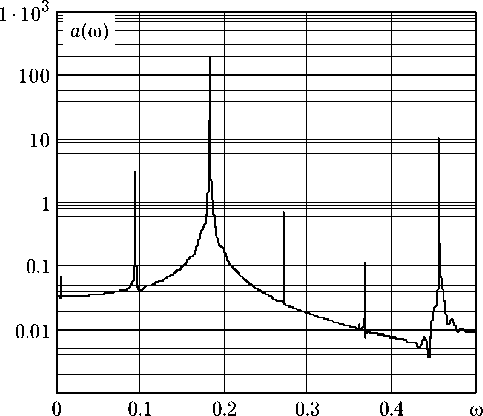
частотой Q o его автоколебания не содержат гармоник. Численный эксперимент подтверждает справедливость предположения. Действительно, на рис. 1, а приведен амплитудный спектр автоколебаний в ДВ-генераторе с параметрами Q o = 0.18, Q = 30 и p = 5 (у = 0.185). Оценка спектра проведена дискретным преобразованием Фурье временного ряда x [ n ] длиной N = 16384. Для сравнения на рис. 1, б показан аналогичный спектр для ДВ-осциллятора Ван дер Поля [7]:

x [ n ] - 2а cos ( 2nQ 0 ) x [ n - 1] + a² x [ n - 2] =

= y(1 - x2[n - 1]) x (9)

x ( cos ( 2nQ 0 ) x [ n - 1] - x [ n - 2] ) .

Отсутствие гармонических составляющих спектра хорошо видно на рис. 1, а , в то время как, рис. 1, б демонстрирует спектр, обогащенный гармониками, в том числе подмененными.

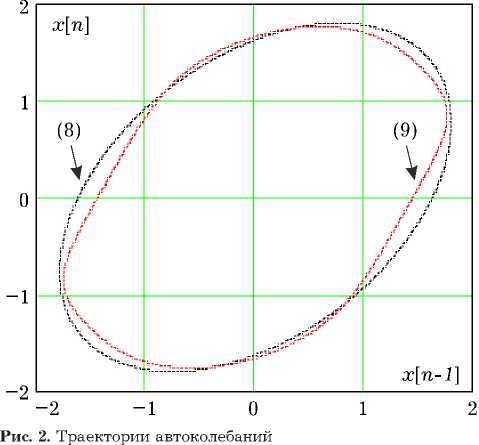
Влияние гармоник основной частоты на форму сигнала позволяет оценить рис. 2, на котором показаны траектории автоколебаний на фазовой плоскости ( x [ n - 1], x [ n ] ) . Кривая (8) — эллипс.

Заключение

Предложенный метод синтеза ДВ-генераторов со строго гармоническими автоколебаниями не связан с моделью кубической нелинейности системы-прототипа. Крутизна S ( a ²) в уравнении (2) должна лишь допускать наличие стационарного режима автоколебаний. Основным положением является аппроксимация (6) скорости осцилляций и основанная на ней оценка (7) амплитуды (мгновенной мощности) автоколебаний.

Синтезируемые предложенным способом ДВ-генераторы можно использовать в качестве нелинейных функциональных узлов в численных моделях сложных радиоэлектронных устройств. Кроме того, они могут служить основой алгоритмов обработки дискретных (цифровых) сигналов.