Генетические коды некоторых групп малого ранга
Автор: Созутов Анатолий Ильич, Синицин Владимир Михайлович
Журнал: Вестник Красноярского государственного педагогического университета им. В.П. Астафьева @vestnik-kspu
Рубрика: Информационные технологии в математике
Статья в выпуске: 1 (23), 2013 года.
Бесплатный доступ
Статья посвящена исследованию групп Коксетера рангов ? 5 с порождающим множеством S, порядки попарных произведений из которого не превышают 3, а также поиску естественных дополнительных соотношений, при которых данные группы конечны. В исследовании применяются ЭВМ и специализированное программное обеспечение «Magma». В работе найдены определяющие соотношения конечных групп, связанных с группами малых рангов ? 5, порожденных 3-транспозициями.
Порождающие элементы, конечные группы, граф группы коксетера, инволюции
Короткий адрес: https://sciup.org/144153663
IDR: 144153663
Текст научной статьи Генетические коды некоторых групп малого ранга
О
дним из важных направлений в теории групп является исследование групп, за- данных порождающими элементами и соотношениями. Данные группы возникают естественным образом во многих областях математики и связанных с нею дисциплин, особенно в некоторых разделах кристаллографии, геометрии и топологии. Однако такое задание группы имеет ряд сложностей, связанных с определением её строения и свойств.
Объектом исследования в данной работе являются группы малых рангов, порожденные инволюциями, в том числе группы с 3-транспозициями. Цель исследования – нахождение соотношений, при которых рассматриваемые группы конечны. Вычисления проводятся по алгоритму Тодда – Коксетера с помощью программного обеспечения Magma .
1. Напомним, что множество D = aG инволюций группы G называется классом 3-транспозиций , если l ab l ≤ 3 для любых a, b D и G = D
[ Fischer, с. 8]. Наиболее известными примерами групп с 3-транспозициями являются симметрические группы Sn всех перестановок степени n с классом D обычных транспозиций, которые переставляют (меняют местами) ровно две точ-
Generators, finite groups, Coxeter count groups, involution.
The article is devoted to the Coxeter groups of ranks ≤ 5 with generating set S, whose orders of pairwise products do not exceed 3, and to the search for natural additional relationships in which these groups are finite.
A computer and specialized software “Magma” were used in the study. In the paper we present the defining relations of finite groups connected with the groups of low ranks ≤ 5 generated by 3-transpositions.
ВЕСТНИК
ки (символа), а остальные n – 2 точки (символа) оставляют неподвижными. Класс D 3-транспозиций в симметрической группе Sn определен однозначно, за исключением случая n = 6, когда в группе два класса 3-транспозиций.
В данной работе группа порождается множеством X элементов порядка 2 (инволюций) и l xy l ≤ 3 для x, y X . Поставим множеству X в соответствие граф Г( X) , строящийся аналогично графу группы Коксетера [Бурбаки, 1972, с. 120]: 1) вершинами графа Г( X ) являются элементы из X ; 2) вершины a, b соединены ребром в Г( X) в том и только том случае, когда инволюции a и b неперестановочны и l ab l = 3 . Если X – минимальная система порождающих группы W , граф Г = Г( X) называем графом группы W , число l X l – рангом группы W .
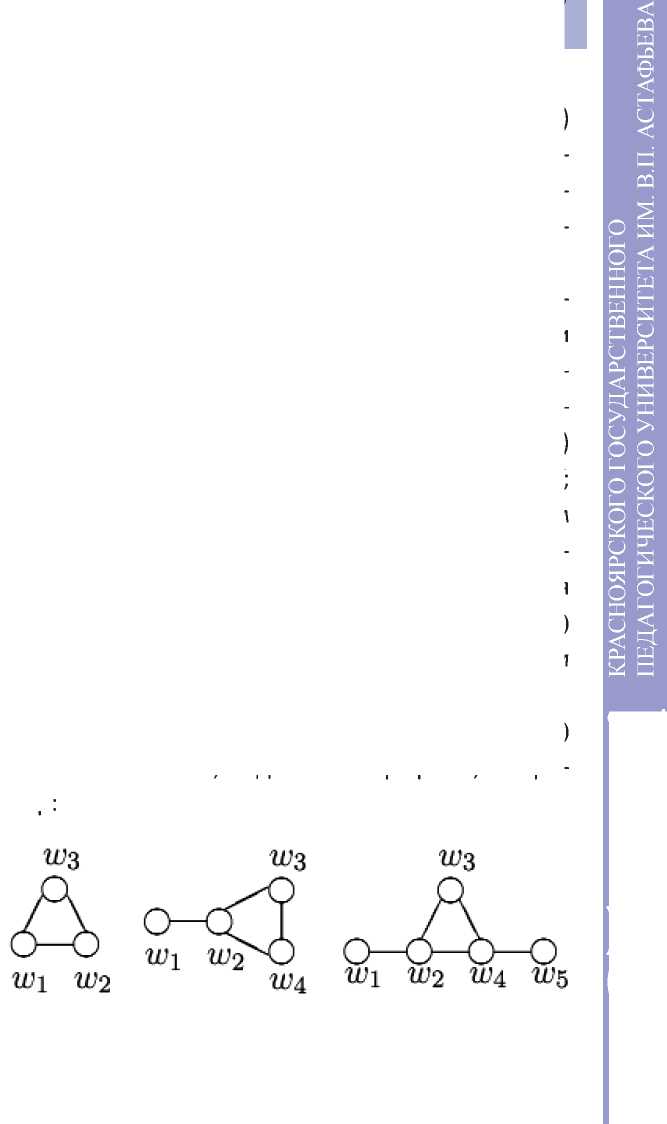
Рассмотрим группы W = W ir ... w n> ( n = 3,4,5) с соотношениями, заданными графами, например:
Известно, что эти группы и группы с графом, содержащим цикл, бесконечны (табл.). Обозначим через G(p) группу, полученную из группы W наложением дополнительного соотношения v p = 1.
Таблица
|
Граф группы G |
Дополнительные соотношения v p = 1 |
Порядок группы Gp |
|
Нет |
00 |
|
|
( wiw2w 3 ) ) 2 = 1 |
2 . 32 |
|
|
W3 |
( WjWW ) 3 = 1 |
1 |
|
( W1W 2 W3 ) 5 = 1 |
1 |
|
|
W1 W2 |
( wiw2wiw3 ) 2 = 1 |
23 . 3 |
|
( wiw2wiw3 ) 3 = 1 |
2 . 33 |
|
|
( W1W 2 W1W 3 ) 5 = 1 |
2 . 3 . 52 |
|
|
Нет |
00 |
|
|
W3 |
( w3w2w4 )2 = 1 |
23 . 3 |
|
( w3w2w3w4 ) 2 = 1 |
23 . 3 . 5 |
|
|
wT |
( www w4 ) 3 = 1 |
23 . 34 |
|
№4 |
||
|
( W1W 2 W4W 2 W1W3 ) 2 = 1 |
23 . 3 . 5 |
|
|
( W1W 2 W4W 2 W1W3 ) 3 = 1 |
23 . 34 |
|
|
Нет |
00 |
|
|
W4 |
( w 1w2w4w3 )2 = 1 |
25 . 3 |
|
( w 1 w 2 w 4w3 )3 = 1 |
2 . 3 |
|
|
( w 1w2w4 w 3 )5 = 1 |
2 . 3 |
|
|
W1 W2 W3 |
||
|
( w1w4w2w4w1w3 ) 2 = 1 |
26 . 3 |
|
|
( w1w4w2w4w1w3 ) 3 = 1 |
23 . 34 |
|
|
Нет |
00 |
|
|
to 4 |
( w1w2w3w4 ) 2 = 1 |
25 . 3 |
|
( w1w2w4w3 ) 2 = 1 |
23 . 3 |
|
|
W1 to2 W3 |
( w2w4w3w2w1 ) 2 = 1 |
23 . 32 |
|
( w2w4w3w2w1 ) 3 = 1 |
1 |
Продолжение табл.
|
Граф группы G |
Дополнительные соотношения v p = 1 |
Порядок группы G p |
|
W4 W3 Wi W2 |
Нет ( w1w2w3w4 ) 2 = 1 ( W 1 W 2 W 1 W 3 W 1 W 4 ) 2 = 1 ( w1w2w3w4w2w3 ) 2 = 1 |
OO 2 5 . 32 27 . 32 23 . 32 |
|
Wj W5 w2 w3 |
Нет ( W1W2W3W4W 5 . ) 2 = 1 ( w1w2w3w1w4w5 ) 2 = 1 ( W 1 W 2 W 3 W 1 W 4 W 5 ) 3 = 1 |
00 2 2 23 . 3 . 5 |
|
W4 W3 |
Нет ( w2w3w4w5 ) 2 = 1 ( w2w3w5w4 ) 2 = 1
( w2w3w4w2w5 ) 2 = 1
( w2w3w4w2w1 ) 2 = 1 |
00 23 . 3 . 5 2 27 . 3 . 5 2 23 . 3 . 5 23 . 3 . 5 23 . 3 . 5 |
|
Wo wT^to^”^^^ W4 |
Нет ( w3w4w5 ) 2 = 1 ( w4w1w3w5 ) 2 = 1 ( W2W3W5W4 ) 3 = 1 ( W2W3W5W4 ) 5 = 1 ( w4w3w4w5 ) 2 = 1 ( W4W3W4w5 ) 3 = 1 ( w2w3w5w3w2w4 ) 2 = 1 ( w2w3w5w3w2w4 ) 3 = 1 ( w1w2w3w5w3w2w1w4 ) 2 = 1 ( w1w2w3w5w3w2w1w4 ) 3 = 1 |
00 23 . 3 . 5 23 . 3 . 5 23 . 3 . 5 28 . 32 . 5 2 4 . 32 . 5 23 . 35 . 5 2 4 . 32 . 5 23 . 35 . 5 24 . 32 . 5 23 . 35 . 5 |
о о
g
о о д д
S д
с
к
к
к д
о о
к
о
с
ВЕСТНИК
Окончание табл.
|
Граф группы G |
Дополнительные соотношения v p = 1 |
Порядок группы Gp |
|
Нет |
00 |
|
|
( w2W4W 3 )2 = 1 |
23 . 3 . 5 |
|
|
W4 |
( W 1 W 2 W 4 W 1 W 3 ) 2 = 1 |
23 . 3 . 5 |
|
( W 1 W 2 W 4 W 1 W 3 ) 3 = 1 |
1 |
|
|
W1 'W^O^ W5 w3 |
( w2w4w3w5 )2 = 1 |
23 . 3 . 5 |
|
( w2w4w3w5 ) 2 = 1 |
27 . 3 . 5 |
|
|
( w3w2w3w5w3w4 ) 3 = 1 |
29 . 32 . 52 |
|
|
( w3w2w5w3w4 ) 2 = 1 |
27 . 3 . 5 |
|
|
Нет |
00 |
|
|
W3 W5 |
( w3w1w2w4w5 ) 2 = 1 |
2 . 3 |
|
( w2w4w3 ) 2 = 1 |
213 . 32 . 5 |
|
|
( w1w2w3 ) 2 = 1 |
2 . 3 |
|
|
W2 W4 |
( w2w3w5 ) 2 = 1 |
2 . 3 |
|
( w1w2w3w5w2w4 ) 2 = 1 |
23 . 3 . 5 |
|
|
Нет |
00 |
|
|
( w1w3w2w4 ) 2 = 1 |
2 |
|
|
w3 |
||
|
( w3w2w3w4 ) 2 = 1 |
2 4 . 32 . 5 |
|
|
( W 3 W 2 W 3 W 4 )3 = 1 |
27 . 3 4 . 5 |
|
|
if; if2 LT: Й |
( w3w2w1w2w3w4 ) 2 = 1 |
2 4 . 32 . 5 |
|
( w3w2w1w2w3w4 ) 3 = 1 |
27 . 3 4 . 5 |
|
|
( W 1 W 2 W 1 W 3 W 4 W 5 ) 5 = 1 |
213 . 32 . 5 |
Расчетами, проведенными на компьютере с помощью алгоритма Тодда – Коксетера, были получены дополнительные соотношения вида v p = 1 , при которых рассматриваемые группы конечны. Результаты приведены в таблице.


