Генетико-математическое моделирование взаимодействия популяций

Возникновение в мире пандемии COVID-19 поставило ряд научно-технических проблем. Это прежде всего практическая задача создания вакцины против коронавируса. Не вызывает сомнения, что эта задача будет успешно решена в ближайшее время, т. к. над созданием вакцины работают многие научные центры в развитых странах, выделяются достаточные средства для исследований.

Однако возникли и другие вопросы. В частности, представляет интерес прогноз, как долго может длиться пандемия, какие глобальные последствия возникнут из-за распространения заболевания. Не претендуя на исчерпывающие ответы на данные вопросы, заметим, что проблема определения длительности пандемии может быть частично решена на основе генетико-математического моделирования процесса взаимодействия двух популяций: человеческой и вирусной.

Прежде всего отметим, что вирусная популяция взаимодействует не с человеческой популяцией как совокупностью очень сложных организмов, а с популяцией отдельных клеток организма. Смерть человека при вирусной атаке является достаточно эксклюзивным событием, хотя именно по смертности оценивают распространение, например, коронавирусной инфекции, успешность борьбы с ней.

В реальности вирус взаимодействует с клеткой организма. В результате этого взаимодействия клетка может погибнуть, что обычно не приводит к гибели организма в целом. В процессе взаимодействия может погибнуть также и вирус вследствие функционирования иммунной системы человека, возникновения антител к вирусному антигену.

При моделировании задачи взаимодействия вируса и клетки какого-либо органа человека возникает две проблемы. Во-первых, нужно генетически обоснованно моделировать воздействие первой популяции (человеческой или, точнее, клеточной) на вторую популяцию (вирусную) и второй популяции на первую. Естественно, эти воздействия могут осуществляться по разным законам. Во-вторых, нужно учесть различный масштаб времени для обеих популяций, т. к. среднее время жизни клеток человеческих особей может существенно отличаться от среднего времени жизни вирусов. Эти факторы делают решение задачи взаимодействия популяций достаточно сложной.

• 1 . Закон Харди – Вайнберга для взаимодействующих популяций

Если имеется некоторый мутагенный фактор D ₂₁, действующий со стороны второй популяции на первую, то закон Харди – Вайнберга для первой популяции можно записать в виде [1]:

[м^^е © Волобуев А.Н. и др., 2020

d q_{f 1}

dn ₁ ²

dq_{f 1}

+ In 2—-— - D. , dn ₁       2,1 ,

Таким образом, уравнения (1) и (3) приобретают вид:

где qf 1 – частота рецессивного женского аллеля первой популяции, подвергающегося воздействию со стороны второй популяции. В качестве первой популяции мы рассматриваем клетки органа человека, например клетки печени. Безразмерное вре-t мя n^ - —, где T - среднее время жизни клеток 1 T1         1

органа для особи первой популяции. Для клеток печени по разным источникам T 1 ® 140 суток [2-4].

Закон Харди – Вайнберга для второй популяции запишем аналогично:

d ² q f          dq f

—5-⁺ln²-7— ^-ai q ₂, dn ²         dn

У ² dlql + y ln 2 dq ² ₌ „ 2 .

dn ^{2         dn}

В уравнениях (4) и (5) индекс у безразмерного времени опущен, т. к. осуществлен переход к единому безразмерному времени n - n 1 .

d - q^ + ln 2 dq ² - D

dn ₂ ²

При что во

dn 2

1,2 .

записи уравнения (2) мы предположили, второй популяции отсутствует разделение

2. Развитие вирусной популяции во время пандемии

Уравнение (5) для второй (вирусной) популяции при воздействии на нее иммунной системы первой популяции может быть решено безотносительно уравнения (4).

Интегрируем один раз уравнение (5):

на мужские и женские особи, так что q2 - частота рецессивного аллеля, который подвергается воздействию, в геноме второй популяции. Например, такая ситуация характерна для бактериальной, микробной или вирусной популяций. Безразмер-t ное время n2 - —, где Т2 - среднее время жизни 2 T2        2

особи второй популяции. Например, для вируса гриппа T 2 ® 7 суток [2-4]. Мутагенный фактор, действующий со стороны иммунной системы первой популяции на вторую, обозначен D ₁₂.

Введем единое безразмерное время. Из условия T 1

n 1 T 1 - n 2 T 2 находим n 2 - — n 1 - —n 1 , где посто- T Y

T ²

янная у- ² ~ 0,05. Следовательно, уравнение (2) T ₁

можно переписать в виде

₂ dq

Y —² + Y ln 2 q 2 -« 2 n + С , dn    ^{22  1}

где C ₁ – постоянная интегрирования.

Для решения уравнения (6) представим функцию ^ 2 в виде произведения двух функций q 2 - uv . Тогда уравнение (6) перепишется в виде

2 du 2 dv

Y v — + Y u^-;- + Y ln2 uv - a₂ n + C .

dn dn       ²¹

Группируя слагаемые, найдем:

I du      Y 2 dv

Y v I Y— + ln2 u l + Y u— - ^a 2 n + C i •

( dn        ) dn

Y ² d ^ q l + у ln2 dq ² - D. ₂.

dn ²          dn 1      ^{1 , 2}

Рассмотрим мутагенные факторы. Предположим, что аллель в геноме второй популяции q 2 при взаимодействии с первой популяцией встраивается в геном первой популяции с катастрофическими для клетки первой популяции последствиями. Следовательно, можно предположить, что мутагенный фактор D 21 - « i q 2 , где « 1 <  0 - некоторый постоянный коэффициент.

Воздействие первой популяции на вторую заключается в уничтожении иммунной системой первой популяции особей (вирусов) второй популяции. Следовательно, можно предположить, что D 12 - « 2 , причем величина « 2 <  0.

Выражение в скобках примем равным нулю:

Y — + In 2u - 0. Интегрируя это равенство, най-dn                    n                         n дем In u -----In2 у . Следовательно, u - 2 Y.

Y

Постоянную интегрирования принимаем равной нулю, т. к. имеется некоторый произвол в выборе функции u . Подставляя эту функцию в (8), получим:

n

Y 2 2 у vL - ™ n + C dn

Решаем уравнение (9) относительно функции v , сначала находим:

I n

n )

dv -

v

^a 2

n 2 Y + C L 2 Y dn .

Y Y

Следовательно:

I n _ n)

-J

^a 2

Y

n 2 . C 2 ⁷ dn -

Y Y

Y

n

n

₌ ^2_ n I d 2 Y + C 1 ² ln 2 J ( у J        у In 2

+ C 2 =

^a 2

ln 2

f n n 2 у у

n 1 n

2 ^Y     C i 2 ^Y

;—г +--;—r + C

In2     у In 2

nn a2 2Y f n   1 1 C1 2Y

---------1--I +----+ C q

In2 (у In2 J у In2

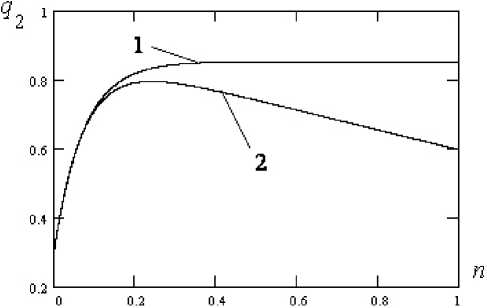
Рис. 1. Изменение частоты аллеля q ₂ со временем для второй (вирусной) популяции при отсутствии воздействия иммунной системы первой (человеческой) популяции, кривая 1 и при наличии воздействия, кривая 2. Параметры расчета: q 0 = 0,3; q ₂ z = 0,65; у= 0,05; a ₂ =- 0,01

Fig. 1. Change in the frequency of the q ₂ allele with time for the second (viral) population in the absence of exposure to the immune system of the first (human) population, curve 1 and in the presence of exposure, curve 2. Calculation parameters: q ₀ = 0,3; q ₂ z = 0,65; у = 0,05; a ₂ = - 0,01

Таким образом, для частоты аллеля q 2 найдем:

^a ₉ f П 1 1 ^C 1

q₉ = uv = —I -    |+— ¹

In2 (у In2 J у In2

n

+ C 2 2 ^у .

Используем следующие условия: при n = 0 частота аллеля q 2 = q 20 , при n = р"^ частота аллеля q 2 = q 2 z . Второе условие эквивалентно времени t = 1,443 T 2 , т. е. второе условие принимается для времени, примерно в полтора раза больше среднего времени жизни особи второй популяции.

Следовательно, по первому условию:

( J (

^q 20 =

-

^a 2

ln2 2

₊ ^C 1 ¹

у ln 2

^{+ C} 2 ,

1 - 2 ^{ln 2}

по второму условию:

q 2 z

C ₁ 1 у In2

1_ + C 2 2 ^{ln 2}.

^a 2 ln² 2

n ln 2 - ^у

- n 1

^{1 - 2 у}

-

1 - 2 ^{ln 2}

J

Решая систему (13), (14), находим:

^q 20 ^- q 2 z ⁺

C 2 =

^a 2 ln² 2

1_

1 - 2 ^{ln 2}

_c .   q 2 z - q 20 2 -^--^Hini

^C 1 ¹ = ln² 2

у ln 2                     ¹

1 - 2 ^{ln 2}

Подставляя (15) и (16) в (12), получим:

a₉ n q₀ = ²— + ⁴²   ln2 у

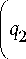
-“2- 1 ln² 2 J

f - n

^{1 - 2 у +} q 20

n

+

( J

1 1

- 2-Ы

J

1 - 2 ^{ln 2}

Формулу (17) можно записать в виде суммы, отражающей размножение во второй (вирусной) популяции и воздействие на нее первой популяции:

Отметим, что размножение вирусной популяции происходит не самостоятельно, а только при взаимодействии с клетками, например, человеческой популяции. Поэтому в первом слагаемом

T

(18) присутствует величина у = —, зависящая от T ₁

среднего времени жизни клеток первой (человеческой) популяции. Второе слагаемое (18) отражает действие иммунной системы человека на вторую (вирусную) популяцию.

На рис. 1 показано изменение частоты аллеля q 2 второй (вирусной) популяции со временем при отсутствии воздействия иммунной системы человека, кривая 1, и при наличии воздействия, кривая 2, со стороны иммунной системы первой популяции.

Из анализа графиков видно, что при отсутствии воздействия иммунной системы человеческой популяции на вирусную популяцию происходит постепенный рост частоты аллеля q ₂ со временем, приближение частоты аллеля q ₂ к равновесному значению. При наличии воздействия иммунной системы первой (человеческой) популяции рост q ₂

сменяется падением за счет гибели вирусов при действии иммунной системы первой популяции.

Подставляя (24) в (20), найдем:

3. Развитие человеческой популяции во время пандемии

2 A + ²---- -ln 2 ( 2 An + B ) +

Наиболее интересный вопрос - это взаимодействие клеток органов человеческой популяции при взаимодействии их с вирусами. Некоторые результаты такого взаимодействия можно получить при решении уравнения (4).

Решение уравнения (4) принципиально можно получить, подставляя решение (18) в уравнение (4). Однако такой путь затруднен появлением сложной функции в правой части уравнения (4). Поэтому мы увеличим порядок уравнения, подставив функцию q 2 из уравнения (4) в уравнение (5). В результате получим линейное дифференциальное

+— ln 2 ( An + Bn + D ) =

a 1 a 2	r
2
Y 2	(

n

——+ C з n + C

Приравнивая коэффициенты степенях n , находим:

a a a = —,

2 y ln²2

a a

B = -1^- с з

Y ln² 2

-

' 4

.

при одинаковых

a1a2—V

Y ln³ 2

.

Постоянную D в (24) находить нет необходимости.

Таким образом, частное решение (24) уравнения

(20) принимает вид:

^a 1 ^a 2

q f ¹ = Y ln 2 2

n

+

'3    In 2

A A

■ n + D.

уравнение четвертого порядка:

• Y 2 d f + , ( , + 1 ) In2 d A f . +

dn               dn dqf1

• + Y ln 2--- — = а_ла. .

dn ^{2    12}

Интегрируя уравнение (19) дважды, находим:

Следовательно, решение уравнения шется как сумма (23) и (27):

q f 1 = C 5^{2 - n}

n

+ ^C 6^{2 Y} +

(20) запи-

« 1 « 2

Y ln² 2

( 2 n_

'3    ln 2

A A

■ n + D.

d qf1 dn2 (H1) ln 2 dqf1 Y       dn +—ln 2q ri = Y       f (20) 2 a1a2 = Y2 n 2 — + C 3 n + C 4 I 2             7 , где C3 и C4 – постоянные интегрирования.

Для решения уравнения (20) сначала найдем общее решение однородного уравнения. Запишем

Примем начальное условие: при n = 0

q f 1 = q f ° .

Следовательно:

q f 0 = C 5 ⁺ C 6 ⁺ D .

Таким образом:

величина

q f 1 = q f 0 ^{+ C} 5 ( ² n - 1 )

+ C 6

^ - n A

2 ^Y - 1

+

характеристическое уравнение:

k2 + 11111 in2k + 1 ln2 2 = 0.

YY

Решения квадратного уравнения (21) имеют вид:

k =- in 2, L =-—.

Следовательно, общее решение однородного

. ^a1 ^a 2

Y ln² 2

n

+

A A

'3    ln 2

n

.

уравнения:

q f 1 = C 5 e k ^{1 n} + C 6 e^{k 2 n} =

- ln 2 n               - n

= C ₅ e ^{- ln 2 n} + C 6 e    ^Y= C ₅ 2 - ⁿ + C 6 2 ^Y ,

где C ₅ и C ₆ – постоянные интегрирования.

Частное решение уравнения (20) будем искать в виде полинома:

q f 1 = An ² + Bn + D ,                             (24)

где A , B и D – постоянные коэффициенты.

Полученное решение (30) характеризует сумму двух процессов: размножение особей первой популяции – первые три слагаемых и воздействие на популяцию – четвертое слагаемое.

Отсутствие воздействия на первую популяцию возможно в двух случаях. Во-первых, при « 1 = 0, т. е. вторая популяция не действует на первую; во-вторых, при « 2 = « 1 = 0 - популяции развиваются независимо друг от друга; в-третьих, при нулевом значении выражения в скобках четвертого слагаемого (30).

Последний случай наиболее интересен. Он связан с вариантом, когда на первую популяцию, например человеческую, воздействие второй популяции, например вирусной, было, но затем оно

прекратилось, т. к. человеческая популяция выработала иммунитет к воздействию вирусной популяции.

Приравняем последнюю скобку (30) к нулю:

n

3 ln 2

V             7

— 0.

Уравнение (31) позволяет найти безразмерное время выработки иммунитета у первой популяции к воздействию второй популяции:

п =2 èìì

—

ln 2

V

)

C 3

.

Размерное время равно:

t uMM — ^{2 T} 1

ln 2

V

—

) C 3

.

К сожалению, формула (33) содержит неопределенную постоянную величину C ₃ .

Постоянная C ₃ определяется, согласно (19), суммой начальных значений первых трех произ-

водных по времени от частоты аллеля q_{f 1} грируя (19) один раз, при n — 0 найдем:

. Инте-

У

, 2 d q f 1

dn ³

V 7

+ ? ( ? + 1 ) ln 2

Г л2. ) d q f 1 dn ²

+

+ у ln²2

Г dq f 1 ' dn

— а^ C з .

T

Будем считать у — очень маленькой величи ной. Это возможно, т. к. среднее время жизни клеток человека обычно много больше среднего времени жизни вируса. В этом случае, согласно (34), постоянная C3 ® 0.

Формула (30) при C з ® 0 и у <<  1 приобретает вид

q f 1 ^— q f 0 ⁺ C 5 ( ² n ^— 1 ) ⁺ C 6

Г _— n '

2 ^Y — 1

+

а^ 2 у ln² 2

Г n ² ( Y + 1 )

—

V

ln 2

) ⁿ

.

При C 3 ® 0 безразмерное время затухания воздействия второй популяции на первую (32)

равно n èìì t — — T uMM ln2 1

—---® ln2

« 2,9 T 1

2,9, размерное время (33) - ® 400 суток. Получившееся

время возникновения коллективного иммунитета – почти 3 средних времени жизни клетки особи.

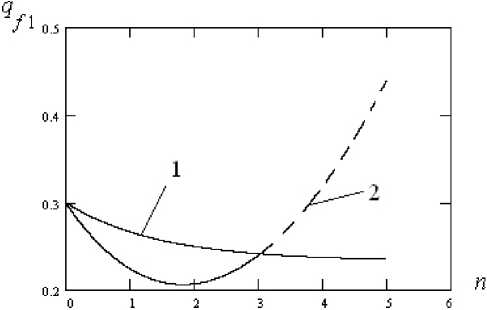
Рис. 2. Изменение частоты аллеля q_{f 1} со временем у первой (человеческой) популяции при отсутствии воздействия второй (вирусной) популяции, кривая 1, и при наличии воздействия, кривая 2. Параметры расчета: qf ₀ — 0,3; qm ₀ — 0,1; у — 0,05; а 1 — — 0,1; а ₂ — — 0,01

Fig. 2. Change in the frequency of the q_{f 1} allele with time in the first (human) population in the absence of exposure to the second (viral) population, curve 1 and in the presence of exposure, curve 2. Calculation parameters qf ₀ — 0,3; qm ₀ — 0,1; у — 0,05; а 1 —— 0,1; а ₂ — — 0,01

После окончания воздействия второй популяции на первую последнее слагаемое в (35) становится равным нулю. Происходит свободное размножение первой популяции. Учитывая также у <<  1, можно записать:

q f 1 — q f 0 + C 5 ( 2 ^{— n} — 1 ) — C 6 . (36)

Закон свободного размножения популяции имеет вид [1]:

q f 1 —

² q f 0 ⁺ q m 0

q f 0 q m 0

V           7

2 ^{— n}

где q f 0 - начальная частота рассматриваемого рецессивного аллеля у женщины, q_{m 0} – у мужчины.

q f 0 q m 0

Сравнивая (36) и (37), находим C 5 — —— --- .

Как и следовало ожидать, получилось C ₆ — 0, т. к. q_{f 1} при свободном размножении особей не должно зависеть от величины у . Поэтому формулу (35)

можно переписать в виде

^q f 1 ^{— q} f 0

(л. -л qf 0  qm 0

V           7

^{— 1 )+}

^а 1 ^а 2 Г n ² ।    1 ) J

n у ln2 2 V 2    ln2   7

На рис. 2 показано изменение частоты аллеля q _{f 1} первой (человеческой) популяции со временем при отсутствии воздействия, кривая 1, и при наличии воздействия, кривая 2, со стороны второй (вирусной) популяции.

Из рис. 2 видно, что частота аллеля при отсут- ствии

пенно

чению

воздействия вирусной падает, приближаясь к

• ²    q f 0 + q m 0

qf i =      3-----= 0,23- популяции посте-равновесному зна-

При воздействии

вирусной популяции частота аллеля, на который осуществляется воздействие, кривая 2, сначала падает очень быстро за счет гибели клеток и, соответственно, аллелей, но затем, по мере выработки иммунитета при пимм =-—-® 2,9 и размножения клеток, частота возрастает, достигая нормального уровня, соответствующего кривой 1. Дальнейший рост кривой 2, показанный пунктиром, по-видимому, биологического смысла не имеет.

Заключение

Использованная генетико-математическая модель взаимодействия популяций, основанная на законе Харди – Вайнберга, позволяет рассчитать некоторые характерные особенности процесса взаимодействия популяций. Ее можно использовать при оценке длительности пандемии COVID-19.

Отмечено, что вирусная популяция взаимодействует не с человеческой популяцией как совокупностью очень сложных организмов, а с популяцией отдельных клеток органов человека. В качестве примера использованы клетки печени. Показано, что длительность процесса пандемии в этом случае составляет примерно 400 суток.

С помощью уравнений развития популяции показано, что клетки человеческой популяции сначала интенсивно гибнут под воздействием вирусов, но затем, при выработке иммунного ответа, за счет размножения клеток, орган человека восстанавливается до нормального уровня. Гибель особи (человека) при вирусной атаке является достаточно эксклюзивным событием, связанным с полным поражением уже заранее ослабленного по сопутствующим причинам органа.

Показана динамика развития вирусной популяции при взаимодействии ее с человеческой популяцией. Рассчитана интенсивность гибели вирусов, в частности гриппа как хорошо изученного заболевания, при действии иммунной системы человека.