Геодинамический мониторинг крупномасштабных систем на основе математических моделей

Задачи управления крупномасштабными системами, в особенности сложными распределенными природно-техническими системами, относятся к разряду задач оптимального управления стратегического характера. Отличительной особенностью управления такими системами в современных условиях является обеспечение их безопасности в условиях возможного проявления опасных природно-техногенных процессов. События, произошедшие в Японии в марте 2011 года, показали крайнюю незащищенность населения и территорий при реализации опасных природных процессов геодинамического происхождения, точнее, кульминации этих процессов – высокоэнергетических сейсмических событий.

С этой точки зрения, для обеспечения безопасности крупномасштабных систем необходим постоянный высококачественный мониторинг их геологической среды (геосреды). Такой мониторинг в настоящее время основывается либо на методах традиционного качественного описания, либо проведения исключительно приборных исследований, которые позволяют отслеживать реализацию опасных геодинамических со- бытий в режиме реального времени, но затрудняют возможность осуществления превентивных мероприятий.

При подобном подходе остаются нерешенными такие проблемы, как неполнота информации о пространственно-временном распределении внешнего воздействия на систему и неопределенность в поведении системы. То есть мониторинг должен быть ориентирован на оценку динамики опасных геодинамических процессов посредством выявления пространственного распределения и количественной оценки зон геодинамического риска. Традиционно используемыми в настоящее время являются технологии оценки динамики опасных геодинамических процессов на основе статистических данных о пространственно-временном распределении таких процессов. А если такой статистики нет или ее недостаточно?

В этом случае, по мнению авторов, мониторинг должен обязательно включать в себя использование современных эффективных математических моделей, позволяющих превентивно количественно оценивать зоны геодинамическо-го риска, т.е. с позиций математического моделирования возможно разрешение обеих обозначенных нами выше проблем.

Проблема неполноты информации о пространственно-временном распределении внешнего воздействия на систему решается посредством комплекса математических моделей оценки гео-динамической устойчивости крупномасштабных систем, базирующихся на способе восстановления полей геодинамических и смещений, основанном на разложении аномального гравитационного поля в изостатической редукции на составляющие его зональные гармоники [1].

В таком случае распределенное внешнее воздействие P(x, у) , известные дискретные значения которого заданы с некоторым фиксированным шагом по осям X и Y , представляется в виде:

Р оо 1 V 1            X

^{P ( x} , У ) = —- + тЕ Р т 0 +т £ Р 0 n + ZZ P mn , (1) ^{4     2} т = 1          ² n = 1          т = 1 n = 1

где, например,

p„ „ = am „ cos kx cos к у + h „ sin kx cos к у + mn mn x        y mn x        y

+ c cos k x sin k у + dmn sin kx sin kv;

mn x       y mn x       y

4 “ ⁶

a_mn = — jj P ( x , У )cos k x x cos k y ydxdy ;

ab 0 0

_ nm_    nn kx =    ; k = ——; a, b - соответственно длина a yb

• ( X) и ширина ( Y) рассматриваемой территории;

p(x, у) - величины изостатических аномалий гра- витационного поля.

Тогда компоненты тензора напряжений и составляющие вектора смещений в геосреде представляются аналогичным образом, например для нормальных компонент тензора напряжений со- отношением вида:

s

¹ —(00) , ¹      _( т 0) .

• <0 ,( x , у , Z ) = О () +- 7 < 0 ( ) + с е                        а                  а

• 4         2 т =1

lsl

• + 1 Z o a° n ) +ц о а ™) ,

• ² n = 1            т = 1 n = 1

  
  

где а е { x , у , z , } .

Подобный подход является весьма эффективным с экономической точки зрения, поскольку не предполагает проведения приборных исследований. Анализ рассчитанных компонент тензора напряжений и составляющих вектора смещений позволяет строить пространственно-распределенные карты-схемы возможного проявления опасностей геодинамического происхождения, на которых представлены величины относительной плотности потенциальной энергии деформируемых пород геосреды (рис. 1).

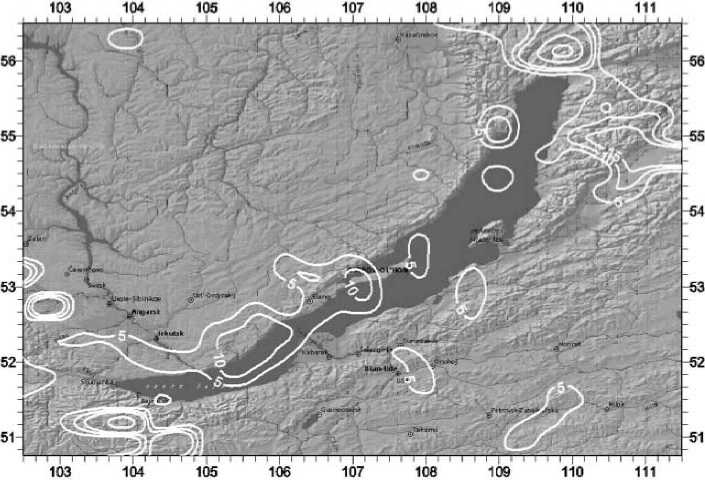
Рис. 1. Карта-схема распределения величин относительной плотности потенциальной энергии деформируемых пород геосреды на территории Байкальского региона

Для решения проблемы неопределенности в поведении систем предложен математический метод вероятностной оценки геодинамического риска [2]. Он основан на представлении возможных геодинамических состояний среды как про- стейшего потока геодинамических событий с последующим построением системы дифференциальных уравнений Колмогорова относительно вероятности нахождения среды в этих состояниях (рис. 2).

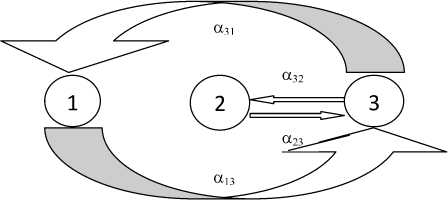
Рис. 2. Схема взаимопереходов геосреды по состояниям 1, 2, 3

При составлении системы уравнений для вероятностей p 1 (t) , p ₂ (t) , p ₃ (t) нахождения среды в состояниях 1, 2, 3 определяются интенсивности процессов a j (где г = 1, 2, 3; j = 1, 2, 3), физически представляющих собой сумму энергетических параметров процессов, протекающих в системе, окончание которых приводит к непосредственному переходу системы из состояния i в состояние j . Тогда изменения указанных вероятностей будут описываться следующей системой дифференциальных уравнений Колмогорова:

' p ‘ ⁽ t ) = ^-а 13 Р 1 ⁽ t ) + ^а 31 Р 3 ⁽ t ), _<  Р ‘ ⁽ t ) = ^{- а} 23 Р 2 ⁽ t ) + ^а 32 Р 3⁽ t ), ^p 3 ⁽ t ) = ^a 13 ^p 1 ⁽ t ) + ^a 23 ^p 2 ⁽ t ) — ^{( a} 31 + ^a 32 ) ^p 3 ⁽ t ), . p , ⁽ t ) + p ₂ ⁽ t ) + p 3 ⁽ t ) = 1.

Интенсивности процессов ^a j оцениваются на основе информации о величинах деформаций в геосреде, вертикальных, горизонтальных смещений в геосреде (и их градиентах), полученных по данным математического моделирования. Подобный подход позволяет строить прогнозные карты-схемы пространственного распределения комплексного геодинамического риска для систем любого масштабного уровня и целевого назначения с достоверностью выходных карт-схем 0,9 (после соотнесения расчетных прогнозных данных с распределением геодинамических (в частности, сейсмических) событий, произошедших в тестовых регионах после выполнения расчетов) (рис. 3).

К сожалению, точный прогноз высокоэнергетических опасных геодинамических событий и в особенности катастрофических землетрясений на сегодняшний день остается тайной за семью печатями. Тем не менее, авторы надеются на то, что дальнейшие их разработки в области применения методов математического моделирования и численных методов к изучению опасных гео-динамических явлений позволят приблизиться к решению этой очень важной для всего человечества проблемы.

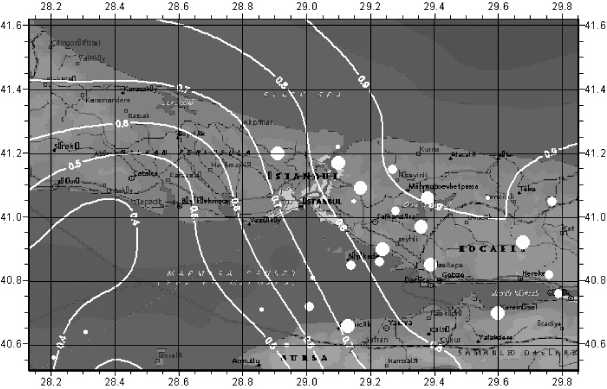
Рис. 3. Карта-схема пространственного распределения вероятностного комплексного геодинамического риска для окрестностей Стамбула с эпицентрами произошедших в 1999-2008 гг. землетрясений (с магнитудами от 3,8 и до 5,2)