Геоэкологические аспекты транспорта наносов в водных объектах: новые подходы и формулы

Оценка, прогноз и моделирование последствий неблагоприятных внешних воздействий на природные системы являются одной из важнейших прикладных задач геоэкологии. Моделирование в геоэкологии – это инструмент количественной оценки переменных состояния природных систем, определяющих среду обитания живых организмов. Применительно к водным объектам встают вопросы, связанные с негативным влиянием повышенной мутности воды и заиления водоемов на функционирование водных экосистем. Успешное решение проблем оценки и прогноза экстремального поступления наносов в водные объекты в приложении к рекреационным, рыбохозяйственным и водохозяйственным задачам зависит от организации научно обоснованного мониторинга и развития современных методов расчета стока наносов, их транспорта и пространственно-временного распределения в водных объектах.

Наиболее актуальны расчеты твердого стока и мутности воды при решении следующих водохозяйственных и геоэкологических задач:

– заиление водохранилищ;

– нормирование сбросов сточных вод при оценке фоновой мутности водоприемника;

– проектирование водозаборов (здесь актуальны вопросы как размещения оголовков в пределах водного объекта, так и определение технических характеристик очистных фильтров водозабора);

– при оценке ущербов планируемых гидротехнических мероприятий в пределах водного объекта или на его водосборе (например, выемка донного грунта, приводящая к увеличению мутности водного объекта и, как следствие, формирование неблагоприятной среды обитания для гидробионтов);

– при планировании или ведении рекреационной или рыбохозяйственной деятельности на водном объекте

– при оценке вероятности наступления (опасного) неблагоприятного геоэкологического явления, связанного с повышенным твердым стоком.

При этом наиболее востребованы расчеты интенсивности заиления водохранилищ, оцен- ка статистических параметров распределения мутности воды, пространственно-временного распределения мутности в акватории, динамики переформирования дна водного объекта и так далее.

ПОСТАНОВКА ЗАДАЧИ

Существующая в настоящее время сеть наблюдений за гидрологическим режимом и показателями качества воды, а также система проведения наблюдений на отдельных водных объектах не могут в полной мере обеспечить достоверный для последующих обработки и анализа материал. Причина этого состоит в редких и нерегулярных отборах проб, а также недостаточном количестве наблюдательных пунктов.

Ввиду этого в последнее время нашли свое развитие методы обобщения гидрохимической информации и данных о мутности для года, что дает относительно приемлемую основу для последующей статистической оценки среднегодовых показателей качества воды и режима твердого стока [Шелутко, Колесникова, 2008; Смыжова, 2010; Шелутко, Студеникина, 2013].

В условиях редких и неэквидистантных наблюдений невозможно полноценно проработать вопрос статистической оценки вариационных рядов суточных данных. Этому вопросу также посвящено достаточно много работ как у нас, так и за рубежом [US EPA, 2000; Шелутко, Колесникова, 2008; Смыжова, 2010; Лепихин, Возняк, 2012; Шелутко, Студеникина, 2013; Лепихин, Головачева, 2015]. Проблемы начинаются на этапе идентификации закона распределения, которому подчиняется вариационный ряд. Часто при статистическом анализе рядов гидрохимических показателей останавливаются лишь на оценке медианы и квартильного размаха. Таким образом, вопрос оценки экстремальных значений показателей качества воды редкой обеспеченности остается открытым. Редкость и нерегулярность наблюдений также не позволяет достоверно выявить выбросы иного от естественного формирования генезиса. Все это приводит к смещению в параметрических и непараметрических оценках вариационного ряда. Принципиально решить эту проблему возможно лишь организацией достойного мониторинга за показателями качества воды – регулярным с малой дискретностью отбором проб на взвешенные вещества.

Однако на текущем этапе состояния наблюдательной базы при достаточно изученных процессах формирования физических и гидрохимических потоков и общего массопереноса в системе «водосбор – водный объект» крайне эффективными остаются методы математического моделирования. Как в России, так и за рубежом разработаны модели и расчетные методы для количественной оценки пространственновременных закономерностей распространения потоков вещества в указанной системе разного масштаба – от мгновенных (секундных) до среднегодовых. Причем в зависимости от назначения модели, выделяют детерминированные и стохастические подходы. Расчеты массо-переноса в системе «водосбор – водный объект» должны быть представлены комплексом математических моделей, последовательно описывающим основные взаимосвязанные природные процессы – погодная (климатическая или метеорологическая) модель, модель эрозии почвы, модель формирования стока на водосборе, гидродинамическая модель двухфазного речного потока и модель гидродинамики и транспорта наносов в водоеме. В последнее время набирают популярность детерминированно-стохастические системы, позволяющие существенно расширить возможности детерминированного моделирования особенно в части недостаточности или отсутствия наблюдений за одной из переменных состояния системы или при реализации различных численных экспериментов.

Развитие детерминировано-стохастических методов в оценке стока наносов в водном объекте предполагает наличие надежных детерминированных расчетных схем, достоверно описывающих физику процессов массопереноса. Транспорт наносов в речном потоке, мутность воды, переформирование дна – это процессы, в основе которых лежит принцип пространственно-временного перераспределения твердого вещества в водном объекте.

В настоящее время существует большое количество формул для расчета расхода взвешенных и влекомых наносов, общего расхода наносов, транспортирующей способности потока. При этом высокий порядок степени аргументов в формулах транспорта наносов в речном потоке приводит к большой ошибке вычислений. Также, одной из значимых ошибок расчета по таким формулам является использование в качестве аргумента квантиля крупности донных отложений, который отличается большой изменчивостью в русле реки. Для объективной оценки значения этой величины требуется отбор проб донного грунта всего поперечного сечения водотока, что в ряде случаев не представляется возможным. Известные формулы расчета расхода наносов не учитывают взаимосвязанное влияние гидравлики потока и переносимых им твердых частиц. Также вопрос задания параметров трения на твердой границе речного потока, несмотря на многолетние исследования этого процесса, остается до сих пор недостаточно изучен.

Известные проблемы в точность вычислений привносят и алгоритмы расчета транспорта наносов, разработанные отдельно для взвешенной и влекомой форм перемещения твердой фазы в речном потоке. Движение наносов обусловлено лишь энергией потока и крупностью транспортируемых частиц. Речной поток характеризуется транспортирующим потенциалом, в соответствии с которым определяется и количество (масса) перемещаемых частиц. И в зависимости от гранулометрического состава транспортируемого материала часть наносов поднимается в водной толще и переносится водным телом потока, а часть волочится и перекатывается по дну. Причем соотношение взвешенной и влекомой форм транспорта крайне изменчиво. Оно зависит от гидродинамического режима потока и поступления твердого вещества извне (например, со стороны водосбора или в результате отвала грунта в русле реки). Гидродинамический режим потока в свою очередь определяется неравномерностью русла, изменчивостью уклона и крупностью донных отложений, а также расходом воды и наносов верхнего створа.

Создание способа расчета общего расхода наносов, построенного на балансе сил, действующих в двухфазном речном потоке, позволит учесть взаимосвязанное влияние гидравлических переменных состояния потока и переносимого потоком твердого вещества. При этом основной камень преткновения речной гидравлики – взаимодействие движущегося потока и дна, следует рассматривать не со стороны пограничного слоя жидкости, а со стороны донных отложений, их хорошо изученных в грунтоведении свойств. Задание крупности донных отложений посредством их качественной характеристики (категориями, которые включают в себя широкие диапазоны изменения крупности) позволяет уйти от ошибок расчета, возникающих при использовании конкретных значений квантилей донных отложений.

РАЗРАБОТАННЫЕ МЕТОДЫ И МОДЕЛИ

В институте Озероведения РАН разработана методология решения геоэкологических задач, связанных с оценкой твердого стока водных объектов [Шмакова, 2018]. Методология представлена принципами исследования (взаимосо-пряжение и взаимоопределение твердого стока и гидравлических переменных состояния потока) и основанным на них комплексом следующих методов и моделей:

• 1.    Математическая модель движения воды и твердого вещества. Модель позволяет оценить гидравлические переменные состояния потока, расход наносов, а также интенсивность распространения примеси в речном потоке. Модель является сопряженной, то есть в ней предполагается взаимосвязанный расчет гидравлических переменных состояния потока и твердого вещества. Параметры трения в модели представлены физически обоснованными параметрами – ко-

• эффициентом внутреннего трения и сопротивлением частиц грунта сдвигу.

• 2.    Аналитическая формула расхода наносов и основанная на ней формула транспортирующей способности потока позволяют со достаточной точностью (в сравнении с формулами того же типа) оценить расход наносов (или мутность воды) и максимальную взвесенесущую нагрузку потока (максимальный расход наносов или максимальную мутность при заданном расходе воды). Формулы обеспечиваются данными стандартных гидрометрических наблюдений, имеют простую структуру и физически обоснованные параметры. Интеграция этих формул в гидродинамические модели водоемов предоставляет возможность получать поля распространения мутности воды и расхода наносов в том числе и при допущении о максимальной нагрузке водного потока взвешенными веществами, например, при дноуглубительных работах.

• 3.    Двумерная модель гидродинамики и транспорта наносов в мелководном водоеме. Модель основана на совместном решении уравнений мелкой воды в двумерной постановке и аналитической формулы расхода наносов. В качестве алгоритма переформирования дна рассчитывается изменение транспортирующего потенциала потока между двумя расчетными створами. Модель позволяет рассчитывать пространственно-временные закономерности распространения расхода наносов, мутности воды в акватории, динамику переформирования дна, вызванную нестационарным режимом водного объекта, а также прогнозировать режим мутности при неблагоприятных гидрометеорологических явлениях.

• 4.    Стохастическая модель годового твердого стока. Модель основана на аналитической формуле расхода наносов и композиционном методе теории вероятности и позволяет оценить параметры распределения стока наносов и мутности в разных временных масштабах. Дополнительные возможности модели состоят в возможности оценки статистических параметров твердого стока при изменении гидравлических переменных состояния водотока – глубины, расхода воды и уклона, произошедших в результате естественных причин или хозяйственной деятельности в русле реки или на ее водосборе.

Приведенная выше методология дополнена новыми алгоритмами оценки расхода взвешенных и влекомых наносов.

НОВЫЕ ПОДХОДЫ И ФОРМУЛЫ

Концепция фазового гидравлического пространства (или пространства состояний гидравлических переменных двухфазного речного потока) подробно рассмотрена в [Shmakova, 2022]. В основе этой концепции лежит соотношение средней глубины и скорости потока в пределах одного расхода воды (рис. 1). Каждому сочетанию глубины и скорости соответствует расход наносов G=[0; Gmax], где Gmax – максимально возможное количество наносов, переносимое данным расходом воды за единицу времени или транспортирующая способность потока. При G=0 поток будет осветленным и его скорость будет минимальной, а глубина возрастет. G=[0; Gmax], где Gmax – максимально возможное количество наносов, переносимое данным расходом воды за единицу времени или транспортирующая способность потока. При G=0 поток будет осветленным и его скорость будет минимальной, а глубина возрастет. При G=Gmax скорость возрастет, а глубина потока уменьшится [Vanoni, 1963; 1980].

Фазовое гидравлическое пространство характеризуется морфометрией русла и характером подстилающей поверхности, а транспортирующий потенциал потока определяется в соответствии с количеством поступившего в поток твердого вещества. Вид функции, аппроксимирующей фазовое гидравлическое пространство, определяется формой поперечного сечения, а сама функция представляет собой соотношение скорости и глубины для постоянного расхода воды в расчетном створе.

V,m/s g=const

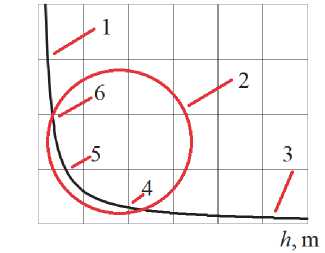
Рис. 1. Схематичное представление фазового гидравлического пространства для русла прямоугольной формы (1 – область максимально возможной нагрузки на поток; 2 – область физически возможных значений; 3 – осветленный поток; 4 – неразмывающая скорость (начало движения взвешенных частиц);

5 – срывающая скорость (движение взвешенных и влекомых наносов); 6 – незаиляющая скорость)

В пределах возможного диапазона изменения своих значений при заданном расходе воды, скорость потока может соответствовать критическим значениям, которые определяют условия транспорта наносов и изменения отметок дна. Например, для двухфазного речного потока выделяют следующие критические скорости [Карасев, 1975]:

• . неразмывающая скорость (предельная скорость, при которой основная часть донного грунта находится в состоянии покоя);

. срывающая скорость (начало массового передвижения частиц);

. незаиляющая скорость (предельная скорость, при которой частицы остаются во взвешенном состоянии).

В частности, В.Н. Гончаров дает такое определение срывающей скорости: «наименьшая средняя скорость потока, при которой происходит уже беспрепятственный срыв отдельных выступающих зерен на дне и при которой средний уровень пульсационных подъемных усилий на них примерно равен весу зерна в воде» [Гончаров, 1962]. Такое определение позволяет сделать вывод о том, что срывающей скорости потока соответствует начало движения частиц как во взвешенной так и влекомой форме. Согласно определению Е.А. Замарина [Замарин, 1951], «незаиляющей скоростью называется та наименьшая средняя скорость течения, при которой содержащиеся в воде взвешенные наносы не выпадают из потока». Очевидно, что область осветленного потока будет характеризоваться нижним пределом неразмывающей скорости, тогда как область максимальной взвесенесущей нагрузки на поток – незаиляющей скоростью. При этом полагается, что начало движения частиц в речном потоке преимущественно сальтацией и во взвешенной форме соответствует скорости, находящейся в диапазоне между неразмывающей и срывающей скоростями. Последнее можно объяснить тем, что при падении транспортирующего потенциала речного потока при перемещении разнофракционных наносов первыми откладываются на дно частицы наибольшей крупности. Верхний же слой отложившихся наносов будет представлен тонкодисперсными фракциями. Тогда при увеличении транспортирующего потенциала первым в движение придет верхний слой донных отложений, представленных частицами наименьшего размера. В подтверждение последнему рассмотрим выражения, полученные для критических скоростей начала движения влечением v_{cr bed} и взвешиванием v_{cr suspend} [Soulsby, 1997]

V crbed = 5.751g | 2 A | 9 crbed | ^- - 1 | gd ₅₀ ,

I ^d 50 Л    I P w )

cr suspend

_ .      ( 12 h I L

— ⁵.^751g I        I ⁹ crsuspend

( 6 d 50 )

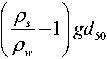
9 crbed — TTT^ ⁺ 0.055 ( 1 - exp [ - 0.02 D * ] ) , I .

9 „suspend — 1Цг + 0.1 ( 1 - exp [ - 0.05 D * ] ) ,

D ^— d 50

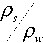
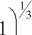
где d ₅₀ – диаметр частиц, обеспеченностью 50 %, м; g — ускорение свободного падения, м/с²; v -коэффициент кинематической вязкости, м²/с; р _s и р w - плотности грунта и воды соответственно, кг/м³; h – средняя глубина потока, м.

Из этих соотношений следует, что движение взвешенных частиц, крупность которых менее 30 % общей крупности частиц, перемещающихся влечением, определяется меньшим значением критической скорости. В условиях большого гранулометрического разнообразия минеральных частиц, находящихся в речном русле, это означает, что начало движения наносов придется на взвешенную форму. При этом, имеет место следующее соотношение критических скоростей потока и характера транспорта разнофракционных наносов:

v ₁ – скорость, меньшая минимальной неразмывающей скорости (движения наносов нет G =0);

. v ₂ – неразмывающая скорость (начало движения взвешенных наносов G_suspend );

. v ₃ – срывающая скорость (начало движения влекомых и взвешенных наносов G_{suspend+bedload} );

. v ₄ – незаиляющая скорость (транспортирующая способность потока G _max ).

Рассмотрим вывод формул расхода взвешенных и влекомых наносов и транспортирующей способности потока.

Аналитическая формула общего расхода наносов имеет вид

max

—P—Q

P s ^- P w

3 L ^{P s p}w ^Q g 3

N    P s   B g

- (1 - f ) P w I

где B – ширина потока, м.

Формулы расхода взвешенных и влекомых наносов. Начало взвешивания наносов сопряжено с превышением средней скорости потока над неразмывающей скоростью. Полученная на основании многочисленных исследований формула неразмывающей скорости потока v_cr имеет вид [Студеничников, 1964]

ver = L15 Vg (herd )0.25.      (3)

где d – средний диаметр частиц, м.

Выразив из выражения (3) глубину, получим

hcr

v c 4 r

1.154g2d

Подставляем полученное выражение (4) в формулу общего расхода наносов (1) и получаем формулу для расхода взвешенных наносов G_suspend G suspend = ^—Q [ 1.15 4 cgd - ( I — f ) i P w 1 . (5)

P s ^- P w V v              )

где v – скорость потока, м/с.

Исходя из того, что общий расход наносов представляет сумму расходов взвешенных и

G =

P s

P s — P w

с

Q у— (1 — f ) I P w .

_ hg

влекомых наносов, получим выражение для расхода влекомых наносов G bedload

G,   , = G - G bedload             suspend ,

где р _s и р w - плотности грунта и воды соответственно, кг/м³; Q – расход воды, м³/с; f – коэффициент внутреннего трения, б/р; c – параметр сцепления частиц грунта при сдвиге, кг/(м·с²); g – ускорение свободного падения, м/с²; I – уклон дна, б/р; h – средняя глубина потока, м.

Эта формула является следствием основного уравнения движения воды и твердого вещества в речном потоке [Шмакова, 2018], которое основано на балансе сил, действующих в системе «водный поток – донные отложения – наносы» на движущуюся частицу наносов. Параметры f и c формулы (1) зависят от фазы водности водотока и крупности донных отложений.

Исходя из концепции фазового гидравлического пространства полагаем транспортирующую способность потока Gmaх равной расходу наносов при максимальном значении скорости потока (и минимальной глубине). Процедура выводы формулы транспортирующей способности потока и ее апробация приведены в [Shmakova, 2022]. Формула основана на аналитической формуле расхода наносов [Шмакова, 2018], формуле сопротивления грунта сдвигу [Бабков и др., 1950] и формуле граничной скорости осаждения частиц в потоке воды [Лямаев, 1988] и имеет вид bedload

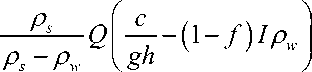
—^P^e ^[ 1.15^{4 eg}- - ( 1 - f ) i p _ I ,

Ps - Pw  V v             )

C —    ^Ps        ¹ — 1 1 S 4 ^gd

^Gb>edloaid =            Qc ,   ^1.15     4 ^{. (6)}

P s ^- P w   V gh v )

Таким образом, все полученные формулы расхода взвешенных и влекомых наносов и транспортирующей способности потока основаны на уравнении движения воды и твердого вещества, концепции фазового гидравлического пространства и соотношений, описывающих критические состояния потока. Все приведенные выше формулы были апробированы на водотоках разной физико-географической принадлежности и показали хорошие результаты.

ЗАКЛЮЧЕНИЕ

Существующие методы расчета транспорта наносов не всегда являются универсальными и подходят для потоков любого масштаба и разных гидравлических условий. При этом процесс транспорта наносов в любой форме (взвешенной или влекомой) и любой степени насыщения твердой фазой потока (от осветленной до транспортирующей способности) един для всех типов русел для любого периода водности. В основе этого процесса лежит энергия речного потока, определяющая массу транспортируемого твердого вещества. В соответствии с этим, алгоритмы оценки расхода наносов любой формы должны явиться следствием теоретических уравнений, описывающих гидродинамику двухфазного речного потока. Это означает, что эти алгоритмы (расчетные формулы) должны быть полностью взаимосвязаны между собой, вытекать один из другого. А структура формул транспорта наносов должна быть полностью скоординирована с возможностями измерительной базы. В частности, крайне изменчивая в поперечном сечении потока величина средней крупности донных отложений или ее квантильные значения заданной обеспеченности снижают точность вычислений. Более удобно в этом случае оперировать интегральными характеристиками русла, такими как категории крупности донных отложений. Приведенные в данной работе алгоритмы в целом позволяют избежать обозначенных выше недостатков и повысить точность расчетов расхода наносов для разных типов рек.

Представленная в данной работе методология решения геоэкологических задач, связанных с оценкой твердого стока водных объектов, основана на принципах взаимодействия и взаимовлияния гидравлических переменных состояния и твердого вещества в водном объекте. Следствием этих принципов являются взаимосвязанный расчет гидравлических переменных состояния потока и твердого вещества, динамическое в отношении донного грунта представление взаимодействия потока и дна, концепция фазового гидравлического пространства. На этих принципах основаны разработанные взаимосвязанные детерминированные и стохастические методы и модели. Система этих методов и моделей характеризуется физически обоснованными параметрами и пригодна для водных объектов разной физико-географической принадлежности с любой формой транспорта твердого вещества (взвешенной или влекомой). Перспективы развития данной методологии направлены в первую очередь на совершенствование и расширение методов оценки твердого стока. В том числе, в качестве одного из ориентиров дальнейшего развития – разработка концепции и методов расчета вторичного загрязнения водных объектов через инициацию процессов взмучивания и транспорта донных отложений.