Geometric Invariant Robust Image Hashing Via Zernike Moment
Автор: Rui Sun, Xiaoxing Yan, Wenjun Zeng
Журнал: International Journal of Wireless and Microwave Technologies(IJWMT) @ijwmt
Статья в выпуске: 5 Vol.1, 2011 года.
Бесплатный доступ
Robust image hashing methods require the robustness to content preserving processing and geometric transform. Zernike moment is a local image feature descriptor whose magnitude components are rotationally invariant and most suitable for image hashing application. In this paper, we proposed Geometric invariant robust image hashing via zernike momment. Normalized zernike moments of an image are used as the intermediate hash. Rotation invariance is achieved by taking the magnitude of the zernike moments. Image normalization method is used for scale and translation invariance. A randomization diffusion processing enhance hashing security. The test results show that our method is robust with respect to the geometrical distortions and content preserving processing.
Zernike moment, Geometric invariant, image hashing , image indexing, robustness
Короткий адрес: https://sciup.org/15012759
IDR: 15012759
Текст научной статьи Geometric Invariant Robust Image Hashing Via Zernike Moment
Because of the easy-to-copy nature, tremendous growth and wide spread of multimedia data have led to an urgent, challenging research issue: How to efficiently manage such abundant data (e.g. fast media searching, indexing and identification) and provide sufficient protection of intellectual property as well? Among the variety of techniques, image hashing, which is a content-based compact representation of an image [1], has been proved to be an efficient tool because of its robustness and security.
An Image hash function maps an image to a short binary string based on the image’s appearance to the human eye. It finds applications in image authentication, digital watermarking, and content-based image retrieval (CBIR). In particular, a perceptual image hash function should have the property that two images that look the same to the human eye map to the same hash value, even if the images have different digital representations. This differentiates a perceptual hash from traditional cryptographic hashes, such as SHA-1 and MD-5. SHA-1 and MD-5 hashes are extremely sensitive to the input data. On the other hand, image may be tampered by
* Corresponding author.
malicious attackers. Unacceptable changes should produce a completely different hash. In general, an ideal image hash should have the following desirable properties:
Perceptual robustness: The hash function should map visually identical images to the same hash even if their digital representations are not exactly the same. Visually similar images without significant differences may have hashes with a small distance.
Uniqueness: Probability of two different images having an identical hash value, or very close hash values, should tend to zero.
Sensitivity to visual distinction: Perceptually important changes to an image should lead to a completely different hash. This feature is essential for the image hash to be useful in image authentication and digital forensics.
In recent years, Much attention has been concentrated on the robustness of image hashing against geometric transformation, specifically, rotation, scaling, and translation (RST attacks). An algorithm called RAdon Soft Hash (RASH) was proposed using the properties of the Radon transform [2]. The first 40 DCT coefficients of the RAV vectors are used to construct the image hash. Since the hash is based on radial projections, it is resilient to scaling and rotation. In [3], it uses the Radon coefficients on one projection (one direction) to generate the image hash. However, none of them introduce a key to ensure source authentication of image. In [4], Swaminathan, et al. propose an image hashing scheme in which they exploit the properties of discrete polar Fourier transform to make the hash resilient to geometric and filtering operations, and incorporate keys into the hash to achieve security against guessing and forgery. Monga[5] propose to use nonnegative matrix factorization (NMF) for robust image hashing. geometric attacks on images correspond to iid noise on NMF vectors, it is very useful to uncorrelate the affect of geometric attacks. Those methods have advantages in robustness and security. However, it does not mean that the robustness has not been solved very well.
In this paper, our work focuses on developing a robust method against geometric attacks and has good Sensitivity meanwhile. Zernike moments have been shown to be superior to the others in terms of their insensitivity to image noise, information content, and ability to provide faithful image representation [6]. We achieved the rotational invariance from the property of the Zernike moment and scale and translation invariance by normalization.
-
2. Zernike Moments
Zernike moments (ZMs) have been used in object recognition, image watermarking and image analysis regardless of variations in position, size and orientation [7] [8]. Basically, the Zernike moments are the extension xmyn of the geometric moments by replacing the conventional transform kernel with orthogonal Zernike polynomials. The relationships between the Zernike moments and geometric moments can be established [39]. The ZM coefficients are the outputs of the expansion of an image function into a complete orthogonal set of complex basis functions nm™(p, ^)i. Teh and Chin [6] show that among many moment-based shape descriptors, Zernike moment magnitude components are rotationally invariant and most suitable for shape description.
The Zernike basis function with order and repetition is defined over a unit circle in the polar coordinates as follows:
-
V. W = R- ( P)e' " for P S 1
Where { R ( p )} is a radial polynomial in the form of
( n -| m\ /2
s !
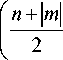
( n - 5 )! _____________ n - 2 5
X ( I A p i| n - m i
- 5 !---u- 5 !
Л 2 J
R nm ( P ) = Z ( — 1) $
5 = 0
Here, n is a non-negative integer and m is an integer satisfying the conditions: n — |m | is even and| m | < n . The set of basis functions { V m( p , 0 ) } is orthogonal, i.e.
withS^
1,
0,
2 n 1
J J ' • (p, OVpq (p, 0) pdpdO = П 5ir5mq
'0« n + 1
a = b
otherwise
The 2-D ZMs for a continuous image function f ( p , O') are represented by
+ 1 2 ” 1
Z.m = n— f f f (p-0)Vm (p,0) pdpdO n ".
For a digital image function, the 2-D ZMs are given as
Z,„ = n + ' ZZf (p,0)Vnm (p,0)
П ( p , 0 ) e unitdisc
The Zernike moments can be viewed as the responses of the image function f ( p , 0 ) to a set of quadraturepair filters { V nm ( p , 5 ) } .
The proposed method extract firstly RST invariant feature via normalized zernike moment procedures.
A. Normalized Zernike Moment
Consider a rotation of the image through angle a . If the rotated image is denoted by f , the
relationshipbetween the original and rotated images in the same polar coordinate is
f '(p,0) = f (p,0— a)
It can be shown that the Zernike moments Zn of the rotated image f ' ( p , O') become, Z nm = Z nm exp( — jm a )
Equation (7) shows that each Zernike moment acquires a phase shift on rotation. Thus, Z ' , the magnitude of the Zernike moment, can be used as a rotation-invariant feature of the image.
Scale and translation invariance can be achieved by utilizing the image normalization technique as shown in
f (x, y)
[9]. An image function , can be normalized with respect to scale and translation by transforming it into
g ( x , y ), where
I X У I
g(x, У) = f I - + x - + У I
V a a )
with ( X , y ) being the centroid of f ( X , y ) and a = p / m^ order moment.
,with в a predetermined value and m 00 its zero-
It has been proved that an image and its affine transforms have the same normalized image. See the example in Fig 1. Hence, we first move the origin of the image into the centroid and scale it to a standard size. If we compute the Zernike moments of the image, then the magnitudes of the moments are RST invariant.

(a) (b) (c)
Fig1. (a) Original man image. (b) Man image in (a) after distortion. (c) Normalized image from both (a) and (b).
-
B. The Proposed method
-
(1) The method takes a test image i ( x , y ) and normalize it into a standard image i ( x , y ) for scale and translation compensation. Zernike moments Zn of the normalize image are computed. A feature vector p is constructed with the Zernike moments of the test image as
p = [ p 1 , p 2 ,'**, p N ] = [I A 20 , A 22! , ™! A N max N maxi ]
where N is the length of the feature vector and N is on the order of Zernike moments.
-
(2) Generally, the length of the feature vector is short , if the attacker know the hashing method he can estimate or forgery hash. We need the randomization processing to diffusion the feature vector. Regulate the each coefficients of the feature vector to 0~1. Choose randomly M sub sequence {lt , l 2, " , lM } from feature vector p .The length of each sub sequence is k , M >> N , k < N /2 .The procedure enlarge the difference of images and enhance the security and the distinguish ability.
-
(3) Generate pseudorandom weight vectors {t }, i = 1, " M
The resulting vector of length M is given by
H = {(l1, t 1), l2 2, t 2 ),' " (lM , tM )} where a,b denotes the inner product of vectors a andb .
-
(4) The final hash is built using quantization and a binary hash string.
-
4. Experimental Results
In this section, the proposed scheme is evaluated by performing various experiments on different images. The standard testing images (including Lena, Barbara, Peppers, Baboon, Bridge and Man) and a nature image database [10] is used. All images are cropped to 256 x 256 and converted into 8-bit gray-scale. The parameters used for the method are N = 14 , M = 30 , k = 7 . The coefficients of vector H are quantized and represented by 6-bit binary strings. Therefore, our final hash is 180 bits length. We use Normalized Hamming Distance (NHD) to measure the similarity of hashes, which is defined as follows.
L
NHD (h 1, h2) = 12| hl - h,\
L i = 1 (9)
Where L is the length of the hash. If the distance between two hashes is greater than a threshold T , two images are considered different. Otherwise they are similar.
-
C. Perceptual Robustness
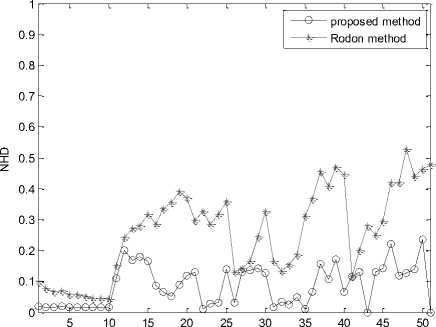
We firstly test the robust capability of the proposed scheme. Specifically, given an original image, we generate 51 similar versions by manipulating the original image according to a set of content preserving operations (CPOs) listed in Table 1. Fig. 2 and Fig. 3 depict the similarity performance of the lena and man by comparing our proposed scheme with the Radon-DWT scheme[3] under various CPOs. The x axis denotes the image indices shown in Table 1. Obviously, our scheme performs more robust results than Radon-DWT scheme especially under geometric attacks.
Table1. Types and parameters of CPOs
|
CPOs |
parameters |
Image indices |
|
JPEG compression |
QF:10:10:100 |
1-10 |
|
Gaussian noise |
Variance 0.01:0.01:0.05 |
11-15 |
|
Median filter |
Mask size 2:1:6 |
16-20 |
|
Average filter |
Mask size 2:1:6 |
21-25 |
|
Wiener filter |
Mask size 2:1:6 |
26-30 |
|
rotation |
Degree -2,-1, 1, 2, 5,10,15,30,45,90 |
31-40 |
|
scaling |
Percentage 0.7:0.2:1.5 |
41-45 |
|
shearing |
Percentage 0.01:0.01:0.05 |
46-50 |
|
mirror |
-- |
51 |
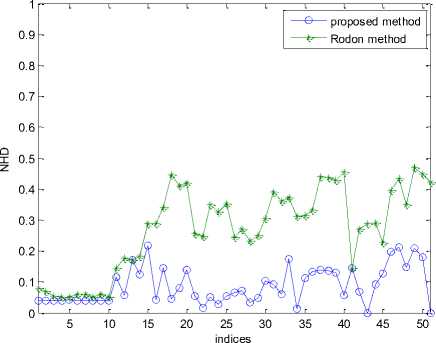
Fig. 2. Robust testing under CPOs on Lena image
indices
Fig. 3. Robust testing under CPOs on Man image
-
D. Discriminative Capabilities
0.9
0.8
0.7
0.6
0.4
0.3
0.2
0.1
Here we evaluate the discriminative capability to different images of our scheme. Firstly we calculate the normalized Hamming distance between standard testing images. we compare the Lena image with other five images separately. The results is shown in Fig. 4. While comparing with the Radon-DWT scheme, we observe that our scheme achieves a higher Hamming distance, which means our scheme has a higher discriminative capability. Secondly, we test the false acceptance probability. The hamming distances are calculated between Lena and 500 natural images which are randomly selected from the database [10]. Here we aim to justify whether the scheme can distinguish the same and different images. In image hashing, we define a threshold T, where if the Hamming distance is less than T, the two images are regarded as perceptual similar or the same. Therefore, given the 500 hashes which are generated from totally two different images, we record the number of the distances which are less than T. A comparison of the false acceptable probabilities between our scheme and Radon-DWT scheme are shown in Table 2. Obviously our scheme has a very lower false acceptable probability than Radon-DWT scheme, i.e. the collision rate of our scheme is lower.
^е proposed method । । Rodon method
I II II II II
Bridge
Baboon
Barbara
Man
Peppers
Fig 4. The normalized Hamming distance between Lena and the other five test images
Table 2 False Acceptance Rate
|
Threshold |
0.2 |
0.25 |
0.3 |
0.35 |
0.4 |
|
Proposed |
0.001 |
0.008 |
0.05 |
0.12 |
0.23 |
|
Rodon |
0.012 |
0.06 |
0.16 |
0.29 |
0.45 |
In this paper, we have proposed geometric invariance image hashing scheme by normalization zernike moment. Zernike moments are used for the rotation invariant hashing. With the combination of normalization, we have achieved RST invariance. Our proposed scheme is simple but has a prominent simulation results than the existing scheme. We use random diffusion processing and pseudorandom weight vectors to generate randomness and provide security of image hashing. Furthermore, the experimental results showed that our proposed scheme achieves robustness performance for content preserving operations, and also a satisfactory discriminative capability performance. The further work will focus on theoretical security analysis.
This work is supported by the National Natural Science Foundation of China (Project Number: 61001201), the College Young Foundation of Anhui Province (Project Number.2009sqrz013zd).
-
[1] V.Monga, Pe rceptually based methods for robust image hashing, Ph.D thesis, University of Texas, 2005.
-
[2] C.D.Roover, C.D.Vleeschouwer, F.Lefebvre, and B.Macq, “Robust image hashing based on radial variance of pixels,” in IEEE International Conference on Image Processing (ICIP’05), 2005, pp. 77–80
-
[3] X.C.Guo and D.Hatzinakos, “Content based image hashing via wavelet and radon transform,” in PCM 2007, 2007, LNCS 4810, pp. 755–764.
-
[4] A. Swaminathan, Y. Mao, and M. Wu, Robust and secure image hashing, IEEE Transactions on Information Forensics and Security, vol. 1, no. 2, 2006, pp. 215-230.
-
[5] V. Monga and M. K. Mihcak, Robust and secure image hashing via non-negative matrix factorizations, IEEE Transactions on Information Forensics and Security, vol. 2, no. 3, 2007, pp. 376-390.
-
[6] C. H. Teh and R. T. Chin, “On image analysis by the methods of moments,” IEEE Trans. Pattern Anal. Machine Intell., vol. 10, pp. 496–513, Apr. 1988.
-
[7] B. S. Manjunath, J.-R. Ohm, V. V. Vasudevan, and A. Yamada, “Color and texture descriptors,” IEEE Trans. Circuits Syst. Video Technol., vol. 11, no. 6, pp. 703–715, Jun. 2001
-
[8] H. S Kim, H. K Lee. Invariant image watermark using Zernike moments. IEEE Trans. Circ. Syst. Video Tech. 13, 8, 766—775, 2003
-
[9] P. Dong, J.G. Brankov, N.P. Galatsanos, Y. Yang, and F. Davoine,"Digital Watermarking Robust to Geometric Distortions," IEEE Trans. Image Processing, Vol. 14, No. 12, pp. 2140-2150, 2005
-
[10] http://cvcl.mit.edu/database.htm
Список литературы Geometric Invariant Robust Image Hashing Via Zernike Moment
- V.Monga, Perceptually based methods for robust image hashing, Ph.D thesis, University of Texas, 2005.
- C.D.Roover, C.D.Vleeschouwer, F.Lefebvre, and B.Macq, "Robust image hashing based on radial variance of pixels," in IEEE International Conference on Image Processing (ICIP'05), 2005, pp. 77–80
- X.C.Guo and D.Hatzinakos, "Content based image hashing via wavelet and radon transform," in PCM 2007, 2007, LNCS 4810, pp. 755–764.
- A. Swaminathan, Y. Mao, and M. Wu, Robust and secure image hashing, IEEE Transactions on Information Forensics and Security, vol. 1, no. 2, 2006, pp. 215-230.
- V. Monga and M. K. Mihcak, Robust and secure image hashing via non-negative matrix factorizations, IEEE Transactions on Information Forensics and Security, vol. 2, no. 3, 2007, pp. 376-390.
- C. H. Teh and R. T. Chin, "On image analysis by the methods of moments," IEEE Trans. Pattern Anal. Machine Intell., vol. 10, pp. 496–513, Apr. 1988.
- B. S. Manjunath, J.-R. Ohm, V. V. Vasudevan, and A. Yamada, "Color and texture descriptors," IEEE Trans. Circuits Syst. Video Technol., vol. 11, no. 6, pp. 703–715, Jun. 2001
- H. S Kim, H. K Lee. Invariant image watermark using Zernike moments. IEEE Trans. Circ. Syst. Video Tech. 13, 8, 766—775, 2003
- P. Dong, J.G. Brankov, N.P. Galatsanos, Y. Yang, and F. Davoine,"Digital Watermarking Robust to Geometric Distortions," IEEE Trans. Image Processing, Vol. 14, No. 12, pp. 2140-2150, 2005
- http://cvcl.mit.edu/database.htm


