Geometric patterns of the Konya Sultanate

The art of Islamic geometrical ornamentation supposedly originated in the second half of the 10th century in the Samanid empire with its capital in Bukhara, and developed over the next two centuries on the vast territory from Transoxiana, Khora-san and Afghanistan in the east to Azerbaijan and Persian Iraq in the west. Geometric patterns of this art are composed of broken lines dividing the plane into polygons; the result has a rich set of symmetries, which turn the pattern into itself by translations, rotations and mirror reflections. In Farsi, such a pattern is called girih, which means “knot”; this is especially emphasized when broken lines turn into ribbons intertwining with each other. The invention and construction of such patterns presupposes a good knowledge of geometry, and educated geometers of that era certainly put their minds into this matter.

In the Konya Sultanate, located in Asia Minor, the decoration of buildings with geometric patterns begins in the first decade of the 13th century and continues throughout the whole of that century. The Konya Sultanate is a Seljuk Turkic state that arose in the late 11th century in Anatolia, with capital in Konya. The Turks who came to Asia Minor spoke their native language, while the language of court and culture was Persian, the language of religion was Arabic, and the inhabitants of this

land also spoke Greek, Armenian and other languages of Asia Minor. The Konya Sultanate reached its heyday in the first half of the 13th century, when the countries to the east of it had already been captured by the Mongols. The Kösedağ battle with the Mongols took place in 1242 and was lost, after which the Konya Sultanate fell into vassal dependence on the Mongol khans, although it was not completely conquered by them. From that time it began to decline, however, in the field of culture flourished for another half century, and by the end of the 13th century it broke up into the possessions of individual rulers. One of these possessions in western Anatolia became later the origin of the Ottoman Empire.

The flourishing of ornamental art in 13th-century Anatolia can be explained by several factors. Firstly, this includes the flourishing of the Seljuk state itself, located on important trade routes; its rulers contributed to this trade in every possible way, as evidenced by the quantity and quality of the numerous caravanserais; the construction of mosques and madrasahs was there as intense too. Secondly, this is the escape of the inhabitants of the east lands to Asia Minor, caused by the Mongol invasion. Among those who fled to the west from the horrors of this invasion there were masters of architecture who brought with them the secrets of their art. They had something to offer to the rulers, and the rulers had the means to implement this offer. As a result, the art of geometric decoration experienced a new round of its heyday, while in the devastated east it fell into decline and was revived only towards the end of the 14th century in the Timurid Empire.

Another factor due to which a large number of monuments from the 13th century have survived to this day, in comparison with the few monuments of the two previous centuries, is that in the Konya Sultanate the construction of significant buildings was carried out mostly from stone. Everything that was built in Khorasan from raw bricks dissolved and become clay; buildings made of baked bricks without maintenance also quickly collapse under the weather conditions, but a stone structure still stands today, unless it was destroyed by an earthquake or its blocks were used for some other construction. At the same time, the freestones used in decoration are easily processed, so it was possible to produce a lot of carved decorations in a relatively short time. The skill of stone processing, accumulated over centuries by Greeks, Armenians, and other former inhabitants of Asia Minor, also had an impact in this art.

In addition to stone carving, geometric decorations in mosques and madrasahs of the Koniya Sultanate were also made using a new technique of kashi mosaic. Such mosaic was usually made with cut tiles of two colors: turquoise and aubergine purple. The joints of the tiles, and sometimes some free spaces between them, were coated with white mortar. In some cases, the stucco carving or molding technique developed by masters of previous centuries was also used.

The Seljuk buildings that have survived to this day in Anatolia are mosques, madrasahs, caravanserais, hospitals, baths, mausoleums, bridges. The local mosques (cami), in comparison with later mosques of the Ottoman Empire, are small and unassuming in appearance. They are designed for cold winters and always have a roof supported by wooden or stone columns. From the outside, the mosque is surrounded by a solid stone wall, devoid of any decorations; against this background, the entrance portal with rich ornamental decor of border stripes and stalactite muqarnas stands out. Inside the mosque, the mihrab, a niche showing the direction to Mecca for the prayers, is decorated in a similar way. The mimbar, a pulpit for Friday sermons, is decorated with wood carvings. Excellent examples of such complete decoration are Alaeddin Mosque in Konya, Eşrefoglu Mosque in Beyşehir, Arslanhane Mosque in Ankara, etc.

The madrasah, which is a learning institution, has a courtyard with hujras (students’ rooms) opening into it, some classrooms and vaulted iwans. Depending on the size of the madrasah, this courtyard could be open from above or covered with a dome. In a madrasah, in addition to the entrance portal, the iwan and the dome can also be richly decorated; the best example of such a decor is Karatay Madrasah in Konya.

A caravanserai (han), a roadside inn, is a solid structure with an open courtyard and a covered rear hall. The building is surrounded by strong walls, which protect travelers from bad weather and robbers. Caravanserais, separated from each other by a day’s march, formed a network, which made travel on trade and other business a very pleasant experience. The external entrance to the courtyard and the internal entrance to the rear hall usually have stone-carved decoration.

The typical Seljuk mausoleum (türbe) was built according to the same scheme as in western Iran: there is octagonal or decagonal tower with a double dome, a spherical inner one and a conical outer one. The ornamental decoration of Seljuk mausoleums was quite modest in comparison with the mausoleums of Maragha and Nakhichevan, entirely covered with geometric patterns.

As for the palaces of the rulers of the Konya Sultanate, not one of them has survived to this day, and all our information about them is based on the results of archaeological excavations.

The number of geometric patterns from the Konya Sultanate that have survived to this day is huge, which makes them an invaluable monument to this branch of art, combining aesthetics with geometry. It would be very plausible to assume that a significant part of these patterns was invented earlier: after all, we see many its ideas and implementations in the surviving buildings and the finds of archaeological expeditions of Transoxiana, Iran and Afghanistan. Since very few of the ornamented monuments of the 11th–12th centuries have reached our days, the ornaments of Konya, Kayseri, Sivas, Niğde, Malatya, Isparta, Beyşehir and other cities of Anatolia represent not only themselves, but also a large extent art of previous centuries. On the other hand, many new motifs were invented there in 13th century, which we also will discuss below.

Dating

The exact dating of architectural ornaments usually is based on the building inscriptions which indicate the year of construction, with the name of the person who financed the building or the person buried in the mausoleum, and sometimes, the name of the architect. However, such an inscription indicates the year when construction began or the year of death of the buried person, not the year when the building was completed. This creates a certain shift in time dating.

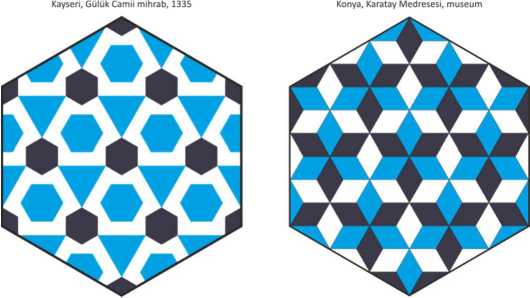
Such a shift can be especially significant for the mihrabs, decorated with glazed colored ceramics. For example, Gülük Mosque in Kayseri was built in the 12th century, renovated in 1210, as evidenced the inscription on its corner portal, and renovated again in 1335. This mosque has a ceramic mihrab, distinguished by its size and colored ornamentation, unusual for Kayseri. The technique and style of its execution are typical of many mihrabs of the 13th century. Unfortunately, the lower part of the mihrab was badly damaged, and its tile patterns were restored only conditionally, using painting on plaster. The pattern on the side walls of its niche also adorns the stone portals of Momine Hatun (1338) and Hoca Kiliç (1249) mosques in Kayseri (Fig. 1). Therefore, this mihrab can be assumedly dated to the second half of the 13th century, without any reference to the known dates of repair.

Momine Hatun Camii

Giiliik Cami

Носа Kilis Camii

Fig. 1. Patterns from Gülük, Momine Hatun and Hoca Kiliç mosques in Kayseri.

It was possible to move a glazed mihrab from one place to another carefully piece by piece. The example is Misri Mosque in Afyon. The mosque itself was built in 1483, but its mihrab evidently was created two centuries earlier. It is possible that it was originally located in a fortress mosque on top of a cliff overlooking the city, and was moved from there when the fortress fell into disrepair.

Another example is the ornamentation of the mihrab in the Piri Mehmet Paşa Mosque in Konya, built in 1523. It is completely covered with gold paint, but its geometry is related to some other patterns of 13th century (Fig. 2), which leads to the assumption that this mihrab was transferred here from some earlier mosque in Konya.

Piri Mehmet Paja Camii

Fig. 2. Detail of mihrab from Piri Mehmet Paşa mosque in Konya.

In general, the earliest ornaments of the Konya Sultanate are located on buildings of the first two decades of the 12th century. Earlier buildings, such as monumental stone Friday mosques in Sivas (1197, repaired 1212) and Kayseri (12th century, repaired 1206), or Iplikçi Mosque in Konya (1201), are completely devoid of ornamental decoration of the portals, so it seems that at that time it was still unknown here. Therefore, the appearance of the art of geometric ornamentation in the Konya Sultanate can be quite confidently associated with the arrival of outstanding masters of this art from Khorasan and Azerbaijan. A number of very sophisticated ornaments from the Konya Sultanate are also known from some sites in Khorasan, as excavations of the palace of Termez rulers (Shchetnikov 2024), and from the mausoleums of Maragha and Nakhichevan (Cromwell 2018), dated to the end of 12th century. Of course, such patterns got to the Konya Sultanate through the chain of tradition and were not rediscovered.

The decline of the Seljuk state, which disintegrated into separate beyliks, wars with neighbors and among themselves did not contribute to the flourishing of architecture and architectural ornament. This art died out in Anatolia it the first half of the 14th century. Later, this tradition again returned to Khorasan and flourished in the Timurid state, but in a different appearance, with turquoise portals and domes characteristic of this new style.

Technical notes

I will classify the patterns, firstly, according to the wallpaper groups (see the list of 17 wallpaper groups in Schattschneider 1978), and secondly, according to characteristics of their similarities, so that they form homological series. Defining the wallpaper groups, I do not pay attention to the interlacing of ribbons, which breaks the mirror symmetry, turning the group p6m into p6, p4m into p4 and so on.

Many patterns are represented in situ by a narrow border strip or other fragment. Drawing the pattern, I restore its geometric design to the integrity, returning to the original geometric idea behind the implementation.

The same pattern can be rotated differently relative to the vertical axis. I try to bring all the patterns to one orientation for the purposes of their analysis and comparison, and do not indicate how they are orientated in situ.

The mosaic patterns I redraw in color, trying to match the colors to the original. The patterns carved in stone I redraw in light and dark brown.

If some pattern is found in the Konya Sultanate more than once, I usually indicate only one of its locations. I have not the goal of creating a complete catalog of all patterns found there, although the below collection is quite extensive and representative. I relied primarily on excellent three-volume review of Seljuk architecture written by Ziya Kenan Bilici (2016), on a number of websites dedicated to this architecture, on numerous photographs by various authors from Facebook and Google Maps, and on my own observations and photographs taken in Turkey. Among the reviews of Islamic patterns, I would first of all recommend the database and the fundamental research of Jay Bonner (2017). Some other useful books and papers are listed in the bibliography.

Wallpaper group p6m

In this section, we consider patterns of the p6m wallpaper group. The number 6 shows that these patterns have 6-fold rotational symmetry; the letter m indicates their mirror symmetry. Such patterns are built on hexagonal lattice (Fig. 3). The centers of 6-, 3- and 2-fold symmetry are marked here with red circles, green triangles and blue rhombuses respectively. Two families of mirror symmetry axes are shown in red and blue dash-dotted lines.

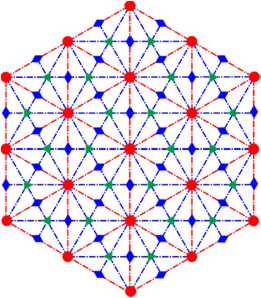
Fig. 3. Lattice of p6m group.

The simplest patterns of the p6m group are shown in Fig.4. Such patterns usually decorate muqarnas, the vaulted honeycombs on the mihrab.

Elazig, Harput Arap Baba Mescidi, 1279

Beyjehir, Ejrefoglu Camii, 1296

Malatya, Ulu Camii, 1247

Afyon, Misri Camii (1483)

Afyon, Misri Camii (1483)

Malatya, Ulu Cami, 1247

Fig.4. Simple patterns of p6m group.

The next series (Fig.5) represents simple patterns created by interlacing ribbons. Note that in the second pattern some 6-pointed stars are surrounded by six hexagons, and these are 6-fold centers; and some 6-pointed stars are surrounded by three hexagons and three rhombuses between them, and these are 3-fold centers.

Fig.5. Simple patterns created with ribbons.

The ribbons in next six patterns (Fig.6) have the form of regular hexagons. These hexagons may be of one size (first three patterns) or of two different sizes. The last pattern of this series also contains regular dodecagons.

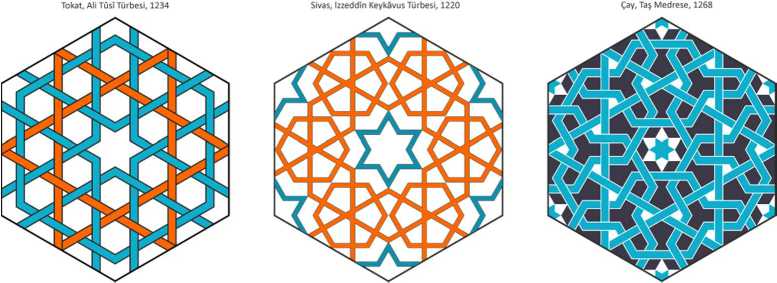
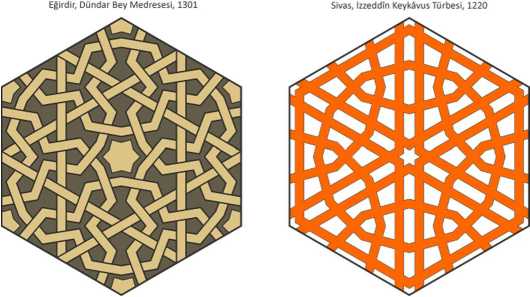
Fig.6. Patterns with interlacing hexagons.

The next three patterns (Fig.7) have common basic structure. Between two 6-pointed stars in 6-fold centers there are the jugs in 2-fold centers; between three adjacent jugs there is a trefoil in 3-fold center. The first pattern is outlined by contour lines; two others are drawn with interlacing ribbons, closing by different ways.

Elazig, Harput Arap Baba Mescidi, 1279                                   Konya, Sirrah Medrese, 1242                                     Sivas, fifte Minardi Medrese, 1271

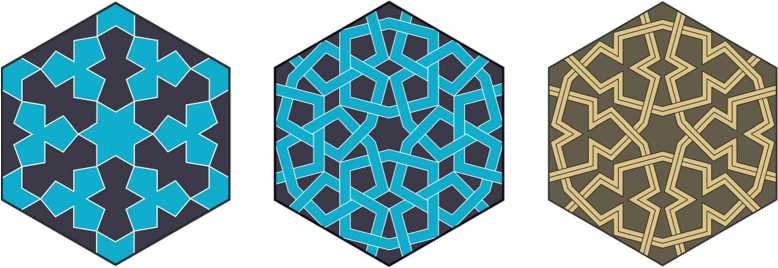
Fig.7. Patterns with 6-pointed stars, jugs and trefoils.

The first two patterns in Fig.8 have common basic structure, where a 6-pointed star is surrounded by six T-shaped figures, which form triplets around 3-fold centers. This pattern has become widespread, extending beyond the borders of the Islamic world; its earliest known version adorns the eastern Kharraqan tower (1068). In the third pattern, a 6-pointed star also is surrounded by T-shaped figures, but now these figures form doublets around 2-fold centers, and their crossbars are “pressed” by the vertices of big hexagons.

Akjehir, Kileci Mescidi, c. 1235                                      Kayseri, Haci Kilif Camii, 1249                                      Konya, Alaeddin Camii, c. 1235

Fig.8. Patterns with 6-pointed stars and T-shaped figures.

The peculiarity of the following patterns (Fig.9) is that their p6m structure contains regular pentagons. This idea comes from 12th century Khorasan; the earliest known pattern of this kind was situated on the peshtak in Abiwerd. The first two patterns are identical to each other, differing only in the proportions of their parts. In their 6-, 3- and 2-fold centers there are 6-pointed stars, regular triangles and common vertices of twin pentagons respectively.

Konya, AlaeddTn Camii, c. 1235                                     Konya, Sirgah Medrese, 1242                                      Akjehir, Alaeddin Camii, c. 1235

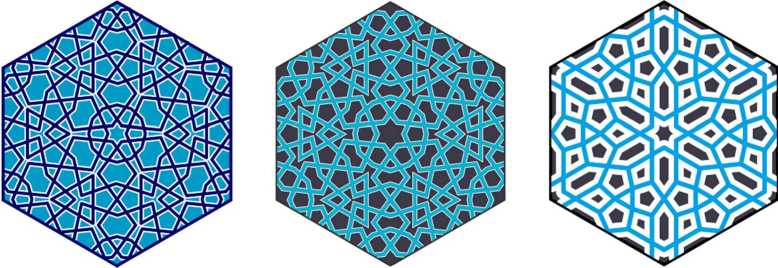
Fig.9. Patterns with 6-pointed stars and regular pentagons.

Now let’s turn to patterns with 12-pointed stars at 6-fold centers. The first pattern in Fig.10 can be obtained connecting 12-pointed stars with their vertices and adding small triangles between them. This pattern has a long history; its first known example decorates the eastern Kharraqan tower (1068). The lines of the second pattern are slightly deformed to make the pentagons closer to regular ones. The stars in the third pattern are moved away from each other, so that the jugs are located between them.

Fig.10. Patterns with 12-pointed stars.

Three following patterns (Fig.11) consist of 12-pointed stars, connected by a “glue” of slightly irregular 5-pointed stars. The 12-pointed stars look at each other with their rays in the first pattern, and with the spaces between their rays in other two patterns.

Kayseri, Haci K1I15 Camii, 1249 Aksaray, Cincikli Mescid, c. 1250

Fig.11. Patterns with 12- and 5-pointed stars.

In the next series (Fig.12), regular 6-pointed or 12-pointed stars are located in 6-fold centers, and regular nonagons or 9-pointed stars are located in 3-fold centers.

Ankara, ArslanhSne Camii, 1289

Sivas, Buruciye Medresesi, 1271

Konya, Alaeddin Camii, c. 1235

Konya-Aksaray, Sultan Hani, 1229                                    Konya, Alaeddin Camii, c. 1235                                  Aksaray-Nevjehir, Agzikara Han, 1231

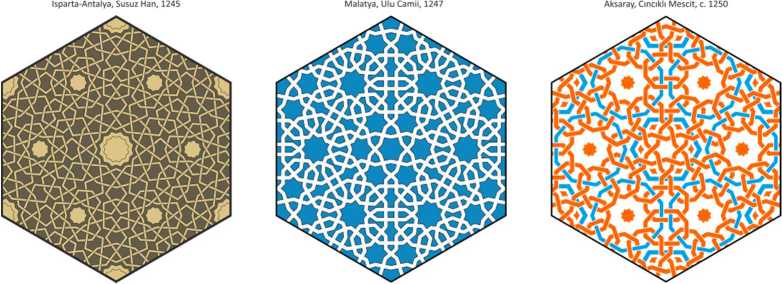
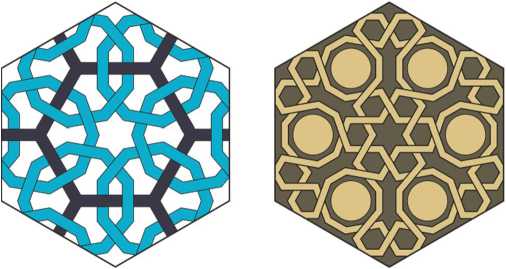
Fig.12. Patterns with nonagons or 9-pointed stars in 3-fold centers.

The next three patterns have squares in 2-fold centers (Fig.13). In the first and second patterns the 6- or 12-pointed star in 6-fold center receives an elegant frame of six squares; triplets of these squares touch at their vertices at 3-fold centers. The basic structure of the third pattern is a plane tessellation of regular hexagons, squares and equilateral triangles; this basic structure also could be considered as the overlap of regular dodecagons.

Sivas, Buruciye Medresesi, 1271                                   Qemijgezek, Yelmaniye Camii, 1404                                    Sivas, Jitaiye Medresesi, 1217

Fig.13. Patterns with 6- or 12-pointed stars and squares.

The next patterns have 6-pointed stars in 6-fold centers and regular octagons in 2fold centers (Fig.14). The interesting detail of the first pattern is that the triplets of octagonal ribbons form Borromean rings, which are not linked pairwise, and the non-unlocked weave occurs due to the third ring of the triplet.

Kir$ehir, Caca Bey Medresesi, 1272                                    Aksaray, Cincikli Mescit, c. 1250                                      Konya, Alaeddin Camii, c. 1235

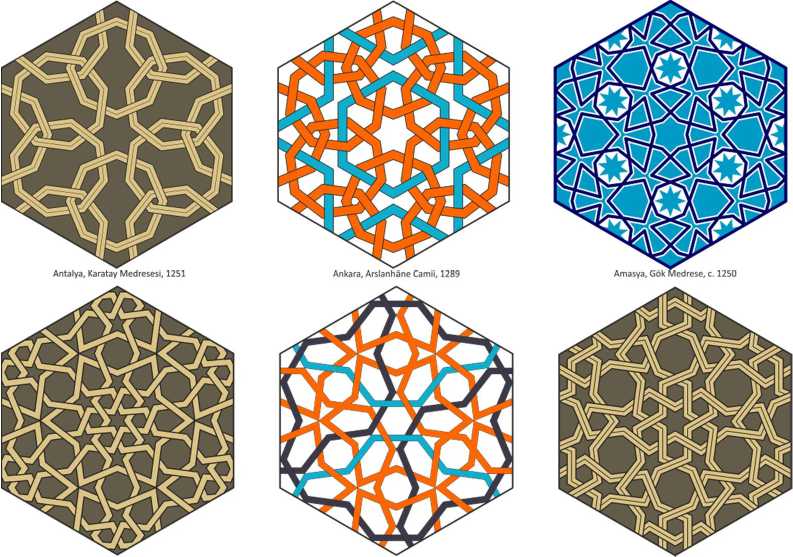
Fig.14. Patterns with 6-pointed stars and octagons.

In the next two patterns (Fig.15), the symmetry order of regular stars and polygons increases. In both patterns, there are 12-pointed stars in 6-fold centers. In the first pattern, also there are 6-pointed stars in 3-fold centers, and 4-pointed stars in 2- fold centers. In the second pattern, there are nonagons in 3-fold centers, surrounded by three slightly irregular heptagons, and 8-pointed stars are in 2-fold centers. The third pattern consists of 12-pointed stars in 6-fold centers, hexagons in 3fold centers and non-perfect 10-pointed stars in 2-fold centers.

Ahlat, Selguklu Mezarhgi                                            Ahlat, Selguklu Mezarhgi                                              Van, Ulu Camii, 13 c.

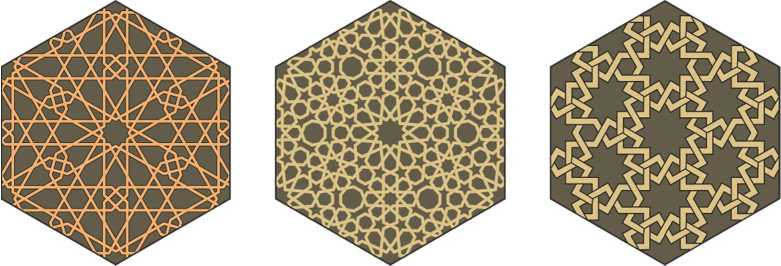
Fig.15. Patterns with 12-pointed stars.

In the next pattern, 12-, 9-, 10-pointed stars are connected with 6-, 3-, 2-fold centers respectively (Fig.16). In addition, this pattern contains 11-pointed stars, which are not tied to any centers of symmetry. The choice of 11-pointed stars in this design is associated with one interesting mathematical fact. Let’s calculate the sum of the angles in the green triangle. Here 10-pointed star gives 1/5, 12-pointed star gives 1/6, and 11-pointed star gives 7/11 of a straight angle. However, the sum 1/5+1/6+7/11=331/330, which differs from 1 by 1/330. This paradox is resolved by the fact that the rays coming from the centers of 10- and 11-pointed stars towards each other do not lie on the same straight line, so the corresponding side of the green “triangle” is broken.

Avanos, Sari Han, 1218

Fig.16. Pattern with 12-, 11-, 10-, 9-pointed stars.

We finish the analysis of the p6m group with two patterns, which have 24-pointed stars in their 6-fold centers (Fig.17). The first design also contains regular 12- and 8-pointed stars in 3- and 2-fold centers, with small irregular 5-pointed stars as a “glue”. The structure of the second pattern is more tricky. Each 24-pointed star is surrounded by 24 irregular pentagons; the pattern also contains irregular 7-pointed stars between 3- and 2-fold centers.

Ermenek, Ulu Camii, 1302                                       Bey§ehir, E§refoglu Camii, 1296

Fig.17. Patterns with 24-pointed stars.

The predecessor of the latter pattern is the giant rosette on the concave dome of the Karatay madrasah in Konya, built in 1254 (Fig.18). The 24-pointed stars are located here in four concentric rings, the spaces between them increase as they go away from the center, and therefore the interlacing of the ribbons in each ring becomes more complicated, not having any specific symmetry, except for the rotational symmetry of the entire dome as a whole.

Fig.18. The dome of Karatay madrasah in Konya.

Wallpaper group p6

The p6 wallpaper group has the same centers of rotational symmetry as the p6m group, however it have not any mirror symmetry. Structures appear around its symmetry centers can be called “pinwheels” or “vortices”. In the Konya Sultanate, almost all patterns of the p6 group are made with mosaics of narrow strips (Fig.19); this type of mosaic is not represented anywhere else. To compare the patterns, I orient mosaic strips at angles of 0°, ±60° to the vertical, although in situ some of them have such angles to the horizontal. The lattice of symmetry centers is not necessarily aligned along the same directions, often rotated relative to them.

Konya, Tahir ile Zuhre Mescidi, c. 1270                                Akjehir, Ta? Medrese Mescidi, 1250                                Konya, Tahir ile Zuhre Mescidi, c. 1270

Akjehir, Kucuk Ayasofya Mescidi, 1236                                 Malatya, Ulu Camii, 1247                                      Tokat, Gok Medrese, 1277

Fig.19. Patterns of p6 group.

This section is completed by three patterns with square swastikas (Fig.20). The second and the third patterns have exactly the same scheme embodied in different colors. In a simpler version without swastikas, this motif first appeared at the Khar- raqan west tower (1093).

Kaysery, Hunat Hatun Kiilliyesi, 1238                               Sivas, izzeddin Keykavus TOrbesi, 1220                                  Konya, Karatay Medresesi, 1254

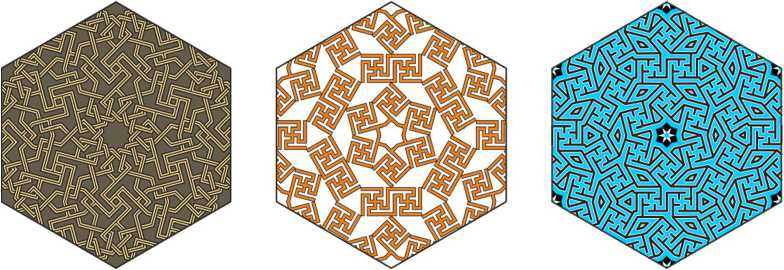
Fig.20. Patterns of p6 group with square swastikas.

Wallpaper group p31m

The p31m group has two families of 3-fold rotational centers; in Fig.21 they are shown as red and green triangles. Three axes of mirror symmetry pass through the “red” centers, forming triangular lattice. Through the “green” centers the axes of mirror symmetry do not pass, and these centers are surrounded by a “vortex” structure, as in the p6 group.

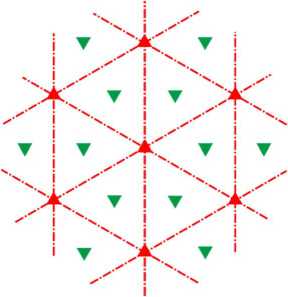
Fig.21. Lattice of p31m group.

There are not many patterns of this group in the Konya Sultanate (Fig.22). The seventh pattern with “snowflakes” appears earlier at the Kharraqan west tower (1089). The eighth pattern with 9-pointed stars visually differs from the others, and to notice its relationship with them, one can combine the star with three adjacent trefoils.

Konya, Sirrah Mescit, c. 1270

Aksaray, Cincikli Mescit,c. 1250

Sivas, Buruciye Camii, 1271

Atyon, Misri Camii (1483)

Konya, $eyh Sadreddin Conevf Camii, 1274

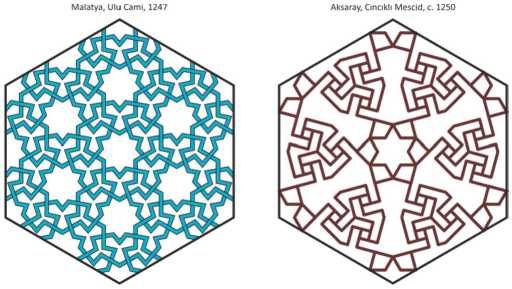
Fig.22. Patterns of p31m group.

Wallpaper group p3m1

The p3m1 wallpaper group has three different families of 3-fold rotational symmetry centers; three axes of mirror symmetry pass through any center (Fig.23).

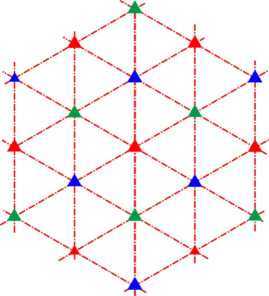
Fig.23. Lattice of p3m1 group.

Among the patterns of the Konya Sultanate I found only four examples of this group (Fig.24). All the patterns, except the first one, belong to this group due to the coloring of their details, which converts p6m group into p3m1.

Konya, Karatay Medresesi, 1254                                    Tokat, Ali Tusi Turbesi, 1234

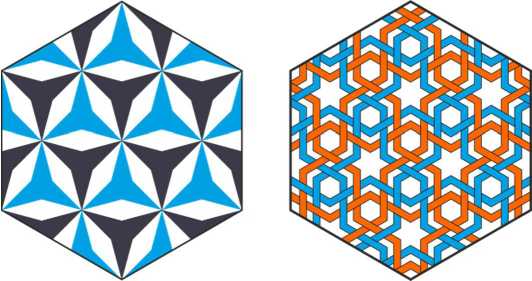
Fig.24. Patterns of p3m1 group.

Wallpaper group p3

The p3 group has three different families of 3-fold symmetry centers without mirror symmetry axes. The only pattern belonging to this group is shown in Fig.25, where the multiple inscription “Ali” is written in Kufic script. Three dark and three light inscriptions converge at one point, differing from each other only in color. The other two 3-fold symmetry centers of this pattern are located at the junctions of three dark or three light stripes.

Akjehir, AlaeddFn Camii, c. 1235

Fig.25. “Sixfold Ali” pattern.

Wallpaper group p4m

From the patterns on a hexagonal lattice we move to the patterns on a square lattice. We begin this part of our review with patterns of the p4m group, which plays in the case of a square lattice the same role as the p6m group in the case of a hexagonal lattice. These patterns have two families of 4-fold rotation centers (red and green squares in Fig.26) and a family of 2-fold rotation centers (blue rhombuses). Two families of mirror symmetry axes are shown here in red and blue dash-dotted lines. Selecting a symmetrical fragment of such a pattern, one can place both the

“red” and “green” centers in the center of this fragment. In addition, the entire pattern can be rotated by 45°, which gives four different visually perceived ornaments based on the same geometric pattern.

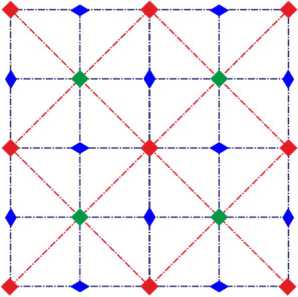
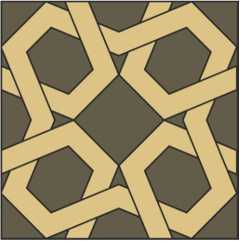
Fig.26. Lattice of p4m group.

The simplest patterns of this group consist of 4-pointed stars and rhombuses, which complement these stars to regular octagons (Fig.27). The fifth pattern here contains also regular 6-pointed stars. The sixth pattern is built on a simple square lattice with diagonal jugs.

Konya, Karatay Medresesi, 1254                                Konya, Karatay Medresesi, 1254                                  Konya, Sirrah Mescit, c. 1270

Fig.27. The simplest patterns of p4m group.

The patterns of the p4m group usually were used to decorate the frame of the portal. The first pattern in Fig.28 is formed by interlacing regular octagonal ribbons and is the same with the last sixth pattern in previous Fig.27. This simple design is quite widespread, and its earliest known example is on the Kharraqan eastern tower (1068). The 7th pattern also is found in many buildings of the pre-Mongol period, starting with the Friday Mosque minaret in Damghan (1029). The 16th and 17th patterns have the same scheme, in which an eight-pointed star (of two different kinds) is surrounded by eight its copies. In the last three patterns, 5- and 6-pointed stars appear.

Aksaray-Kayseri, Sari Han, c. 1235

Bitlis, Memi Dede Mescidi, (1572)

Bitlis, Memi Dede Mescidi, (1572)

Hani, Hatuniye Medresesi, 1212

Corum, Ulu Camii, 1306

Konya, Sirrah Medrese, 1242

Aksaray-Konya, Sultan Hani, 1229

Konya, Alaeddin Camii, c. 1235

Konya, Alaeddin Camii, c. 1235

Afyon, Misri Camii, (1483)

Fig.28. The basis of these patterns is a regular octagon or 8-pointed star.

Tokat-Pazar, Mahperi Sultan Hani, 1239

The next two patterns (Fig.29) contains regular pentagons in their design, so they are related to the p6m patterns with regular pentagons in Fig.7. The first pattern decorates several buildings of the second half of the 12th century, as the Abiwerd peshtak, the palace of Termez rulers, the Shah-i Mashhad madrasah in the Afghan province of Badghis (1176) and the Jam minaret (1194). It is also one of the most popular designs in the Konya Sultanate, being reproduced with different proportions in Alâeddin Mosque (1235), Karatay Madrasah (1251) and Sahib Ata Mosque (1258) in Konya, also in Eşrefoglu Mosque (1296) in Beyşehir.

Fig.29. Two patterns with octagons, squares and regular pentagons.

Three next patterns (Fig.30) have a structure with eight regular pentagons attached to the sides of a large regular octagon. The second pattern, now completely painted over with gold paint, is located in the mihrab of Piri Mehmet Pasha Mosque in Konya, which dates back to 1523 (see Fig.2). However, this pattern firstly appeared in the palace of Termez rulers, which suggests that it was transferred to this mosque from an earlier building.

Fig.30. Three patterns with 8-pointed stars and regular pentagons.

The next three patterns (Fig.31) have 12-pointed stars in 4-fold centers. The first pattern is the simplest of them, the 12-pointed stars here adjust to each other directly by their vertices. Two next patterns contain the “glue” of 5-pointed stars.

Van, Ulu Camii,13 c.                                       Sivas, izzeddin Keykavus Tiirbesi, 1220                             Sivas, izzeddin Keykavus Tiirbesi, 1220

Fig.31. Patterns with 12-pointed stars.

The next two patterns (Fig.32) have 16-pointed stars in 4-fold centers with the

“glue” of 5-pointed stars or more complicated figures.

Fig.32. Patterns with 16-pointed stars.

Balat, Ilyas Bey Camii, 1403

The first pattern at Fig.33 has 12-pointed stars and octagons at 4-fold centers, and 10-pointed stars at 2-fold centers. Also it has 9-pointed stars at symmetry lines and 5-pointed stars as a glue. The next two patterns are built on the same basis, although outwardly they don’t look alike. Both of them have 16- and 8-pointed stars at 4-fold centers, and 12-pointed stars at 2-fold centers. Also they have 10-pointed stars at symmetry lines.

Fig.33. Patterns with additional stars.

Both patterns in Fig.34 have 8-pointed stars or octagons in 4-fold centers. Also they contain 7-, 6-, 5-pointed stars.

Fig.34. Patterns with different stars.

Wallpaper group p4

The p4 group has the same two families of 4-fold symmetry centers and one family of 2-fold symmetry centers as the p4m group, but without mirror symmetry axes. The first three patterns in Fig.35 go back to prototypes known from the design of columns in the palace of Termez rulers (late 12th century). All three families of rotational centers are emphasized here by different figures. The rectangular design of the fifth pattern is based on brickwork, which was used in Khorasan in the 11th– 12th centuries.

Kayseri, Haci Kill? Camii, 1249                                     Beyjehir, Ejrefoglu Camii, 1296                                    Kayseri-Sivas, Sultan Hani, 1232

Akjehir, Altunkalem Mescidi, 1223                            Karaman, Hatuniye Medresesi, 1381                                  Divrigi, Ulu Camii, 1228

Fig.35. Patterns of p4 group.

The last five patterns in Fig.36 embody the same idea as the patterns of the p6 group in Fig.20. Here the pattern of the p4m group with square elements in its structure is taken, and then each square is filled with a swastika-shaped ribbon, rotating in the same direction. The last two patterns are totally identical; this design firstly appears in the more simple form in the Kharraqan east tower (1068).

Kayseri, Hunat Hatun Kulliyesi, 1238                             Sivas, izzeddin Keykavus Turbesi, 1220                                 Konya, Karatay Medresesi, 1254

Fig.36. Patterns of the p4 group with swastikas in squares.

Wallpaper group p4g

The p4g group has one family of 4-fold centers and one family of 2-fold centers, while the axes of mirror symmetry pass only through the 2-fold centers (Fig.37), so 4-fold centers acquire a vortex character.

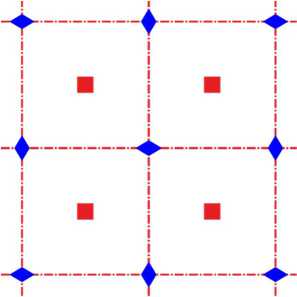
Fig.37. Lattice of the p4g group.

The 4-fold centers of the patterns shown in Fig.38 are marked with swastikas or

octagons.

Konya, Sir^ali Medrese, 1242                                    Amasya, Halifet Gazi Turbesi, c. 1220                                Konya, Karatay Medresesi, 1254

Fig.38. Patterns of the p4g group.

Note that the octagons and the 8-pointed stars of two last patterns in Fig.39 do not mark centers of symmetry, although they lie on the axes of symmetry. (The third pattern belongs to p4g group, if we do not distinguish between blue and orange ribbons).

Kayseri, Haci Kill? Camii, 1249 Isparta-Antalya, Susuz Han, 1245 Amasya, G6k Medrese, c. 1250

Fig.39. Patterns of the p4g group.

Some other wallpaper groups

As noted above, 17 distinct wallpaper groups exist in total, and 8 of them have already been discussed. We will not discuss all the remaining 9 groups here, but consider only those on which other architectural patterns of the Konya Sultanate are based.

pmm cmm pmg

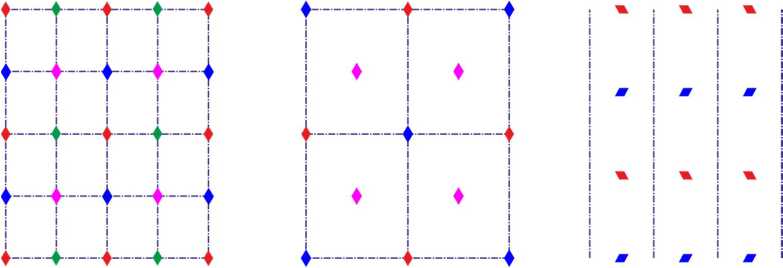
Fig.40. The lattices of the pmm, cmm, pmg groups.

The lattice of the pmm group is formed by two mutually perpendicular families of symmetry axes. Four families of 2-fold centers are located at their intersections. The centers of each of these families form a rectangular lattice.

The lattice of the cmm group also has two mutually perpendicular families of symmetry axes. Two families of 2-fold symmetry centers are located at their intersections. The centers of each of these families form a rhombic lattice. In the centers of elementary rectangular cells there is another one family of 2-fold symmetry centers. The centers of this family form a rectangular lattice.

The lattice of the pmg group has one family of symmetry axes. Two families of 2-fold symmetry centers are located on straight lines perpendicular to the symmetry axes.

Patterns of 5-fold system

Unlike squares and regular hexagons, regular pentagons and decagons cannot tile a plane. Therefore, the patterns based on these figures are built on the rectangular lattice using additional elements. In the 11th–12th centuries, such patterns are few in number, but there are their outstanding examples in the Friday Mosque in Isfahan (1089) and in the palace of Termez rulers (late 12th century).

The simple pattern of this kind occurs when equal pentagons are arranged in rows touching their apexes, with “jugs” between them (Fig.41). This pattern belongs to cmm group.

Afyon, Misri Camii (1483)

Fig.41. The simplest pattern with pentagons and jugs.

We continue this review with border strips containing regular pentagons (Fig.42). These patterns also contain specific hexagons, rhombuses, jugs, bow ties and other typical shapes, all angles of which are multiple of 36°. To understand the richness of such a pattern, we need to draw different axes of symmetry of the pentagons and see how these pentagons fit together. In the last two patterns, the pentagons are replaced by five-pointed stars with angles of 72° at their vertices.

Konya

Sahib Ata Hanikahi, 1258

Konya

Beyjehir

Kayseri

Sahibiye Medresesi, 1267

Karatay Medresesi, 1254

E§refoglu Camii, 1296

Malatya

Ulu Cami, 1247

Afyon

Misri Camii, (1483)

Konya

Sahib Ata Camii, 1258

Konya

Sir?ah Medrese, 1242

Ankara

Arslanhane Camii, 1289

Konya

Tahir ile Zuhre Camii, ca. 1270

Fig.42. Patterns on the base of regular pentagons.

Classic patterns of this kind are based on 10-pointed stars, using pentagons, jugs, bows and kites (Fig.43). In the first pattern the 10-pointed stars are adjacent to each other by their vertices. The earliest known example of this pattern is in the Friday Mosque of Isfahan (1089); this pattern is also found in the palace of Termez rulers (late 12th century). In the second pattern the 10-pointed stars are adjacent to each other by the spaces between the vertices. In the third pattern the 10-pointed stars are adjacent to each other by their vertices again, but not directly, through the rhombuses. All these patterns belong to the cmm group.

Fig.43. Patterns with 10-pointed stars, pentagons and jugs.

Two patterns in Fig.44 shows a more complex design from the same elements. In the second pattern internal 10-pointed star is surrounded by 10 pentagons, 10 bows and jugs, 20 pentagons, 10 jugs and pentagons, and 20 pentagons, forming a big rosette. These patterns belong to the pmm group.

Konya, Beyhekim Mescidi, c. 1270

^ay, Ta? Medrese, 1268

Fig.44. Complex pattern from standard elements.

The next series of patterns (Fig.45) also demonstrates the capabilities of a mosaic set, constructed from the same elements. The first pattern is very widespread; its early examples are the palace of the rulers of Termez (late 12th century), Sitte Melik Mausoleum in Divriği (1196), Mama Hatun Mausoleum in Tercan (c. 1200), Zozan

Madrasah in Khorasan (1212). The second pattern is designed by horizontal expanding of the first one, cutting it along the vertical axis, and inserted 10-pointed stars.

Fig.45. Possibilities of the pattern design.

The first pattern at Fig.46 is made up of stars with angles of 36° at the vertices; this case requires a “glue” of regular 5-pointed stars. In the next three patterns, the joining of 10-pointed stars becomes more sophisticated.

Fig.46. Patterns with 10-pointed stars.

The pattern in Fig.47 reproduces the structure of the first pattern in Fig.43, except that the 10-pointed stars in it have a more sophisticated form. These stars are shown in red on the diagram. The spaces between the stars are filled with double kites shown blue. This pattern belongs to the pmg group.

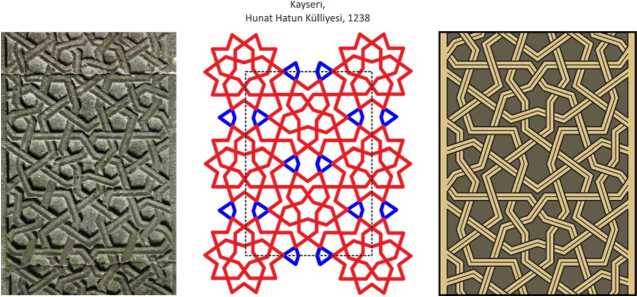
Fig.47. Assembling a pattern with 10-pointed stars and kites.

The next pattern (Fig.48) consists of the same stars shown red, bows shown green and kites shown blue.

Kayseri, Hunat Hatun Kulliyesi, 1238

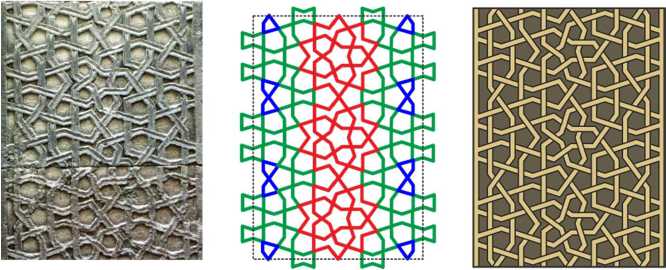
Fig.48. Assembling a pattern with 10-pointed stars, bows and kites.

The next two patterns (Fig.49) consist of 10-pointed stars, bow ties and jugs again. The 10-pointed stars are arranged inside differently than in the two previous patterns, so that they have not a 5-pointed star, but a pentagon in their center. The difference between the two patterns in Fig.49 is only which way the internal pentagons in the two side columns are turned, with the vertices inward or outward.

Fig.49. Assembling two patterns with 10-pointed stars, bows and kites.

The following pattern (Fig.50) is composed only of kites shown blue and jugs shown purple. The kites are combined by ten into 10-pointed stars of the same shape as in several previous examples. Of course, these simple stars can be replaced by the complex ones, and I did this especially in the left half of the diagram.

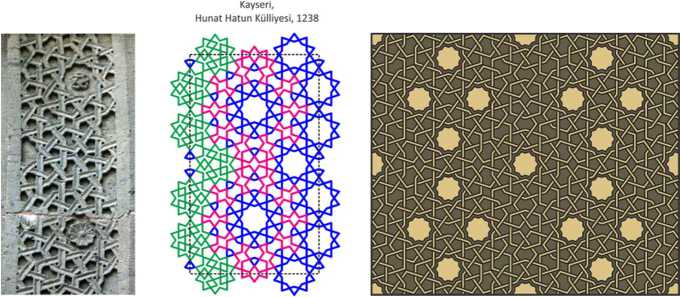
Fig.50. Assembling a pattern with kites and jugs.

Another modular assembly pattern, including 10-pointed stars (red), bows united in five (green), jugs (purple), kites (blue) and large 10-fold rosettes (brown), is shown in Fig.51; it is the most complicated pattern of this type in the Konya Sultanate.

Konya, Karatay Medresesi, 1254

Fig.51. Assembling a pattern from enlarged elements.

Although it is impossible to tile a plane on the base of 10-fold or 5-fold symmetry, it is possible to construct a rosette with this symmetry around a given center. Two examples of this kind with central 10-pointed star are shown in Fig.52.

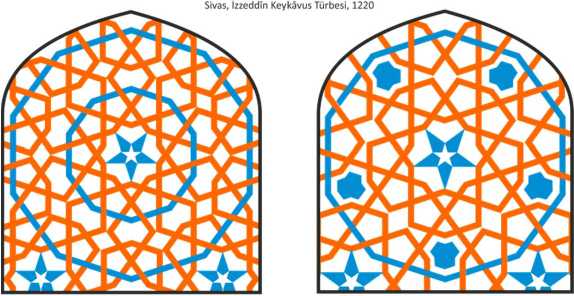
Fig.52. Rosettes of 10-fold or 5-fold symmetry.

Some other rosettes of 5-fold symmetry are shown in Fig.53. All of them contain a closed chain of 10 regular pentagons, connected to each other by their vertices, and differ from each other only by the inner structure of the central 10-pointed star.

Kayseri, Hunat Hatun Kiilliyesi, 1238

Fig.53. Rosettes of 5-fold symmetry.

Kayseri, Alaca Kiimbet, 1280

Patterns of 5-fold system with “pinwheels”

The next two patterns also are based on regular pentagons, but I decided to consider them separately from others. The reason of such a decision is that these patterns are arranged on the principle of pinwheels.

The basic structure of the first pattern consists of large pentagons and kites (Fig.54). Each large pentagon is cut into a small central pentagon and five surrounding strips, forming a pinwheel. Each kite is connected with two strips of two adjacent pinwheels, forming a typical “duck” shape. This pattern belongs to the pmg group.

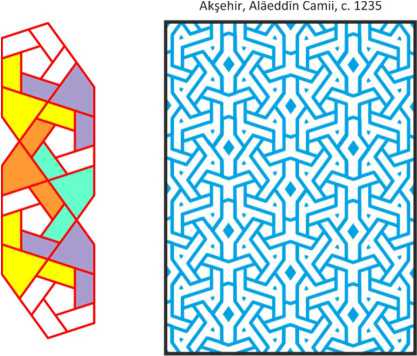
Fig.54. This pattern with pinwheels is based on pentagons.

The second pattern is reconstructed from two fragments kept in the ceramics museum in the Karatay madrasah in Konya (Fig.55). All pentagons here are centers of pinwheel structures again. I have shown here not only the final construction (on the right), but also two simpler patterns with the same basic tessellation structure (blue lines), so that the path of invention that led to this result can be seen.

Konya, Karatay Medresesi Museum

Fig.55. This complicated pattern also is based on pentagons.

Pinwheel patterns based on pentagons are called pili in Farsi. This decorative motif in 5-fold structures is quite rare. The two patterns shown above are the earliest to survive to this day. However, I assume that at this time there were more patterns of this kind, such as later patterns from the Friday Mosque in Yazd (1375) and Shah Mosque in Isfahan (1611).

Patterns of 7-fold system

The simplest pattern of this system based on adjacent regular heptagons is shown in Fig.56. Heptagons are arranged in horizontal rows with tipping at every step, and these rows are adjacent to each other. The centers of six heptagons form a barrelshaped hexagon with angles of 2/7 and 3/7 of a full 360° angle.

Egirdir, Dundar Bey Medresesi, 1301

Fig.56. A simple pattern with regular heptagons.

Another two patterns with 7-pointed stars, which are based on the same structure, are shown in Fig.57. In the barrel gap between 7-pointed stars, the first pattern con- tains two 5-pointed stars, and the second pattern contains two small pentagons.

Fig.57. Patterns with 7-pointed stars.

Other patterns on rectangular lattice

This final section begins with frieze stripes based on different elements with angles multiples of 45° (Fig.58).

Fig.58. Framing stripes.

The pattern in Fig.59 belongs to the pmm group. It contains 14-, 10-, 7-pointed stars

and octagons, with a “glue” of 5-pointed stars.

Fig.59. The pattern of the pmm group.

Three patterns in Fig.60 belong to the cmm group. The first pattern is based on a square lattice. If its tiles were not distinguished by color, this pattern would belong to the p4g group. The second and the third patterns are based on a rectangular lattice. The third pattern appears for the first time in Momine Khatun mausoleum in Nakhichevan (1186).

Fig.60. Three patterns of the cmm group.

Two patterns in Fig.61 belong to the pmg group. They consist of arrows pointing up and down; in the second pattern the design becomes more complex due to the presence of a deformed swastika.

Egirdir, Diindar Bey Medresesi, 1301                        Konya, Sahib Ata Camii, 1258

Fig.61. Two patterns of pmg group.

Patterns on the surface of cuboctahedron

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. It can be obtained either by cutting off the vertices of a cube or by cutting off the vertices of an octahedron, which is why it has this name.

The cuboctahedron is one of the 13 semi-regular, or Archimedean solids. These are solids whose faces are regular polygons of at least two types, and all vertices have one vertex figure. Sabit ibn Qurra wrote a treatise on the construction of a cuboctahedron inscribed in a given sphere. Abu al-Wafa al-Budzhani considered methods to tessellate a sphere into equal parts, leading to the construction of regular and some semi-regular polyhedra, and the cuboctahedron in particular, in his work On the Geometrical Constructions Necessary for the Artisan.

Fig. 62. Ornamental patterns on the surface of cuboctahedron.

Inscriptions

A special kind of patterns is formed by inscriptions in square Kufic script with regularly repeating elements. Here we consider nine inscriptions on the pendentives of Karatay Madrasah in Konya (1254). Seven of them belong to the p4 wallpaper group, and the elements of the inscription can be parallel to the lines of the square lattice or inclined to them. One inscription is executed on the basis of the p2 group, with an oblique lattice cell. Another one inscription is executed on the basis of the p1 group, so it contains only translational symmetries, with a rectangular lattice cell.

Muhammed (p4)                                            Ali(p4)                                            Muhammed (p4)

Fig. 63. Inscriptions in Konya Karatay Madrasah.

Why are there so many patterns?

This review contains drawings of about 280 patterns, and some more patterns may have be missed by me, and some more have not survived to this day. There are a great variety of patterns, and a significant part of them are found only once in one place. So we should ask ourselves what this diversity of patterns is connected with, and try to give a plausible answer.

Of course, the master of ornaments wanted to amaze everyone with the unusualness and novelty of what he was creating, with something that no one had ever seen before. His geometrical pattern was a challenge to other masters, to his colleagues in the architectural profession. But this diversity also has a philosophical aspect, and it lies in the fact that the master sought to show the diversity of the world of phenomena, the world of veils, behind which lies the unity of the world of ideas, the world of numbers and figures, the world of thought. And in this sense, he was both a philosopher and an artist. So today, the ornament lives on in places where it is not treated as decor “in the national spirit” (it has nothing to do with the national spirit, because there are no carpets with geometric ornaments, etc.), but where the spirit of art, the spirit of invention and research are invested in it.