Геометрическая интерпретация двухкритериальной дискретной задачи

Визуальное описание геометрии оптимизационных задач ускоряет процесс их решения по сравнению с методами оптимизации и делает его более простым и наглядным. В статье разрабатывается геометрическая интерпретация двухкритериальной дискретной задачи, базирующаяся на результатах работы [1], что является

актуальным. Поиск решения этой задачи по рисунку является более быстрым, простым и наглядным по сравнению с известными вычислительными методами решения.

Сформулируем массовую двухкритериальную дискретную задачу (1):

n

Z1 = ^li • Xi ^

max

i=1 n

z2 = ^ ri • xi ^ max

i=1

n

^ a • xi < D

i=1

х,Е{0,1),

i = 1,n

Далее построим функционал ф:

n                 n

ф(21, z2) = 0, 5 • ^ li • Xi + 0, 5 • ^ ц • Xi i=1                i=1

Преобразуем его следующим образом:

n

ф(Z1, z2) = ^ 0, 5 • (li + ri) • Xi

i=1

Введем обозначение f_i = 0, 5 • (l_i + r_i), и получим итоговое выражение для функционала ф = z n= ₁f_i • x_i. Таким образом, двухкритериальная задача (1) была сведена к однокритериальной задаче (2):

п

ф = ^ f, • х, ^ max i=1

n

^ a • х, < D

i=1

х, G (0,1],

i = 1, n

Введем дополнительные переменные (3):

n u 1 = ^ f i • X , i=1 n u 2 = ^ a • x , i=1

Далее сопоставим каждому вектору-решению множества X = {X 1 ,X 2 , ...,X 2 n ] точку двумерного пространства (u₁, u₂). Таким образом, множеству X ставится в

соответствие

множество

и =

{и1,и2, _,и2п], где U = (upuJ2). Изобразим (рис. 1) точки множества U на плоскости u10u2, а также ограничение задачи (2) в виде прямой линии, проходящей через точку (0, D) параллельно оси 0u1.

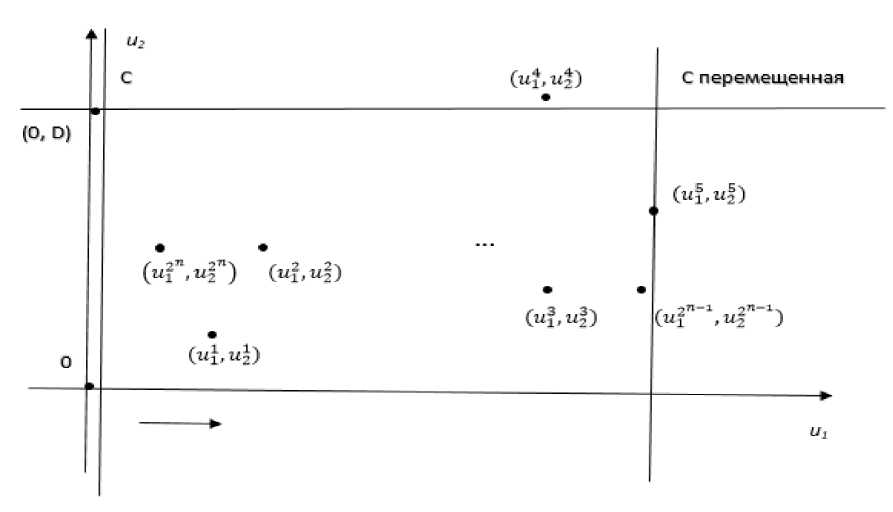
Рис. 1. Геометрическая интерпретация массовой задачи

Изобразим критерий ф этой задачи в виде прямой линии С, проходящей параллельно оси 0u2. Графически будем перемещать прямую С в направлении увеличения u1 параллельно оси 0u2. Крайняя точка, лежащая на перемещенной прямой С, удовлетворяющая ограничению является оптимальным решением задачи (2) - xopt. На рис. 1 - это точка (u2,u2). Следова-

тельно, найдено оптимальное решение задачи (2) - вектор х5 G X. Этот вектор также является оптимальным решением задачи (1).

Рассмотрим и решим двумя способами, с помощью программы и по геометрической интерпретации, индивидуальную двухкритериальную задачу (4):

z 1 = 2, 5x1 + 6,2 5x2 + 8x3 ^ max

z2 = 18,4x1 + 3,2x2 — 16,2x3 ^ max                   (4)

3,5x1 + 8,2x2 — 6,25x3 < 8

x, e {0,1}, i = 1,3

Построим функционал ф для задачи (4):

ф = 0,5 • (2, 5x1 + 6,25x2 + 8x3) +

+0, 5 • (18,4x1 + 3,2x2 — 16,2x3) = 10,45x1 + 4,725x2 — 4,1x3

Запрограммируем в решателе lp_solve однокритериальную задачу (5), полученную сверткой критериев задачи (4):

u1 = 10,45x1 + 4,725x2 — 4,1x3 ^ max

u2 = 3, 5x1 + 8,2x2 — 6,25x3 <8                            (5)

x, e {0,1}, i = 1,3

На рис. 2 представлена программа, вычисляющая оптимальное решение задачи (5). На рис. 3 приведены результаты ее работы.

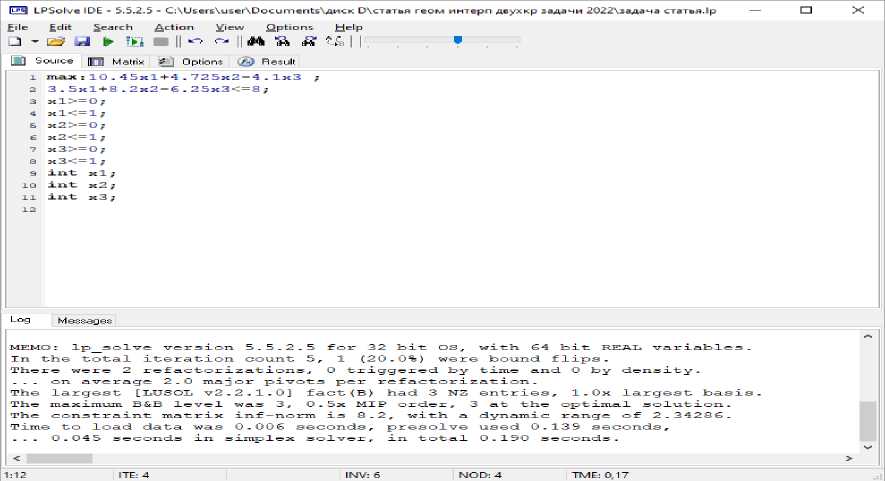
Рис. 2. Программа решающая индивидуальную задачу

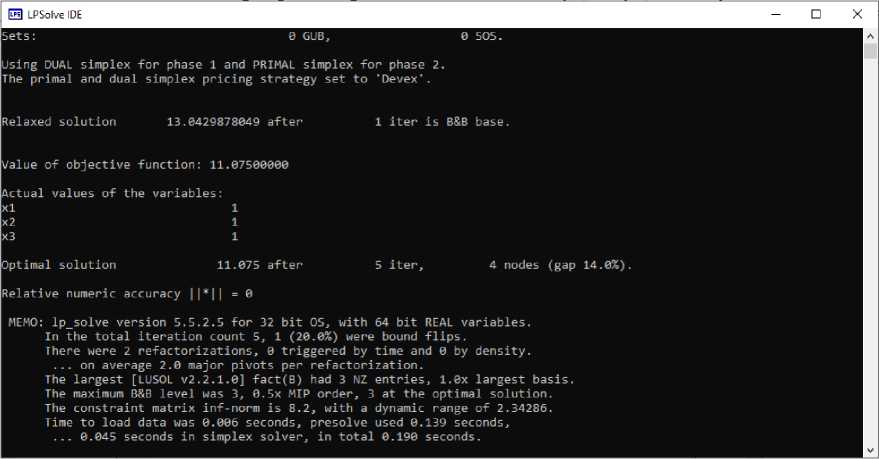
Рис. 3. Результаты работы программы

Решим задачу (5) с помощью геометрической интерпретации. Для этого строим множество X мощности 18| -

X = {(0,0,1), (0,1,1), (1,1,1), (1,0, 0), (1,1, 0), (1,0,1), (0,1, 0), (О, 0,0)}.

Строим множество U =.

{(-4,1; -6,25), (0,625; 1,95), (11,075; 5,45), (10,45; 3,5), (15,175; 11,7), (6, 35; -2, 75), (4, 725; 8,2), (0; 0)}}

На рис. 4 изобразим точки множества U на плоскости u₁0u₂. Ограничение задачи (5) изображается на рисунке прямой линией, проходящей через точку (0,8) параллельно оси 0U 1 . Критерий этой задачи - прямая линия С.

Перемещая прямую С в направлении стрелки, определяем крайнюю точку, удовлетворяющую ограничению. Эта точка (11,075; 5,45), которая соответствует вектору Х 3 Е X.

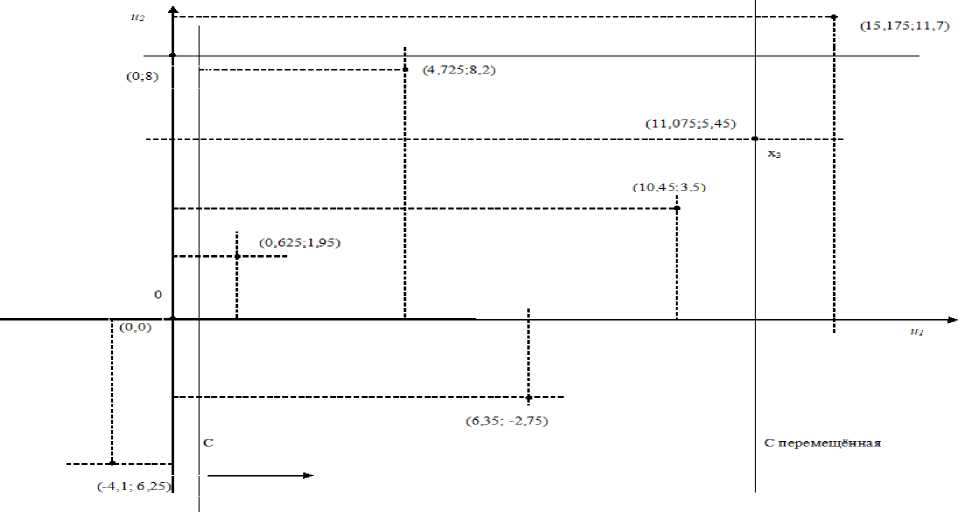
Рис. 4. Геометрическая интерпретация индивидуальной задачи

Таким образом, результат решения задачи (5) по геометрической интерпретации совпадает с программным, этот факт является подтверждением истинности теоретических положений для массовой задачи (1). Следовательно, решена задача (5) – м1 = 11,075; xopt = х3 = (1,1,1). Также

Х 3 является оптимальным решением задачи (4).

В статье разработан новый универсальный способ построения геометрической интерпретации массовой двухкритериальной дискретной задачи, который даёт возможность просто и быстро решать любую задачу класса (1).