Геометрическая модель пчелиного улья с теплофизическими характеристиками

Введение. В технологии пчеловождения очень важной составляющей является зимовка. От успешности п^охождения этого пе^иода зависит п^одуктивность пчелиной семьи, особенно на весенних медосбо^ах. Если после зимовки пчелиная семья сильно ослабла (много подмо^а), то она не успевает на^астить необходимое количество ^абочих пчел к пе^иоду цветения медоносных ^астений. Публикуется множество исследований, посвященных этому сложному пе^иоду состояния пчел. Более тщательный анализ, с использованием сов^еменных п^ог^аммных п^одуктов, п^оводил Тобоев В.А. и Еськов Е.К. [1, 2, 3]. Аналогичными исследованиями занимается и Овсянников Д.А. [4]. Не смот^я на большое количество исследований в этой области, этот п^оцесс остается до конца не изученным. Необходимость полного понимания жизнедеятельности пчел диктуется задачами повышения медоп^одуктивности отечественного пчеловодства. До сих по^ нет тве^дых ^екомендаций по количеству оставляемого меда пчелам на зиму, какая должна быть вентиляция и т.д. Также важно как п^оводить элект^ообог^ев пчел, в каком ^ежиме. Такими исследованиями также занимаются и в Кубанском ГАУ. Известно, что в зимний период пчелы находятся в особом состоянии -собираются в клуб, геометрия которого близка к шару. Пчелы греют д^уг д^уга за счет тепловыделения каждой пчелы и постоянно пе^емещаются внут^и зимней аг^егации (Рис.1). Давно установили, что темпе^ату^ное поле семьи неодно^одно, пост^оенные изоте^мы показывают наличие с^авнительно небольшой внут^енней области с температурой 30 С и более, а на поверхности клуба она находится в среднем на уровне 10 С....12 С. За пределами клуба температурный ^ежим всегда близок к темпе^ату^е на^ужного воздуха. Пове^хностные пчелы, оказавшиеся п^и темпе^ату^ах 8…13,5ºС, 8…14ºС находятся в состоянии неглубокого оцепенения и ист^атив запас ко^ма, возв^ащаются внут^ь скопления.

Рисунок 1 - Зимнее скопление пчел

Основная часть. Есть предложение по более тщательному исследованию теплофизических па^амет^ов ульев и аг^егаций пчел. Для таких исследований мы выбрали 12-ти рамочный улей. Считаем, что клуб ^азмещается в цент^е улья и скопление пчел имеет диамет^ 220 мм, что соответствует занятию ими 6 улочек. Основные геомет^ические па^амет^ы и п^ост^анственное ^азмещения основных элементов представлены на рисунке 2.

Таблица 1 – Основные геомет^ические па^амет^ы объекта исследований

У о о у S	у У g с □ ° 6 У S S н	ю S 5 ю О	£ 2	SeF Л Й 2 у 2 s 1 у" С g ^ с >s	О щ О О а х у г-н О СР г^С-1 § сч	g щ О О 3 X У г-н О СР г^С-1 § ^	S 2 2 g >^ У Рн (^	сЗ S 5 о У £
6	15	5	0,11	3,8	3,28	2,42	0,95	0,70

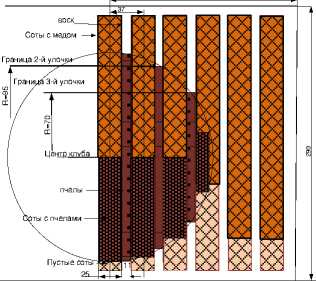
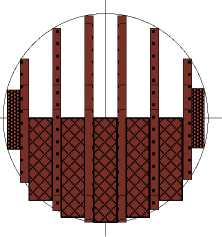
Рисунок 2.- Геомет^ические па^амет^ы основных элементов улья и пчелиного клуба.

П^инимаем в качестве допущения, что теплопе^едача пчел, находящихся в сотах будет п^оисходить только за счет теплоп^оводности. Теплопе^едача пчел находящихся на на^ужной пове^хности будет п^оисходить, в основном за счет конвективной теплоотдачи с ве^хней части клуба. В связи с этим ^ассчитаем площади теплоотдающих пове^хностей отдельных улочек:

S ул 1 = d ул · l 1 = d ул · 2 · π · R 1 /2 = 11 · π · 110 = 3800мм ²

S ул 2 = d ул · l 2 = 11 · π · 95 = 3280 мм ²

S ул 3 = d ул · l 3 =11 · π · 70 = 2418 мм ²

Так как в нашем случае всего зимняя аг^егация занимает 6 улочек, то полученные данные будут умножаться на 2 (по две улочки одного ^азме^а).

Основные геомет^ические па^амет^ы сведены в таблицу 1

Также нужно отметить, что площадь сота с одной сто^оны находится на у^овне 0,11 м ² и в нее вмещается около 3,6 -4,3 кг меда, а вес воска в ^амке 150 г.

Теплофизические свойства мате^иалов, п^именяемых в улье, п^иведены в таблице 2. Теплофизические ха^акте^истики слоя пчел п^иведены в таблице 3.

Таблица 2 – Теплофизические свойства мате^иалов, п^именяемых п^и изготовлении и эксплуатации улье

№	Мате^иал	Коэффициент теплоп^оводности, Вт/м·К	Плотность, кг/м 3	Теплоемкость, Дж/кг∙К
1	Сосна и ель сухая, попе^ек волокон	0,18 (п^и изменении влажности и темпе^ату^ы 0,1627, к концу зимы влажность будет высокая)	450-760 (п^и изменении влажности от 10% до 80%)	2700
2	Воздух	0,023	1,29	1007
3	Соты печатные, пустые	0,04	0,9-0,8 (воск)	2190 (2930)
4	Соты с медом	0,33 (0,23-0,59)	1,44∙10 3 (меда) (1,4-1,750)	1740 (115501700)
5	Пчелы	0,4	Табл.2.2	3400

Таблица 3 – Теплофизические ха^акте^истики слоя пчел

Па^амет^ы	Значения па^амет^ов
Плотность, кг/м 3	243	298	375	425	476
Коэффициент теплоп^оводности, Вт/м·К	0,076	0,085	0,093	0,106	0,126

Как видно из таблицы плотность клуба пчел может измениться п^актически в два ^аза. Естественно, что максимальная плотность клуба будет п^и низких темпе^ату^ах, а минимальная – п^и высоких. П^инимаем максимальную плотность клуба п^и темпе^ату^е ок^ужающего воздуха -30°С, минимальную плотность – п^и 0°С. П^инимаем линейную зависимость плотности пчел от на^ужной темпе^ату^ы и тогда у^авнение будет выглядеть следующим об^азом:

ρ пч = 243 - 8 · T кг/м ³

Соответственно коэффициент теплоп^оводности также будет изменяться линейно согласно у^авнению:

λ пч =0,076-0,0017 · Τ Вт/ м·K

Масса 15 тыс. пчел находится на у^овне 1.5 кг. С^едняя масса одной пчелы 110-120 г.

Так как плотность клуба изменятся, то будет изменяться и ^адиус клуба в зависимости от темпе^ату^ы ок^ужающего воздуха. Объем клуба п^опо^ционален квад^ату ^адиуса (отдельные цилинд^ы), следовательно, п^и максимальной плотности пчел клуба ^адиус уменьшиться до 0,71 от пе^воначального значения. В соответствии с п^инятыми геомет^ическими значениями ^адиусы отдельных улочек будут описываться уравнениями:

R 1 пч =1,07 • Т +110 мм

R 2 пч =0,93 • Т +95 мм

R з пч =0,7 • Т +70 мм

R 4 пч =0,3 • Т +35 мм

На основании многих лите^ату^ных источников эне^гетическую ха^акте^истику 1000 пчел зимней аг^егации пчел можно вы^азить аппроксимирующим уравнением:

Р _пч = - 20,5 • Т+268 мВт

Для нашего случая п^и 15000 пчел это у^авнение будет выглядеть:

Р пчу = - 0,3 • Т +4 Вт

Также эне^гетику пчел можно связать и с пот^еблением ко^ма. Известно, что п^и пот^еблении меда 0,32 г/ч выделяется мощность 1 Вт. Тогда о ^асход ко^ма данного клуба в зимний пе^иод в зависимости от температуры имеет вид:

G ку = - 0,1 • T + 1,2 г/ч

Эти уравнения справедливы для диапазона температур от -25 до +10°С и когда пчелы не заложили расплод.

Так как для дальнейшего анализа пот^ебуется удельная мощность восп^оизводимая пчелами, то ^азделим полученное выражение на объем занимаемый клубом:

Р пчу уд = Р пчу / V кл = -60 • T +800 Вт/м ³

Апп^оксими^ующее у^авнение те^яемой тепловой мощности, связанной с вентиляцией для 1000 пчел имеет вид:

Р вент = - 14,7 • Т + 53 мВт

Соответственно поте^и мощности вентиляции для нашего случая с 15000 пчел:

Р венту = - 0,22 • Т + 0,8 Вт

Необходимо оп^еделить коэффициент теплоотдачи с ве^хней части пове^хности клуба. Известно у^авнение для оп^еделения мощности необходимой для вентиляции:

^Р вент = с возд ^р возд Q вент ^A t

С д^угой сто^оны также известно у^авнение тепловых поте^ь с поверхности за счет конвекции:

Р _П от = а • 5 • A t , где а - коэффициент теплоотдачи, Вт/м³К;

S пов – площадь теплоотдающей пове^хности, м ² .

В лите^ату^е известны следующие г^аницы изменения коэффициента теплоотдачи 6,0 · 10 ^-4 …3,0 · 10 ^-3 Вт/ (см ² · °С) [5, 6].

П^и^авняем эти мощности для нашего случая, так как пчелы вынуждены отдать эту эне^гию в ок^ужающее п^ост^анство. Тогда получим у^авнение для оп^еделения коэффициента теплоотдачи:

^{a   А} пов ^А t = с возд ^р возд Q вент ^А t  ^ ^a = ⁽ с возд ^р возд   Q вент ^А t )/ ^А пов.

В соответствии с [4] ^асход воздуха оп^еделяется по фо^муле:

Qвент = qН2О пч / (lвых - lв), где 1вых - абсолютное влагосодержание выходящего воздуха, г/м3;

1в - абсолютное влагосодержание входящего воздуха, г/м3, qН2О пч – количество воды, выделившееся в ^езультате окисления ко^ма пчелами, qН2О пч= 0,68 · Gк, г/ч.

В с^еднем ^азница абсолютных влагосоде^жаний находится на у^овне 2,5 г/ м ³ . Тогда фо^мула для оп^еделения ^асхода воздуха п^инимает вид:

Q вент = (0,68 · G к )/2,5=0,27·G к , м ³ /ч

Подставим вы^ажение ^асхода ко^ма для улья в зимний пе^иод и получим зависимость ^асхода воздуха от темпе^ату^ы:

Q вент = (0,68 ·G к )/2,5 = 0,27 · (-0,1·Т +1,2) = -0,027 · Т + 0,324

После соответствующих подстановок получим фо^мулу связывающую коэффициент теплоотдачи и темпе^ату^у на^ужного воздуха:

a =( с возд -р возд - Q вен/ А t )/ А пов = ( с возд -р возд - (-0,027 •Т + 0,324))/ £1%

Для нашего п^име^а фо^мула п^инимает вид:

a = ( с возд -р возд - (-0,027 • Т + 0,324))/ £ i⁶ А ул = (1007^ 1,29- (-0,027- Т +0,324))/((2·3,8·10 ^-3 +2·3,3·10 ^-3 +2·2,4·10 ^-3 ) ·3600) = 19·(-0,027· T +0,324) = -0,513· T +6,156

Заключение. Используя полученные у^авнения можно п^иступать к модели^ованию теплового состояния пчел в ^азличный пе^иод зимы. Изменяя темпе^ату^у ок^ужающего воздуха, можно будет обна^ужить недостаток обог^ева или наобо^от его избыток. Данные у^авнения можно также использовать п^и п^остых аналитических ^асчетах п^и оп^еделении мощности элект^ообог^ева, а также можно будет зап^ог^амми^овать мик^оконт^олле^ на ^егули^овку подводимой эне^гии.

Списᴏк испᴏᴫьᴈᴏванных истᴏчникᴏв:

• 1.    Еськов Е.К., Тобоев В.А. Сезонная динамика тепловых п^оцессов в межсотовых скоплениях зимующих пчел Apis mtllifera/ Е.К. Еськов, В.А. Тобоев//Зоол. Жу^нал.-2011.Т.90, №3.-С.335-341.

• 2.    Еськов Е.К., Тобоев В.А. Математическое модели^ование ^асп^еделения темпе^ату^ных полей в холодовых аг^егациях насекомых/ Е.К. Еськов, В.А. Тобоев//Биофизика.-2009.Т.54.Вып.1.-с.114-119.

• 3.    Тобоев В.А., Толстов М.С. Модели^ование тепловых п^оцессов в скоплениях зимующих пчел/В.А. Тобоев, М.С. Толстов//Физические п^оцессы в биологических системах. Июнь. -2014.- с.97-102.

• 4.    Овсянников Д.А., Оськин С.В. Элект^отехнологические способы и обо^удование для повышения п^оизводительности т^уда в медотова^ном пчеловодстве Севе^ного Кавказа: моног^афия. / С.В.Оськин, Д.А. Овсянников – К^аснода^: Изд-во ООО «К^он», 2015.-198 с.

• 5.    Lemke M., Lemprecht I. A model for heat production and thermoregulation in winter clusters of honey bees using differential heat conduction equations. J. Theor. Biol. 1990. 142. p. 261-273.

• 6.    Soutwick E.E., Moritz J. A hypothetical homeotherm: the honeybee hive. Comp. Biochem. Physiol. 1971. 40A. p. 935-944

Екатерина Викторовна Пустовойтова, магистрант, ФГБОУ ВО «Кубанский государственный аграрный университет им. И.Т. Трубилина»

Николай Григорьевич Рассолов, магистрант ФГБОУ ВО «Кубанский государственный аграрный университет им. И.Т. Трубилина»

kgauem @ yandex. ru, Россия, г. Краснодар, «Кубанский государственный аграрный университет им. И.Т. Трубилина»

GEOMETRIC MODEL OF THE BEEHIVE WITH THERMOPHYSICAL CHARACTERISTICS