Геометрические характеристики нерегулярных сеток и их поведение при квазиизометриях

1.    Оценка вторых производных

Пусть D ⊂ R ² — область, в которой задана последовательность { P _m } конечных наборов точек. Мы будем рассматривать такие наборы точек P _m , для которых выполнено условие

V x Е D и V s > 0 3 m _o Е N : V m > m ₀ 3 a Е P m такая, что | a — x | <  e .     (1)

Это условие означает, что P m является конечной ε-сетью при всех достаточно больших m.

Рассмотрим некоторую функцию f(x),x Е D класса C(D), дважды дифференцируемую в некоторой точке po = (xo, yo) Е D. Выберем из Pm некоторый набор из пяти точек pi i = 1, вида

..

., 5 и пусть d обозначает максимум длин | p i — p _o | . Рассмотрим функцию

g(x, y) = f o + p(x — x o ) + q(y — y o ) +

+ 2 ( a(x - x o ) ² + 2в(x - X o )(y - y o ) + Y(y - У о ) 2 ) •

Ясно, что g(x _o ,y _o ) = f o = f(x _o ,y _o ). Пусть имеется возможность подобрать коэффициенты так, что f (p i ) = g(p i ),i = 0,5. Выясним, при каких геометрических условиях на расположение точек p _i возможна аппроксимация первых и вторых производных функции f (x,y) соответствующими коэффициентами функции g(x,y). Кроме этого, в работе мы ставим задачу исследования этих условий при квазиизометрических преобразованиях области D. Отметим, что в работе [1] аналогичная задача решалась для аппроксимации первых производных. В книге [2] можно найти решения аналогичных задач в одномерном случае.

Введем обозначения для нормы матрицы A

| Ax | ^k A k = sup . x 6 =0 | x |

Через d^ f (^ 1 , ^ 2 ,..., ^ _k ) мы обозначаем k-й дифференциал функции f (x,y) в точке p ₀ как k-линейную функцию переменных ξ i ∈ R ² . Введем величину

.           ^{|f (}P i ) ^{— f (}P o ) ^— d p o ^{f (}P i ^— P o ) ^— 1 dp₀ ^{f (}P i ^— P o ,P i ^— P o ) |

.

о = max ---------------------:---------------------------- i=1,...,5                                       |pi - p0|2

Ключевым результатом данного параграфа является следующая теорема.

Теорема 1. Пусть S — максимальная площадь треугольников с вершинами в точках p ₀ , p _i , p j . Тогда выполняются оценки:

p

-

df (x o ,y o ) ∂x

≤

α -

d 2 f (x o ,y o ) ∂x ²

β

≤

55d ³ S ³

2A ’

155d6S

| A |

q -

,γ

-

-

d ² f (x o ,y o ) ∂x∂y

df (x o ,y o ) ∂y

≤

55d 3 S 3

≤

d ² f (x o ,y o )

∂y ²

155d6S

1AT ’

≤

2 | A | ’

155d6S

1AT’

где

I 4     ⁵

A = 4 52 jliH)^{i + j +}1 A j A ki A km A im ,

A rq = (a r c q — a q c r ), a r = x _r

-

X o C r = У г

-

y 0 .

Доказательство. Поскольку функция f (x, у) дважды дифференцируема в точке p0, то f (Pk ) = f (Po) + dpo f (Pk

-

P o ) + 2 d p o ^{f (}P k

-

P o ,P k - P o ) + R(P k ),

где R(P k ) <  S \ P k — P 0 | ² и k = 1, 5. Ясно, что

R(P k ) <  5d².

Таким образом, из условий

g(P k ) — f (P k ) = 0, где k = 1, 5

получаем систему уравнений

g(P k ) — f (P k ) = (X k — X o )(P — ^df (Xx¹*) ) + (y k — y o )(q — ^df(| ^ol ^{y o )}) +

+ 1/2((x _e — x o ) ² (a — ^{д 2} f^X21^ ⁰ )) + 2(x ₆ — x o )(y ₆ — y o )(e — ^{d 2} f^(x^^ ^{o )}) + ∂x ²                              ∂x∂y

+ (y k — y o ) 2 (Y — ^d 2 f ⁽ X°’y ^o ) )) — R(P k ) = 0.

∂y ²

Обозначим z1

= P —

df (x o ,y o ) ∂x

Z 2 = q —

df (xo,y o ) ∂y

Z 3 = a —

d ² f (xo,y o )

∂x ^{2     ,}

о ^{d 2 f} (x o ,y o )

z 4 = ^в-----^, z 5 = Y

∂x∂y

-

d ² f (x o ,y o ) ∂y ²

.

Следовательно, akzi + CkZ2 + 1/2ak2z3 + akCkZ4 + 1/2ck2z5 = R(pk), где k = 1, 5.

Запишем данную систему в матричном виде A * z = R, где

A =

/ a i a 2 . .	c 1 c 2 . .	1/2a i2 1/2a 22 . .	a 1 c 1 a 2 c 2 . .	1/2c i2 \ 1 / 2 C 22 . .	, z =	/ z i \ z 2 . .	, R =	/ R(p i )\ R(P 2 ) . .
. a 5	. c 5	. 1/2a 52	. a 5 c 5	. 1 / 2 C 52		. z 5		. R ( p 5 )

.

= R(p _k ). Данную систему будем решать методом Крамера. Для

Пусть для краткости R k

определителя матрицы уравнения получим
	a 1	c 1	1 / 2 a i2	a 1 c 1	1 / 2 C i2
A=	a 2 . .	c 2 . .	1 / 2 a 22 . .	a 2 c 2 . .	1/2C 22 . .
	. a 5	. c 5	. 1 / 2 a 52	. a 5 c 5	. 1 / 2 C 52

Здесь i = j = k = l = m, причем k < l < m.

1/4 X X ( - 1) ^{i + j +1} A ij A ki A km A im .

i =1 j>i

И

далее,

A i

A 2

R 1 R 2 .	c 1 c 2 .	1 / 2 a i2 1 / 2 a 22 .	a 1 c 1 a 2 c 2 .	1 / 2 C i 1 / 2 C 2 .
. . R 5	. . c 5	. . 1 / 2 a 52	. . a 5 c 5	. . 1 / 2 C 5
a 1	R 1	1 / 2 a i2	a 1 c 1	1 / 2 C i
a 2 .	R 2 .	1 / 2 a 22 .	a 2 c 2 .	1 / 2 C 2 .
. . a 5	. . R 5	. . 1 / 2 a 52	. . a 5 c 5	. . 1 / 2 C 5

A 3 ⁼

1/4 52 52( — 1) i ^{+ j + i} $ ij A ki A km A im , i =1 j>i

1/4^^(-1^t+j + 1   AklAkmAim, i=1 j>i

a 1	c 1	R 1	a 1 c 1
a 2 .	c 2 .	R 2 .	a 2 c 2 .
. . a 5	. . c 5	. . R 5	. . a 5 c 5

1 / 2 C 1²

1 / 2 C 2²

.

.

.

1 / 2 C 5²

-

1/2££          Ck CiCm(Aki i=1 j>i

-

^A km + ^A im )

A ₅

a ₁ a 2

.

.

.

a ₅

c 1 c 2

.

.

.

c ₅

1 / 2 a 1²

1 / 2 a 2²

.

.

.

1 / 2 a 5²

a ₁ c ₁ a 2 c 2

.

.

.

a ₅ c ₅

R 1 R 2

.

.

.

R 5

-

1/2EE (-Di+j+ltijak alam(Akl i=1 j>i

-

^A km + ^A im )

где Ф у = (R i C j — C i R j ), а © j = (a i R j — R i a , ).

Получаем

। ।    4 P 4=1 P 5 >i ^{( — 1) i + j +1} Ф у A ki A km A im     55d³S ³

^{| Z 1} | =--------------- A---------------- 2 a

| z 2 |

4 EL1 E^H)^ A kl A km A im | A |

55d ³ S ³

^- 2 | A |

| z 5 |

^— 2 P 4-1 P 5> г ^{( — 1) i + j +1} ® ij c k ^c l ^c m ^(A kl ^{— A} km + ^A lm )    155d 6 S

| A |                                    ^- | A |

— 2 Pi=1 P5>i( — 1)i+j+1Фijakalam(Akl — Akm + Alm)    155d6S iA              -ПдГ

Теорема доказана.

Как следствие, получается следующее утверждение.

Теорема 2. Пусть f (x,y) G C ³ (D) . Обозначим

M 3 = max x,y ∈ D

d ³ f(x,y) ∂x ³

| , | ^d 3 f(^xr^y2 |.l ∂x ² ∂y

d ³ f (x,y) ∂x∂y ²

d ³ f (x,y) ∂y ³

Тогда, в обозначениях теоремы 1, выполняются следующие оценки:

df (х о ,У о ) p     dx	5^M 3 d 4 S 3 -       6 | A|     ,	df (x o ,y o ) q - ∂y	5V2M 3 d 4 S 3 -      6 | A |
d 2 f (х о ,У о ) a      dx 2	5 V 2M 3 d 7 S -       | A |       , в — d 2 f ( x o ,y o ) dxdy	d 2 f(x o ,y o ) <5 ^ 2M 3 d 7 S 7      dy 2      -      | A | 5 V 2M 3 d 7 S -        | A |       .

Изучим возможность аппроксимации вторых производных для функций классов C2(D) и C2,a(D). Пусть функция f (x,y) G C2(D) и ^(t) — модуль непрерывности второго дифференциала. Другими словами, имеет место неравенство для любой пары точек p, q ∈ D kdp — dqk- ^(|p — q|).

Имеет место

Теорема 3. Пусть f (x,y) G C ² (D) и ^(t) — модуль непрерывности второго дифференциала этой функции. Предположим, что точки p 0 , p 1 , ..., p 5 выбраны как в теореме 1. Тогда справедливы неравенства для оценок производных в теореме 1 с

δ ≤

d ²

dτ

₀ dτ ₀

u(t)dt.

Доказательство. Пусть точка p Е D такая, что отрезок p ₀ p С D. Согласно цепному правилу для t Е [0,1],

^ 2 f ⁽P o + ^t(P - P o )) = d p o + t ( p - p o ) f ⁽P ^- P o ,P ^- P o ).

Проинтегрируем данное равенство по t от 0 до некоторого значения т Е [0,1]. Получим равенство dPo+т(p-po)f(P - Po) - dpof(P - Po '

τ

= У ^d P ₀ + t ( p - p ₀ ) f⁽P ^- P o ,P ^- P o ) ^{- d} P 0 f⁽P ^- P o ,P ^- P o ^{) dt} + ^Td p ₀ f⁽P ^- P o ,P ^- P o ). o

Теперь проинтегрируем полученное равенство по т от 0 до 1. Приходим к равенству

f ⁽P) ^- f ⁽P o ) ^- d p o f⁽P ^- P o ) =

1 T

=/ ^dT /

^d P o + t ( p - P o ) f⁽P — P o ,P ^- P o )

^{- d}p₀ f⁽P ^- P o ,P ^- P o ^{) dt} +

+ |^d p 0 f⁽P ^- P o ,P ^- P o ).

Учитывая модуль непрерывности второго дифференциала и делая замену переменных в повторном интеграле, получаем неравенство

| f (P) ^- f (P o ) ^{- d} P 0 f⁽P ^- P o ) ^- 2^d p 0 f⁽P ^- P o ,P ^- P o ) | <

Таким образом,

≤

| p - p 0 |       τ

Z ^dT Z

u(t)dt.

δ ≤

dτ dT {

u(t)dt,

и, тем самым, теорема доказана.

Следствие. Пусть f (x,y) Е C ^{2 ,a} (D) и ^(t) — модуль непрерывности второго дифференциала этой функции. Предположим, что точки P _o ,P 1 , ...,P 5 выбраны как в теореме 1. Тогда справедливы неравенства для оценок производных в теореме 1 с

α

δ ≤

T^TfkCA k f k c ² " (а + 1)(а + 2)

где Ilf 11c 2.™

sup p ⁰ ,p ⁰⁰ ∈ D

k d po f - d p oo f k k p ⁰ - p ⁰⁰ k

Теперь мы сможем сделать вывод о том, что для аппроксимации вторых производных наиболее существенной величиной является величина А. Заметим, что эта величина равна нулю, если и только если шестерка точек P i , i = 0,..., 5, лежит на какой-либо кривой второго порядка. В следующем параграфе мы вычисляем эту величину для некоторых видов расположения таких точек.

2.    Вычисление величины |А| для некоторых классов шестиугольников

Рассмотрим два вида шестиугольников, таких что для первого выполнено У 1 = У 5 , У 2 = У 4 , Х о = Х з = 0, Х 1 = Х 2 , Х 4 = Х 5 , а для второго - У 1 = У 5 ,

• У2 = У4, Хо = Хз = 0.

3.    Искажение треугольников

Теорема 4. Обозначим величину | А | для первого вида шестиугольников как | А _i | , а для второго — как | А ₂ | . Тогда

^{| А} i ^| = — h i ^h 2 ^(T i + ^т 2 + ^T 3 ^{)( h} i + h 2 ) 2 (3^T 1 ^T 22 ^{- 4т} 1² 7 2 + ^т 2^{2 т} з )^,

| А 2 1 = :1 h 1 h 2 (T i + Т 2 + Т з )т 2 (т з (h^ - Т 1 (h i + h 2 ) ² ) -

- h2Ti(4Tihi + 2T2hi + T2h2)), где hi = |xi|, h2 = |x4|, Ti = |yi|, T2 = |y2 - yi |, тз = |уз - y21.

Теперь изучим вопрос, каким образом преобразуется величина А при квазиизометрии области D. Для выяснения ответа на него необходимо изучить вопрос искажения площадей треугольников при квазиизометриях, поскольку, как мы видели выше, величина А выражается через площади треугольников.

Предположим, что на евклидовой плоскости задан треугольник Р = (P ₀ ,P _i ,P ₂ ). Определим величину

^(Р) = min

^|P 0 ^{- P} i ^| + ^{| P} i ^{- P} 2 ^| | P ₀ - P ₂ |

^|P i ^{- P} 2 ^{| + | Р} 2 ^{- Р} 0 |   ^|P 2 ^{- Р} 0 | ^{+ | P} 0 ^{- P} i ^|

| P 1 - P 0 |         ^,          | P 1 - P 2 |

В силу неравенства треугольника выполнено неравенство ^(Р) >  1, причем треугольник является вырожденным тогда и только тогда, когда ^(Р) = 1. Пусть а обозначает минимальный угол в этом треугольнике.

Лемма 1. Имеет место соотношение cos а

< ^(Р) <  1 + 2 sin 02.

Доказательство. Обозначим через a ≤ b ≤ c длины сторон данного треугольника. Очевидно, что ^(Р) = (a + b)/c. Так как сторона c максимальна, то минимальный угол в треугольнике образуется стороной c и стороной b. Угол между сторонами c и a обозначим через β ≥ α. Тогда c = b cos а + a cos в A (a + b) cos a, откуда получаем первое из нужных соотношений.

Пусть теперь d — это высота, опущенная на сторону c. Тогда

^(P ) =

d/ sin a + d/ sin в d/ tan a + d/ tan в, и, учитывая, что при α ≤ β ≤ (π - α)/2 производная

µ _β

sin α(1 - cos α cos β)    _{≥ 0}

(cos a sin в + sin a cos в)2 — ’ получаем sin α + cos α/2 µ(P) ≤                            = 1 + 2 sin α/2.

cos α cos α/ 2 + sin α sin α/ 2

Лемма доказана.

Замечание. Оценки, полученные в лемме, являются точными. При α = 0 обе части двойного неравенства равны 1, а в другом крайнем случае при α = π/ 3 обе части равны 2. Отметим также, что другие оценки искажения минимальных углов треугольников можно найти в монографии В.М. Миклюкова [3].

Предположим, что задано два треугольника P = (P0,Pi,P2) и P = (P0, P1, P2), причем l|Pi-Pj| ≤ |Pi0 - Pj0| ≤ L|Pi - Pj|.

Обозначим через α, α0 минимальные углы в этих треугольниках. Несложно получить следующие неравенства:

1 + 2 sin ^{α 0} ≥ ^{l 1} ,

2 L cos α

1 + 2 sin ^α ≥ 2

l 1

L cos α ^{0 .}

Действительно, пусть a ⁰ ≤ b ⁰ ≤ c ⁰ — длины сторон треугольника P ⁰ и a, b, c — соответствующие стороны треугольника P . Тогда, в силу леммы,

1 + 2 sin ^α ₂ ≥ µ ( P ⁰ ) =

a ⁰ + b ⁰ c ⁰

≥

la + b l

≥ _{L c} ≥ _Lµ ( P ) ≥

l 1

L cos α ^.

Второе неравенство доказывается аналогично. Используя эти неравенства, получим следующее утверждение об искажении площадей треугольников.

Лемма 2. Если S и S0 обозначают площади треугольников P и P0 соответственно, а угол α удовлетворяет условию l1

L cos α

≥ 1 + σ >  0 ,

то

1 „

S ≤ S0 ≤ Sν, ν где

и

ν = max

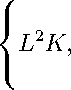
K l2Vi - (L )2(i+r

K = max { , σ

■ _;

' 1 - (L to

} ,

K lL(1+ Т)^1 - (L)2

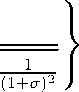
Доказательство. Из условий леммы и доказанных неравенств непосредственно получаем

Учитывая, что α, α ⁰ ≤ π/ 3, получаем

2 sin α cos α ≥ σ cos α .

Теперь, поскольку

то

Поэтому, из неравенства

будем иметь

sin α ⁰ ≥ σ sin α.

l 1

≥ 1 + σ, L cos α

sin α ≥

²       1

(1+^) 2 .

l 1

cos α ⁰ ≥

~ L 1 + 2 sin 2

sin α ⁰ ≤

1 -

l A²

≤

^L) (1 + 2sin ^ay

<    V1 - ( L ) ²4

V¹ — ( lL )

Таким образом, мы показали, что

2     1

(1+ ^ ) 2

sin α.

sin α ≤ sin α ⁰ ≤ K sin α. K

Перейдем к оценкам площадей. Пусть a ≤ b ≤ c — стороны треугольника P , а a ⁰ ≤ b ⁰ ≤ c ⁰ — стороны треугольника P ⁰ . Рассмотрим первый случай, когда нумерация вершин треугольников такова, что стороне a соответствует сторона a ⁰ , стороне b соответствует сторона b ⁰ , стороне c соответствует сторона c ⁰ . В этом случае

S ' = acd sin a ' <  -ac sin aL 2 K = SL 2 K,

22     ^,

1              l ²          l ²

₂ ac sin α_K = S_K.

S ⁰ = ₂ a c ⁰ sin α ⁰ ≥

Таким образом, получаем

1 ² Sk <  s' <  sl²k.

Рассмотрим следующий случай, когда нумерация вершин треугольников такова, что стороне a соответствует сторона b ⁰ , стороне b соответствует сторона a ⁰ , стороне c соответствует сторона c ⁰ . В этом случае

S' = -a'd sin a' <  -bc sin aL²K <  SL²K.

А в силу равенства asinα = bsinβ, где β угол напротив стороны a, имеем

S ⁰ = ¹ a ⁰ c ⁰ sin α ⁰ ≥ ¹ bcsinα ^l = S ^l s^inα

2          2 K K sinβ

≥

^SK ^l

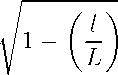
(1 + σ) ²

Рассмотрим следующий случай, когда нумерация вершин треугольников такова, что стороне a соответствует сторона c ⁰ , стороне b соответствует сторона a ⁰ , стороне c соответствует сторона b ⁰ . В этом случае

S ⁰ = a ⁰ c ⁰ sin α ⁰ ≤ ba sin αL ² K ≤ SL ² K.

Учитывая, как и выше, +a sin α = c, получаем

равенство a sin α = b sin β и неравенство 2a cos α ≥ b cos β+

S ⁰ = ₂a ⁰ c ⁰ sin α ⁰ ≥ ₂basinα_K ≥

≥ S

l ²      sin α

K 2 cos α sin β

≥ ¹₂S^l_K^L(1+σ)

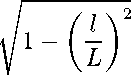
(1 + σ) ^{2 .}

Следовательно, окончательно получаем неравенство

1 „

S ≤ S0 ≤ νS, ν где

ν = max

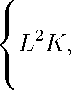
K lv1 - ( l .

K lL(1 + -^1 — (L )2^2

Лемма доказана.

4.    Оценка преобразования величины ∆ при квазиизометрии

Воспользуемся полученными оценками площадей для оценки искажения величины ∆ для шестиугольников описанных выше случаев. Рассмотрим шестиугольники P ₀ P ₁ P ₂ P ₃ P ₄ P ₅ и P ⁰ ₀ P ⁰ ₁ P ⁰ ₂ P ₃ ⁰ P ₄ ⁰ P ₅ ⁰ . Пусть выполняется условие l | P _i - P j | ≤ | P ⁰ _i - P _j ⁰ | ≤ ≤ L | P _i - P j | , i = 0, 5, i 6 = j . Обозначим через S _i ⁰ , S _i ≥ 0 слагаемые, участвующие в формуле для ∆, так, что

∆ = S 1 +...+S 6 - S 7 - ... - S 10 ,

∆ ⁰ = S ₁ ⁰ + ... +S ₆ ⁰ - S ₇ ⁰ - ... - S ₁ ⁰ ₀ .

Каждое такое слагаемое представляет собой произведение четырех площадей треугольников. Пусть α — минимальный угол во всех треугольниках вида P0 Pi Pj , причем l1 ≥ 1 + σ > 0.

L cos α

Пусть ν определена, как и выше, по величинам l, L, σ. Тогда _ν¹ ₄ S i ≤ S i⁰ ≤ S i ν ⁴ .

Поэтому

A0 > 4 (S i + ... + S ₆ ) - v ⁴ (S 7 + ... + S_w) >  A (1 - (v ⁴ + 1) S 7 ⁺ _д ⁺ S ¹⁰

Учитывая вычисления величины A, получаем следующую теорему.

Теорема 5. Имеет место неравенство

A0 > A     — (v4 + .)©) , где для первого вида шестиугольников о _ (Т1 + Т2) ((Т1 + Т2)2 + Т(Т1 + 2Т2 + Тз))

~           4 (3Т1Т22 - 4Т12Т2 + Т22Т3)       , а для второго –

О _ ^{( т} 1 ^{+ Т} 2 ) ( ^Т 1 (^Т 1 ^{+ Т} 2 ^{+ T} 3 ^)(h 12 ^{+ h} 2^{2 ) —} (^h 1 (^T 1 ^{+ Т} 2 ) ^{— h} 2 ^T 1 ^{) 2} ) "      4 Т 2 (Т з (h² 1 T 2 - T 1 (h 1 + h 2 ) ² ) - h 2 T 1 (4T 1 h 1 + 2T 2 h 1 + T 2 h 2 )) .