Геометрия комплексных чисел и кватернионов

Теории комплексных чисел, кватернионов относятся к небольшому числу фундаментальных частей геометрии, имеющих наиболее важные приложения в физике.

Рассмотрим на евклидовой плоскости систему ортонормированных координат. Точка плоскости представляется в виде a+bi .

zl = 1

Умножение на комплексное число z, такое что      , является поворотом плоскости на угол, равный arg z.

Новый вид чисел был обнаружен ирландским математиком Уильямом Гамильтоном в 1843 году, и он содержал не две, как ожидалось, а три мнимые единицы. Гамильтон назвал эти числа кватернионами.

Памятная табличка на мосту Брум Бридж в Дублине гласит: «Здесь на прогулке, 16 октября 1843 года, во вспышке гения, сэр Уильям Роуэн Гамильтон открыл формулу перемножения кватернионов».

Кватернион – это вектор 4-мерного вещественного пространства с базисом 1, i, j, k (которые называются базисными кватернионами): a+bi+cj+dk . Число а называется вещественной частью (скаляром), а трехмерный вектор v=bi+cj+dk – мнимой частью кватерниона. Слово «вектор» впервые появилось именно в этой теории.

ijk=-1.

Сопряженным к кватерниону q=a+v называется кватернион q a v q • q = a2 + ||v||2 > 0

.

Квадратом нормы кватерниона q называется число

Пусть дан кватернион с нормой единица,

q=a+v ,

II q = 1

.

a ² +1 M² = 1

Естественно принять:

a = cos ^ ,

II v = ^sin P    т.е.

q cos^ + sm ^ v , где v' - орт оСи. Вектор трехмерного пространства v‘ имеет норму единица.

В качестве ^Ф для построения кватерниона, описывающего поворот на угол ⁰ вокруг оси v' , нужно выбрать половину угла поворота, ^Ф = ⁰ /2 ,

Г о У

0 А q = cos - + sin|    "

12 )

V 2 )

• v .

Из-за двойки вращение определяет кватернион неоднозначно. Одному и тому же повороту отвечают два кватерниона (различающиеся знаком). Все кватернионы нормы 1 образуют сферу S3 в R4.

При отождествлении в одну точку каждой пары противоположных точек сферы Sn в евклидовом пространстве Rn+1 из сферы получается n-мерное гладкое многообразие, которое называется вещественным n-мерным проективным пространством и обозначается через RPn.

ixieHBai'MhM!

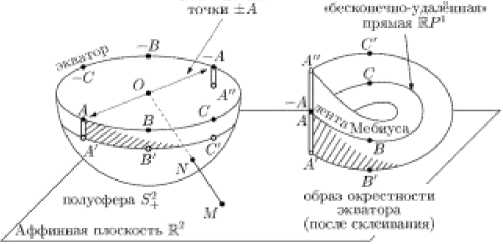
Пример. Проективная плоскость RP2 получается из аффинной плоскости  R2  добавлением «бесконечно-удалённой прямой» RP1, содержащей по одной бесконечно-удалённой точке на каждой прямой аффинной плоскости. Чтобы всё это ясно увидеть, можно начать, отождествляя противоположные точки не со всей сферы S2, а лишь с замкнутой полусферы S2 (скажем, южнее экватора). Тогда склеивать придётся только каждую точку А экватора с противоположной, -А, а открытая строго южная полусфера при склеивании не пострадает.

{ & } радиуса ^п

Совокупность всех таких вращений можно описать как шар

в

трехмерном евклидовом пространстве.

Поверхность, образованная комплексными решениями уравнения x ⁺ y = ¹, включая «бесконечно удаленные», оказывается сферой Римана, S²=CP¹.

Для других многочленов Н(х,у) получились бы другие поверхности Н=0, которые могут и не быть сферами. Например, уравнение 23

«эллиптической кривой» y = x x задает при почти всех Е поверхность тора S1xS1, называемого также «сферой с одной ручкой».

При замене показателя 3 в х3 более высоким показателем 2g+1 получается в качестве римановой поверхности сфера с g ручками. Число g называется родом поверхности.

Весь набор связных замкнутых гладких ориентируемых поверхностей исчерпывается сферами с g ручками (g = 0, 1, 2, …).