Геометрия пространств Карно - Каратеодори, квазиконформный анализ и геометрическая теория меры

Геометрия пространств Карно - Каратеодори, квазиконформный анализ и геометрическая теория меры

Автор: Водопьянов Сергей Константинович

Журнал: Владикавказский математический журнал @vmj-ru

Статья в выпуске: 1 т.5, 2003 года.

Бесплатный доступ

В настоящей работе приводятся результаты по геометрии пространств Карно - Каратеодори. Демонстрируется применение этих результатов для доказательства \Cal P-дифференцируемости липшицевых и слабо контактных отображений пространств Карно - Каратеодори. Показаны также некоторые применения теории дифференцируемости к геометрической теории меры и теории квазиконформных отображений на пространствах Карно - Каратеодори.

Короткий адрес: https://sciup.org/14318069

IDR: 14318069

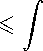
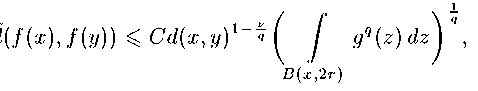
Список литературы Геометрия пространств Карно - Каратеодори, квазиконформный анализ и геометрическая теория меры

  • Водопьянов С. К. L_p-теория потенциала и квазиконформные отображения на однородных группах//Современные проблемы геометрии и анализа.-Новосибирск: Наука, 1989.-С. 45-89.
  • Водопьянов С. К. Монотонные функции и квазиконформные отображения на группах Карно//Сиб. мат. журн.-1996.-Т. 37, № 6.-С. 1269-1295.
  • Водопьянов С. К. О замкнутости классов отображений с ограниченным искажением//Математические труды.-2002.-Т. 5, № 2.-С. 91-136.
  • Водопьянов С. К., Грешнов А. В. О дифференцируемости отображений пространств Карно -Каратеодори//Докл. РАН.-2003.-Т. 389, № 5.-С. 1-5.
  • Водопьянов С. К., Грешнов А. В. Аналитические свойства квазиконформных отображений на группах Карно//Сиб. мат. журн.-1995.-Т. 36, № 6.-С. 1317-1327.
  • Водопьянов С. К., Грешнов А. В. O продолжении функций ограниченной средней осцилляции на пространствах однородного типа с внутренней метрикой//Сиб. мат. журн.-1995.-Т. 36, № 5.-С. 1015-1048.
  • Водопьянов С. К., Латфуллин Т. Г. Весовые пространства Соболева и квазигиперболические отображения на группах Карно//Комплексный анализ в современной математике. К 80-летию Б. В. Шабата.-М.: ФАЗИС, 2001.-С. 81-98.
  • Водопьянов С. К., Ухлов А. Д. Аппроксимативно дифференцируемые преобразования и замена переменных на нильпотентных группах//Сиб. мат. журн.-1996.-Т. 37, № 1.-С. 70-89.
  • Водопьянов С. К., Ухлов А. Д. Операторы суперпозиции в пространствах Лебега и дифференцируемость квазиаддитивных функций множества//Владикавк. мат. журн.-2002.-Т. 4, № 1.-C. 11-33.
  • Постников М. М. Группы и алгебры Ли.-М.: Наука, 1982.-447 с.
  • Решетняк Ю. Г. Пространственные отображения с ограниченным искажением.-Новосибирск: Наука, 1982.-278 с.
  • Решетняк Ю. Г. Соболевские классы функций со значениями в метрическом пространстве//Сиб. мат. журн.-1997.-Т. 38, № 3.-C. 657-675.
  • Хелгасон С. Дифференциальная геометрия и симметрические пространства. Т. I.-М.: Мир, 1964.-533 с.
  • Chernikov V. M., Vodop'yanov S. K. Sobolev Spaces and Hypoelliptic Equations. I//Siberian Advances in Mathematics.-1996.-V. 6, № 3.-P. 27-67.
  • Chernikov V. M., Vodop'yanov S. K. Sobolev Spaces and Hypoelliptic Equations. II//Siberian Advances in Mathematics.-1996.-V. 6, № 4.-P. 64-96.
  • Cheeger J. Differentiability of Lipschitz functions on metric measure spaces//Geometric and Functional Analysis.-1999.-V. 9.-P. 428-517.
  • Folland G. B., Stein I. M. Hardy spaces on homogeneous groups.-Princeton: Princeton Univ. Press, 1982.-274 p. (Math. Notes; 28)
  • Fanghua L., Xiaoping Y. Geometric measure theory.-Beijing-New York: Science Press, 2002.-237 p.
  • Federer H. Geometric measure theory.-Berlin: Springer, 1969.-676 p.
  • Gromov M. Carnot-Caratheodory spaces seen from within/In: Sub-Reimannian geometry.-Basel: Birkhauser, 1996.-P. 79-323.
  • Hajlasz P. Sobolev spaces on an arbitrary metric space//Potential Analysis.-1996.-V. 6.-P. 403-415.
  • Heinonen J. Lectures on analysis on metric spaces.-NY: Springer, 2001.-140 p.
  • Hormander L. Hypoelliptic second order differential equations//Acta Math.-1967.-V. 119.-P. 147-171.
  • Jerison D. The Poincare inequality for vector fields satisfying Hormander's condition//Duke Math. J.-1986.-V. 53, № 2.-P. 503-523.
  • Koranyi A., Reimann H. M. Foundations for the theory of quasiconformal mappings on the Heisenberg group//Adv. Math.-1995.-V. 111.-P. 1-87.
  • Lu G. Weighted Poincare and Sobolev inequalities for vector fields satisfying Hormander's condition and applications//Rev. Mat. Iberoamericana.-1992.-V. 8, № 3.-P. 367-439.
  • Lu G. The sharp Poincare inequality for free vector fields: An endpoint result//Rev. Mat. Iberoamericana.-1994.-V. 10, № 3.-P. 453-466.
  • Magnani V. Differentiability and area formula on stratified Lie groups//Houston Journal of Math.-2001.-V. 27, № 2.-P. 297-323.
  • Margulis G. A., Mostow G. D. The differential of quasi-conformal mapping of a Carnot -Caratheodory spaces//Geometric and Functional Analysis.-1995.-V. 5, № 2.-P. 402-433.
  • Martio O., Maly J. Luzin's condition (N) and mappings of the class W^{1,n}//J. Reine Angew. Math.-1995.-V. 485.-P. 19-36.
  • Mitchell J. On Carnot -Caratheodory metrics//J. Differential Geometry.-1985.-V. 21.-P. 35-45.
  • Montgomery R. A tour of subriemannian geometries, their geodesics and applications.-Providence: American Mathematical Society, 2002.-260 p.
  • Mostow G. D. Strong Rigidity of Locally Symmetric Spaces//In: Annals of Mathematics Studies, No. 78.-Princeton, N. J.: Princeton University Press; Tokyo: Tokyo Univ. Press, 1973.-195 p.
  • Nagel A., Stein E. M., Wainger S. Balls and metrics defined by vector fields I: Basic properties//Acta Math.-1985.-V. 155.-P. 103-147.
  • Pansu P. Metriques de Carnot -Caratheodory et quasiisometries des espaces symetriques de rang un//Ann. of Math.-1989.-V. 119.-P. 1-60.
  • Reshetnyak Yu. G. Some geometric properties of functions and mappings with generalized derivatives//Mat. Sb.-1966.-V. 7, № 4.-P. 886-919.
  • Rademakher H. Ueber partielle und totale Differenzierbarkeit. I//Math. Ann.-1919.-V. 79.-P. 340-359.
  • Pauls S. D. A notion of rectifiability modeled on Carnot groups.-Hanover, 2001.-21 p. (Preprint, Dartmooth College, http://hilbert.dartmooth.edu/~pauls/preprin4.html).
  • Stein E. M. Harmonic Analysis: Real-Variables Methods, Orthogonality, and Oscillatory Integrals.-Princeton: Princeton Univ. Press, 1993.-695 p.
  • Stepanoff W. Ueber totale Differenzierbarkeit//Math. Ann.-1923.-V. 90.-P. 318-320.
  • Vodop'yanov S. K. \Cal P-differentiability on Carnot groups in different topologies and related topics//Труды по анализу и геометрии (Редактор-составитель С. К. Водопьянов).-Новосибирск: Изд-во ИМ СО РАН.-2000.-P. 603-670.
  • Vodop'yanov S. K. Sobolev classes and quasiconformal mappings on Carnot-Caratheodory spaces//In: Geometry, Topology and Physics. Proceedings of the First Brazil-USA Workshop held in Campinas, Brazil, June 30-July 7, 1996/Editors: B. N. Apanasov, S. B. Bradlow, W. A. Rodrigues, K. K. Uhlenbeck.-Berlin-New York: Walter de Gruyter & Co.-1997.-P. 301-316.
  • Vodop'yanov S. K., Greshnov A. V. Quasiconformal mappings and BMO-spaces on metric structures//Siberian Advances in Mathematics.-1998.-V. 8, № 3.-P. 132-150.
Еще
Статья научная
QR-код для установки приложения SciUp Наведите камеру и скачайте бесплатное приложение SciUp