Геоморфометрия в науках о земле и экологии: обзор методов и приложений

При всей специфике и разнообразии методов конкретных научных дисциплин, изучающих ландшафты, природные экосистемы и строение Земли, геофизические факторы носят общезначимый характер для этих дисциплин. Одно из важнейших мест среди них занимает рельеф. Причина этому состоит не только в том, что рельеф является перерасп-ределителем влаги, тепла, света и литодинамических потоков, но еще и в том, что он сравнительно легко доступен измерению. Кроме того, если касаться почв, то все другие факторы почвообразования (климат, геология, время, организмы) по отношению к рельефу являются факторами рельефообразова-ния [8], то есть в той или мере находят отражение в данных о рельефе.

В науках о Земле рельеф не изучается только как поверхность Земли. Действительно, уже попытка рассмотреть направление течения воды по земной поверхности требует привлечения другого геофизического фактора – гравитационного поля Земли, – без которого это течение немыслимо. Рассмотрение связанной с рельефом пространственной изменчивости терморежима склонов неизбежно требует привлечения еще одного геофизического фактора – векторного поля солнечного излучения. Обобщая эти факты, можно заметить, что при рассмотрении роли и аспектов действия рельефа анализируется физически и математически двойная система “земная поверхность + векторное поле” [63], причем из множества геофизических векторных полей (магнитное, электрическое,…, излучение от каждой звезды) именно гравитация и солнечная радиация оказываются наиболее важными для изучения пространственной изменчивости ландшафтов.

При том, что характеристики многих компонент ландшафта (ресурсы воды, почв, флоры и фауны; верхняя часть земной коры и др.) оказываются тесно связаны с рельефом, возникает естественный вопрос: достаточно ли обычно используемых двух-трех характеристик рельефа (высоты, крутизны и экспозиции склонов) для описания всего многообразия форм рельефа и всех аспектов его влияния на ландшафты и экосистемы? – Анализируя этот вопрос, И.С. Эванс [32] отметил “очевидность синдрома “философского камня”, подразумевающего веру, что существо природы форм поверхности может быть выражено одним параметром”. И двух-трех параметров для этого явно недостаточно. В то же время, неколичественные методы описания рельефа (деление рельефа на “волнистый”, “слабоволнистый”, “бугристый” и т.п.) уже исчерпали себя, не будучи в состоянии ни дать новые содержательные ответы на вопросы о видах механизмов влияния рельефа на перераспределение влаги, тепла и т.д. (например, о механизмах связи памяти в ланд- шафтах с рельефом), ни ввести объективные классификации форм рельефа, ни дать методы обнаружения статистически достоверных связей между характеристиками рельефа и изучаемых компонент ландшафта. О большом интересе к количественным методам анализа рельефа, составляющим содержание геоморфометрии как науки о рельефе свидетельствует, например, библиография Р. Пайка [58] по геоморфометрии и ее применениям, насчитывающая тысячи ссылок.

Несмотря на это обилие источников, в подавляющем большинстве посвященных использованию геоморфометрии (а не ее развитию), число базовых, то есть не составных, количественных характеристик рельефа в экологии, почвоведении и геоботанике оставалось, по сути, ограничено шестью – к перечисленным выше трем добавлялись еще горизонтальная кривизна, вертикальная кривизна и площадь сбора. Классификации форм рельефа продолжали носить субъективный характер, опираясь на вещественное содержание этих форм – “интрузивные” и другие формы [17], – либо на субъективное деление форм рельефа, например, “по пожеланиям агробизнес-партнеров” [43], иногда с малоосмысленными статистическими процедурами усреднения [11], но не геометрические принципы, осознанные в классических работах как наиболее адекватные задачам этого рода [9]. Редкие исключения [5; 73] не создавали целостной картины, либо развивались в физике [16] и математике [3], не находя применений в исследованиях ландшафтов и экосистем.

В этих условиях важным моментом для приложений геоморфометрии в науках о Земле стало расширение набора базовых количественных характеристик рельефа в самой геоморфометрии, инициированное П.А.Шарым [63], а также развитие на основе расширенной системы этих характеристик классификаций форм рельефа, построенных по геометрическому принципу. Эти задачи решались как на базе интеграции результатов из ряда научных дисциплин (от физики и математики до физической географии и геоморфологии), так и введением нами новых характеристик рельефа [63; 65; 67], и далее – введением и изучением свойств основанных на них новых классификаций форм рельефа [19; 20; 67]. Разрабатывались также и новые методы применения расширенной системы характеристик рельефа для анализа связей рельеф-почва-растения в ландшафтах [24; 55; 66]; для расчета и построения карт-матриц характеристик рельефа, а также для проведения статистических сравнений характеристик ландшафта с ними автором статьи разработана программа “Аналитическая ГИС Эко” [64].

Целью настоящей работы является обзор как понятий, методов и величин геоморфометрии, так и ее применений для изучения ландшафтов и природных экосистем.

Понятия и методы геоморфометрии

Основным понятием в геоморфометрии является понятие морфометрической величины (МВ), то есть числовой характеристики рельефа, определенной в каждой точке карты, такой как высота, крутизна или ориентация (направление, экспозиция) склона. Формы рельефа есть площадные объекты, такие как бессточная депрессия, положение границ и площадь которой, вне зависимости от ее генезиса, могут быть точно определены наибольшей окаймляющей ее замкнутой горизонталью (изолинией высоты). МВ является частным случаем понятия морфометрической характеристики, такой, как площадь, объем или средняя глубина бессточной депрессии, которая относится не к определенной точке местности (то есть не является МВ), но ко всей депрессии.

Учитывая современное развитие математической теории поверхностей, то есть дифференциальной геометрии поверхностей [10] и топологии [1], кажется, на первый взгляд, естественным просто заимствовать достижения этих наук, не занимаясь разработкой методов геоморфометрии. Однако давно используемые в науках о Земле крутизна и ориентация (экспозиция) склонов [29; 48] отсутствуют в дифференциальной геометрии поверхностей и топологии, поскольку в них ана- лизируется поверхность, а не математически двойной объект “земная поверхность + векторное поле”. Первые важные понятия, расширяющие геоморфометрию как науку, возникли в почвоведении, где наиболее явны и существенны результаты влияния водных и литодинамических потоков и терморежима склонов на формирование и свойства почв: А. Аандал [25] – при изучении азота в почвах; Ф. Трёх [73] – при анализе и классификации пространственной изменчивости гидроморфизма почв. Известны и другие ранние попытки развития недостающих в физике и математике подходов, например, П.К. Соболевский [13] в геологии был очень близок к введению горизонтальной кривизны для разделения выпуклых и вогнутых отрогов холмов.

МВ могут характеризовать либо систему “земная поверхность + векторное поле”, либо саму поверхность (без учета геофизических полей), когда мы говорим о геометрических формах рельефа, то есть все МВ можно разделить на поле-специфичные и игнорирующие поля [63]. Далее, МВ в данной точке может описывать либо свойства ограниченной окрестности этой точки (локальные МВ), либо же для ее определения в точке требуется рассмотрение протяженных участков рельефа (нелокальные МВ). В последнем случае имеется два варианта. В первом рассматривается ограниченный участок планеты, и тогда нелокальная величина описывает в данной точке относительное положение этой точки в рельефе [70], например, площадь сбора описывает положение данного участка в бассейне. Во втором варианте рассматривается вся замкнутая поверхность планеты; тогда такие понятия, как бассейн, оказывается невозможно определить, но зато появляются новые возможности, например, определить соотношение числа вершин холмов, доньев депрессий и планетарных седловых точек [48]. МВ, отвечающие первому варианту, были названы региональными МВ, морфометрические величины, отвечающие второму варианту – глобальными или планетарными МВ [65]. Это дает возможность ввести непересекающиеся классы МВ и форм рельефа (табл. 1).

Дополнительно к этому, имеется класс B' глобальных поле-специфичных МВ и класс D' глобальных игнорирующих поля МВ [65].

Морфометрические величины классов A и B описывают поверхностный сток, терморежим склонов и т.п., в то время как МВ классов C и D описывают геометрические формы. При этом МВ класса A описывают, например, поверхностный сток локально (по свойствам малой окрестности точки), в то время как МВ класса B описывают его регионально, то есть по относительному положению точки в рельефе. Аналогично, МВ класса C описывают геометрические формы локально, а МВ класса D – регионально, по относительному положению.

Важная систематизация представлений о поверхностном стоке в геоморфометрии состоит в установлении связей между механизмами аккумуляции веществ, перемещающихся под действием силы тяжести по земной поверхности, и некоторыми формами рельефа, такими как отроги, террасы, притальвеговые и приводораздельные области. Имеется два механизма аккумуляции (основных), а также сноса, таких веществ: за счет их сближения в плане и за счет их относительного замедления в профиле склона (рис. 1).

В 1948 году А. Аандал [25] предположил, что 1-ый механизм аккумуляции описывается горизонтальной кривизной, а 2-ой – вертикальной кривизной земной поверхности (тогда еще не были найдены формулы для этих кривизн). П.А. Шарый доказал теоремы [63] о том, что при локальном описании рельефа кривизнами горизонтальная кривизна описывает первый механизм аккумуляции, а вертикальная кривизна – второй. Это явилось

Таблица 1. Классификация морфометрических величин и понятий [65]

Морфометрические величины	Локальные	Региональные
Поле-специфичные	Класс A	Класс B
Игнорирующие поля	Класс C	Класс D

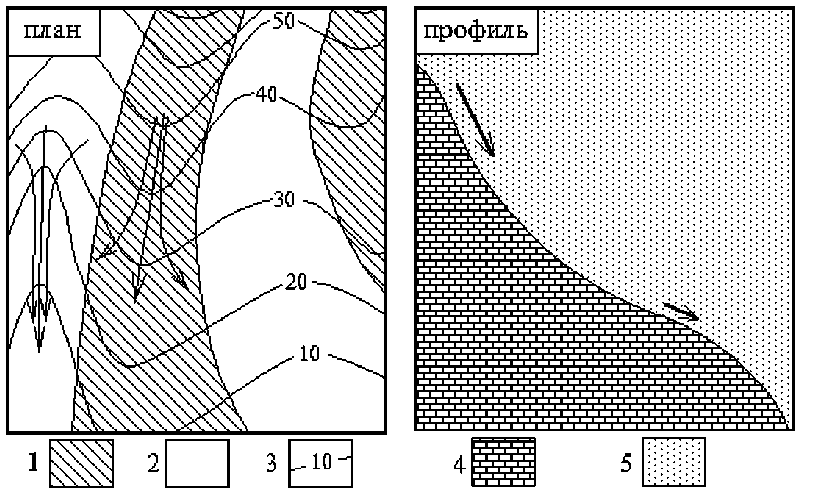
Рис. 1 . Слева – 1-ый механизм аккумуляции (за счет сближения линий тока в плане, эти перпендикулярные горизонталям линии показаны стрелками), изображена топографическая карта. Справа – 2-ой механизм аккумуляции (за счет относительного замедления потоков в профиле), показан разрез вдоль профиля склона. Условные обозначения: 1 – области дивергенции, 2 – области конвергенции, 3 – горизонтали, 4 – грунт, 5 – воздух

основанием для аргументированного использования этих МВ как описывающих механизмы аккумуляции.

Аандал [25] определил области с отрицательной горизонтальной кривизной kh (области конвергенции, рис.1) как вогнутые отроги, а области с положительной kh (области дивергенции) как как выпуклые отроги, области с отрицательной вертикальной кривизной kv как вогнутые террасы, а области с положительной kv как как выпуклые террасы.

На рис. 2 показаны карты kh и kv для одной и той же местности, отвечающие ее отрогам и террасам.

Наиболее популярными алгоритмами расчета локальных МВ по матрице высот земной поверхности являются метод Эванса-Янг [32; 72], метод Шарого [63] и метод Зевен-бергена-Торне [79]; сравнение их дано в работе [61]. Для расчета кривизн предпочтителен разработанный нами модифицированный метод Эванса-Янг [65], так как он существенно меньше выделяет артефактные направления на картах кривизн при расчете по матрице высоты [61].

При региональном описании 1-го механизма аккумуляции, т.е. при описании его по относительному положению точки в рельефе, используется площадь сбора MCA, рис. 3.

Площадь сбора показывает всю гидросеть местности – как реализованную, то есть реки и водоемы, так и потенциальную, то есть сухие долины и временные водотоки [67]. Алгоритм ее расчета опубликован в работах [46; 35].

Основные аспекты действия рельефа можно систематизировать следующим образом [67]:

• (1)    поверхностный сток сыпучих и жидких веществ,

• (2)    расчлененность (изрезанность) местности,

• (3)    геометрические формы (связанные памятью в ландшафтах),

• (4)    терморежим склонов,

• (5)    высотная поясность.

Помимо этих основных аспектов, действие рельефа проявляется еще в ряде более частных, специфических для конкретной местности, явлений (соответственно, менее общего характера), таких как описанная для бассейна р. Меконг во Вьетнаме [37] резкая зависимость свойств почв от высоты при перепаде высот около 1,2 м на участке размером ~50км х 100км, связанная с тем, что высота над уровнем моря на этой равнинной

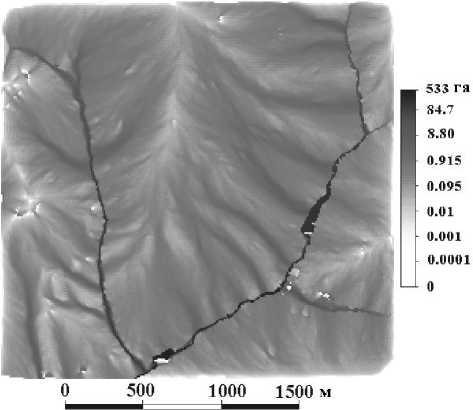
Рис. 3. Карта площади сбора для той же местности, что на рис. 2. Черные участки показывают реки

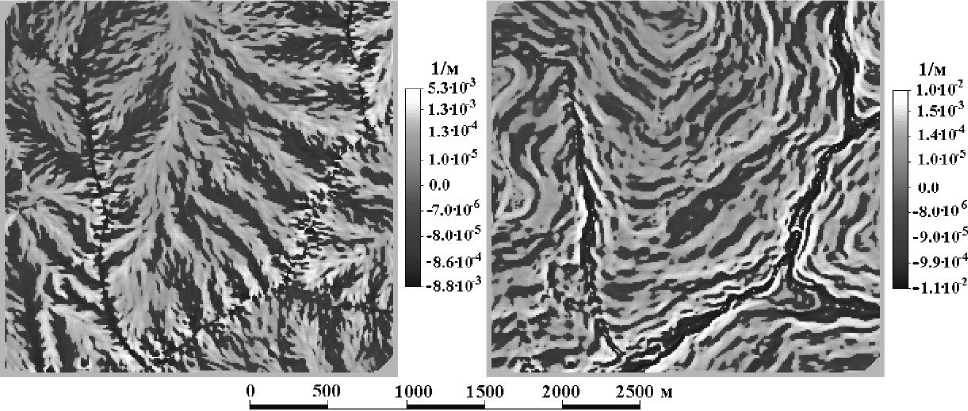
Рис. 2. Карты отрогов ( kh , слева) и террас ( kv , справа) Аандала для одной и той же местности, участка Данки, рассчитанные по матрице высот с шагом решетки 10 м. Эти формы рельефа отвечают двум механизмам аккумуляции, описанным на локальном уровне. Вогнутые отроги и террасы показаны темным, выпуклые – светлым

прибрежной территории есть одновременно и глубина до грунтовых вод. С.С. Неуструев [9] отмечал связь микроклимата некоторых местностей с рельефом, особенно заметную в горных странах, где в долинах наблюдается более контрастный микроклимат – зимой там застаивается холодный воздух с гор, а летом они сильно прогреваются. Описанный В.М. Фридландом [18] для Кавказа ряд частных примеров связи потоков воздушных масс с рельефом, таких как отсутствие лесов из-за открытости участка местности северным ветрам по условиям рельефа или изменения увлажнения почв из- за турбулентности ветров в предгорной равнине, также следует относить к неосновным аспектам действия рельефа. Проблема связи микроклимата в рельефом изучена пока явно недостаточно [31].

Система морфометрических величин

Система базовых МВ представлена в табл. 2. Отметим, что ориентация (экспозиция) склонов, крутизна и освещенность склонов зависимы между собой [67], т.к. эти три МВ зависят от двух частных производных; Н.М.Сибирцев [12] отмечал, что терморежим склонов характеризуется перпендикулярностью падения солнечных лучей на земную поверхность, а потому зависит как от ориентации, так и от крутизны склонов. Освещенность склонов непосредственно описывает эту перпендикулярность [67], а потому значительно лучше описывает терморежим склонов, чем их ориентация.

Физический смысл и формулы каждой из приведенных в табл. 2 МВ описаны нами в работах [65; 67], здесь мы не останавливаемся на этом.

К перечисленным здесь МВ следует добавить глубины бессточных депрессий и высоты В-холмов (буква В здесь означает класс); под последними понимаются холмы, возвышенности, горные системы и т.п. Вне депрессий (холмов) эти МВ полагаются равными нулю [65].

Таблица 2. Система базовых морфометрических величин

№п Название МВ (обозначение)		Что описывает	Источник	Класс
МВ, ОПИСЫВАЮЩИЕ ПОВЕРХНОСТНЫЙ СТОК
0	Ориентация склонов ( A 0 )	Направление потоков	--	А
1	Крутизна склонов ( GA )	Скорость потоков	--	А
2	Горизонтальная кривизна ( kh )	1-ый механизм аккумуляции	Й.Крхо [40]	А
3	Площадь сбора ( MCA )		Дж.Спейт [69]	В
4	Дисперсивная площадь ( MDA )		Дж.Спейт [70]	В
5	Вертикальная кривизна ( kv )	2-ой механизм аккумуляции	И.С.Эванс [32]	А
6	Разностная кривизна ( E )	Сравнивает 1-ый и 2-ой механизмы аккумуляции	П.А.Шарый [63]	А
7	Полная аккумуляционная кривизна ( KA )	Выявляет зоны относительной аккумуляции	П.А.Шарый [63]	А
МВ, ОПИСЫВАЮЩИЕ РАСЧЛЕНЕННОСТЬ РЕЛЬЕФА
8	Полная кольцевая кривизна ( KR )	Извилистость потоков (расчлененность рельефа)	П.А.Шарый [63]	А
9	Горизонтальная избыточная кривизна ( khe )	Эти две МВ расщепляют извилистость потоков на две компоненты	П.А.Шарый [63]	А
10	Вертикальная избыточная кривизна ( kve )		П.А.Шарый [63]
11	Ротор ( rot )	Направление поворота линий тока	П.А.Шарый [22]	А
МВ, ОПИСЫВАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФОРМЫ РЕЛЬЕФА
12	Несферичность ( M )	Отличие формы рельефа в точке от сферической	П.А.Шарый [63]	С
13	Средняя кривизна ( H )	«Равновесную» (минимальную) поверхность, имеющую минимальную при данной границе площадь.	Т.Юнг [77]	С
14	Максимальная      кривизна ( kmax )	Гребневые формы рельефа	--	С
15	Минимальная кривизна ( kmin )	Килевые формы рельефа	--	С
16	Полная гауссова кривизна ( K )	Не меняется при изгибании Поверхности	К.Ф.Гаусс [3]	С
МВ, ОПИСЫВАЮЩИЕ ТЕРМОРЕЖИМ СКЛОНОВ
17	Освещенность склонов ( F )	Интенсивность      прямого солнечного излучения	--	А
МВ, ОПИСЫВАЮЩИЕ ВЫСОТНУЮ ЗОНАЛЬНОСТЬ
18	Высота земной поверхности ( z )	Изменение температуры и давления атмосферы	--	А

Классификации форм рельефа

Первая классификация форм поверхности предложена К.Ф. Гауссом [3], она основана на знаках полной гауссвой кривизны и средней кривизны – МВ, описывающих геометрические формы. В ней 4 типа форм. Позднее Ф.Р. Трёх [73] предложил иную классификацию форм рельефа, основанную на знаках горизонтальной и вертикальной кривизн, отвечавшую двум основным механизмам аккумуляции. В ней также 4 типа форм. П.А. Шарый [63] предложил более общую классификацию форм рельефа, включавшую в себя классификации Гаусса и Треха как частные случаи. В этой классификации 12 типов форм. Свойства этих классификаций, а также соотношения между ними изучены нами в работах [19; 20; 63; 67]. Классификации Гаусса и Трёха показаны на рис. 4.

Нами доказано [63], что каждый из этих типов форм является составным, т.е. составлен несколькими типами форм рельефа классификации Шарого. Типы форм последней показаны на рис. 5.

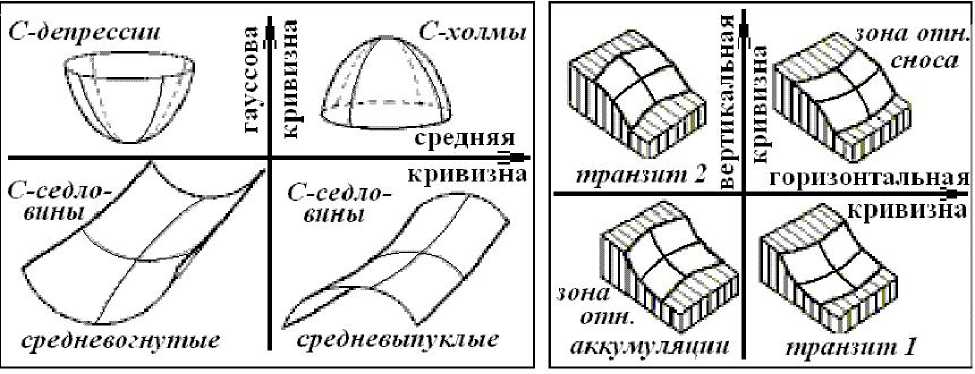
Рис. 4. Слева – типы форм рельефа классификации Гаусса, справа – типы форм рельефа классификации Трёха

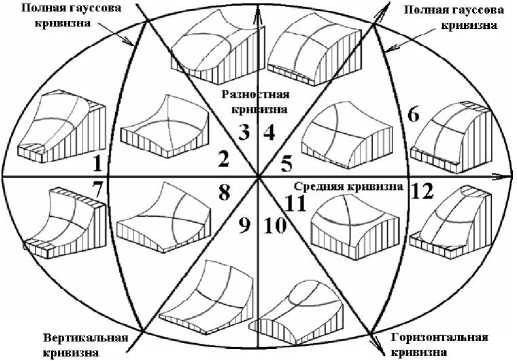
Рис. 5. Двенадцать типов форм рельефа классификации Шарого. См. подробнее работу [20]

Помимо этих (основных) типов форм рельефа, можно определить еще редкие типы форм, образующих на картах линии или точки, обычно общие границы соседних основных типов форм [63]. Примеры редких типов форм показаны на рис. 6.

При расчете по матрицам высот вероятность встретить такие редкие формы чрезвычайно мала, то есть в частоте встречаемости редких и основных форм рельефа имеется природная иерархия [63]. Это проверено нами экспериментально [19]. Во многих работах, начиная с работы Ю.К. Ефремова [5], нет этого важного различения основных и редких типов форм.

Большее число типов форм в классификации Шарого, по сравнению с классификациями Гаусса и Трёха, означает и большую гиб-

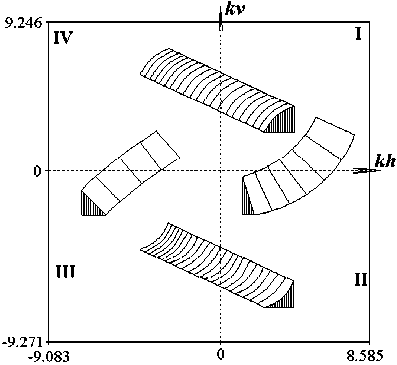
Рис. 6. Примеры редких типов форм, показанных на плоскости, по осям которой отложены горизонтальная кривизна kh и вертикальная кривизна kv : I – рассеивающие с идеально прямым профилем ( kv =0); II – замедляющая с идеально прямыми горизонталями ( kh =0); III – собирающие с идеально прямым профилем ( kv =0); IV – ускоряющие с идеально прямыми горизонталями ( kh =0) кость их использования. Так, В. Буивидайте и Г. Мозгерис [28] нашли при сравнении типологических единиц почв с основными типами форм этих трех классификаций наиболее тесную связь для классификации Шарого.

Описанные выше классификации форм рельефа относятся к локальным, то есть построенным с помощью локальных МВ. В силу негладкой природы земной поверхности [44] такие типы форм существенно зависят от масштаба карты [67], что создает заметные трудности при их использовании.

Эти трудности, однако, в гораздо мень- шей степени свойственны региональным классификациям форм рельефа. Наиболее явно это проявляется при использовании для классификации бессточных депрессий и В-холмов. Общая предложенная нами региональная классификация основана на доказанном положении [67], что границы этих форм рельефа не могу пересекаться, хотя одна из них и может находиться внутри другой (например, горное озеро – внутри горной системы, или наоборот – остров в озере). Это дает разделение всего рассматриваемого региона на В-холмы, бессточные депрессии и пространство между ними, которое можно назвать В-седловинами.

Проблема негладкости земной поверхности

Негладкость (то есть недифференцируемость) земной поверхности проявляется в том, что за попытку рассчитать несуществующие производные методом конечных разностей мы “платим” неустранимой зависимостью полученных дифференцированием высоты по плановым координатам локальных МВ от масштаба карты или шага решетки матрицы [33; 67]. Хотя в России до наших исследований использовались только такие МВ, мнение о том, что все МВ локальны [7; 11] следует признать ошибочным. Неглад-кость земной поверхности приводит к целому ряду важных следствий, изученных нами в работе [67], среди которых есть и то, что основанные на использовании производных выше второй степени МВ вообще не дают содержательных карт, вопреки известной в стране “парадигме Ласточкина” [7], где они фигурируют, но либо просто ошибочны (например, водораздел невозможно выразить через производные, т.к. граница бассейнов – понятие региональное), либо никогда не проверялись на практике расчетами и построением карт для реальных местностей.

В то же время, как экспериментально и теоретически показано в наших исследованиях [65; 67], для ряда региональных МВ проблема зависимости МВ от масштаба имеет решения. То есть, для таких МВ существуют предельные значения при укрупнении масштаба, а значит, здесь применимо поня- тие точности в значениях МВ, в том же смысле, что и в геодезии для высоты.

Использование геоморфометрии в науках о Земле и экологии

Разумеется, рельеф не является единственным фактором, от которого зависят характеристики ландшафта, такие как свойства почв или растительности. Уже по этой причине выявление связи характеристик ландшафта с рельефом носит характер поиска статистических связей (или их отсутствия), с обязательным установлением статистической достоверности найденных связей. В неколичественных или полуколичественных исследованиях эта достоверность часто не устанавливается, и результаты носят скорее характер непроверенных гипотез, нередко основанных на одностороннем анализе рельефа, например, с помощью только одной МВ.

Так например, И.Н. Степанов [14] использовал знак горизонтальной кривизны для построения почвенных карт любого масштаба в своем “методе пластики рельефа”, неявно предположив тем самым, что первый механизм аккумуляции во всех случаях доминирует над вторым; статистическая достоверность этого им установлена не была. Этот подход подвергся справедливой критике со стороны других почвоведов [4]. Е.А. Гарши-нев и Б.П. Петрюк [2] использовали вертикальную кривизну для различения эрозионных и эрозионно-аккумулятивных земель. Ни роль этой характеристики рельефа по отношению к процессам в почвах и ландшафте, ни статистическая достоверность связи отмеченного авторами различия земель с этой характеристикой рельефа ими не устанавливались. Такая гипотеза противоречит прямым наблюдениям на пашне с помощью естественного радиоактивного цезия-137 растровой картины пространственной изменчивости чистой эрозии [42]; как видно из приведенного там “трехмерного” рисунка, водная эрозия связана как с первым, так и со вторым механизмами аккумуляции. Примеры этого рода можно продолжить; сосредоточимся, однако, на более успешных результатах.

Г. Синаи с соавт. [68] нашли высокий коэффициент корреляции (r=+0,90) между лапласианом высоты DDZ и влажностью почв в климатических условиях Израиля. Долгое время причины оставались непонят-нымы, хотя результат явно привлек внимание исследователей. В работе [50] не было найдено значимой корреляции между крутизной склонов и продуктивностью пшеницы, но она оказалась значимой между AZ и продуктивностью пшеницы и кукурузы [71]. Затем нами было установлено, что AZ «0 -2H , где H есть средняя кривизна [65]. Поскольку H=1/2(kv+kh) [63], то причина состоит в том, что H с равными весами описывает оба механизма аккумуляции, оказываясь отрицательной в зонах относительной аккумуляции и положительной – в зонах относительного сноса Трёха (рис. 4, справа). Значение r=+0,90 показывает, что влага в опыте Синаи с соавт. [68] была увеличена в зонах относительной аккумуляции. Эти авторы показали также сильное увеличение продуктивности пшеницы в этих зонах. Опыты по изучению связи влажности почв с микрорельефом были продолжены в наших исследованиях [6]. В гу-мидных климатических условиях юга Московской области на хорошо выраженном рельефе (овраг) было показано при шаге решетки w=3м, что коэффициент корреляции r = – 0,89 для связи относительной влажности серых лесных сильно смытых почв со средней кривизной. Почва оказывалась более влажной в зонах относительной аккумуляции. При этом коэффициенты корреляции влажности с kv и kh (взятыми порознь) в тех же точках оказались меньше, чем с H.

Л. Ланион и Г. Холл [41] рассчитывали зоны относительной аккумуляции Трёха (kh и kv) и крутизну склонов и использовали дискриминантный анализ для оценки потенциальной неустойчивости почв (определения мест начала оврагообразования). Помимо рельефа, они учитывали также материнские породы и терморежим склонов. Они нашли, что наиболее тесной является связь мест начала оврагообразования, тестировавшихся авторами экспериментально, с зонами относительной аккумуляции.

Л. Мартз и Е.де Джонг [47] изучали связь рельефа с пространственной изменчивостью естественных радионуклидов в почвах участка Канадских Прерий. В этом исследовании статистически значимая (при P<0,05) корреляция концентраций радионуклидов в почве с крутизной не была обнаружена, в отличие от корреляции с высотой, kh и kv. Эти авторы анализировали также причины увеличенного содержания песка в бессточных депрессиях, и пришли к заключению, что это вызвано ветровой эрозией, которая перемещает песок на сравнительно небольшие расстояния “прыжками и скачками”, в отличие от мелкодисперсных фракций почв, которые ветровая эрозия вначале размещает сравнительно равномерно по территории, а затем они перемещаются поверхностным стоком (водной эрозией) в притальвеговые области, где авторы наблюдали значительное увеличение их содержания.

А. Хаирстон и Д. Григал [36] статистически сравнивали крутизну, ориентацию склонов и одну из характеристик относительного положения в рельефе (длину склона) со свойствами почв и древесной растительности на пологом рельефе в песчаных почвах, покрытых дубовым лесом. Характеристики почв отбирались из четырех холмов, по 4 спускающихся с вершины холма, каждый на одной почвенной картографической единице, трансекты на каждом (ориентация трансект подбиралась СВ, ЮВ, ЮЗ, СЗ), каждый трансект на одном типе растительности, по 3 точки на каждой трансекте – в верхней, средней и нижней части склона. Измерялись ряд свойств почв и лесотаксационные характеристики. Для сравнения данных в 48 точках использовалась статистическая методика ANOVA. Наиболее тесная статистическая связь наблюдалась с характеристиками относительного положения в рельефе (P<10– 3), значима также была связь с ориентацией склонов (P<0,04). Связь остальных характеристик почв и растительности с рельефом почти не была статистически достоверной, за исключением Сорг (P<0,01) и полного N в почве (P<10–3) с относительным положением, а также полного N в лесной подстилке с ориентацией (P<0,03). Значимой корреляции характеристик растительности с рельефом не было найдено. Эти, в заметной мере отрицательные, результаты связаны, возможно, с не-учетом зон аккумуляции на склонах холмов, связанных с их вогнутостью или выпуклостью.

Площадь сбора играет немалую роль при описании рек вместе с потенциальной гидросетью [26; 27; 34; 35; 46; 47; 51; 53; 69], с ней статистически связаны водная обеспеченность почв и распространение растительности [60; 75], различные аспекты водной эрозии почв [34; 47; 51; 53] и ущерб от дождевых стоков [30], ряд параметров размывания дорог и неустойчивости склонов [56], условия возникновения рек [45], и она имеет важное значение при построении гидрологических моделей местности [27; 59], моделей уязвимости грунтовых вод от поверхностных загрязнений [38] и моделей зон водного пересыщения почв [56].

Здесь не рассматривается использование различных, часто некорректно определенных МВ, составленных из базовых МВ, см. о них, например, книгу [76].

Исследования по водной эрозии почв

В исследованиях водной эрозии почв рельеф играет особо важную роль, и в этой области разрабатывались достаточно серьезные физико-математические модели. Поэтому полезно рассмотреть историю этого вопроса с точки зрения использования в этих моделях геоморфометрии. В ранних зарубежных и во многих современных отечественных работах использовалось так называемое “универсальное уравнение эрозии” (USLE – от Universal Soil Loss Equation) вида E=R ⋅ K ⋅ LS ⋅ C ⋅ P, где E есть средняя потеря почв, R – фактор интенсивности дождя, K – почвенный фактор, LS – фактор рельефа (фактор длины склона в USLE), C – фактор растительного покрова и P – фактор превентивных практик. Однако, в 1991 году была осознана физическая бессмысленность длины склона, и было предложено заменить фактор LS (зависящий от крутизны и длины склона) на площадь сбора, имеющую ясный гидрологический смысл [57]. Новое уравнение стало известно как RUSLE, в нем

LS=A ⋅ MCAⁿGF^m, где MCA – площадь сбора, GF – фактор крутизны склонов (синус крутизны), A,m,n – числа, эмпирические коэффициенты. Модель RUSLE лучше отражает повреждение почв концентрированным водным потоком [54]. Дальнейшие исследования показали, что область применимости RUSLE весьма ограничена – эта модель применима лишь к участкам размером не более 100 метров без значимой кривизны склона и без значимого осаждения седимента [54]. Спустя два года после нашего исследования по выявлению смысла горизонтальной кривизны [23] полученные результаты, как и сама эта МВ (под названием “тангенциальная”), были пе-реокрыты американскими эрозионистами [52] и введены вместе с вертикальной кривизной и ориентацией склонов в новые модели эрозии, такие как USPED, SIMWE [53] или WEPP [34], позволявшие анализировать более сложные местности. Горизонтальная и вертикальная кривизны в моделях USPED и SIMWE, однако, использованы в виде их суммы, т.е. средней кривизны, что не позволяет оценивать относительную роль механизмов аккумуляции. Второй механизм аккумуляции описан только локально (сегодня еще не введена МВ для его регионального описания), и потому эти модели еще нуждаются в дальнейшем развитии. Тем не менее, отметим, что в них уже задействовано пять МВ, а менее детальное описание рельефа делает модели недостаочно эффеткивными.

Х. Митасова с соавт. [53] заключили, что при пространственно однородных осадках, почвах и растительности рельеф определяет на местности общий мало меняющийся “базовый узор” эрозии (то есть больше меняются показатели эрозии, чем этот узор), так что места относительно высокой эрозии остаются приурочены к современному рельефу. Это положение применимо и к моделям водного поверхностного стока, продемонстрированным на сайте авторов [53] цветным “трехмерным” фильмом.

Индикационный принцип

Большая трудоемкость и дорогивизна отбора и анализа образцов почв (или расти- тельности) делает совершенно нереальным измерения в сотнях тысяч или миллионах точек, необходимые для построения матрицы характеристик ландшафта. В таких случаях используют индикационные, внешние по отношению к почве характеристики, такие как рельеф, космоснимки, растровые измерения элекропроводности почв, сенсоры урожая сельхозкультур. Согласно результатам обзора [49], из этих данных наиболее информативным оказывается рельеф, являющийся к тому же одним из факторов почвообразования.

Индикационный принцип состоит в следующем: если некоторое свойство почв или растительности хорошо коррелирует с рельефом, то его можно прогнозировать прямо по рельефу [74]. На практике для этого осуществляются измерения данной характеристики почвы в количестве точек порядка 200 и проводится статистическое сравнение методом множественной регрессии этих характеристик со значениями МВ, рассчитанных в крупном масштабе, в тех же точках,. Если найдена статистически достоверная корреляционная связь, то полученные при сравнении коэффициенты корреляции используются для построения матрицы предсказанных значе- ний характеристик почв. Качество предсказания пространственной изменчивости почв проверяют сравнением предсказанных значений с измеренными в точках валидации значениями (для чего резервируется около 10% образцов почв – они не участвуют в регрессии) по известным критериям [49]. На рис. 7 показан пример результата расчета мощности гумуса по 143 точкам измерений в 120 тыс. точек с предсказанными в них значениями.

Интенсивные исследования этого рода за рубежом [39: 49; 60 и др.] привели к появлению ряда новых направлений в агрохимии и почвоведении, таких как прецизионное земледелие (районирование одного сельскохозяйственного поля для увеличения урожая), поиск земель с оптимальным плодородием, моделирование разнообразия экосистем и др. (см. [49]). Кроме того, полученные количественные характеристики пространственной изменчивости свойств ландшафтов и их большое значение для смежных с почвоведением дисциплин (например, гидрологии) привели к осознанию, что осуществляемая в настоящее время почвенная съемка не удовлетворяет запросам ее потребителей, в связи с чем в ряде стран разрабатываются новые критерии проведения

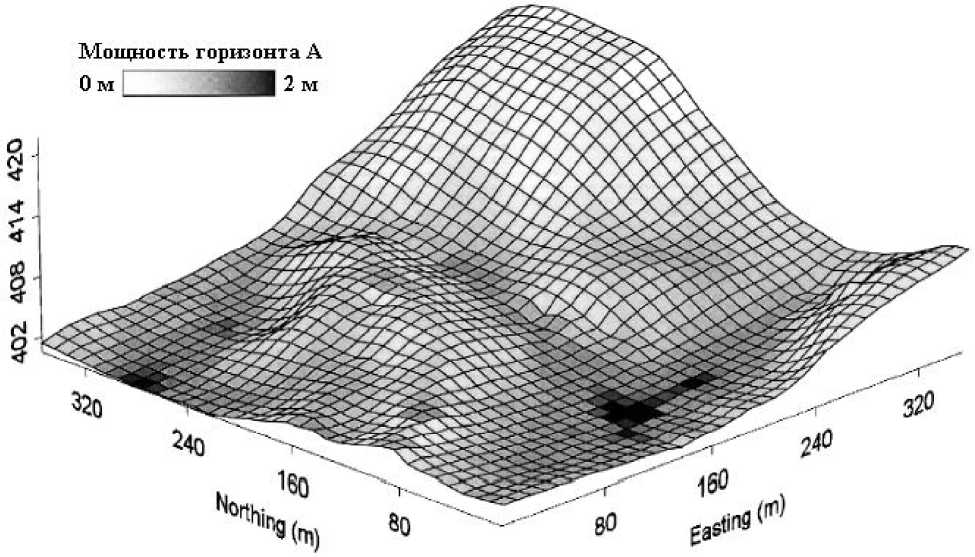
Рис. 7. Результаты предсказания пространственной изменчивости мощности горизонта А (гумусового) при шаге решетки w =10м [72], показанные на трехмерной диаграмме рельефа

этой съемки, более адекватные использованию количественных моделей.

Некоторые новые направления

Новые или ранее не использовавшиеся в данной области наук о Земле МВ, представленные в Табл.2, открывают и определенные новые, ранее недоступные возможности. Отметим в этой связи ряд таких недавно возникших направлений.

Память в ландшафтах, частный пример которой есть остаточные явления в почвах, концептуально известна [15]. Тем не менее, вопрос о связи почвообразования с рельефо-образованием оставался открытым. В наших исследованиях экспериментально [55] и теоретически [65] показано, что сравнение связи характеристик геометрических форм с характеристиками поле-специфичных форм является перспективным путем для выявления остаточных явлений в почвах и других проявлений памяти в ландшафтах.

Групповой анализ связи свойств ланд-щафта с рельефом, предложенный в наших исследованиях [24], можно сопоставить с обычно используемым фрагментарным анализом. В первом случае рассматривается весь набор МВ, для которых на конкретном участке выявляются дублирующие друг друга МВ (например, если крутизна возрастает вниз по склону, то она связана с высотой и может ее дублировать) и выделяются основные физические механизмы, определяющие связь свойств ландшафта с рельефом. При фрагментарном анализе те или иные МВ выделяются исследователем априорно, и связь их с характеристиками ландшафта в этом случае может не носить причинно-следственного характера.

Зоны аккумуляции в рельефе способны динамически аккумулировать переносимые с водными потоками мелкодисперсные частицы почв (ил, тонкая пыль, глина), изменяя в несколько раз характеристики почв и эколо-го-ценотических групп растительности. Новые методы геоморфометрии позволяют выявлять такие зоны аккумуляции (трудно обнаруживаемые по топокартам) и устанавливать закономерности изменения характерис- тик ландшафта в них [24; 66].

В агроландшафте при отсутствии корреляции продуктивности зерновых с рельефом нами установлена значимая корреляция с ним показателей качества урожая [24]. Как показано в наших исследованиях [21], модификация площади сбора для анализа распространения жидкого загрязнителя из одной или более точек позволяет рассчитать по рельефу максимальную область распространения жидкого контаминанта, например, нефти при аварийных разливах. Здесь становится очень существенной негладкость земной поверхности, вызывающая многократные разветвления и слияния потоков нефти. Реальная область распространения уже требует моделирования потерь нефти при ее латеральном переносе на впитывание в почву, испарение и химическое разложение. Методы этого рода перспективны для оценки связанных с латеральным переносом воды и жидких контаминантов экологических рисков, моделирования распространения удобрений на сельхозполях и др.

Новая расширенная система МВ и дальнейшее развитие геоморфометрии и ее приложений открывают новые возможности для изучения ландшафтов и управления природными ресурсами.