Гибридная система дифференциальных уравнений, описывающая твердое тело, прикрепленное к двум упругим стержням

Механические системы, состоящие из твердого тела или же системы твердых тел, связанные между собой одним стержнем достаточно подробно исследованы в работе [1]. Уравнения динамики для рассматриваемых систем были получены с применением вариационного принципа Гамильтона — Остроградского, что в свою очередь приводит к возникновению системы дифференциальных уравнений, названных гибридными (ГСДУ). Особенность ГСДУ состоит в том, что она представляет собой систему дифференциальных уравнений, включающая в себя как обыкновенные дифференциальные уравнения, так и уравнения в частных произ- водных. Позже в работе [2] были получены теоретические основы исследования для данного класса гибридных систем, что в свою очередь привело к разработке единого подхода к исследованию собственных колебаний путем построения обобщенных математических моделей применительно к широкому классу механических систем, состоящего из систем твердых тел, закрепленных на балке Эйлера — Бернулли [3].

• 1    Постановка задачи

Механическая система состоит из двух упругих стержней, к которым крепится посредством пружин жесткостью с 1 , с ₂, с ₃, с ₄ твердое тело массой m в точках a 1 , a ₂, a ₃, a ₄ (рис. 1). Зададим 0 xz неподвижную систему координат. Пусть 0 xz имеет начало координат в точке крепления нижнего стержня, а ось 0 x будет направлена вдоль оси этого стержня. Так же нам потребуется подвижная система координат 0 ‘ x'z' , связанная с твердым телом. Будем считать, что в состоянии равновесия оси координат описанных систем параллельны. В рамках заданной механической системы тело с массой m может двигаться поступательно вдоль оси 0 x и одновременно поворачиваться вокруг собственной оси на некоторый угол ф . Функции, выражающие перемещение точек стержней вдоль оси Oz обозначены как u 1 ( x , t ), u ₂ ( x , t ) .

Запишем уравнение перемещения вдоль оси Oz для произвольной точки тела ( x ', z ')

z = z ₀ + z ‘ + x 'ф .                                  (1)

Данное равенство будет справедливо в силу того, что перемещение вдоль оси 0 x отсутствует, а угол ф является достаточно малым.

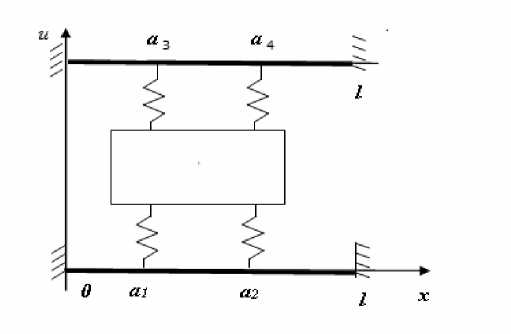
Рис. 1. Механическая система с двумя упругими стержнями

На основании полученного равенства (1), перемещения точек соединения упругих элементов и твердого тела массой m вдоль оси Oz можно описать следующими равенствами zx = z0 + zi'+ d 1Ф, z2 = z0 + z2'+ dФ, z3 = z0 + z3'+ d3Ф, z4 = z0 + z4'+ d4Ф, где z1', z2', z3', z4' — координаты точек соединения тела массы m и упругих элементов вдоль оси Oz, d 1, d2, d3, d4 — расстояния от подвижной оси 0'z' до осей пружин, прикрепленных к стержням в точках

a l , a 2 , a 3 , a 4 .

С учетом полученных выражений (2) запишем потенциальную энергию пружин как квадрат ее линейной деформации.

U = c i ^{( z} 0 ^{+ z} 1 ^-

7             /           2 .      /           '   .    7             /       ,\\ 2

d 1 ф - u 1 ( a 1 , t )) + c ₂ ( z ₀ + z ₂ + d₂ ф - u 1 ( a ₂ , t )) +

/      .    '       7              /      ,\\2         /      .    ' .    7              /       ,\\2

+ c ₃ ( z ₀ + z 1 - d₃ Ф - u ₂ ( a ₃ , t )) + c ₄ ( z ₀ + z 1 + d₄ ф - u ₂ ( a ₄ , t ))

.

Уравнение для кинетической энергии твердого тела массой m будет иметь вид

.2 г • 2

mz_ 1_ф_

T\           ⁺          ,

1     2       2

.

где 1 _ф — момент инерции данного тела относительно центра масс при

повороте на угол ф .

Исходя из технической теории стержней, запишем потенциальную и кинетическую энергии рассматриваемых стержней.

T = ¹ W ( dU ) dx +

2 2 J dt

\pF ( dU ² ) ² dx , dt

U2 =1 fEZ (du )2 dx +

¹      z/2

J El ( d 42 ) ² dx ,

0     dx-

• ²    2 J      dx ²

  
  

где I — момент инерции поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний, E — модуль упругости, F — площадь поперечного сечения и р — плотность материала стержня.

Далее следуя единому подходу исследования свободных колебаний, предложенному для систем, прикрепленных к одному стержню, также воспользуемся вариационным принципом Гамильтона — Остроградского и получим следующий интеграл.

J ( z , p , u₁, u ₂) = J 5 ( T - U ) d1 = 0,                       (6)

где U — кинетическая энергия системы, а T — потенциальная энергия системы.

2 Гибридная система дифференциальных уравнений

Составим вспомогательную функцию с учетом полученных соотношений для кинетической и потенциальной энергии (3)-(5).

р(а) = J(z + aAz,ф + aAp,u + aAu1,u2 + aAи2).

Затем вычислим производную от функции р ( а ) по параметру а и тогда мы сможем определить вариацию функционала действия 5 J при а = 0

5J = 5ф(0) = j^ mz05z0 + 1рф5ф "'dtt - ti

-J[c1( z 0 + z‘ - dp - u1(a1, 1 ))(5z0 - d15p - 5u1(ap1 ))]d1

t i

-J[ c 2( z0 + z 2 + d 2p - u1( a 2,1 ))(5z0 + d 25p - 5u1( a 2,1 ))]d1 - ti

-J[ c3( z0 + z3 - d3p - и 2(a3,1 ))(5z 0 - d35p - 5u 2( a 3,1))]d1 -

• ¹ i

• ¹ 2

• - J [c4 (z0 + z4 + d4ф - и2 (a4,1 ))(5z0 + d45p - 5u2 (a4,1 ))]d1 +

¹ i

l

+J J PF

¹ i _

auiCx,!) d5ui(x,1)   _ l

a 1        a 1         J

du1(x, 1) d25u1(x, 1)

^X    dx2  dx

d1 +

J J PF

¹ i .

du2(x, 1) d5u2(x, 1)

d 1        d 1

, l du^ (x, 1) d25u9 (x, 1) , dx - El —2 \ ---—- dx

0      ax2       ax1

d1.

Далее при помощи вариационного принципа Гамильтона — Остроградского получим t1

8 J = J ( - mz₀ - c₁ [ z 0 + z ’- d ₁ ф - u₁ ( a 1 ,t ) ]- c 2 [ z 0 + z 2 + d 2 ф - u₁ ( a 2 , t ) ] + t ₀

+c3 [z0 + z3 - d3ф-u2 (a3,t)]-c4 [z0 + z4 - d4ф -u2 (a4,t)])8z0dt + t1

+J(- 1фФ + c1 d 1 [ z0 + z1 - d 1ф - u1 (a1, t)] + c 2 d 2 [ z 0 + z 2 + d 2ф - u1 (a 2, t)] + t0

t ₁

⁺ J ( ^{- 1} ф ^{Ф + c} 1 ^d 1 [ ^z о ⁺ z ^{2 - d} 1 Ф ^{- u} 1 ( ^a 1 , t ) ] ^{+ c} 2 ^d 2 [ ^z о ^{+ z 2 + d} 2 Ф ^{- u} 1 ( a 2 , t ) ] ⁺ t ₀

+c3d3 [z0 + z3 -d3ф-u2 (a3,t)] + c4d4 [z0 + z4 + d4ф -u2 (a4,t)])8фdt + t1l

+JJ(c [z0 + z‘ - d 1ф - uj (x,t)] + c2 [z0 + z2 + d2ф - ut (x,t)]- t00

d u       'u u i |e

• - pF —-— EI —— 8 u dxdt +

d t ²          d x ⁴ J ¹

t 1 l

+ JJ ( c 3 [ z 0 + z 3 - d₃ ф - u 2 ( x , t ) ] + c ₄ [ z 0 + z 4 + d₄ ф - u 2 ( x , t ) ] t 0 0

—

• p F^{( u}2 - ei ^{d u}2 1 8 u,dxdt = 0.

dt ²        ax⁴ J ²

Далее согласно основной лемме вариационного исчисления мы получим ГСДУ для динамики системы. Так как допустимые вариации 8 z ₀( t ), 8ф и 8 u₁(x , t ), 8 u ₂( x , t ) независимы и произвольны.

mz ₀ + c ₁ [ z ₀ + z ‘ - d_x ф - u ₁ ( a ₁, t ) ] + c ₂ [ z ₀ + z '₂ + d ₂ ф - u ₁ ( a ₂, t ) ] +

+ c ₃ [ z ₀ + z 3 - d 3 Ф - u ₂ ( a ₃, t ) ] + c ₄ [ z ₀ + z 4 + d ₄ ф - u ₂ ( a ₄, t ) ] = 0;

• ¹ ф ^{ф -} c 1 ^d 1 [ z 0 ⁺ z ^{2 - d} 1 Ф ^- u 1 ( a 1 , t ) ] ⁺ c 2 ^d 2 [ z 0 ⁺ z ^{2 + d}2 Ф ^- u 1 ( a 2 , t ) ] ⁺

• - c ₃ d ₃[ z ₀ + z 3 - d 3 Ф - u ₂ ( a ₃, t ) ] + c ₄ d ₄ [ z ₀ + z 4 + d₄ ф - u ₂ ( a ₄, t ) ] = 0;

p F ^ u ^{1 + EI д}Г 4Г = ^c 1 [ ^z 0 ⁺ z ^{2 - d} 1 Ф ^{- u} 1 ( ^x , t ) ] ⁸ ( ^{x - a} 1 ) ^{+            (7)}

d t       dx

+ c ₂ [ z ₀ + z 2 + d₂ ф - u ₁ ( x , t ) ] 8 ( x - a ₂ )

p F ^d ur ^{+ EI} ^I x r = ^c 3 [ ^z 0 ^{+ z} 3 ^{- d} 3 Ф ^{- u} 2 ( ^x , t ) ] ⁸ ( ^{x - a} 3 ) ⁺

+ c ₄ [ z ₀ + z 4 + d₄ ф - u ₂ ( x , t ) ] 8 ( x - a ₄ ) .

Систему (7) приведем к следующему виду

Zo + Pi2 (zо + z‘-d1Ф -U\ (a\,t)) + P22 (zо + z2 + d2Ф - u (a2,t)) + +p32 (z0 + z3- d3p-u2(a3,t)) + p42(z0 + z4 + d4p-u2(a4,t)) = 0, ф - q12 (z0 + z‘ - d 1p - u 1 (a1, t)) + q22 (z0 + z2 + d2p - u1 (a2, t ))--q32 (z0 + z3 - d3p - u2 (a3,t)) + q42 (z0 + z4 + d4p - u2 (a4,t)) = 0, d2 ui dt2

, d4u, +b dt4

= e1 (z0 + z‘ - d 1p - u 1 (a1, t)) 5 (x - a1) +

+e2 (z0 + z‘ + d2p - u 1 (a2, t)) 5 (x - a2)

d ² и 2 dt t

, d4u2 + b —t dt4

= e3 (z0 + z‘ - d3p - u2 (a3,t))5(x - a3) +

+e4 (z0 + z4 + d4p - u2 (a4,t))5(x - a4), c cd EJ c где p, = J -, q, =.     , b = ™77, e =    , 1=1,..4.

V m у I _p    p F     p F

На u 1 ( x , t ) , u ₂ ( x , t ) , наложены граничные условия:

u 1 ( 0, t ) = u 1 ( l , t ) = 0, u ₂ ( 0, t ) = u ₂ ( l , t ) = 0,

^Ц ¹ ( 0, t ) =d u > ( 1 , t ) = 0,    d u ² ( 0, t ^d u ² ( 1 , t ) = 0

dx       dx           dx       dx

3 Дифференциально-алгебраическая система дифференциальных уравнений

Подставим в (8) z ₀, p , u 1 ( x , t ), u ₂( x , t ) в следующем виде:

z 0 = A s1n(®t),                 p = Аф s1n(®t), u1 (x, t) = V1 (x) sin (rot),          u2 (x, t) = V, (x) sin (rot), и из системы (8) получим дифференциально-алгебраическую систему уравнений.

-to ² A + ^p 2 ( A + z ’ ^- d ] A , ^- V 1⁽ a )) + p 2 ( A + z\ + d 2 A , ^- V ⁽ a 2 )) + + p 2 ( A + z 3 - d 3 A , - V 2 ( a 3 )) + p 4 ( A + z ‘ + d 4 A , - V 2 ( a 4 )) = 0,

• - to ² A , - q 1 ( A + z ‘ - d 1 A , - V ( a i )) + q 2 ( A + z 2 + d 2 A , - V ( a 2 ))

  _-

  
  
  
  

• - q 3 ² ( A + z 3 - d 3 A , - V _z ( a 3 )) + q 4 ( A + z 4 + d 4 A , - V 2 ( a 4 )) = 0,

d V M

• - to ² V ( x ) + b ---= e, ( A + z ‘ - dA - V ( x )) 5 ( x - a_x ) +

• ¹                    dx ^{4            1            1         1             1                       1}

+ e ₂ ( A + z ‘ + d ₂ A , - V₁ ( x )) 5 ( x - a ₂)

₇         d ⁴ V₇(x)

-to ² V ( x ) + b ---.   = e ( A + z ‘ - dA - V ( x )) 5 ( x - a ₃) +

• ²              dx ^{4        3        3     3         2                3}

+ e ₄ ( A + z 4 + d ₄ A , - V ₂ ( x )) 5 ( x - a ₄).

В силу того, что соотношения три и четыре из (10) понимаются в обобщенном смысле, то для произвольной основной функции ,(x, t) бу дут справедливы следующие равенства:

г 7 d ⁴ V ( x ) , _х

J ( - to 2 V ( x ) + b -----4 ) , ( x , t ) dx =

^J₀         ¹              dx ^{4       3}    '

= C1(A + z’ - d 1 A, -V1(aj),(a1,t) + e2(A + z2 + d2A, - V^(a2)),(a2,t), г 7            d4 V, (x) z x

J ( - to ² V ( x ) + b ----5^) , ( x , t ) dx =

^J₀        ²             dx ^{4       3} '

= e ₃( A + z 3 - d ₃ A , - V ₂( a ₃)) , ( a ₃, t ) + e ₄( A + z 4 + d ₄ A , - V ₂( a ₄)) , ( a ₄, t ) .

А полученные условия для функций V ( x ) , V ₂ ( x ) из граничных условий (10) будут иметь следующий вид:

V (0) = V (1 ) = 0,     v2 (0 ) = V2 (1 ) = 0,

dV- (0) = dV- (I ) = 0,    dV^ (0 ) = dV^ (l ) = 0.

dx dx           dx dx

Теорема 1 . Пусть G₁ ( x ) , G ₂ ( x ) , G ₃ ( x ) , G ₄ ( x ) — обобщенные решения уравнений

-to2Gi(x) + b^ ^4(x) = 5(x), i = 1,..4.

Тогда для любых to , A , A , решения системы

-to V (x) + b —-^-4—- = e1 (A + z1 - d 1 A, - V (x)) • 5 (x - a1) +

+e 2 (A + z ‘ + d 2 A, - V (x)) • 5 (x - a 2)

2 , х    d4V (x)

—to2 V (x) + b---= e

^2V           dx^{4       3}

—

d 3 A v

—

x — a з) +

+e4 (A + z 4+ d4 Av — V2 (x)) • 5(x — a 4)

будут иметь вид

V1 (x ) = G1 (x — a1 )• e1( A + z; — d 1 Av — V1( a1))+

+ G 2 ( x — a 2 ) • e 2 ( A + z ‘ + d 2 A v — V ( a 2 ))

V2 (x) = G3 (x — a3 )• e3 (A + z3 — d3AV — V2 (a3 )) +

+ G4 (x — a 4) • e4 (A + z 4 + d4 Av — V2 (a 4))

и удовлетворять следующим краевым условиям

G , ( ■ a, ) = G , (l — a , ) = 0, dG ( ■ a , ) = dG ( l — a , ) = 0. dx        dx

Доказательство.

Запишем уравнение один из системы (16) в следующем виде: l

V (x) = J G1 (x — 5) e (A + z; — d1 Av — V (5 ))5(5 — a1) d? + 0

l

+J G, (x—5) e2 (A + z 2+ d 2 Av — V(5))5(5 — a 2) d5.

Подставим получившееся V ( x ) в левую часть уравнения (11).

Затем

умножим на v ( x , t ) и проинтегрируем по переменной x от 0 до l с заменой порядка интегрирования. Тогда с учетом (14), мы получим:

ll

, d⁴G ( x — 5 ), b —’ ₄   ) *

0 0

* e ( A + z \ —

dx

d 1 Av — V1 (5)) 5 (5 — a1) +

/ 2^/        dd4g2(x — 5),

+(—to G2 (x — 5) + b----------) *

dx

* e 2 (A + z \ + d 2 Av — V (5)) 5(5 — a 2)] d5v( x, t) dx =

l

= J[ei (A + zi - di A, - Vi (5)) 5 (5 - ai )* 0

(L 2^z LdG(x-^ч.^

* J ( - ® ² G ( x - ^ ) + b ----¹—4----) , ( x , t ) dx +

I0                      dx4

⁺ e 2 ( A ⁺ z 2 ^{+ d} 2 ^А ф - ^{V (} ^ ) ) ⁵⁽^ - a 2 ) *

* [( - ® ² G ₂( x - ^ ) + b     ²( x ——) , ( x , t ) dx ] d e =

I0                        dx4

zz

= J[ei (A + z’ - d 1 A, - V, (5))5 (^ - ai )J,(x, t)5 (x - ^)dx + 00

I

+ e2 (A + z\ + d2A, - V (^))5(^ - a2) J,(x,t)5(x - ^)dx]de =

= e i ( A + z ’ - d i A , - V i ( a i ) ) , ( a i , t ) + e 2 ( A + z 2 + d 2 A , - V ( a 2 , t ) ) , ( a 2 ), что соответствует правой части первого соотношения из (ii). Доказательство второго соотношения из (i6) для функции V , ( x ) получается аналогично. Что и требовалось доказать.

Заключение

В данной работе была рассмотрена возможность применения единого подхода исследования свободных колебаний, ранее предложенного при исследовании систем, состоящих из твердых тел, прикрепленных к одному стержню, применительно к малоизученным системам твердых тел, прикрепленных к двум стрежням. Для этого была построена математическая модель, которая в свою очередь так же имеет вид ГСДУ вследствие использования вариационного принципа Гамильтона — Остроградского. Также была сформулирована и доказана теорема о представлении решений вспомогательной дифференциально-алгебраической системы уравнений, на основе которой в дальнейшем строится уравнение частот, аналогично [2, 4]. В дальнейшем планируется обобщение полученных ранее результатов для систем твердых тел, закрепленных на двух и более стержнях. Подобные модели широко используются в машиностроении и аэродинамике. Например, они могут найти применение в области исследования систем виброзащиты объектов.