Гибридные модели в задачах экономической динамики

В современных исследованиях по математической экономике все более ощущается потребность в более совершенных математических моделях. Это было предсказано В. Леонтьевым еще в 1953 г. [12, c.101]: «Некоторые из структурных отставаний (лагов), встречающихся в текущих описаниях эмпирических взаимоотношений между затратами производства и выпуском продукции, включают, например, наличие причинности, действующей в промежутке времени – некоторого мистического взаимоотношения, которое при более тонком и детальном рассмотрении может свестись к интуитивно более удовлетворительной и математически более удобной дифференциальной формулировке».

Наиболее популярным в теоретических и прикладных исследованиях является класс моделей динамики с дискретным временем и постоянными параметрами (коэффициентами). В линейном случае такая модель имеет вид системы разностных уравнений:

z ( 0 = T j ⁽ t j ) + Y F k u(t k ) + f(t i ), i = ^0,1,---, м , ⁽¹⁾ j =1 k =1

где 0 = t₀< t_x<...< t ^ = T , векторная переменная z = col( z_t ,..., z_n) (набор эндогенных переменных) описывает состояние моделируемой системы в моменты времени t ; u = col( u ,..., u_r ) - набор экзогенных (в том числе управляющих) переменных, предыстория всех переменных считается заданной:

^z( ^ ) = Ф^, ^u(. & = ¥ ⁽ ^ ) , если ^ < ⁰ .

Основная причина наибольшей распространенности моделей (1) – детально разработанная теория идентификации таких моделей — эконометрика. В рамках эконометрического подхода получены ответы на многие вопросы, имеющие прямое отношение к обоснованию и оценке возможностей практического применения моделей векторной авторегрессии (VAR) [см., напр.:28], разработаны методы построения оптимальных точечных и интервальных оценок параметров (элементов матриц B_} , F_k ) системы

(1), процедуры проверки гипотез о значимости этих параметров и требования к исходным данным, которые используются для идентификации модели. Принципиальный момент здесь — гипотеза о постоянстве параметров модели. Модели вида (1) составляют основу инструментария информационно-аналитических систем (ИАС), разрабатываемых компанией «Прогноз» (г. Пермь) [3, с.60-164; 6].

Вопросы построения моделей с дискретным временем и переменными коэффициентами рассматриваются в рамках теории протомоделей, построенной В.Д. Фурасовым [21]. При этом из множества моделей, совместимых с наблюдаемыми вход-выходными последовательностями, выделяются подмножества моделей, обладающие специальными свойствами, и синтезируются уравнения протомоделей, порождающих соответствующие подмножества моделей исследуемой системы. Эти модели используются, в частности, для исследования так называемых индексов развития динамических процессов и корректной формализации понятий спада и подъема.

Задача построения моделей с непрерывным временем при условии непрерывных наблюдений может решаться на основе идеи операторной интерполяции, высказанной Н.В. Азбелевым в 1988 г. Таким задачам в рамках функционально-дифференциальных моделей с последействием посвящен цикл работ С.Ю. Култышева и Л.М. Култышевой [9, 10, 11]. Отметим также новый подход к построению дифференциальных уравнений произвольных динамических процессов, предлагаемый в работе [19].

Оставляя в стороне вопросы обоснования выбора и построения упомянутых моделей, мы сосредоточимся на проблеме синтеза моделей с дискретным временем и функциональнодифференциальных моделей с непрерывным временем. Один из основных аспектов этой проблемы — возможность использовать в полной мере отдельно полученные к настоящему времени теоретические результаты для функционально-дифференциальных моделей [1, 2, 27] и для моделей в форме разностных уравнений [4, 5, 24]. Термин «гибридные» по отношению к системам уравнений и моделям используется достаточно широко и нередко в различных смыслах [см., напр.: 22, 23, 15, 16, 17]. В нашем случае он кажется вполне уместным. Напомним, что «гибрид» (от лат. hibrida - помесь) — организм, полученный в результате скрещивания генетически различающихся родительских форм (видов, линий и др.)» [20]. Вопрос о существенности генетических различий разностных уравнений и уравнений дифференциальных (и их обобщений) имеет философский подтекст. Приведем в связи с этим высказывание А.Н. Колмо- горова: «Весьма вероятно, что с развитием современной вычислительной техники будет понятно, что в очень многих случаях разумно изучение реальных явлений вести, избегая промежуточный этап их стилизации в духе представлений математики бесконечного и непрерывного, переходя прямо к дискретным моделям» [8, с.28].

Динамические модели, рассматриваемые в этой работе, с одной стороны, представляют собой конкретную реализацию абстрактных функционально-дифференциальных уравнений. С другой стороны, они охватывают широкий класс моделей, возникающих при исследовании реальных экономических и эколого -экономических процессов с учетом эффектов последействия (запаздывания) и импульсных возмущений (шоков), приводящих к скачкообразному изменению основных показателей функционирования изучаемой системы. Рассматриваемые модели содержат одновременно как уравнения, описывающие динамику показателей в непрерывном времени на конечном промежутке, так и уравнения с дискретным временем, характерным для эконометрических моделей. Для указанного класса систем исследуется вопрос о представлении решений, ставятся краевые задачи о достижимости заданных значений показателей, задачи управления и приводятся условия неразрешимости этих задач в форме, допускающей эффективное исследование с использованием современных компьютерных технологий.

1. Предварительные сведения. Функционально-дифференциальные уравнения с импульсным воздействием

Приведем здесь необходимые для дальнейшего сведения из [1, 2, 26, 27].

Обозначим через   L n = L n [0, T ]   пространство      суммируемых      функций

T

v:[0,T] ^Rn  с нормой PvP= j| v(s)|лds , где | • |и — норма в Rn (далее, если размерность пространства очевидна, индекс у нормы будем опускать).

Зафиксируем отрезок [0,T] с R и ко- нечное           множество           точек

{ т ₁ ,...,Т т }, 0< Т 1 <...< т _т < T и, следуя А.В.

Анохину [7], введем пространство DSⁿ ( m ) кусочно абсолютно непрерывных функций y : [0, T ] ^ Rⁿ , представимых в виде

y ⁽ t ⁾⁼J n v ⁽ s ) ds + y ⁽⁰⁾ +2 Л n

^{J 0}                 tT^{[ T} k , T ^]

⁽ t ^{) A} y^{( T} k ), (2)

где      v e L n ,      A y ^{( T} k ) = y⁽ T ) ^- y^{( T} k ^{- 0)} ,

X ту (t) — характеристическая функция от резка [Tk ,Т ].

Элементы пространства DS n ( m ) — это функции, абсолютно непрерывные на каждом из промежутков [0, т ), [ TT ),..., [ t T ] и непрерывные справа в точках T ,..., Т_т .

Если норма в DSn (m) определяется равенством m

P У P DS n ( m ) =P У P _Ln + I У (0)1 n + Z I ^A У T )l n , k =1

то DSⁿ ( m ) — банахово пространство.

Сделаем несколько замечаний об изучении импульсных систем с использованием пространства DSⁿ ( m ) . Подход к изучению дифференциальных уравнений с разрывными решениями связан с теорией так называемых «обобщенных дифференциальных уравнений», предложенной J. Kurzweil [29]. К настоящему времени эта теория хорошо разработана [см., напр.: 32, 25]. Согласно принятому подходу импульсные уравнения рассматриваются в классе функций ограниченной вариации. В этом случае под решением понимается функция ограниченной вариации, удовлетворяющая интегральному уравнению с интегралом Лебега-Стильтьеса или Перрона-Стильтьеса. Интегральные уравнения в пространствах функций ограниченной вариации представляют интерес сами по себе и детально изучаются [см. 33]. Напомним, что функция ограниченной вариации представима в виде суммы абсолютно непрерывной функции, разрывной функции и сингулярной компоненты (непрерывной функции с производной, равной нулю почти всюду). Решения уравнений со скачками, рассматриваемые ниже, не содержат сингулярной компоненты и могут терпеть разрывы только в конечном числе заданных точек. Эти уравнения рассматриваются в пространстве DSⁿ ( m ) - конечномерном расширении традиционного пространства абсолютно непрерывных функций. Такой подход к уравнениям со скачками был предложен в [7]. Он не использует сложную теорию обобщенных функций и находит много приложений в тех случаях, когда вопрос о сингулярной компоненте не возникает.

Рассмотрим в пространстве DSⁿ ( m ) уравнение [14]:

y ( t ) = f t K '( t , s ) y ( s ) ds + A 0 ( t ) y (0) + w 0

m                                           (3)

+ X A k ( t ) A У( T k ) + f ( t ), t e [0, T ].

k =1

Здесь элементы k 0 ( t , s ) ядра K 1 (t , s ) измеримы на множестве {( t , s ):0„ s „ t „ T } и имеют общую, суммируемую на [0, T ] , мажоранту:

I k ij (t , s )|„ K ( t ) i , j = 1,..., n, t e [0, T ], а ( n x n ) -матрицы A 1 ,..., A ° имеют суммируемые на [0, T ] элементы. Уравнение (3) охватывает дифференциальные уравнения с сосредоточенным или распределенным запаздыванием и интегродифференциальные системы Вольтерра.

Напомним [1, 2], что пространство

DSⁿ ( m ) изоморфно прямому произведению L x R^{n + mn} ,     изоморфизм       J = { Л , 0 }:

L x R^{n + mn} ^ DSⁿ ( m ) задается равенствами

t

(Лу)(t ) = Jv (s) ds;  (0в)( t ) = 0( t )в, где        0(t) = [En,En • xpT](‘)’-’En ’ Xm,T](‘)) , в e Rn+mn, e - единичная (n x n) -матрица. Обратный                         оператор

J ^{- 1} = [ ^ , r ]: DSⁿ ( m) ^ L x R n ^{+ mn} определяется равенствами

$ У = ^У ;   ГУ = col⁽ У ⁽⁰⁾, ^А У ^{( т} 1 ), • • •, ^А У ^{( T} m )).

Тогда

У = Л^у + 0 гу.                 (4)

Уравнение (3) является частным случаем линейного абстрактного функциональнодифференциального уравнения (АФДУ)

L У = ^ ,                           (5)

где L : DSⁿ ( m ) ^ L - линейный ограниченный оператор. Применяя оператор L к обеим частям равенства (4), получим

L у = ( L Л ) ^ у + ( L 0 ) гу = Q S y + Ary = f . (6) Оператор Q = L Л : L ^ L называют главной частью оператора L , а A = L 0 : R^{n + mn} ^ L — конечномерной частью оператора L . В уравнении (3) оператор Q является вольтерро-вым:

t

(Qv)(t) = У(t) - J к1 (t,s)V(s)ds и обратимым. Обратный оператор Q-1 имеет представление

t

(Q-1 f)(‘ ) = f (‘) + J R (t, s) f (s) ds, где R(t,s) - резольвентное ядро, соответствующее ядру K1 (t,s) . Оператор A в (6) для уравнения     (3)     задается     матрицей

a=(-4, - a;,..., - a1) .

Получим представление решения уравнения (3). Применим Q ^{- 1} к обеим частям последнего равенства в выражении (6):

и проинтегрируем полученное равенство от 0 до t :

ttt

j ^{( S} y ⁾⁽ s ) ds = f ^{( Q _|} f ⁾⁽ s ) ds - [ ^{( Q} a ⁾⁽ s ) ds • ry .

0                    00

Так как

j (Sy)(s) ds = ESy = y -0 ry то

y ( t ) = I 0 ( t ) - j ( Q-¹ A )( s ) ds I ry + j ( Q-¹ f X s ) ds =

I       0             J 0

= ( 0 ( t ) + X ( t ) ) ry + j ( Q ^{- 1} f )( s ) ds .

В самом деле, t      tts

J ^C i ⁽ t , ^s ) ^{f ( s} ) ^ds = j ( ^{Q - 1 f} ) ^{( s} ) ^ds = j j ^{f ( s} ) ⁺ j R ^{( s , r ) f ( t ) d r} I ^ds =

0                          0                         0 I           0

= j f ( s ) ds + j J r ( s , r ) ds f ( r ) d r = j ^J E „ + J r ( t , s ) d r I f ( s ) ds.

0                0 r                                0 L        sJ

Общее решение уравнения (3) имеет вид t y (t ) = Y (t )a + j C|( t, s) f (s) ds, n+mn где a g R     - произвольный вектор. Это представление позволяет свести исследование краевых задач и задач управления к исследованию систем линейных алгебраических уравнений.

Рассмотрим общую линейную краевую задачу для уравнения (3): t

^{y (} t ) = j ^{K 1 (} t ’ s ) ^{y (} s ) ds ⁺ A ⁽ t ) y ^{(0) +}

Каждый столбец x (t) (n x (n + mn)) - матрицы

X (t) = -j (Q - A )(s) ds = - jJ A( s) + j^ (s,t)A(r) dr I ds 0                          0 I           0                      J является решением задачи Коши

x ( t ) = j K ^;( t , s ) x ( s ) ds - a_t ( t ),

x (0) = 0, t g [0,7 ], где a. (t) - i -й столбец матрицы A .

Однородное      уравнение      (3)

( f ( t ) = 0, t g [0, 7 ]) в силу представления (7)

имеет фундаментальную матрицу Y ( t ) размерности n x ( n + mn ) :

Y (t ) = 0 ( t ) + X (t ).

Решение уравнения (3) с начальными условиями

y ⁽⁰⁾ = 0, A y ^{( T} 1 ) = 0,..., A y ^{( r} m ) = ⁰

имеет представление tt y (t) = J (Q4 f) (s) ds = (C| f) (t) = J C|( t, s ) f (s ) ds, 0                                         0

где C (t,s) — матрица Коши [12, 13]. Эта мат рица является решением матричного уравнения

C 1 ( t , s )=f K ^;( t , t )^ C ; ( t , s ) d T + K '( t , s ),  0„ s „ t „ 7

dt          *        dr с условием C (s,s) = En .

Матрица Q ( t , s ) выражается через резольвентное ядро R ( t , s ) :

t

Q ( t , s ) = E_n + j R ( r , s ) d r .

s

m

+£A‘(t>Ay(rk ) + f (t), t g [0,7], k=1

£y = Y, где I:DSn (m) ^ Rn+mn — линейный ограниченный вектор-функционал. Всякий такой вектор-функционал имеет представление

T

m

£y = j ^{ф (} s ) ^{y (} s ) ds + T 0 • y ⁽⁰⁾ + ^ k •^A y( r ).

0                                        k =1

Здесь    элементы     ((n + mn) x n) - матрицы Ф измеримы и ограничены в суще ственном,    То,..., Ym    — постоянные

(( n + mn ) x n ) -матрицы.

Применяя вектор-функционал к обеим частям (9), получим систему линейных алгебраических уравнений относительно вектора a :

£y = (Ya + £< j C ( • , s ) f ( s ) ds I = Y .

L о                    J

Таким образом, необходимое и достаточное условие однозначной разрешимости краевой задачи (3), (9) имеет вид:

det/ Y * 0.

Рассмотрим задачу управления y (t ) = jK1( t, s ) y (s ) ds + A0(t) y (0) + |jAk( t )• Ay (rk ) +

+ ( F u ) ( t ) + f ( t ), t g [0, 7 ]

y (0) = a 0 ,  fy = Y G R N .

В уравнении (11) F : Lr [0,7] ^ L [0,7] - ли- нейный ограниченный оператор,  Lr  – про- странство функций u : [0,T] ^ Rr, суммируемых с квадратом, с нормой ЦиЦ^ =  ,

T где < u, v >= f uT(s)v(s)ds , -T - знак транспо-0

нирования.

Запишем решение уравнения (11), ис пользуя формулу (9):

y ( t ) = Y ( t ) • col( a , c ) + f C ( t , s ) f (s ) ds +

+ JC (t, s) (F u) (s) ds, где ст = col (Ay (t ),•••, Ay (rm ) ) . Применим последнему равенству вектор-функционал :

к

Будем искать управление u в виде ли- N нейной комбинации u = [ F *V ]^T( s ) d = Z dW , i =1

где   w_t  — i -й столбец матрицы [ F * V ]^T .

Напомним, что в силу теоремы об ортогональном разложении гильбертово пространство L^r можно представить как прямую сумму:

L2= Sp (V|,-, Vn ) Ф Sp (V|,..., Vn )1, где Sp(v,...,vN) - линейная оболочка элементов (V|,...,Vn), а Sp(V|,...,Vn)1 — ее ортогональное дополнение. Запишем (13) как систему линейных алгебраических уравнений относительно   (mn + N)  — вектора  col(c, d), с e Rmn, d e RN :

t y = t {Y ( • ) } col( a , c ) + Ш с ( • , s ) f ( s ) ds k +

10                     J

[52 + (Y,,..., Ym) ]c + Md =

+ « J C ( • , s ) ( F u ) ( s ) ds > .

10                             J

Для первого слагаемого имеем:

Г T                    m                  1

({ Y (•) } col( « 0 , c ) = 1 f ф( r ) Y ( r ) dr + T 0 Y (0) + Z' P k [ Y ( r k ) - Y ( r k -0)] kx

T

= Y ^- f ^{V (} s ) ^{f (} s ) ds ^- ( ⁵ | + ^T 0 ) ^a 0 ,

где ( N x N ) -матрица M определена равен-

m xco1 {«0 с} = 5| • «0 + 52 ■Ay + T0a0 +Z k=|

где ( N x ( n + mn )) -матрица

T

5 = f ^{ф (} т ^{) Y T )} d r = ( H | , H ₂ ) , 0

матрица, состоящая из первых

₄ — ( N x n ) -

n столбцов мат-

рицы 5 , для второго слагаемого имеем:

I1T       Г т д1

£ 1 f C |G s ) f ⁽ s ) ds k = f ^{Ф Т )} 1 f — C ( r , s ) ^f ( s ) ds + f ^T ) k d r =

10                  J 0        10 dTJ

= f Ф(s) f (s)ds + ff Ф(т) ^ C(r,s)dr • f (s)ds = fV(s) f (s)ds, 0                   0s       dr0

T где V (s) = Ф( s) + f Ф(г) • — C (r, s) dr.

Js

Таким образом,

T

T

= r - f V ^{( s} ) f ( ^s ) ^{ds -} ( ⁵ 1 +^ 0 ) « 0 - 0

T

Запишем f V ( s )( F u )( s ) ds в виде о

T f (F V)(s) • u(s)ds,

*

L 1^1 L )  — сопряженный к F оператор.

T ством M = f [F *V] (s) •[F *V]T(s)ds. 0

Тогда разрешимость задачи управления (11) – (12) равносильна разрешимости системы (14) относительно вектора col( c , d ) . Каждое

решение   col( c ₀, d ₀) ,     c ₀ = col( c ^|,..., c m ),

системы (14) определяет решение задачи (11) –

(12),        включающее

N u = Zd0 W u e L, i=|

A y ( r k ) = & 0 , k = |,--, m .

и

управление скачки

2. Предварительные сведения. Модели с дискретным временем

Зафиксируем             множество

J = { t 0 , t | ,..., t . },  0< t |<...< t . = T . Через

FD ^v ( p )  обозначим пространство функций

z : J ^ R ^v с нормой:

p

P z P F ., , , " Z z ( t i i =0

Рассмотрим в пространстве FD ^v ( p )

уравнение

i - |

z ⁽ t i )= Z B j z ⁽ t j ) ⁺ g ⁽ t )’   i =^1,—, p ,   ⁽¹⁵⁾

j =0

где Б, 2 — постоянные ( v x v ) -матрицы.

Для разностного уравнения (15) можно записать разностные аналоги определений, задач и утверждений п.1. [см.: 4].

Фундаментальная матрица однородного уравнения (15) ( g ( t ) = 0, i = 0,..., д ) является решением начальной задачи i - i

Z ( t .) = ^ B j Z ( t j ),  i = 1,..., Д ,   Z (t o ) = E v .

j =0

Матрица Коши C2 (i, j) определяется рекуррентными соотношениями i-1

C2(i,j) = Ev + EBCi(k,j),  1 „ j„ i„ Д, k=j и дает представление решения уравнения (11) при условии z(tQ ) = 0 :

i

z ⁽ t i) = ^{( C} 2 g ⁾⁽ t ) = E C 2 ^{( i} , j ) g ⁽ t j ), j = ¹> —, Д     ⁽¹⁶⁾

j =1

Как обычно, здесь и далее будем считать, что l

E Fi = 0 для любых F , если l <  k . i = k

Таким образом, общее решение уравнения (15) имеет вид

z ( t i ) = Z ( t i ) e + ( C ( g ) ( t i ),   i = 0,..., Д ,   (17)

где β ∈ R ^ν – произвольный вектор.

Представление (17), как и его аналог для функционально-дифференциального уравнения (9), позволяет свести вопрос о разрешимости краевой задачи и задачи управления к исследованию систем линейных алгебраических уравнений.

Рассмотрим общую линейную краевую задачу для уравнения (15):

i - 1

z(ti)=EBiz(ti)+g(ti),  i=1’-,д, j=0

Az = Y, где A:FDv ( д) ^ RA — линейный ограниченный вектор-функционал. Всякий такой вектор-функционал имеет представление:

µ

Az = £Г kz (tk ), k=0

где Г, k = 0,1,..., Д — постоянные (v x v) - матрицы.

Применяя вектор-функционал λ к обеим частям равенства (17), получаем систему линейных алгебраических уравнений относительно вектора β :

µµ

A z = E ^r k Z ( t k ) в + E r k ( C i g ) ( t k ) = Y k =0                 k =0

и критерий её однозначной разрешимости ∀ β ∈ R ^ν :

µ det ErkZ(tk) ^ 0.

k =0

Рассмотрим задачу управления

z ⁽ ti )= E B j z ^{( t} j ) ⁺ ( ^Fu )ft) ⁺ g ⁽ t) ⁱ =¹’-, д  ⁽¹⁹⁾

j =0

z (t_Q ) = a , A z = y ^e R N ,        (20)

где линейный ограниченный оператор F : FD ^v ( д ) ^ FD ^v ( д ) имеет представление:

( Fu ) ( t ) = E Bu ( t k ),   i = 1,-, Д .

k =1

Все решения задачи Коши (задачи (19) с начальным условием z ( t ₀) = a ) имеют вид:

z (t i ) = Z (t i ) a + ( C i g ) ( t i ) + ( C 2 Fu ) ( t i ).

Применяя к последнему равенству вектор-функционал λ , получаем

Все управления, решающие задачу Коши, — это решения системы где в = Y — AZ a — ACg, относительно u : µi                 j

A C i Fu = ET-E C i ( i , j ) ■ E^Fu ( t k ) = H • U = в , i =1     j =1               k =1

где H - матрица размерности ( N x рд ) , U = col ( u ( t_{ ),..., u(t )) - вектор размерности

ρµ , β ∈ R^N .

Будем искать управление в виде N

U = H ^T d = E ( H ^T)i ■ di , i =1

где ( H ^T ) - i -й столбец матрицы H ^T .

Тогда критерий разрешимости задачи управления (19)–(20) имеет вид:

det( HH ^T) ^ 0.

3. Гибридные модели

Мы рассмотрели уравнение (3), описывающее динамику показателей, входящих в y ( t ) , в непрерывном времени на конечном промежутке, и уравнение с дискретным временем (15), характерное для эконометрических моделей. Запишем уравнения (3) и (15) в операторной форме:

У = T11У + f z = T 22z + g где T j : DSn (m) 4 Ln; и

T ₂₂ : FD ^V ( a ) 4 FD ^V ( a ) - линейные ограниченные операторы:

(T _H y )( t ) = f K ¹( t , s ) y ( s ) ds + 4( t ) y (0) +

J 0

m                                            ( T 11 )

+ XAk(t)AyT), t e [0,T], k=1

но вектора x = col ( y , z ) . Для этого воспользуемся следующей леммой.

Лемма. Пусть Aj и A₂ в определении операторов T и T таковы, что

A+a2* 0.

Тогда оператор

( T 22 z )( t i ) = £ B^ ( t j ) i = 1,..., A -    ( T 22 )

j =0

Введем связывающие операторы

T ,₂: FD ^V ( a ) 4 L " и   T ₂₁ : DS" ( m ) 4 FD ^v ( a ) :

(T12z)(t)=    £   Bj(t)z(tj),t e[0,T], (T12), j\.} где элементы матриц B*,j = 0,,...,a, суммиру

р =

Г I к—C2 T 21

- C T J

^{1 12} | : DS" ( m ) х FD ^V ( a ) 4

4 DS” ( m ) х FD ^V ( a )

обратим.

Доказательство. Легко проверить, что

линейный оператор M =

с линейными

емы        на          [0, T ] ,          A >  0 ;

( T 21 y )( t i ) = r i Kf( S ) y ( S ) ds + A 0 y (0) +

J 0

m                                      ^{( T} 21 )

+ £ A ik ^A y ^{( T} k ), ⁱ = ^0,i,..-, A , k =1

где элементы матриц K² измеримы и ограничены в существенном на [0, T ] и A_l ² 2 - постоянные       ( v х n ) -матрицы,       i = 0,1,..., a ,

операторами A : Z 4 Y и B : Y 4 Z ( Y и Z -банаховы пространства) обратим, если оператор ( I — BA) : Z 4 Z имеет обратный оператор

(I — BA) 1 : Z 4 Z . При этом также существуют обратные операторы (I — AB)—1 и м-1 J (I — AB)—1   —(I — AB)-1A "

A B ( I — AB ) ^{— 1}    ( I — BA ) ^{— 1} _J ’

k = 0,1,..., m , A₂> 0 .

Рассмотрим систему, включающую од-

новременно уравнения обоих типов: y = T11 y + T12 z + f’ z = T 21 у + T 22 z + g.

Систему (21) естественно назвать «гибридной» системой или системой непрерывно-дискретных функционально-дифференциальных уравнений.

Применим представления (9) и (17) к первому и второму уравнениям системы (21) соответственно:

В      условиях      леммы      оператор

BA = CT21C1T12 : FDV (a) 4 FDV (a) является t -вольтерровым [13,  c.106] оператором с t = A + A2 и, следовательно, нильпотентным оператором. Таким образом, спектральный радиус оператора BA равен нулю.          □

В дальнейшем будем предполагать, что условие (24) выполнено. Тогда из (23) получаем

к

или

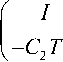
y = Y a + C T_{1 2}z + Cf , z = Z в + C 2 T 21 y + C 2 g ,

у1=I z J к f H

+

Э Г y 0 Э •

21   ^^22 J

H 12 Э Г'

к ^H 21   ^H 22 J

•

к ⁰ C 1 0

Z J 0 Э

2 J

•

Г а Э \ в j f f Э к g J ’

+

0 '

Z J

f a Э

+

^{к вJ} (23)

где

H 11 =( I — C 1 T 12 C 2 T 21 ) ^{— 1}; H 12 = — ( I — C 1 T 12 C ₂ T 21 ) ^{— 1} C 1 T 12 ; ₍ 26)

H 21 = C 2 T 21 ( I — C 1 T 12 C 2 T 21 ) ^{— 1}; H 22 =( I — C 2 T 21 C 1 T

Таким образом, общее решение f У Э _ _ .        .

x = I Ie DS ( m ) х FD ( a )   системы (21)

к z J

где I – единичный оператор в соответствую-

имеет вид:

щем пространстве.

Для получения представления общего решения системы (21) и записи равенств, определяющих фундаментальную матрицу и оператор Коши системы (21), решим (23) относитель-

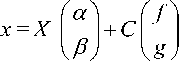
фундаментальная матрица X связана с фундаментальными матрицами Y и Z равенством

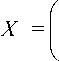
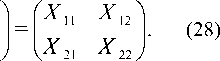
Оператор Коши C выражается через операторы Коши C и C равенством

нено условие (33), где ( N x N ) -матрица £Х определяется равенствами (32),(31),(28),(26).

C =    ^{11  1}

l H 21 C 1

H 12 C 2

H 22 C 2

f C ¹¹

l C 21

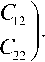
5. Задачи управления для гибридных моделей

Запишем гибридную систему (21) в виде

S x = 0 x + ^ ,            (34)

4. Краевые задачи для гибридных моделей

Общей линейной краевой задачей называется система (21) вместе с линейными ограничениями

где x = I y Ie DSⁿ ( m ) x FD ^v ( д ) , l z I

I f I

^ = 1

l g 7

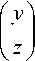
Y e R N ,

0 =

i TT

T 11

TT

V 21

, S x =

22 7

I : DS” ( m ) x FD ^v ( д ) ^ z I

где I : DS n ( m) x FD ^v ( д ) ^ R N - линейный

ограниченный вектор-функционал, имеющий

представление:

^ Lⁿ x FD ^v ( д )

и рассмотрим гибридную систему управления

S x = 0 x + Fu + ^.               (35)

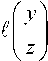
T

= f Ф ( s ) y ( s ) ds + T ₀ y (0)

J 0

+

m                д

+Z* k Дy T) + lXjZ (/Д k=1                 j=0

Здесь T^ , k = 0,1,..., m - постоянные

( N x n ) -матрицы; Г_;., j = 0,1,..., д - посто

янные ( N x v ) -матрицы; Ф - ( N x n ) -матрица

с измеримыми и ограниченными в существенном на [0, T ] элементами. Предполагается, что компоненты £_t : DSⁿ ( m) x FD ^v ( д ) ^ R , i = 1,... , N , вектор-функционала I = col(£ p.. .,£ ^) линейно независимы.

Отметим, что в виде выражения (31) может быть записана, в частности, совокупность начальных условий y (0) = y₀ и условий на величину скачков y ( t ) = A ( t ) у ( T — 0) + Y и др., встречающиеся во многих работах [см., напр.: 22].

При условии N = n + mn + v краевая задача (21),(30) однозначно разрешима при любых f , g тогда и только тогда, когда ( N x N ) -матрица

С.X = ( УХ ¹,..., УХ ^{n + mn + v} ) , (32) где X ^j – j -й столбец X , невырождена, т. е.

det £X ^ 0. (33)

Здесь u e H - управление, H - гильбертово пространство со скалярным произведением ^-,^ , F : H ^ L” x FD^v ( д ) - линейный ограниченный оператор, отвечающий за реализацию управляющих воздействий на систему. Зафиксируем целевой вектор-функционал £: DSⁿ ( m ) x FD^v ( д ) ^ RN , представленный в виде (31). Назовем задачей управления относительно заданной системы ограниченных функционалов £ j c col(£,,...,£ ^) = £ для гибридной системы управления (35) задачу

S x = 0 x + Fu + ^ ,

x (0) =

I y ⁽⁰⁾ I l z (0) J

f ^a Ъ R^{n + v} ; Ух = у e R^N l в J

как задачу выбора такого управления u e H , что краевая задача

S x = 0 x + Fu + ^ ,

x (0) =

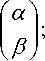
£x = у

Таким образом, справедлива

Теорема 1: Пусть N = n + mn + v . Тогда краевая задача (21),(30) однозначно разрешима при любых f , g тогда и только тогда, когда выпол

разрешима. Если такое управление существует для любых p e L ” x FD ^v ( д ) , a e Rⁿ , в e R ^v , Y e R N , то гибридная система управления (35) называется управляемой относительно вектор-функционала .

Получим условия разрешимости задачи управления (36) используя равенство (27), дающее представление всех решений (35) с начальными условиями у (0) = a e Rⁿ , z (0) = в e R ^v :

a x = X a + Cp + C Fu.

Здесь a = col (Ay (rI),..., Ay (rm ) ) e Rm" - произвольный вектор. Применяя вектор-функционал к обеим частям (38) и учитывая цель управления – доставление заданному функционалу £x значения у e RN на траекто- риях, определяемых системой (36), получаем уравнение

a

£X a + £ C p + £C Fu = у

относительно a e R^mn и u e H .

Сведем (39) к системе линейных алгебраических уравнений. Заметим, что поскольку A = £jC F - линейный ограниченный функционал, определенный на гильбертовом пространстве H , то найдется такое v. e H , что

*                    *

A = X, -, u} (где Vj = ( CF ) £_j9 знак ’ используется для обозначения сопряженного оператора).

Будем искать управление u в виде линейной комбинации

N u = E dv i =I

(напомним, что гильбертово пространство H может быть представлено как прямая сумма Sp(vi,...,VN)Ф[Sp(vi,...,VN)], где  Sp(-) - линейная оболочка соответствующих элементов). Получим, что

£ C Fu = Vd ,                     (40)

где V = {(v.,v.)}       - (N x N) -матрица j'H, j=I,..., N

Грама для системы v₁,...,v_N eH .

Запишем матрицу X в форме tX = (sy | Sa 15z),               (41)

где размерности матриц   s_y , s_A

( N x n) , ( N x ( mn )) и ( N x v ) соответственно.

Таким образом, вопрос о разрешимости задачи управления сведен к вопросу о разрешимости системы линейных алгебраических уравнений sAa + Vd = y — ^Cp - s ya - s zP (42) Сформулируем этот результат в виде следующей теоремы.

Теорема 2 (ср. c теоремой 2 [30]). Задача управления (36) для гибридной системы управления (35) разрешима тогда и только тогда, когда система линейных алгебраических уравнений (42) разрешима относительно (mn + N) -вектора col (a, d) . Каждое решение col (a, d0 ), a0 = col (01,..., 0^ ) системы (42) определяет управление, решающее задачу (36), содержащее импульсы Ay (rk ) = ak, k = I,...,m, и управление u e H, u=EN=idojvj-

• 6.    Доказательный вычислительный эксперимент

Эффективное исследование поставленной задачи (краевой задачи (21),(30) или задачи гибридного управления (36)) основывается на исследовании системы линейных алгебраических уравнений (СЛАУ), X • c=y для краевой задачи и (42) для задачи управления. Очевидно, что коэффициенты этих систем могут быть найдены только приближенно. Поэтому исследование разрешимости СЛАУ требует использования специальной техники: так называемого доказательного вычислительного эксперимента (ДВЭ) [1, 2, 27, 18]. Как теоретические основы, так и практическая реализация ДВЭ требуют разработки специальных конструктивных методов, основанных на фундаментальных утверждениях общей теории и современном программном обеспечении. Основная задача таких методов – установить факт разрешимости задачи. Затем, если это удалось, построить приближенное решение с гарантированной оценкой погрешности. ДВЭ как инструмент исследования дифференциальных и интегральных моделей активно разрабатывается в течение последних двадцати лет. Существует несколько основных направлений исследования в этой области: изучение задачи Коши для обыкновенных дифференциальных уравнений (ОДУ) и для некоторых классов уравнений в частных производных (УЧП) (H. Bauch, M. Berz, G. Corliss, Б.С. Доб-ронец, E. Kaucher, W. Miranker); изучение краевых задач для ОДУ и УЧП (С.К. Годунов, Н.А. Ронто, А.М. Самойленко, M. Plum); изучение интегральных уравнений (С.А. Колмыков, Ю.И. Шокин, З.Х. Юлдашев, R. Moor). Общая идея, лежащая в основе этих исследований, заключается в выполнении интервальных вычислений в конечномерных и функциональных пространствах и применении специальной техники округления в ходе вычислений. Используемый нами подход [1,18] позволяет рассматривать существенно более широкий класс задач, имеющих такие особенности, как нелокальность операторов, наличие разрывных решений, наличие оператора внутренней суперпозиции, краевые условия общего вида. Кроме того, при та- ком подходе не используются интервальные вычисления, для которых характерен быстрый рост длины результирующего интервала. Вместо этого используется арифметика рациональных чисел со специальной техникой направленного округления. Основная идея конструктивного подхода заключается в том, что для исходной задачи строится приближенная задача с точно известными параметрами, которые позволяют провести доказательную вычислительную проверку условий разрешимости. Если приближенная задача разрешима, итоговый результат зависит от близости к ней исходной задачи (напомним, что неравенство || EX — XX ||<1/||[XX ]-1 || для приближений

, X к , X , означает, что X обратима). Теоремы, лежащие в основе ДВЭ, допускают эффективную компьютерную проверку условий разрешимости исходной задачи. Если эти условия не выполняются, приходится строить новое, более точное приближение исходной задачи, и снова проверять эти условия. Реализация конструктивных методов в виде компьютерной программы (разумеется, такая программа ориентирована на строго определенный класс задач) позволяет изучать конкретную задачу, многократно повторяя ДВЭ. Теоретическое обоснование и детали практической реализации ДВЭ для изучения функциональнодифференциальных систем представлены в [18]. Ясно, что ДВЭ подразумевает построение и достаточно точную аппроксимацию основных параметров СЛАУ с гарантированными оценками погрешностей. Эффективная доказательная (компьютерно-ориентированная) техника таких построений для определенных классов функционально-дифференциальных уравнений предложена в [31] (см. также [27]).

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант № 10-01-96054.