Гибридный численно-аналитический подход для моделирования антиплоских колебаний многослойных упругих волноводов с множественными неоднородностями

Компьютерное моделирование процессов распространения и рассеяния бегущих упругих волн в слоистых материалах с единичными или множественными неоднородностями (препятствиями, структурными дефектами, источниками колебаний, сенсорами и другим) является типичной задачей для многих приложений, таких как ультразвуковой неразрушающий контроль и мониторинг состояния конструкций [1 –4] , сейсмическое зондирование [5, 6] , сенсорика [7 –9] и других [10 –13] . Численное решение указанных волновых задач может быть построено в рамках методов, базирующихся на сеточной аппроксимации области исследования (методов конечных разностей и конечных элементов (МКЭ)) или ее границ (метода граничных элементов). Широко доступными являются специализированные программные комплексы, реализующие эти методы с учетом геометрии задачи и комбинации материалов. Среди них можно выделить МКЭ-пакеты ANSYS, COMSOL, ACELAN, Fidesys. Однако использование МКЭ требует существенных вычислительных затрат при рассмотрении волновой динамики протяженных структур с неоднородностями, что связано с необходимостью уплотнения сетки в окрестности препятствий сложной формы (в особенности при наличии угловых точек) и уменьшения размера элемента сетки с ростом частоты колебаний. Кроме того, стандартный МКЭ применяется для расчета волновой динамики тел конечных размеров. Для моделирования же оттока волновой энергии на бесконечность из области, содержащей дефекты (препятствия), требуются другие подходы, например, поглощающие граничные условия в форме идеально согласованных слоев (Perfectly Matched Layers — PML) [14, 15] или поглощающих слоев с возрастающим демпфированием [16] . Подобного рода подходы зачастую также реализованы в современных конечно-элементных пакетах.

Стандартный МКЭ не дает возможности анализировать распределение энергии между отдельными бегущими упругими волнами для получения физически наглядной волновой картины процессов возбуждения, распространения и рассеяния волн на единичных и множественных локализованных препятствиях. Для выделения отдельных волн из общего численного МКЭ-решения могут использоваться условия обобщенной ортогональности нормальных мод [17, 18] . Такой подход был реализован в случае однослойных плоских и трехмерных волноводов [19 –21] .

Естественными способами преодоления проблем, связанных с высокими вычислительными затратами и необходимостью дальнейшей нетривиальной постобработки МКЭ-результатов для изучения волновой структуры решения задач, являются те из них, которые базируются на гибридных сеточно-аналитических вычислительных схемах. При этом решение в конечной области, содержащей неоднородность, строится численно, например, МКЭ, а затем в примыкающих к ней полубесконечных частях волновода стыкуется с физически наглядными представлениями волновых полей в виде суммы бегущих волн; присутствующие в них амплитудные множители в зависимости от геометрических характеристик и механических свойств рассматриваемых материалов имеют

аналитический вид [22] или ищутся численно с использованием матричных методов [23] , полуаналитического интегрального подхода [24, 25] или подхода с полуаналитическими КЭ (Semi-Analytical Finite Elements — SAFE) [26 –29] , учитывающими отток волновой энергии на бесконечность [30] . Гибридные схемы подходят и для изучения волноводов с несколькими препятствиями, между которыми располагаются протяженные однородные участки [31, 32] , однако в таких задачах требуется их самостоятельная реализация в стандартных МКЭ- и SAFE-подходах, что ограничивает их распространение в инженерной практике.

Обсуждаемая в данной статье сеточно-аналитическая схема является дальнейшим развитием гибридного подхода, предложенного в работах [24, 25] . Ключевая особенность последнего состоит в том, что вместо построения глобальной матрицы, в которую одновременно входят блоки, соответствующие КЭ-аппроксимации локальных областей с неоднородностями и аналитическим представлениям волновых полей в полубесконечных частях волновода [28, 29] , осуществляется их сшивка в два этапа. На первом этапе решается набор независимых вспомогательных краевых задач для локальной области с граничными условиями на поперечных гранях, отвечающими полю смещений или напряжений для отдельных распространяющихся или затухающих мод. Для решения таких задач может применяться любой стандартный МКЭ-пакет, что дает возможность как задавать произвольную сложную геометрию неоднородностей внутри области, так и использовать связные мультифизические модели, позволяющие, например, анализировать возбуждение колебаний пьезоактуатором с учетом пьезоэффекта и его электромеханической связи с подложкой [2] . На втором этапе полученные МКЭ-решения сшиваются с представлениями волновых полей в протяженных областях в виде суперпозиции бегущих и затухающих нормальных мод с учетом для них обобщенных условий ортогональности.

В настоящей работе производится продвижение данного подхода на задачи возбуждения, распространения и рассеяния SH-волн в многослойных волноводах, содержащих произвольное конечное число локальных областей, в которых могут находиться не только препятствия, но и источники колебаний (актуаторы) или сенсоры, разделенные протяженными однородными участками. В таком случае разработанная схема позволит, например, для задачи «источник колебаний–препятствие–сенсор» оценить вклад в отклик сенсора каждой отдельной моды с учетом особенностей ее возбуждения актуатором заданного типа и рассеяния на локализованных неоднородностях.

Для ознакомления с методом и иллюстрации получаемых на его основе результатов в рамках данной работы рассматриваются антиплоские колебания многослойного прямоугольного волновода со множественными неоднородностями. Во втором разделе дается детальное описание предлагаемой модификации гибридного численно-аналитического подхода [24, 25] в общем виде и приводятся результаты его численной верификации. Кроме того, указываются пути оптимизации вычислений и сопоставляются вычислительные затраты в рамках МКЭ с идеально согласованными слоями (МКЭ-ИСС) и гибридного подхода. В третьем разделе демонстрируются возможности гибридного численно-аналитического подхода для анализа волновой структуры решения на примере классической для ультразвуковой волновой диагностики задачи «источник колебаний–препятствие–сенсор».

• 2.    Гибридный численно-аналитический подход для случая множественных неоднородностей

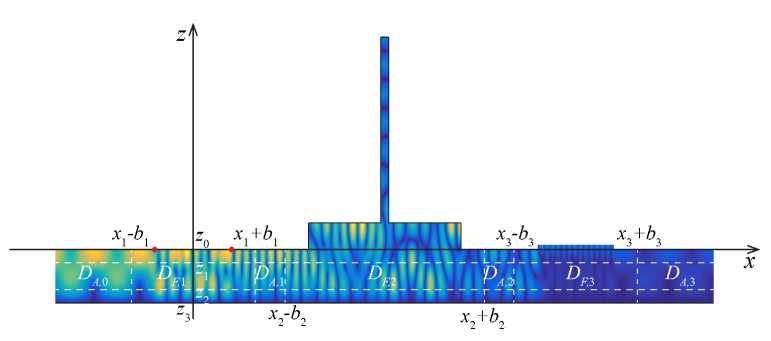
Рассматриваются установившиеся антиплоские гармонические колебания u (x,z) e^-^ (гармонический множитель e -i^ далее опущен) многослойноговолновода W = { (x,z): | x | <  ж , z _M <  z <  z ₀ } (Рис. 1 а ), состоящего из M изотропных слоев W m = { (x,z): | x | <  ж , z m <  z <  z m - i } и содержащего K локальных неоднородностей (источников колебаний, полостей, выемок, ребер жесткости, различных дефектов). Неоднородности выделяются в отдельные ограниченные области D F,k = { (x,z) : (x k — b k ) k + bk), z_M< z< z_Q}, k =1,...,K (Рис. 1 б), решение внутри которых в дальнейшем предполагается искать численно. Здесь xk — центр области, включающей неоднородность шириной 2bk, ak определяют ее точные границы вдоль оси Ox. Оставшиеся части волновода считаются однородными и описываются в следующем виде:

D a, q = { (x,z): x <  x i - b i , z m <  z <  z q } ,

D A,k = { (x,z): (x k +b k ) <  x <  (x k+1 — b k+i ),z M <  z <  z q } , k =1,...,K — 1, D a,k = { (x,z): x >  x k + Ь к , z m <  z <  z q } .

Антиплоские колебания волновода при отсутствии внешних объемных сил и внутренних источников колебаний для каждого отдельного слоя W i представляются уравнениями Гельмгольца относительно смещений u i :

Au i (x,z) + K ² u i (x,z) = 0,   i = 1,...,M.                                     (1)

Здесь K i = ш/ci , ш — круговая частота, c i — скорость распространения волн сдвига (S-волн) в i -м слое.

На внутренних границах слоев задаются условия непрерывности смещений и напряжений:

u i ^l z=z i    u ^{i+1 l} z=z_i ,

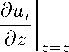
du i+i ∂z

i = 1,...,M — 1.

В отдельных областях D F,k могут находиться источники колебаний. Для определенности предполагается, что источники колебаний приложены к верхней границе волновода и описываются функциями вида q k (x) ,

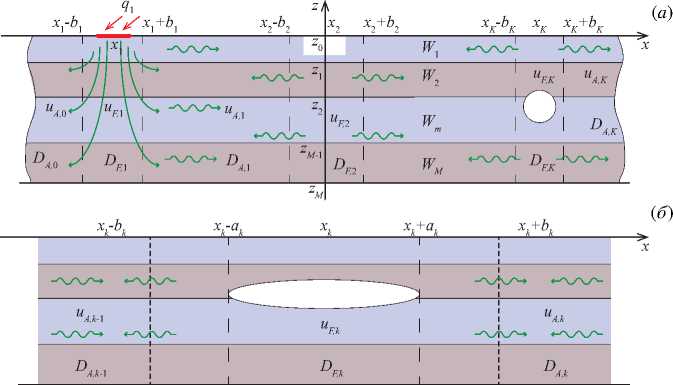
Рис. 1. Многослойный волновод с произвольными неоднородностями ( а ); ограниченная область D F,_k с неоднородностью в виде внутренней полости ( б )

| x - x k | С a k . Остальные точки поверхности z = z ₀ считаются свободными от напряжений. Нижняя граница считается жестко закрепленной:

^du i (^x,z) = XJj^x)  z = z _o , U m (x,z) = 0, z = Z M ,

^dz     k=1

где 6 k = 0 , если внутри области D F,k отсутствуют источники колебаний, и 6 k = 1 , если они присутствуют. Для выделения единственного решения сформулированной краевой задачи (1) – (3) добавляются условия излучения в виде принципа предельного поглощения [33, 34] .

В рамках гибридного подхода [24, 25] общее решение краевой задачи (1) – (3) с учетом того, что в K областях содержатся препятствия, имеет вид:

K

u(x,z)= U A,o (x,z)+y^ U F,k (x,z)+U A,k (x,z).                               (4)

k = 1

Здесь u F,k — численные решения в областях D F,k , для построения которых используется МКЭ, а u A,k — набор аналитических решений в областях D A,k без неоднородностей (Рис. 1) . За пределами этих областей решения считаются равными нулю. Таким образом, конкретной точке волновода соответствует одна из функций суммы (4) .

Аналитические решения u A,k представимы как суммы бегущих волн:

U A,k (x,z) = X “ Jo k c +,n d n (z)e i ^Z n ^{(x - xk - ak)} +6 Kk <^ i^ d n ^ z. ^{- z x x} ■ ' ^+a ■ ' ,             (5)

где d_n(z) — форма волны, обусловленная волновым числом Z n , для ее получения в данной работе используется полуаналитический интегральный подход [33] . При этом 6 ij = 1 , если i = j ,и 6 ij = 0 , если i = j . В (5) c + n , c ^-+ ₁ n — неизвестные константы, характеризующие амплитуды волн с номером n в k -й однородной области. В случае, когда в волноводе имеется единственная область с неоднородностью ( D F, ₁ ), решение вида (4) упрощается до суммы, состоящей из трех слагаемых [24, 35] .

Среди волновых чисел ζ n для конкретного значения частоты ω можно выделить конечный набор вещественных волновых чисел n = 1, 2 ,...,N r и бесконечный набор чисто мнимых значений n = N r + 1, N r + 2,... [34] . Слагаемые в разложении (5) с вещественными волновыми числами соответствуют незатухающим нормальным модам, распространяющимся вдоль горизонтальных границ волновода. Данные моды описывают отток и приток волновой энергии от областей с неоднородностью. Слагаемым с мнимыми значениями ζ _n отвечают волны с экспоненциально затухающими амплитудами при удалении от областей с неоднородностями:

d n (z)e ± i^z n ^{( x -( x} k ± ^a k )) | - O ^ e ^{-Im Z} n ^{| x -} (^x k ± ^{a k} ) l ) , k = 0,1,...,K,   (x,z) G D A,k .

Последнее соотношение справедливо для любого волновода конечной толщины (однослойного и многослойного, изотропного и анизотропного, с вязкостью или без нее), что делает гибридный подход применимым и в данных случаях. Указанное свойство позволяет ограничить в разложениях (5) число слагаемых до N > Nr и определить границы раздела областей: локальных, содержащих неоднородности, и протяженных однородных (за счет значений параметров bk , Рис. 1). Увеличение количества удерживаемых мод или/и расширение областей с неоднородностью приводит к повышению точности решения рассматриваемой задачи, но одновременно и увеличивает вычислительные затраты при его построении. Для достижения приемлемой точности вполне достаточно удерживать в разложении два слагаемых с мнимыми значениями Zn (N = Nr + 2) и отходить от границ препятствия на расстояние, равное двум толщинам волновода: bk = ak + 2H, где H = z0 — zM [24,25].

Численные решения u _F,k представляются в виде суммы МКЭ-решений в областях D _F,k со специальными граничными условиями на поперечных гранях областей:

u F,k ⁽x^,z) = S k u F,k,0 ⁺ ^_n=1 ^ 0k-1 C k-₁,_n u _F,_n,_k, ₁ ⁺ c — n ^{u -},n,k,2 ^{+ c}tn u ⁺ ,n,k,1 ^{+ S} Kk c k + 1,n^UF,n,k,2 ,

(x,z) G D f,- .

Решения вида u _—,_k, ₀ описывают приток волновой энергии от источников колебаний внутри области D f,- в волновод. Подобного рода конечно-элементные модели всегда добавляются при наличии источников колебаний внутри локальных областей. Решения u F _{nk 2} , u + _nk 1 обозначают отток энергии от области D F,_k , а u F _{nk 2} и u ^—_{n k} 1 — приток энергии от соседних областей с неоднородностью ( D _f , _-+1 и D _F,_{k -1} соответственно). В случае единственной области с неоднородностью решения u + _{n k 2} и u ^— _{n k} 1 отсутствуют, что согласуется с результатами, полученными ранее в [24, 25, 35] . С учетом данных обозначений на границах локальных областей условия для МКЭ-решений формулируются в следующем виде:

^— I                    р1- П п( Ь _к — а_к)

^u —,n,k,2l       , = d n e

I x=x k —b k

^—       I          __ Л ii Cn x k F ^{— b} k ^{— x} k - i ^{— k} k - i ⁾

^u F, n, k, 1 |         , = d n e

I x=xk-bk uF,n,k,1

x=x k +b k

=0,

u F,n,k, 2

x=X k + b k

=0,

(du—,n,k,1/dz) z z =0,     (du—,n,k,2/dz) z z =0, uF,n,k,1

।        =⁰,

I Z — Z M

u F,n,k, 2

=0,

uF,k,0 | x=xk — bk =0, u—k0 1 x x +bk =0, (duF,k,o/dz)1 z—z0=qk(x), uF,k,0 1 z z. =0,

u +

F,n,k, 1

_u +

F,n,k, 1

-b _k

=0,

_u +

F,n,k, 2

^x — ^x k ^{— b} k

=0,

= d e^ n ^b k a k )

■^— x k + b k

u ⁺

F,n,k, 2

= d ^^^Zn ( ^x k +i ^{— k} k +i ^{— x} k ^— b k ⁾ = x _k + b _k

Wnkjw  = ⁰,

^{( du} F,n,kX ^{/ dz )} \z= 0 = ⁰,

u F ⁺ ,n,k, 1

I       =0, z =z.

u F ⁺ n k 2

= 0.

На внутренних межслойных границах предполагается выполнение условий (2). Для численного решения краевых задач (1), (2), (7) может использоваться любой стандартный пакет конечно-элементного моделирования. В настоящей работе для применяется COMSOL Multipysics 5.6.

Следует отметить существование связи между u — _{n k} 1 и u — _{n k 2} , а также между u —, _{n k} 1 и u —, _{n k 2} . Эти конечно-элементные решения различаются между собой только граничными условиями на левой ( x = x _k — b _k ) и правой ( x = x _k + b _k ) поперечных гранях волновода, причем различия содержатся лишь в постоянном множителе:

u F ⁺ n k 2

u F n k 1

-b k

__i ^Z n ^(x k ^{+ k} k ^{— 2b} k ^{— x} k - 1 ^{— k} k — 1 ) „ .^—

= e                       u F n k 2

x = x k —b k

x = x k + b k

= ei C n (x k +i —k k +i —x k —2b k +k k )

u F n k 1

.

x = x k + b k

Граничные условия вида (7) и представления (4) – (6) обеспечивают выполнение всех условий краевой задачи (1) – (3) .

Кроме того, благодаря им на границах раздела ( x = x _k ± b _k ) выполняется непрерывность как локальных численных (6) , так и глобальных аналитических (5) смещений. Неизвестные константы c = (c ^— 1 ,...,c ^— _n ,c + 1 ,...,c +_n ,...,c K _n ) ^T определяются исходя из дополнительных условий непрерывности напряжений на поперечных границах локальных

областей:

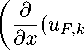
^{— u} A, k — 1 )

k

-

b k

=0,

^{— u} A, k )

= 0. x _k + b _k

Дискретизация соотношений (9) для построения системы линейных алгебраических уравнений относительно вектора неизвестных констант c может быть проведена различными способами. В рамках данной работы используется метод Галеркина. В качестве проекторов выступают функции d _n (z) , где n= 1,...,N , обладающие свойством ортогональности скалярного произведения в пространстве L 2 [17, 18] :

z 0

const, i = j, 0, i= j.

(d i ,d j ) = d i (z)d j (z)dz =

Проектирование каждого уравнения (9) на выбранную систему приводит к системе линейных алгебраических уравнений относительно неизвестных констант размерности 2NK х 2NK :

Ac = f .

Матрица A в (10) представляется в виде разности двух блочных матриц: A = D — B . Для описания элементов и блоков этих матриц вводятся дополнительные обозначения:

z 0

Inm = jdn(z)dm (z)dz, enk = e1^-ak \ e±ki = e±iZn(xk Bbk-(xl±ai)), z3

±∓ klnm		f du F,m,k,l ( x k ± b k ) , i =           ∂x        d n ( z ) dz,				z 0 I ±n = / ■'       ■ ХХЖ
		z 3				z 3
		^1  •••		±∓ I kl 1 N		/ ±iZ 1 e 1k I 11    •••		0
±^— 1 B kl =		. . .	. . .	. . ,	D k± =	1                                  .                                  . .. ..		. .	j ,
		±∓ I klN 1		±∓ I klN N		\        0           •••	± iZ N e Nk I NN
				( ± iz 1 ±. l	I 11     ••	•             0          \
			D k±l	— 1             . .	. .	. . ..	.
				0	••	•   ± iZ N e Nkl I NN /
С их учетом матрицы D , B принимают вид:
			(D .	...        0 ..	0 .	0        0        ... ..	0 >  .
		D =	. 0 0 .	.. D + ...    D kk-1 ...        0 .	. D k- 0 .	.                 .               ... 0         0         ... D +   - D k    D kk+1    ... .                        ..	. 0 0 .	,
			. 0	...             . ...        0	. 0	..  . 0        0        ...	. DK /
	( B -- b + - .	B -1 + B .	B -2 + B .	•••        0 •••        0 ..	0 0 .	0      0       ... 0      0       ... ...	0 0 .	0 0 .	0 0 .	j
B —	. 0 0 .	. 0 0 .	. 0 0 .	.. •••   B k- 1 - •••   B+r ..	. B k- 2 - B .	..   . B -1 +  B    - R+ +   r++ B k 1     B k 2     ••• ...	. 0 0 .	. 0 0 .	. 0 0 .
	. 0 0	. 0 0	. 0 0	.. •••        0 •••        0	. 0 0	..   . 0      0       ••• 0      0       •••	. B K-- 1 B K1	. B K-- 2 B K	. b k + R++ B K 1	)

Вектор правой части в (10) представляется как набор скалярных произведений МКЭ-решений u _F,_k, ₀ и функции формы волны d n ( z ) :

,                 .            .               .            .               .             \ т

X. --     X- --   х. т+ х. т+   л -~ х_. т+ f — ( ^11011 ,...,^1I01N,^11011 ^..^lIQlN,^2I021,...,^KI0KN ) .

Решение системы (10) определяет значения неизвестных констант — компонент вектора c , а значит, и вид локальных и глобальных решений (5) , (6) . В силу линейности исходной краевой задачи сформулированное решение вида (4) справедливо не только для смещений, но и, например, для напряжений.

Для численной верификации развиваемого гибридного численно-аналитического подхода рассматривается модельная задача об антиплоских гармонических колебаниях трехслойной полосы

( M = 3 ) алюминий/сталь/алюминий общей толщиной H = 2 мм, лежащей на недеформируемом основании (Рис. 2) . Слои алюминия имеют одинаковые толщину h al =0.5 мм, модуль Юнга E al = 69 ГПа, коэффициент Пуассона v = 0.32 и плотность р = 2700 кг/м ³ . Слой стали, располагающийся между слоями алюминия, считается изотропной средой со следующими параметрами: h = 1 мм, E = 210 ГПа, v = 0.3 , р = 7800 кг/м ³ .

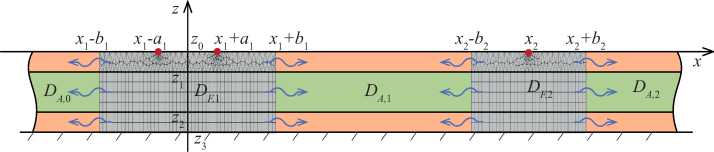
Рис. 2. Геометрия модельной задачи

В рамках модельной задачи неоднородностями являются поверхностные источники колебаний, расположенные в точках с координатой x : x = x 1 — a 1 , x 1 + a 1 , x ₂ (точка x 1 совпадает с началом координат). В таком случае в волноводе W выделяются две локальные области — D F,1 и D F,2 (Рис. 2) , и функции q k имеют вид: q 1 (x) = 5 (x — x 1 + a 1 ) — 5(x — x 1 — a 1 ) и q ₂ (x) = £(x — x ₂ ) , где 5(x) — дельта-функция Дирака. Остальные условия краевой задачи (1) – (3) не изменяются.

Численные результаты, полученные с использованием предлагаемого обобщения гибридного подхода (4) – (6) , сопоставляются с результатами двух других подходов. Первый из них — численное решение в рамках МКЭ с идеально согласованными слоями (МКЭ-ИСС), моделирующими отток волновой энергии на бесконечность [14, 15] . С учетом геометрических особенностей рассматриваемой модельной задачи для ее решения также может применяться полуаналитический интегральный подход [33, 34, 36] и техника интегрального преобразования Фурье:

u Int

+ ∞

(x,z )= у

k (x — ^,z

-∞

)q (€ M = I

Γ

K (a,z)Q(a)e ^{- iax} da,

q (x) = (5(x — x i + a i ) — 5(x — x i — a i ) — 5(x — x 2 )) • 10 ^-3 , Q(a)= (e ^{ia ( x} 1 ^{- a} 1 ) — e ^{ia ( x} 1 ^{+ a} 1 ) — e^{i ax}^ • 10 ^-3 .

Здесь k (x,z) — функция Грина для многослойного волновода, q (x) — поверхностная нагрузка, а K (a,z ) и Q(a) — их Фурье-символы; контур интегрирования Г почти всюду совпадает с вещественной осью параметра интегрирования α , отклонения от нее имеют место лишь при обходе вещественных полюсов ζ n в соответствии с принципом предельного поглощения.

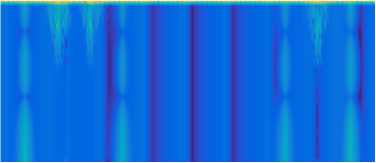
Решение в рамках интегрального подхода в пределах заданной погрешности рассматривается в качестве эталонного. При вычислении значений смещений согласно соотношениям (11) относительная погрешность численного интегрирования не превосходит 10 -³ . На рисунке 3 представлены относительные отклонения смещений, в рамках гибридного подхода ( u Hyb ) и МКЭ-ИСС ( u P ML ), от значений, рассчитанных с использованием интегрального подхода, по логарифмической шкале:

z = lg

| u PML - u Int | | u I nt |

z = lg

| u Hyb - u Int | | u Int |

При гибридном подходе и подходе МКЭ-ИСС локальные области дискретизируются прямоугольными КЭ (Mapped Mesh). Степень аппроксимирующих полиномов выбирается равной четырем (Quartic Lagrange), и максимальные размеры d _max каждого КЭ задаются такими, чтобы на минимальную длину волны среди всех нормальных мод на данной частоте колебаний приходилось не менее 8 степеней свободы.

На рисунке 3а, видно, что максимальные погрешности наблюдаются: вдоль верхней границы волновода (z = z0) с резким уменьшением ошибки при перемещении вглубь волновода; в точках приложения нагрузки z, 0 мм

-0.5

-1

-1.5

-2

_ε ( a )

-3

-4

-5

-6

-7

-8

-9

-10

-5     0     5     10    15    20    25    30    35 x , мм

-5     0     5     10    15    20    25    30    35 x ,мм

Рис. 3. Значение относительной ошибки z ( x,z ) на логарифмической шкале при гибридном подходе ( а ) и МКЭ-ИСС ( б )

( x = x 1 ± a 1 = ± 2 мм, x = x ₂ = 30 мм); на границах раздела локальных и глобальных областей ( x = x 1 ± b 1 = ± 6 мм x = x ₂ ± b ₂ = { 26;34 } мм).

Аналогичные относительно высокие значения погрешности на верхней границе присутствуют и в результатах МКЭ-ИСС (Рис. 3б ). Данный эффект определяется асимптотическим поведением Фурье-символа функции Грина [34] : K (a,z) ^ e ^-| “ ^{|| z - z o |} /a при | а |чда .В точках на границе z = 0 интеграл (11) , в отличие от точек внутри волновода, является медленно сходящимся, что вносит дополнительную погрешность в вычисления. Однако ограничение погрешности в рамках интегрального подхода на данной границе не превышается.

Максимумы ошибки около точек приложения нагрузки и постепенное уменьшение погрешности по мере перемещения вглубь волновода связаны с особенностями построения численного МКЭ-решения. Для повышения точности вблизи подобных точек требуется уплотнение сетки и увеличение порядка аппроксимирующих полиномов. Поскольку все сравниваемые подходы для построения локального решения используют МКЭ, то и характер решений на их основе аналогичен друг другу. В рамках гибридного подхода погрешность локализуется возле верхней границы и относительно быстро спадает при увеличении толщины волновода, а при МКЭ-ИСС подходе ошибка наблюдается вплоть до нижней границы с локальными максимумами в окрестности границ раздела слоев стали и алюминия.

Рост погрешности на стыках локальных и глобальных областей объясняется особенностями разложений (5) и (6) , в которых удерживаются решения, соответствующие вещественным волновым числам, и несколько слагаемых с наименьшими мнимыми волновыми числами. Остальные слагаемые с мнимыми числами опускаются. Поскольку данные моды обеспечивают вклад в ближней зоне, то и наибольшая ошибка возникает вблизи границ раздела.

Следует отметить, что для рассматриваемой задачи как МКЭ-ИСС, так и предлагаемая гибридная схема дают решения, близкие к результатам полуаналитического интегрального подхода. Относительная ошибка при применении гибридной схемы в среднем меньше, чем при МКЭ-ИСС. Для более полной верификации гибридного подхода численные результаты сопоставляются в широком частотном диапазоне. Поверхности на рисунке 3 построены для частоты f = 500 кГц.

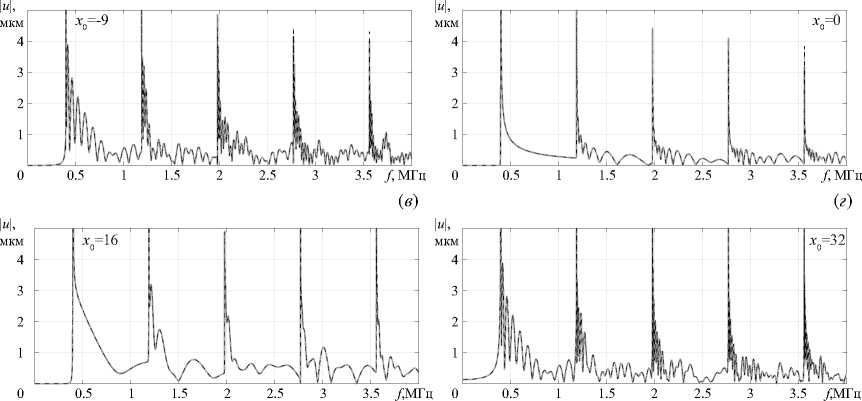
Частотные зависимости спектра модуля смещений в различных точках на верхней границе волновода ( z = z ₀ ) приводятся на рисунке 4. Точки x ₀ выбраны исходя из их расположения относительно локальных ( D F,1 , D f,₂) и глобальных ( D a, ₀ , D a, ₁ , D a, ₂) областей, например, x ₀ = — 9 мм принадлежит области D a, ₀ , а x ₀ = 0 — D _F,1 . Наблюдается практически полное совпадение результатов всех трех подходов. Отличия МКЭ-ИСС от гибридного и интегрального подходов заметны вблизи частот отсечки, которые определяются в спектре смещений в виде резких максимумов (Рис. 4е ). При удалении от точек выхода новых мод колебаний различия уменьшаются

( а )                                                                     ( б )

( д )                                                                     ( е )

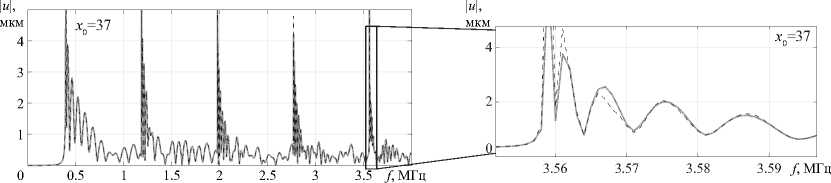
Рис. 4. Спектр модуля смещений | u ( x ₀ , 0) | ( а )-( д ), рассчитанный в точках х ₀ = {— 9;0;16;32;37 } мм на верхней поверхности волновода на основе разных подходов: интегральный подход (сплошная линия), гибридный подход (штрихпунктирная линия), МКЭ-ИСС (пунктирная черная линия); на выноске ( е ) в увеличенном по оси f масштабе показана часть спектра в точке х ₀ = 37

вплоть до практически полного исчезновения. Например, около выхода пятой SH-волны (см. 3.56 МГц, Рис. 4е ) результаты заметно расходятся лишь на интервале шириной 15 кГц.

Описанная версия гибридного численно-аналитического подхода допускает оптимизацию вычислений за счет уменьшения затрачиваемых ресурсов (времени, оперативной памяти). В силу линейности краевых задач соотношения (8) справедливы не только на границах раздела x = xk ± bk, но и в остальных точках области DF,k, а следовательно, в соотношении (6) можно заменить uF- nk 1 на uF- nk 2 и uF+ nk 2 на uF- nk 1. Такая замена позволяет сократить количество МКЭ-решений почти в два раза, что существенно ускорит построение численного решения задачи в рамках гибридного подхода.

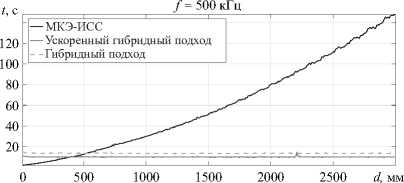
Рис. 5. Время расчета в конкретной точке при частоте f = 500 кГц для двух подходов: МКЭ-ИСС (черная сплошная линия); гибридный без учета соотношений (8) (пунктирная линия); гибридный с учетом (8) (серая сплошная линия)

Результат применения подобной замены в численной реализации гибридного подхода для модельной задачи представлен на рисунке 5. На графике отражена зависимость времени t — продолжительности построения решения задачи, от расстояния d = x2 — x1 между центрами двух областей — DF,1 и DF,2, для разных подходов (МКЭ-ИСС и гибридного подхода с использованием оптимизации и без нее). Видно, что время t в рамках гибридного подхода практически не изменяется при увеличении расстояния d между центрами областей DF,1 и DF,2, поскольку их размеры ограничены значениями параметров b1 и b2 (Рис. 2), а увеличение размера области DA,1 не влияет на время вычислений до тех пор, пока внутри нее справедливо аналитическое представление (5). Сокращение количества МКЭ-задач в гибридном подходе приводит к уменьшению времени построения решения в 1.4 раза, поскольку при реализации задач данные операции наиболее ресурсоемки. При базовом гибридном подходе (без учета соотношений (8)) и выбранной для вычислительных экспериментов частоте f = 500 кГц отыскиваются шесть МКЭ-решений для единственного волнового числа Z1 = 0.607 рад/мм. Моды с мнимыми волновыми числами не учитываются, поскольку при d > 350 мм значения экспонент на правой и левой границах в МКЭ-моделях uF-,n,2,1 и uF+,n,1,2 меньше машинной точности расчета граничных условий, что приводит к появлению ошибки времени исполнения. В рамках оптимизированного гибридного подхода находятся только четыре МКЭ-решения. Время построения одного решения МКЭ-ИСС растет по параболическому закону при увеличении размера области расчета, поскольку расширение области требует добавления новых КЭ для сохранения исходной точности. Для корректного сопоставления времени, затрачиваемого на построение решения, вычисления проводились на одинаковой сетке (Рис. 2) и одинаковом порядке аппроксимирущих полиномов (Quartic Lagrange) в среде Comsol Multiphysics 5.6 с модулем «LiveLink to

Matlab» на сервере с ЦПУ Intel Xeon E5-2698 v.3, оснащенном 256 Гб оперативной памяти.

• 3.    Задача «актуатор–препятствие–сенсор»

Для иллюстрации возможностей, возникающих при применении гибридного численно-аналитического подхода, предлагается рассмотреть одну из типичных для ультразвуковой волновой диагностики задач — волновую динамику в системе «актуатор–препятствие–сенсор» для введенного ранее трехслойного волновода алюминий/сталь/алюминий. Поскольку в пакете COMSOL Multiphysics мультифизический интерфейс для моделирования пьезоупругих материалов реализован только для плоских и трехмерных колебаний, но отсутствует для SH-волн, в качестве источника колебаний задается пара точечных поверхностных сил, направленных противоположно друг другу и имитирующих воздействие пьезоактуатора на упругую подложку (в зарубежной литературе модель получила название Pin-Force Model [2] ) (Рис. 6) . Силы располагаются в точках z = z ₀ = 0 , x = x 1 ± a 1 = ± 5 мм, принадлежащих области D F,1 :

( ^du F,i,o / ^dz ) | _z = z₀ = ^P o (^(^{x — x} i ^— a i ) ^— ^(^{x — x} 1 +^a 1 )),

P o =

γh pzt E pzt ε ISA

Y+4

E al h al             d 31 V

Y = F h-- ,   ^£ISA = h--

E pzt h pzt            h pzt

.

Здесь E pzt = 60.55 ГПа — усредненное значение модуля Юнга для пьезокерамики (PIC151 [37] ); h pzt =0.2 мм — заданная толщина актуатора; d ₃₁ = — 174 ^ 10 ^-15 — компонента тензора пьезоэлектрических модулей; V = 70 В — напряжение, подаваемое на клеммы актуатора; E al и h al — модуль Юнга и толщина верхнего слоя волновода, приведенные ранее.

В области D _{F, 2} на поверхности волновода расположено ребро жесткости, выполненное из стали, являющееся препятствием в рассматриваемой задаче. Контакт между таким препятствием и волноводом предполагается либо идеальным (смещения и напряжений на соответствующей границе непрерывны), либо с частичным отслоением правой части ребра жесткости в области

^ = { (x,z) : (x 2 + a 2 — d delam ) < x <  (x 2 + a 2 ), z = Z o } .

( a )

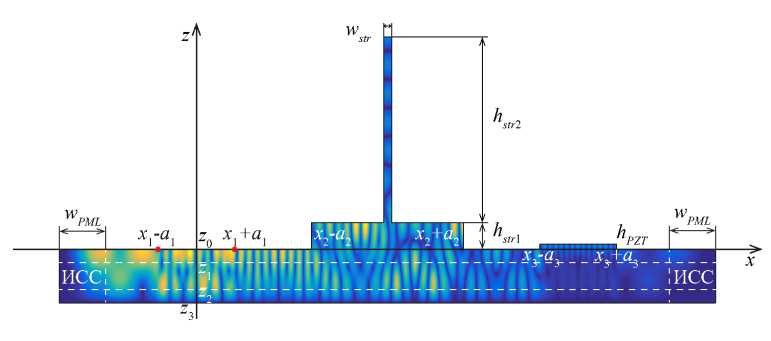
Рис. 6. Геометрия задачи «актуатор-препятствие-сенсор», а также распределение модуля смещений | u ( x,z ) | при частоте f =1 . 5 МГц, вычисленное с помощью разных подходов: гибридный ( a ), МКЭ-ИСС ( б )

( б )

Ширина отслоения ( d deiam = 5 мм) составляет 25% общей ширины контакта ( 2a 2 = 20 мм). Остальные геометрические параметры ребра жесткости (см. Рис. 6б ) имеют следующие значения: w str = 1 мм, h _{str 1} = 1 мм, h _str2 = 7 мм. Параметры стали совпадают с приведенным ранее для серединного слоя волновода.

В области D F,3 на поверхности волновода расположена накладка, имитирующая пьезокерамический сенсор. Параметры материала и геометрические размеры накладки те же, что и у актуатора. Для оценки отклика сенсора V c на распространяющиеся в волноводе упругие колебания применяется соотношение, предложенное в работе [38] :

x 3 +b 3

V c = V o / ^xz ⁰ ) dx, (13) x 3 - b 3

где V 0 — размерный коэффициент, определяющийся электромеханическими свойствами сенсора [38] , для простоты здесь и далее он имеет значение V o = 10 9 В/м.

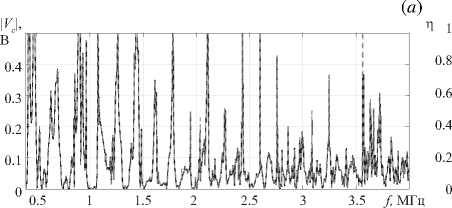
На рисунках 7а , в и 8 а , в представлена зависимость модуля отклика | V c | от частоты f , рассчитанная с использованием подходов МКЭ-ИСС и гибридного. Как и ранее, наблюдается хорошее согласование численных результатов (с небольшими отклонениями вблизи значений частот отсечки или локальных минимумов/максимумов). Вклад каждой нормальной моды в | V c | показан на рисунках 7б , г и 8 б , г . Он находится как n m = | V m | / 1 V c | , где V m — отклик отдельной моды, рассчитывается по формуле (13) , в которой вместо общего поля смещений рассматривается только вклад в него соответствующей нормальной моды с номером m . Для сопоставления влияния отслоения ребра жесткости на отклик сенсора указанные рисунки приводятся парами: рисунки 7 а , б и 8 а , б отвечают условиям без отслоения правой части ребра жесткости, а рисунки 7 в , г и 8 в , г — с учетом отслоения.

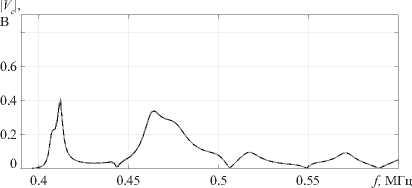
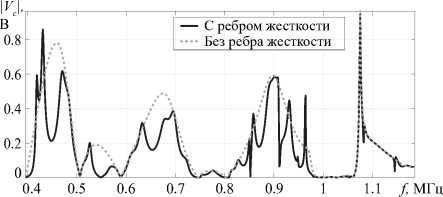
В случае возбуждения единственной фундаментальной SH-волны (от 396 до 1190 кГц) оценить возможность отслоения можно исходя из абсолютных значений отклика сенсора | V c | в некоторых частотных диапазонах. Например, при f G [396,596] кГц максимальные значения отклика при отсутствии отслоения в 2 раза больше, чем при его наличии, что особенно заметно на рисунке 8а , в . То же самое можно сказать и про средние значения отклика в данном диапазоне. Кроме того, наблюдается сдвиг максимальных значений отклика с 432 кГц при отсутствии отслоения (Рис. 8а ) на 412 кГц (Рис. 8в ) при его наличии. В других частотных диапазонах поведение в целом аналогичное, однако при значениях от 808 до 989 кГц имеют место существенные отличия в отклике сенсора, выражающиеся в резких сменах локальных минимумов и максимумов при отсутствии отслоения и в более плавном поведении V c в его присутствии.

С возбуждением последующих фундаментальных SH-волн (после 1.19 МГц) в среднем больший вклад в отклик вносят высшие моды, однако при некоторых частотах моды более низкого порядка по-прежнему являются

( б )

3.5 f, МГц

( г )

( в )

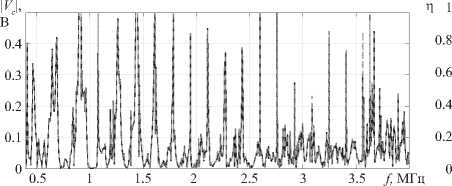
Рис. 7. График зависимости отклика V c на границе раздела сенсора и слоя в зависимости от частоты ( а ), ( в ) (пунктирная линия – МКЭ-ИСС, сплошная линия – гибридный подход); вклад η отдельной бегущей волны в отклик на сенсоре ( б ), ( г ); фрагменты ( а ), ( б ) отвечают идеальному контакту между ребром жесткости и слоем (без отслоения), а ( в ) и ( г ) – при отслоении (12) ребра жесткости от волновода, цифры соответствуют номеру SH-волны

0.5

1.5

2.5

3.5 f, МГц

0.5

1.5

2.5

( а ) | V c |,

В

η ₁

( б )

0.8

0.6

0.4

0.2

1.56

1.58

1.6

0 1.54

1.62 f, МГц

( г )

0.4           0.45           0.5           0.55         f, МГц

( в )

η ₁

0.8

0.6

0.4

0.2

Рис. 8. Часть рисунка 7 на более узком частотном диапазоне

1.54         1.56         1.58

1.6         1.62 f, МГц

доминирующими. Например, как при дефекте, так и без него вклад фундаментальной моды составляет до 99% в отклик сенсора при частоте 1.26 МГц, при которой наблюдается локальный максимум | V c | (см. Рис. 7а , в ). Смена доминирующий моды в отклике сенсора также может служить дополнительным индикатором отслоения. Например, в частотном диапазоне от 1.544 до 1.637 МГц при отсутствии дефекта основной вклад в | V c | дает мода с номером 2 (Рис. 8б ). Однако при частичном отслоении ребра жесткости при указанных частотах преобладает фундаментальная мода 1 (Рис. 8г ). В случае наличия источника колебаний, способного селективно возбуждать отдельные фундаментальные SH-волны [39] , возможно повышение точности детектирования повреждения в рассматриваемой модельной конструкции. Например, большая чувствительность моды с номером 2 к частичному отслоению в частотном диапазоне от 1.54 до 1.64 МГц (Рис. 8б , г ) выявляется при сопоставлении отклика сенсора, полученного в результате последовательного селективного возбуждении отдельных SH-волн.

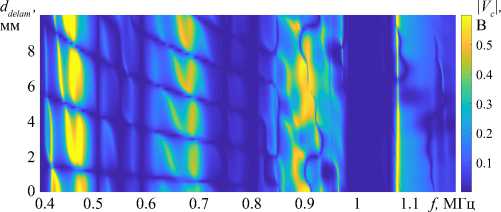
Для более детального анализа влияния частичного отслоения ребра жесткости на отклик сенсора проведены дополнительные расчеты. На рисунке 9а изображена зависимость модуля отклика |Vc | от частоты f и длины отслоения ddelam. Рассматриваемый частотный диапазон (от 396 до 1190 кГц) соответствует возбуждению фундаментальной SH-волны, а величина отслоения меняется от 0 до 50% общей ширины области контакта ребра жесткости и волновода. В указанном частотном диапазоне можно выделить несколько интервалов частот: (396, 850), (850, 980), (980, 1070) и (1070, 1090) кГц, при которых поведение отклика имеет черты, похожие на те, что проявляются при увеличении размеров дефекта. В первом диапазоне частот (от 396 до 850 кГц) заметны линии минимума модуля отклика сигнала. Расположение минимумов в отклике сенсора можно использовать для обнаружения частичного отслоения ребра жесткости, а также для определения его размеров. Следующий частотный диапазон (850, 980) характеризуется достаточно хаотичным поведением отклика при относительно высоких средних значениях. В третьем частотном диапазоне наблюдаются минимальные значения отклика сенсора, практически не зависимые от размера отслоения. При этом минимумы сигнала обуславливаются параметрами самого сенсора (его размерами и свойствами материала), поскольку в третьем частотном диапазоне минимумы сигнала имеют место и в случае отсутствия ребра жесткости между источником колебаний и сенсором (точечная линия, Рис. 9в). В последнем диапазоне отклик при своих средних значениях ведет себя относительно гладко, без ярко выраженных особенностей. В этом же диапазоне частот для оценки меры искажения сигнала в зависимости от величины расслоения рассматривался относительный отклик Vrel в интервале изменения ширины отслоения ddelam:

_{v =} | V c (f,d delam ) - V _c (f,0) |

Vrel |Vc (f,0)| , где Vc (f,0) — отклик сенсора, рассчитанный для идеального контакта между ребром жесткости и волноводом. Полученная поверхность в некотором смысле похожа на поверхность модуля отклика Vc (Рис. 9а), однако траектории локальных минимумов Vrel сдвинуты относительно аналогичных для |Vc | и имеют иную кривизну в частотном диапазоне от 396 до 850 кГц. В других зонах наблюдается некоторое сглаживание отклика сигнала, в том числе в третьем частотном диапазоне (980, 1070) кГц, где ранее присутствовали локальные минимумы.

( a )

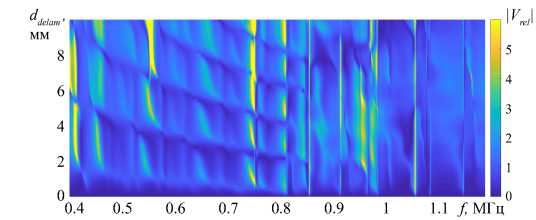
Рис. 9. Поле концентрации уксусной кислоты при k c = 5 · 10 ^-6 м/с в момент времени t = 100 c ( а ); зависимости от полярного угла φ коэффициента поверхностного натяжения ( б ) и напряжения сдвига ( в ) на поверхности капли (исходные и сглаженные данные отмечены, соответственно, цифрами 1 и 2 )

( б )

( в )

• 4.    Заключение

В работе предложено дальнейшее развитие гибридного численно-аналитического подхода для моделирования антиплоских колебаний на случай многослойных волноводов с множественными неоднородностями (дефектами, источниками колебаний, сенсорами), разделенными протяженными однородными областями. Его основное преимущество заключается в возможности исследования волновой динамики протяженных слоистых конструкций, содержащих произвольное конечное число локализованных неоднородностей сложной формы и разной природы при помощи стандартных МКЭ-пакетов, позволяющих учитывать мультифизичность обсуждаемых краевых задач (например, пьезоупругость), без необходимости разработки собственных конечно-элементных решений.

Предложенный подход верифицирован сопоставлением численных результатов решения модельной задачи, полученных с использованием полуаналитического интегрального подхода и стандартного МКЭ. Приведена схема оптимизации вычислений с целью уменьшения затрачиваемых ресурсов (времени счета, оперативной памяти). Показано, что вычисления в рамках гибридного подхода требуют меньшее по сравнению с классическим МКЭ время при удалении областей с локальными неоднородностями друг от друга. Кроме того, рассмотрена классическая для неразрушающего контроля задача «актуатор–препятствие–сенсор». Применение гибридного численноаналитического подхода делает доступной оценку вклада каждой отдельной нормальной моды, рассеиваемой на дефекте в общий отклик сенсора, что важно при выявлении различных дефектов в диагностируемой конструкции. Анализ подобного рода в рамках стандартного КЭ-решения может быть проведен лишь частично, поэтому интеграция разработанного подхода в МКЭ-пакеты позволит сократить вычислительные затраты при расчете волновых процессов в протяженных тонкостенных конструкциях с неоднородностями, а также расширить возможности для проведения более детального анализа волновой структуры получаемых численных решений. К тому же общая схема подхода допускает учет вязкости, что особенно актуально при анализе волновых процессов в композитных материалах.

Исследование выполнено за счет гранта Российского научного фонда № 24-71-00105,