Гибридный подход для краткосрочного прогнозирования временных рядов на основе штрафного P-сплайна и эволюционной оптимизации

Прогнозирование временных рядов является актуальной задачей со множеством приложений в самых разнообразных прикладных областях [1–3].

Однако особенности прикладных задач прогнозирования последних лет во многом обусловлены большими объемами данных. Это связано с растущим использованием GPS, включая информацию от систем позиционирования транспорта и других объектов, с мобильных телефонов, фитнес-браслетов, от датчиков интернет вещей (IoT) и пр. Данные, собранные подобными системами, представляют собой временные ряды (ВР), т.е. наборы числовых последовательностей в хронологическом порядке. Данные ВР всегда рассматриваются как единое целое, а не как отдельные числовые поля [4]. Эти данные динамические, и их анализ позволяет оценить тенденции изменения процесса. На этом и основаны прогностические свойства ВР [5, 6].

В зависимости от числа прогнозируемых значений ВР (горизонт прогноза) выделяют краткосрочное, среднесрочное и долгосрочное прогнозирование. Горизонт краткосрочного прогнозирования включает 1– 3 значения вперед [7] и используется во множестве прикладных областей. Краткосрочное прогнозирование актуально для предсказаний чрезвычайных ситуаций техногенного и природного характера; различных природных явлений; для развития возобновляемых источников энергии и предсказания нагрузок в традиционной энергетике; при расчете скоростей передачи данных оптоволоконных каналов связи; для прогноза спроса, цен и финансовых рынков; при выявлении эпидемических вспышек заболеваемости.

optimization. Computer Optics 2020; 44(5): 821-

Особое место в задачах прогнозирования последнего десятилетия занимают задачи анализа и прогнозирования активности пользователей социальных сетей.

1.    О методах краткосрочного прогнозирования

Существует несколько классификаций методов краткосрочного прогнозирования. Согласно одной из них все методы прогнозирования могут быть разбиты на интуитивные и формализованные методы прогнозирования ВР.

Формализованные методы (часто называемые моделями), в свою очередь, включают в себя статистические и структурные модели прогнозирования [8, 9]. Многие структурные модели основаны на методах искусственного интеллекта.

Согласно [10] методы прогнозирования могут быть сгруппированы в соответствии с параметрическим и непараметрическим подходом. Параметрический объединяет методы, использующие предшествующие знания о распределении данных (экспоненциальное сглаживание, основанные на авторегрессии и скользящих средних). Непараметрический подход не требует в явном виде информации о распределении данных.

По степени использования предшествующих ВР методы разделяются на глобальные или локальные. Локальные методы воспроизводят целые фрагменты ВР на основании их образов в прошлом. Часто используемый при этом математический инструментарий – выборки максимального правдоподобия и локальная аппроксимация. Основное требование этой группы методов состоит в превышении размера выборки над горизонтом прогноза. По разным оценкам от 100 до 700 раз. И поэтому они не применимы в режиме реального времени (РРВ) [9, 11].

Глобальные методы не отыскивают фрагменты квазипериодичности в прошлом, а на основании рекуррентной формулы скрыто используют всю информацию о наблюдаемом процессе. Глобальные методы не явно реализуют идею адаптивного прогнозирования в РРВ.

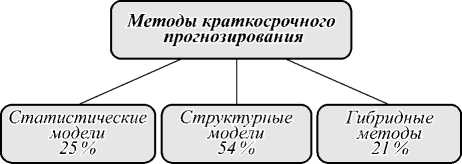
Однако в последние годы появилось достаточно много гибридных методов, объединяющих различные подходы к временному анализу данных. Особенно часто гибридные подходы используются в реальных приложениях. И по данным [10], частота гибридных подходов превысила 21 % против 54% использования непараметрических методов и 25 % параметрических методов. С учетом этого целесообразно группировать методы краткосрочного прогнозирования по трем категориям, приведенным на рис. 1.

Регрессионные модели

Нейросетевые модели на основе

ИНС

Экспоненциальное сглаживание

Авторегрессионные модели

Цепи Маркова

— на основе

" ARIMA

Классификационные деревья

на основе
		SVM

Рис. 1. Классификация методов краткосрочного прогнозирования

Статистические методы основаны на информации о распределении данных для получения моделей прогноза. Это делает методы зависимыми от параметров, оптимизация которых значительно влияет на результаты прогнозирования. По математической сложности статистические методы разделены [4]:

– на модели экспоненциального сглаживания (SES – простое экспоненциальное сглаживание, HES–Хольта и HW – Хольта-Винтерса);

– регрессионные модели основаны на влиянии входных переменных на выходную. Способом реализации регрессионных моделей является преимущественно метод наименьших квадратов (МНК). Нередко используются рекуррентные модификации МНК с учетом весов предшествующих значений ВР;

– авторегрессионные модели основаны на зависимости текущего значения прогнозируемой переменной только от прошлых значений этой же переменной. Наибольшее развитие получила модель ARIMA, включающая этапы авторегрессии, инте- грации и оценки скользящего среднего. Модель ARIMA имеет несколько модификаций: ARIMAX – включает в себя некоторые экзогенные факторы, SARIMA – учет сезонности данных, VARIMA – многовекторные временные ряды.

Структурные модели прогнозирования нередко основаны на методах машинного обучения и не имеют ограничений на характер входных данных. Эти методы проще в настройке, в том числе и для сложных, и для сильно нелинейных ВР.

Существует множество вариантов применения искусственных нейронный сетей (ANN) в краткосрочном прогнозировании. Нейронные сети могут отличаться архитектурой, количеством слоев и нейронов, использованием определенной функции активации или способом обучения. В прогнозировании используются следующие виды ANN:

– сети прямого распространения (feed-forward neural networks);

– рекуррентные нейронные сети (простые RNN, с долгосрочной памятью LSTM, с управляемыми нейронами GRU);

– сверточные нейронные сети.

Основным недостатком ИНН является ресурсо-емкость обучения сети и сложность ее идентификации [11].

Метод опорных векторов (SVM) широко используется в регрессионном анализе и в задачах классификации [12]. В применении к задаче прогноза сложных и нелинейных данных метод SVM требует выбора не простых разделительных плоскостей, а сложных функций ядра. Эти ядра позволяют выполнить отображение входных данных в многомерное пространство признаков. SVM порождает несколько параметров, получаемых чаще всего при решении нелинейной задачи оптимизации с линейными ограничениями.

Название «гибридные методы прогнозирования» достаточно условно. На сегодня эта группа методов наиболее перспективна при создании прогнозных моделей для сложных процессов с переменной и неоднородной структурой [13].

Гибридные методы объединяют в себе особенности методов из различных групп. Обычно один метод выбран из группы статистических, а другой – из структурных. Например, концепции нечеткой логики и вейвлетов [14] или нейронных сетей [15] стали весьма привлекательными для комбинации алгоритмов. Нечеткая логика позволяет уменьшить сложность данных или их неопределенность [16], а вейвлет-анализ выделяет локальные фрагменты нестационарных сигналов [17]. На рис. 1 представлены лишь некоторые, наиболее часто используемые комбинации методов прогнозирования.

Часть гибридных методов является локальными и, как правило, двухэтапными. На начальном этапе временной ряд разбивают на куски структурно однородных фрагментов ВР в соответствии с выделенной ха- рактеристикой или прикладной задачей анализа ряда, например, выделение тренда или сегментация. Далее формируется прогнозное значение на основе комбинации текущего значения ряда и характеристик выделенных фрагментов. Нередко данный подход включает алгоритмы машинного обучения, которые позволяют в процессе прогнозирования использовать различные фрагменты ВР для обучения.

Другая стратегия гибридных методов основана на методах поиска сходства. Алгоритм ближайшего соседа kNN, хорошо зарекомендовавший себя в задачах классификации и кластеризации [12, 18], эффективен и в составе гибридных методов прогнозирования. Вариации алгоритма kNN в комбинации с разными функциями приближения (например, взвешенное или локальное среднее) рядом авторов успешно использованы для нелинейных и сложных временных рядов [19, 20].

При неизвестной модели ВР начальный этап прогнозирования выполняет предобработку данных. И независимо от идей сегментации или кластеризации эффективно работает лишь в апостериорных режимах. Для дальнейшего предсказания данных в РРВ необходима аналитическая модель процесса, допускающая последовательную или рекуррентную реализацию.

При создании модели ВР целесообразно заменить традиционные сложные регрессионные соотношения простыми гладкими функциями аппроксимации. Перспективными с позиции описания локального поведения сложных ВР являются кусочнополиномиальные сплайн-функции. Выбор узлов сплайна для получения его отдельных фрагментов является фактически способом создания паттерна для поиска сходства части ВР в будущем. Кроме того, некоторые виды сплайн-функций допускают реализацию, а соответственно, и прогноз в РРВ. Что значительно сокращает время получения прогнозных значений. Подобный подход к прогнозированию исследован в данной работе.

2.    Описание метода

Сглаживающие сплайны – эффективный инструмент аппроксимации зашумленных данных. Наиболее известным примером сглаживающего сплайна является кубический сглаживающий сплайн [21], хорошо изученный в режиме апостериорного сглаживания.

Регрессионные сплайны используют определенный набор базисных функций с уменьшенным количеством узлов. Реализуются они часто на основе метода наименьших квадратов. Штрафы за негладкость в регрессионных сплайнах отсутствуют.

Эффективность штрафных P-сплайнов [22] и базисных B-сплайнов [23] значительно повышается при оптимальном выборе узлов. Именно выбор узлов можно рассматривать как способ параметрической адаптации сплайна к динамике ВР [24]. Другим инструментом адаптации является оценка штрафного параметра с использованием регрессионных и вероятностных подходов [25].

Именно штрафные P-сплайны объединяют достоинства регрессионных и сглаживающих сплайнов: уменьшенное количество узлов и контроль гладкости сплайна.

В данной работе предлагается модификация P-сплайна, реализующая вариационный подход для отдельных фрагментов ВР (группы данных) [26, 27]. Объединение входных данных в группы, с одной стороны, решает проблему выбора узлов. С другой – выделяет фрагмент ВР (shapelet, паттерн) и, следовательно, реализует гибридный подход к прогнозированию на основе сходства. При этом экономичный алгоритм оценки параметров рекуррентной сплайн-функции исключает использование численных методов и тем самым позволяет реализовать сплайн в реальном времени.

Получение классического штрафного P-сплайна в апостериорном режиме основано на оптимизации специального вида функционала [24]

b

n

n

J ( S ) =α⋅ ∫ [ S ′′ ( t )]² dt + ∑ [ S ( t i ) - y ( t i )]² .            (1)

a

i =0

В (1) первое слагаемое вместе со сглаживающим параметром α определяет штраф кривизны; второе слагаемое, как и в методе наименьших квадратов, задает приближающие свойства. На основе функционала (1) возможно одновременно вычислить все звенья сплайна S ( t ), но только после получения всех измерений y ( t j ), j = 0, n, на интервале наблюдения [ a , b ].

Реализации прогноза в реальном времени потребовала модифицировать функционал (1) отдельно для каждого i -го звена сплайна, включающего группу из h входных отсчетов y ( t ⁱ _j ), j = 0, h [26]. Шаг дискретизации Δ t введен для регулирования размерности функционала

i th                            h

J ( S ) = (1 - ρ )( h Δ t )² ∫ [ S ′′ ( t )]² dt +ρ ∑ [ S ( t ⁱ j ) - y ( t ⁱ j )]². (2) i                         j =0

t ₀

Для реализации штрафного P -сплайна для i -го звена в реальном времени

S i ( τ , a i ) = a 0 i + a 1 i ⋅τ+ a 2 i ⋅τ 2 + a 3 i ⋅τ 3 ,

- q ≤τ≤ h - q ,

в [27] получены коэффициенты такой формы P -сплайна в рекуррентном виде.

a ₀ i ₌ a ₀ i -1 ₊ a ₁ i -1 ₊ a ₂ i -1 ₊ a ₃ i -1 ;

a ₁ i ₌ a ₁ i -1 ₊ 2 a ₂ i -1 ₊ 3 a ₃ i -1 ;

i ₌ ρ ( F 1 ⁱ C - F 2 ⁱ A )

• ²      BC - A ^{2   ;}

i ₌ ρ ( F 2 ⁱ B - F 1 ⁱ A )

• ³      BC - A ^{2 ;}

A = 6(1 - p ) h ⁴ + p H 5 ;

B = 4(1 -p ) h ³ + p H 4 ;

C = 12(1 -p ) h ⁵ +p H ₆ ;

F 1 ‘ = £ y ( t j ) j ² - a O H - aH 3 ;

• j =0                                                    ⁽⁴⁾

• F 2 = ^У ( t j ) j ³ - a O H - aH ;

j =0

H n = £j ⁿ , n = 2,6.

j =0

В (4) q - номер отсчета внутри i -го звена ( j = 0, h ; q = 0, h - 1 ), в котором сопряжены непрерывные производные сплайна, S^k , 1 ( t q -+11 , a ‘ ^{- 1}) ₊ = S^k ( t q , a i ) _ k =0,1 для дефекта 2 и k =0 для дефекта 1. Разрывные коэффициенты a ₂ ⁱ , a ₃ ⁱ найдены из условия минимизации функционала (2):

d J ( S ( t , a i ))_     8 J ( S ( t , a i ))_

,                                                      •

8 a [                8 a 3

Формулы (4) локальны для входных измерений внутри звена сплайна и рекуррентны относительно коэффициентов для всего сплайна.

Соотношение моментов вычисления ( t ) и сопряжения ( q ) для i -го звена сплайна порождает несколько вычислительных схем рекуррентного сплайна, подробно исследованных в [27]. Наиболее общим и приспособленным для прогнозирования ВР является текущий режим штрафного P -сплайна, рис. 2.

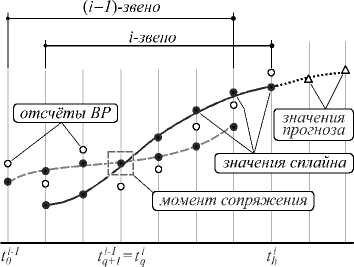
Рис. 2. Режим прогнозирования на основе штрафного P-сплайна

Модель фрагмента временного ряда в виде звена штрафного P -сплайна позволяет получать значения прогноза для т >  h в реальном времени. На рис. 2 изображен горизонт прогноза для двух значений т = h + 1 и т = h +1.

Фактически группа h отсчетов i -го звена сплайна определяет фрагмент (сегмент) ВР, объединенный общими динамическими свойствами. Поэтому выбор размера группы отсчетов h является задачей адаптации и значительно повышает качество прогнозирования.

3. Адаптация параметров штрафного P-сплайна

Одной из основных трудностей, с которыми сталкиваются исследователи при прогнозировании ВР, является поиск наилучших параметров модели прогнозирования в соответствии с заданным набором данных.

Различные методы и алгоритмы оптимизации неоднократно использовались для обучения многих структурных моделей прогнозирования, в том числе и для искусственных нейронных сетей (ИНС) [28, 29]. Это могут быть локальные техники оптимизации, классические алгоритмы глобального поиска и смешанные технологии [30]. Также разработаны эффективные методы и алгоритмы оптимизации, основанные на оригинальных идеях. Среди них и алгоритмы на базе метода оврагов И.М. Гельфанда [31], и алгоритмы на основе метода неравномерных покрытий Ю.Г. Евтушенко [32] и др. Использование классических методов оптимизации малоэффективно для многоэкстремальных функций, к которым относится большинство реальных поверхностей уровня или модельных данных в условиях помех.

Группа метаэвристических методов хорошо зарекомендовала себя при отсутствии или неполной информации о свойствах целевой функции. Получаемое без доказательства оптимальности и корректности решение (часто субоптимальное) приемлемо и с позиции вычислительных затрат. В отличие от многих классических методов поиска эвристические методы реализуют алгоритмы случайно направленного перебора [33].

Идея метаэвристических алгоритмов исходит из поведения животных или физических явлений [30]. Среди метаэвристических группа эволюционных алгоритмов успешно использована во многих научных и технических задачах. Наиболее популярное приложение эволюционных алгоритмов – оптимизация многопараметрических функций и способность одновременной манипуляции несколькими параметрами.

Для оптимизации параметров штрафного P-сплайна по аналогии с ИНС были использованы генетический алгоритм (ГА) и алгоритм искусственных иммунных систем (ИА) [34].

В ИА используется способность естественной иммунной системы вырабатывать новые типы антител и отбирать наиболее подходящие из них для взаимодействия с попавшими в организм антигенами.

ГА обеспечивает выживание сильнейших генов из множества сгенерированных на основе эволюционных принципов наследственности, изменчивости и естественного отбора [3]. Использование ГА в задачах оптимизации требует меньших вычислительных ресурсов по сравнению с ИА. Но при этом ИА допускает реализацию параллельно распределенного поиска.

Структурные схемы генетических и иммунных алгоритмов весьма схожи и схематично представлены на объединенном рис. 3.

При адаптации параметров штрафного P -сплайна использовано основное достоинство эволюционных

алгоритмов – одновременная оптимизация нескольких параметров. В данном случае были одномоментно исследованы два основных параметра P -сплайна: сглаживающий множитель ре [0,1] и длина звена h е [3,20]. Значение h = 3 соответствует использованию 4 отсчетов для построения полинома третьего порядка, а при h >20 модель сложно использовать в

системах реального времени.

Устойчивость штрафного P -сплайна подробно исследована в [35] и для выбранного текущего режима не оказывает влияния на области изменения параметров сплайна.

( Формирование начальной популяции ]

I

Генетический алгоритм

I

*

Оценка популяции

Результат: оптимальное решение

Искусственная имамунная сеть

Селекция

Отбор родителей

Клонирование родительских клеток

Скрещивание Получение потомков

Мутация родительских клеток

Мутация

Случайные изменения в генах потомков

Селекция родительских клеток и клеток мутантов

I

Обно вл ение популяции

Рис. 3. Структурная схема генетического и иммунного алгоритмов

4. Результаты вычислительного эксперимента

Оптимизация параметров штрафного P -сплайна позволила построить эффективные прогностические модели с разными горизонтами прогнозирования. Качество прогноза традиционно оценивается совокуп-

ностью показателей [1, 10, 36], отражающих временные и точностные характеристики экстраполяции.

К основному показателю точности прогноза нами были предъявлены следующие требования:

• –    независимость от шкалы ВР;

• –    устойчивость к выбросам;

• –    симметричность оценки.

И в качестве основного показателя точности прогноза известная оценка RMSE (Root Mean Squared Error) была дополнена процентным нормированием RMSPE (Percentage Error)

n

RMSPE = — £ ( y - y , . )²--00—, [%] . (5)

У n - ¹ i = 1              y max ^- y min

В формуле (5) RMSPE-мера работает с разностью между фактическим наблюдаемым значением y i и прогнозируемым значением y i .

Говоря о быстродействии алгоритма, можно оценить временную сложность алгоритма, связанную с количеством вычислений для входного массива данных. В случае Р -сплайна объем вычислений определяется формулами (4), реализуемыми в РРВ при получении очередного измерения. Алгоритм, реализующий (4), содержит единственный цикл размерности h (размер группы измерений). И в O- нотации временная сложность данного алгоритма составляет O ( h ). При этом наилучшему случаю соответствует O ( h = 3). А наихудшему – O ( h = 20). Пространственная сложность (объем памяти) также невелика и составляет (11+ h ).

Оценка прогностических свойств предлагаемого гибридного алгоритма была проведена с использованием нескольких тестовых (синтетических) и реальных ВР.

Для сопоставления точности прогноза RMSPE-ошибка была получена для случайных и оптимальных значений параметров P -сплайна. Для тестовых ВР результаты вычислительных экспериментов приведены в табл. 1.

Табл. 1. Оптимальные значения параметров и RMSPE-погрешность для тестовых ВР

CT - ,%

0%

5%

10%

15%

20%

Тест-1	,. 1П . | 2л- t ) y1 ( t ) = 10 - sin ----- I 100 J
h opt ρ opt RMSPE min	ГА 3 0,99 0,006	ИА 3 0,99 0,006	ГА 8 0,61 0,69	ИА 5 0,72 0,65	ГА 3 0,49 1,17	ИА 4 0,68 1,18	ГА 3 0,42 1,66	ИА 4 0,37 1,58	ГА 3 0,35 2,01	ИА 4 0,3 2,06
Тест-2				y 2 ( t ) = sin		^ t 1- e 002-t + 3 . 20 J
h opt ρ opt RMSPE min	ГА 3 0,99 0,025	ИА 4 0,99 0,025	ГА 12 0,97 1,4	ИА 11 0,83 1,32	ГА 3 0,62 2,38	ИА 3 0,58 2,47	ГА 3 0,54 3,39	ИА 3 0,48 3,25	ГА 3 0,45 4	ИА 3 0,43 3,84

Оптимальные значения параметров гибридного алгоритма прогнозирования h opt и ρ opt найдены на основе эволюционных алгоритмов. Характерно, что ГА и ИА приводят к близким, но все же различным значениям оптимальных параметров. Но при этом RMSPE-погрешность примерно одинакова при заданных значениях уровня шума входных данных σ ξ . В качестве шума был выбран случайный сигнал ξ ( t ): M { ξ ( t )} = 0; M { ξ ²( t )} = σ ² ξ .

Основная цель исследования прогноза на тестовых данных – оценка трендовой составляющей ВР в условиях шума. Графический анализ минимальных значений погрешности, приведенный на рис. 4 а, б , показывает значительное сокращение шума входных данных при горизонте прогнозирования на 1 шаг вперед. Погрешность входных данных в среднем уменьшается в 5 –10 раз в зависимости от вида тестовой функции. В плане вычислительной сложности используемые алгоритмы оптимизации не имеют преимущества друг перед другом.

Сравнивая производительность ГА и ИА, следует отметить, что время работы иммунного алгоритма значительно выше, чем генетического, в среднем в 1,5–1,75 раз. Поэтому для настройки параметров штрафного P-сплайна для реальных данных использован ГА.

В качестве реальных ВР были использованы данные о цене закрытия акций компаний ПАО «Мегафон» и АО «Сбербанк России» в 2018–2019 гг. Для отображения результатов исследования использованы диаграммы размаха, представленные на рис. 5 а, б . А соответствующие выбранным параметрам значения погрешности прогноза приведены в табл. 2.

Табл. 2. RMSPE-погрешность для реальных временных рядов

Акции ПАО «Мегафон»
Параметры P -сплайна	h =5; ρ =0,2	h =5; ρ =0,5	h = 10; ρ =0,5		h = 10; ρ =0,9	h =15; ρ =0,5	h opt =4; ρ opt =0,87
RMSPE, %	7,164	5,564	6,450		5,318	7,535	3,643
Акции АО «Сбербанк России»
Параметры P -сплайна	h =5; ρ =0,2	h =5; ρ =0,9	h = 10; ρ =0,6		h =15; ρ =0,9	h =15; ρ =0,2	h opt =7; ρ opt =0,91
MSPE, %	5,210	3,151	3,558		4,843	6,231	3,151
Графическое сопоставление реальных временных рядов и соответствующих прогнозных моделей, рис. 6, выявило ряд дополнительных свойств P -сплайна в составе гибридной модели прогнозирования. Исходя из RMSPE-оценки качество прогнозиро-				вания на основе штрафного сплайна находится в пределах 3–4%. Это является неплохим показателем в сравнении с известными методами прогнозирования, детально исследованными в [10].

Цена акций, тыс.руб.

1601----------------------------------------------------------------------------------------------------

. 401.10      01.11      01.12   „ 01.01       01.02       01.03 ..   01,04       01.05       01.06   ,

а)   I------------ 2018------------^л--------------------------------2019--------------------------------'

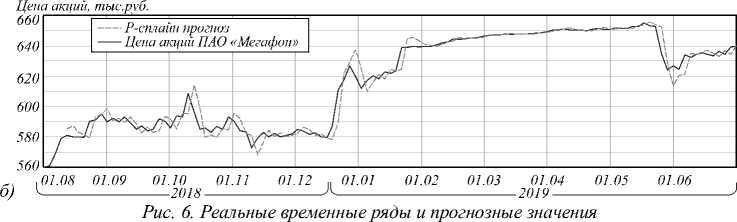
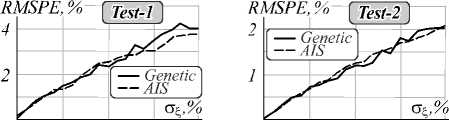
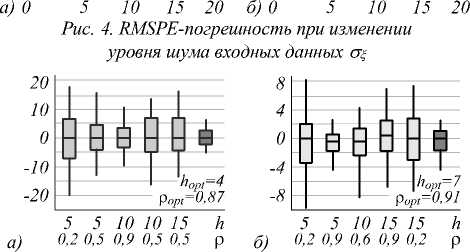
Рис. 5. Разброс RMSPE-погрешности для произвольных и оптимальных значений параметров P-сплайна

В исследовании [10] одиннадцать наиболее известных алгоритмов прогнозирования сопоставлены по трем показателям: MSE-погрешность, TU-коэффициент Тейла, отражающий предсказательные возможности алгоритма по отношению к наивной модели прогнозирования, и POCID-показатель сохранения тенденций.

Сравнение предлагаемого алгоритма на основе P -сплайна с исследуемыми в [10] методами было проведено на одинаковых наборах тестовых данных, включающих 17 детерминированных, 15 случайных и 8 хаотических ВР из репозитария [37].

Полученные в ходе исследования MSE-погрешности для всех двенадцати алгоритмов прогнозирования находятся в широком диапазоне [10-9 – 109]. Поэтому для наглядного отображения результатов на рис. 7 приведены средние значения MSE в логарифмической шкале для каждой группы ВР. Можно отметить, что минимальная MSE-погрешность для алгоритма SARIMA близка к нулю и на рис. 7 находится в отрицательной плоскости.

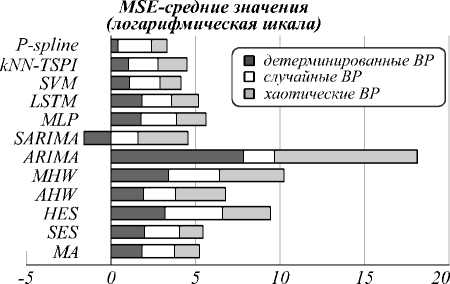
Рис. 7. Диаграмма средних значений MSE-погрешности

TU-коэффициент отражает эффективность алгоритма в сравнении с тривиальным повторением предыдущих значений ВР (наивная модель прогнозирования). В [10] использована следующая интерпретация этого коэффициента: если TU= 1, то эффективность алгоритма такая же, как у наивного алгоритма; TU> 1 – эффективность ниже; TU< 1– выше; а при TU ≤ 0,55 алгоритм способен качественно выполнять прогноз. И для 17 детерминированных ВР на рис. 8 приведены соответствующие значения TU в каждом из трех указанных диапазонов.

Весьма важным при прогнозировании ВР является сохранение тенденции процесса. Значение показателя POCID изменяется от 0 до 100: 100 – полное совпадение, 0 – отсутствие совпадения тенденции исходного и прогнозируемого ВР. И для всех типов детерминированных ВР показатели POCID приведены для исследуемых двенадцати алгоритмов прогнозирования.

Процентный POCID-параметр довольно нагляден для отображения тенденции. И в зависимости от прикладной задачи может быть установлено его пороговое значение.

Что касается предлагаемого в данной работе алгоритма прогнозирования на базе Р -сплайна, то следует отметить его эффективность по MSE- и TU-показателям и более низкую эффективность в плане показателя тенденций POCID.

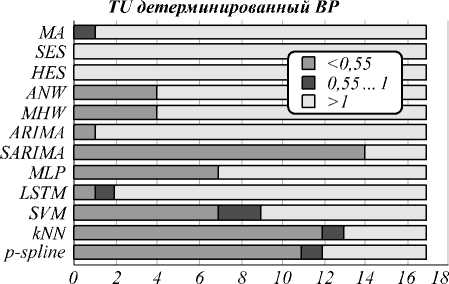
Рис. 8. Диаграмма распределения TU-коэффициента по диапазонам

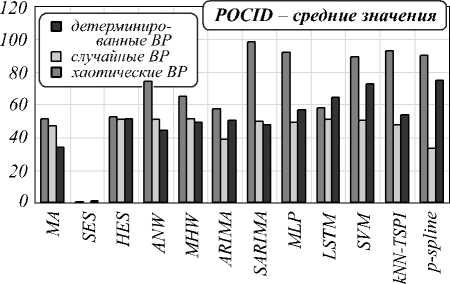
Рис. 9. Диаграмма средних значений POCID-параметра

Что касается гибридных методов оптимизации, то можно указать весьма эффективные комбинации. Например, комбинация нейронные сети и регрессионные методы (ARIMA) дает ошибку прогноза около 1 % [38]. А гибридный метод на основе kNN при использовании многомерных временных рядов имеет ошибку прогноза менее 1 % [1]. Однако в последнем исследовании [1] глубина предыстории составляет 49900 точек ВР. А прогноз осуществляется на 1 шаг вперед по последним 100 точкам данных ВР. Подобный подход к прогнозированию делает его невозможным в масштабе реального времени. Предлагаемый нами гибридный метод, основанный на штрафных P -сплайнах, обеспечивает приемлемое соотношение качества прогнозирования и скорости прогнозирования. При этом тип и природа входных данных не анализируется и не требует предварительной обработки.

Заключение

В данной работе рассмотрен гибридный подход к прогнозированию ВР, воспроизводящий динамику процесса в форме рекуррентной модели штрафного P -сплайна.

Предложенная модель была протестирована на ВР-стоимости акций нескольких известных компаний. Сопоставление с результатами других гибридных методов (на основе ИНС и kNN-классификатора) показало, что точность прогноза предложенного метода хотя и несколько ниже (в среднем в 2 раза), но вполне допустима для использования в инженерных приложениях. Полученные исследования позволили сделать заключение, что для получения эффективных прогнозов необходимо производить адаптацию параметров модели. При использовании для адаптации генетического и иммунного алгоритмов оптимизации предпочтение отдано генетическому, скорость прогноза с его использованием в среднем выше в 1,5 раза при сопоставимой точности.

Также необходимо отметить важное свойство предлагаемой модели прогнозирования – малая глубина предыстории (порядка 10 точек ВР). А это вносит основной вклад в скорость прогноза и делает данную модель пригодной для использования в реальном времени.

Работа выполнена при поддержке гранта РФФИ (№ 18-07-01007).