Гидродинамический начальный участок в плоском пористом канале при напорном изотермическом ламинарном течении ньютоновской среды

Классическая физическая модель пористых сред представляется как плотная упаковка сфер [1], пустоты которой соединены между собой и полностью заполнены жидкостью без фазовых переходов, что, как правило, соответствует неподвижным зернистым слоям в различных технологических аппаратах [2]. Численным интегрированием уравнения макроскопического пограничного слоя, полученным из модели Дарси – Бринкмана – Форчхеймера стандартным интегральным методом, в предположении конечной его толщины, было показано, что длина гидродинамического начального участка в неподвижном зернистом слое сопоставима с размером частиц или пор [3]. Это давало основание, наряду с эффектом выравнивания пористым слоем скорости потока в поперечном сечении канала [4], обосновывать применение режима идеального вытеснения для моделирования явлений переноса в зернистых слоях [5,6]. Однако появление новых технологий получения пористых материалов из вспененных металлов, графитов, керамики и полимеров с высокими значениями пористости и проницаемости [7] и использование их для интенсификации различных процессов [8] вновь инициировало проблему идентификации гидродинамического начального участка и его влияния на тепломассообмен [9].

В [10], по-видимому, впервые анализировалось влияние поперечной неоднородности поля скоростей на теплообмен при ламинарном течении ньютоновской жидкости в высокопроницаемом канале, но опять-таки в приближении малости начального гидродинамического участка и с введением ограничения на использование предложенной модели (по типу модели Дарси – Бринкмана) в виде критерия h ε/K > 200, где h – высота канала, м; ε – пористость; K – проницаемость, м2 . Численное исследование уравнения Дарси – Бринкмана в формате 3-D, в предположении параболической зависимости аксиального давления, позволило установить длину начального гидродинамического участка в высокопроницаемом (число Дарси Da = 5 · 10-5) канале квадратного сечения L = 0, 05 Re (число Рейнольдса определялось по расходу среды через проходное сечение канала) [11], однако обобщения полученных результатов для широкого спектра изменения числа Дарси не было сделано.

Из условия стабилизации толщины макроскопического пограничного слоя в [12] при равенстве нулю фактора Форчхеймера показано, что в плоском канале с изотропным пористым наполнителем и с проницаемостью, подчиняющейся закону Козени – Кармана, длина ламинарного начального гидродинамического участка пропорциональна числу Рейнольдса, а коэффициент пропорциональности есть функция проницаемости. Такой подход был использован при определении входного участка для анизотропной среды, заполняющей цилиндрический канал [13].

До настоящего времени экспериментального подтверждения корректности полученных данных и возможности их экстраполяции на высокопроницаемые среды, кроме указанных теоретических оценок и результатов вычислительного анализа, пока нет. Поэтому необходимым является развитие альтернативных подходов (например, основывающихся на предположении об однонаправленном течении ньютоновской среды в пористом канале [14]), с помощью которых возможно на основе сравнительного анализа сделать выводы о точности имеющейся информации о длине начального гидродинамического участка.

1. Постановка задачи

Рассматривается установившееся изотермическое напорное течение ньютоновской жидкости в горизонтальном плоском анизотропном пористом канале полубесконеч- ной длины в декартовой системе координат формата 2-D (x, y – продольная и поперечная координаты) с началом на нижней стенке (рис. 1).

Будем идентифицировать ламинарный режим по числу Рейнольдса, определение которого следует из модифицированного уравнения Эргуна [15]

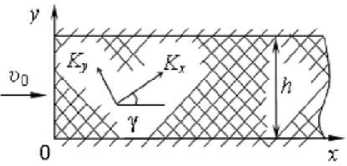
Рис. 1. Расчетная схема: υ 0 = const – скорость жидкости на входе в канал; K y , K x – проницаемости пористой среды; угол ориентации γ

2k V      υ 0 d p ρ f

= ·

3 (1 - ε)    µf со значением меньше 50, где kV – коэффициент формы характерных элементов размера dp пористой матрицы; ρf , µf – плотность и динамическая вязкость жидкости.

Так как для установившегося ламинарно- го режима течения инерционные эффекты незначимы [16], то уравнения неразрывности и Дарси – Бринкмана – Форчхеймера переходят в стационарную систему Дарси

– Бринкмана [17]:

V- и = 0;                                    (1)

⁽ r^V ) ^U = p f ( ^-V P ⁺ т ^V 2 ^{U -} K °)-               ⁽²⁾

где U - вектор скорости жидкости; p - давление; K - тензор проницаемости пористой матрицы, представленный в инвариантной записи [18]:

K =

K x cos ² y + K y sin ² y (K x — K y ) cos y sin y (K x — K y ) cos y sin y K x sin ² y + K y cos ² y

В компонентом виде система (1), (2) с учетом того, что

K „ 1

где K „1 = K_T ¹ cos ² y + K „ ¹ sin ² y ; K „1 xx        x               y             xy

K - ¹ sin ² y + K „ 1 cos ² y , такова: xy

- 1 xx

- 1 yx

- 1 xy ^K y ^- y ¹

- 1

yx         x

- 1

-

K y¹)^cos y ^sin y ; ^K yy =

∂υ

∂υ ∂υ

—- + —= 0;

∂x ∂y

¹ U^x x^Tx + U y ε ∂x

dvA = ∂y

ε ∂p ρ f ∂x

µ f ∂ ² υ x

ρ f ∂x ²

+

∂ ² υ x ∂y ²

-

-E^ f K xx^x + ^K yy1 ^U y ) ' ρ f

¹ fu , d^u y +u y d^u y) = ε ∂x ∂y

ε ∂p ρ f ∂y

, ^ f ( ^{d 2 U} y

ρ f ∂x ²

+

∂ ² υ y ∂y ²

-

^— °p f ^K yx1 ^U x ^{+ K} yy ^U y ^ '

где U x , U y - компоненты u . С помощью стандартного приближения макроскопического пограничного слоя [12] уравнения (5) и (6) трансформированы:

1 / dU _x      dU_x\      ° dp   p f d²U x

^U x      + ^U y       =1

ε     ∂x      ∂y       ρ f ∂x   ρ f ∂y ²

-

^µ f - 1

°     ^lvx x ^U x ;

ρ f

∂p ay

Как и в [19], учтем в левой части (7) квадратичные члены частично, следуя методу Озеена, тогда

υ 0 ∂υ x ε ∂x

^dp + ^ f d ² U x ρ f ∂x ρ f ∂y ²

-

ε^{µ f} K _x ^- _x ¹ υ x , ρ f

где υ ₀ – скорость на границе пограничного слоя. Система уравнений (4), (8) и (9) с начальными

U y (0, y ) = 0, U x (0, y) = U o = const

(условия ≪прилипания≫ на стенке (10) также выполняются и для υy) представлена в безразмерной форме: ∂VX ∂VY dX 1 dY = ’                                ( ) ∂P dY=0i                                (12) dVx     ddP   e d2Vx   e 2 dX = -E dX + Re dY2 - Req Vx;                (13) Vx (0’Y) = 1;                                (14) Vx (X, 0) = Vx (X, 1) = 0,                          (15) и граничными условиями

U x (x, 0) = U x (x, h) = 0

с помощью относительных переменных: X = x/h ; Y = y/h ; V x,y = U _x,_y /u q ; P = p/ (P f U q ) ; Re = u ₀ hp f / p f - число Рейнольдса; Da = K x /h ² — число Дарси; A = cos ² y + П sin ² Y; П = K x /K y ; q = V eA/Da. Система (11) - (15) дополнена условием сохранения расхода жидкости в любом сечении канала

I V x (X,Y) dY = 1. 0

2. Решение

Из осреднения уравнения (13) по поперечному сечению канала, принимая во внимание условие (16) и учитывая симметрию касательных напряжений потока жидкости на стенках, следует, что dP _ 2 /dVx\       q2

dX = e • Re VF) Y=1 — e • Re’ поэтому уравнение (13) вместе с краевыми условиями (14) и (15), после подстановки в него (17) и последующего применения полуограниченного интегрального преобразования Лапласа [20] по переменной X, сводится к краевой задаче отыскания изображения скорости VXL (s, Y) с комплексным параметром s:

d ² V X ^{L) ( s,Y})     f 2, ^Re • s At /L )/ _v ,    Vd' XL ⁽ s’ 1)   q ^{2    Re}.

dY ^{2          +} VV ^(s,Y ) = ²FY         ^- ’

VXL) (s, 0) = VXL) (s, 1) = 0, решение которой, согласно [21] есть

V ( L ) D n - C       1 + sh ^[ B (s) ^Y ] + sh [B (s) (1 - ^Y )] I

VX (s,Y)-C(s)|-1+           shB(s)           J’ где

C (s) = 2

dv X^{L )} (s, 1) dY

- q- - Re /B 2 (s), sε

B (s) = Уq 2 .Re ' s

После дифференцирования (18) по Y найдено dvXL (s,Y)

dX

- IB (s)

^ch B (s) - ¹ 1 //i - ² sh B (s)    / [     B (s)

'ch B (s) - 11) (srj

sh B

тогда

C _{( s )} = - 1/1 - 2   [ ch В (s) - 1 1)

s ( B (s)     sh B (s) J J и (18) записано в виде

• (L)        ₌ B (s) ^{{ sh} B (s) ^- sh [B ^{( s )} Y ^] + sh [B ^{( s ) (1 -} Y ^{)] }}

V ^{х ( s,}Y )             s { B (s)sh B (s) - 2 [ch B (s) - 1] }

Числитель и знаменатель соотношения (19) представляют собой бесконечные полиномы целой степени s , причем порядок полинома знаменателя превышает порядок числителя, так что выполнены условия второй теоремы Хэвисайда обращения изображения по Лапласу [20], применение которой к (19) приводит к решению системы

• (11)    – (15):

V x (X, Y ) = q { sh q - sh (qY ) - sh [q (1 - Y )] } / / [q sh q - 2 (ch q - 1)] -

∞

- 2^2 M n {- sinM n + sin (M n Y ) + sin [M n (1 - Y )] } x n=1

x exp

/ (M n ⁺ q ² ) y°^s M n где µ n – корни уравнения

ife (M n +q) xJ

-

1 •

--- sin M n , µ n

M n sin M n = 2(1 - cos M n ), n = 1, w ,

причем корню m = 0 соответствует нулевое слагаемое в решении (20). Из (11) и (17) с использованием (20) получено:

, x     2f

V y (X, Y ) = — \ M n <  sin M n Y

Re\ n=1'

--{cos [M n (1 - Y )] µ _n

-

-

• exp

P - P o =

— [1 - cos (M n Y)] - µ _n

cos M n

) X]/6

-|- (q 2 (1 - ch q) X   [q sh fRe

lie ( м п +q ²

cos M _n

-

q

-

}1

1 •      1

— sin M n ;

µ n

• 2    (ch q - 1)] +

∞

+2 ^ м П (1 - M n cos M n ) {1 - exp n=1

t [i^fe (м П ⁺ q ² )] [(м П ⁺ q ² ) (^cos M-

• ^{1    -} Re <^M n ⁺ .П - M- sin M n

-

AX

ReDa ’

где P q = p o / (p f и 2 ), p ₀ - давление на входе в канал.

3. Анализ

Если в канале отсутствует пористая матрица, то соотношение для аксиальной скорости (20) в пределе при г ^ 1 и Da ^ то таково

V x (X, Y) = 6Y (1 - Y ) - - 2^ {- sin Ц п + sin (ц п Y ) + + sin Ц (1 - Y )] } exp ( - ц ^ Х/Re) / ( - sin Ц п + Ц п cos Ц п ).

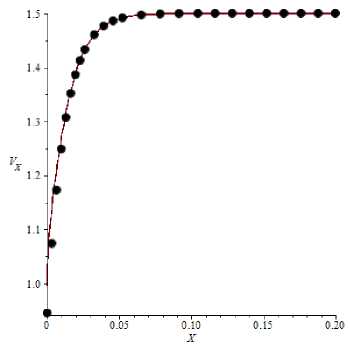
Рис. 2. Изменение продольной скорости V x при Y = 0, 5 и Re = 1 с различным числом членов ряда в (24):-- 100; • - 1

Расчеты показывают (рис. 2), что для оценки максимальной аксиальной скорости течения вполне достаточно ограничиться в (24) первым ненулевым членом ряда при Y = 1/2

V x (X, 1/2) « 2

где Ц 2 ~ 8, 987. Из условия

-

2 [ - sin Ц 2 + 2 sin (Ц 2 /2)]

- sin Ц 2 + Ц 2 cos Ц 2

^exp (" Re X) ■

V x (X, 1/2) =0, 99V x ( то , 1/2)

найдено

L = 0,178Re L

где относительная длина начального гидродинамического участка L и число Re L рассчитаны по геометрическому масштабу h/2. Соотношение (25) коррелирует с результатами [19, 22] для напорного течения ньютоновской жидкости в плоском горизонтальном канале.

Расчетами по соотношению (20) установлено, что порозность вблизи входного сечения влияет в меньшей степени на структуру поля аксиальной скорости в отличие от проницаемости, определяемой комплексом q , который также характеризует и строение пористой матрицы ( K x = K y - структура изотропна при любом угле ориентации Y (A = 1); K x = K y — структура анизотропна, причем направление наибольшей проницаемости также зависит и от y )• Для A = 1 увеличение проницаемости приводит

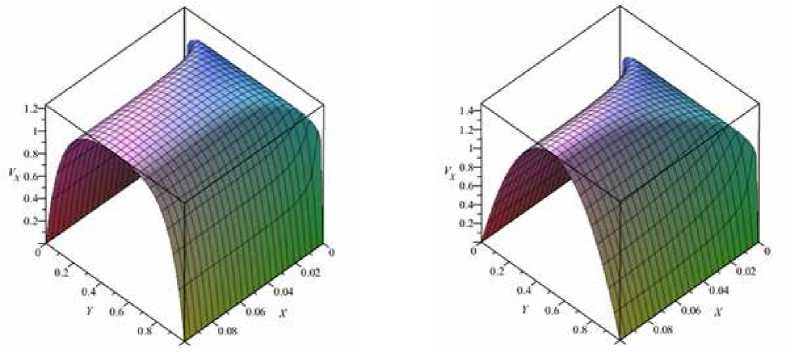
aб

Рис. 3. Поле аксиальной скорости при A = 1, Re = 1, г = 0,4 и различных q : a -0,01: б – 10,0

к возрастанию длины начального гидродинамического участка (рис. 3), причем при q = 0, 01 структура аксиальной скорости характерна для высокопроницаемой пористой матрицы, а при q = 10 - плотному зернистому слою, что подтверждают профили давления вдоль канала (рис. 4).

Влияние поперечной скорости на структуру течения невелика даже для высокопроницаемой пористой матрицы, о чем свидетельствует незначительное искривление линий тока вблизи входа в канал (рис. 5).

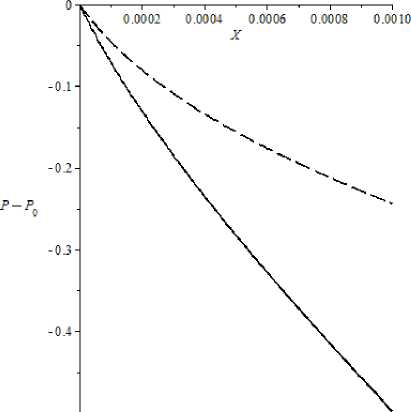
Рис. 4. Изменение давления в аксиальном направлении пористого плоского канала при A = 1, Re = 1, г = 0,4 и различных q :   0,01; 10,0

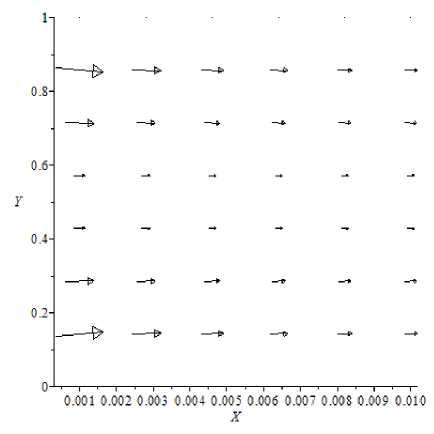
Рис. 5. Линии тока поля скоростей в области, прилегающей ко входу в канал при A = 1, Re = 1, г = 0,4, q = 0, 01

Рис. 6 иллюстрирует возможность достаточно точного представления аксиальной скорости в плоском пористом канале при Y = 1/2 и различных значений q приближением решения (22), в котором учтен только первый ненулевой член ряда.

Из такого приближения решения (22) в виде

V x (X, 1/2)

q [sh q — 2sh (q/2)]

q sh q — 2 (ch q — 1)

2^ 2 p 2 + q ²

[ — sin ^ 2 + 2 sin (^ 2 /2)]

--------------------exp cos ^2 - sin ^2/^2

Re «+q 2 > x

получено соотношение для длины гидродинамического начального участка, аналогичное (25)

L = b (q)Re L ,

где

b ( q ) =

1               q[sh q -2sh (q/2)]

E (p 2 + q ² )   P 0 q sh q - 2 (ch q — 1)

(p 2 + q ² ) (cosP 2 — sin P 2 /P 2 ) 2^ 2 [ — sin P 2 + 2 sin (p- 2 /2)]

. (26)

Таким образом подтверждена линейная зависимость длины гидродинамического начального участка от числа Рейнольдса для плоского пористого канала при ламинарном режиме течения ньютоновской жидкости как для изотропных, так и анизотропных сред, а коэффициент пропорциональности коррелирует с данными из [13] (рис. 7).

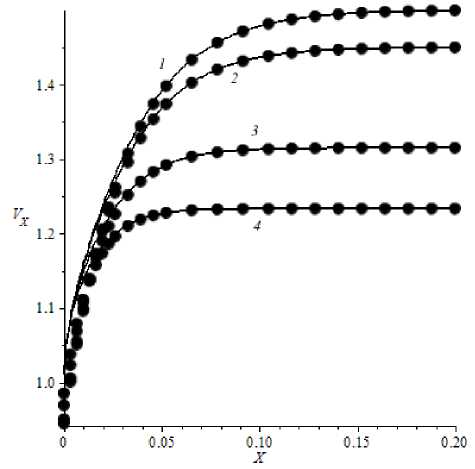
Рис. 6. Аксиальная скорость в плоском пористом канале при Y = 1/2; e = 0,4, A = 1, Re = 1, различных q: 1 - 0,01; 2 - 3,0; 3 – 7,0; 4 – 10,0 и с числом членов ряда в решении: — – 100; • – 1

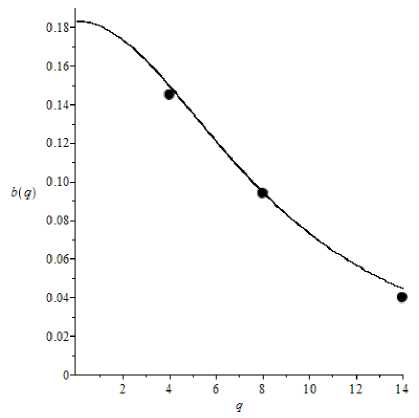
Рис. 7. Зависимость b (q) при e = 0,4 и A = 1 :-- расчет по формуле (27); • – данные [13]

Заключение

Показана возможность аналитического решения задачи о ламинарном начальном гидродинамическом участке в горизонтальном пористом плоском канале изотропной и анизотропной структуры без использования понятия толщины пограничного слоя и дополнительной информации о профиле скорости по его толщине. Качественная и количественная адекватность полученных полей скорости и давления позволяют применять такой подход для решения аналогичных задач в пористых каналах с по-перчными сечениями других геометрий.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-38-90114.