Гидродинамическое моделирование процесса формования хлебопекарного теста и кондитерских масс

Важнейшей задачей хлебопекарной и кондитерской отрасли является расширение ассортимента и повышение качества выпускаемой готовой продукции [1–3].

Непрерывное увеличение темпов роста выпускаемой продукции с одновременным улучшением ее качества в объектах хлебопекарного и кондитерского производства связывается с повышением биологической ценности и вкусовых достоинств хлебобулочных, макаронных и кондитерских изделий [4–10].

Тестовый материал является дисперсной системой, течение которой под нагрузкой зависит от ее физико–химических особенностей: от расположения и формы молекул, температуры, влажности, а также концентрации, которая определяет вязкость и характер течения. В работах [4–6, 8] показано влияние на структуру дрожжевого теста солодового препарата, внесение которого снижает упругие свойства теста, увеличивая пластичность. Также установлено влияние дозировки кукурузного масла и семян льна на качественные показатели хлебобулочных изделий. Установлена взаимосвязь показателей качества муки и реологических свойств полученного из нее теста, а также качество хлеба [11–14].

Оценочные показатели для прогноза качества хлебобулочных и кондитерских изделий определяются, главным образом, реологическими свойствами теста [15–18]. Показано, что значение реологических свойств теста помогает заранее определить усилия в процессе формования теста и ее способность сохранять форму, выбрать оптимальный технологический режим, обеспечивающий высокое качество готовой продукции.

Одним из основных средств достижения целей улучшения качества и расширения ассортимента кондитерских и хлебобулочных изделий является повышение эффективности научных исследований, совершенствование форм связи науки с производством. С этой целью используют методы математического моделирования реологических свойств тестовых заготовок в условиях напряженно-деформированного состояния, позволяющие связать между собой в виде математических зависимостей нагрузку, деформации и скорости деформирования. Представлен [19] вывод реологического уравнения деформирования сахарного теста в условиях одноосного сжатия, и реализации его в процессах формования заготовок сахарного печенья. Исследуется деформационное поведение упруго-вязкопластичной среды в испытаниях на ползучесть. Установлены границы значений силовых воздействий при реализации процессов формования тестовых заготовок сахарного теста, обладающих свойствами вязкопластичности.

Разработана математическая модель процесса прессования кондитерской массы на прессе глубокого отжима [20].

Полученные в работе квадратичные зависимости адекватно описывают реализуемый процесс прессования и позволяют объективно оценивать работу пресса глубокого отжима, а также минимизировать себестоимость готовой продукции.

Для снижения вязкости кондитерской массы предложено использовать крахмальную патоку [21] при прямом отжиме в технологии производства овощной пасты. Это дает возможность создавать предпосылки для лучших условий последущих технологий. Многообразие теоретических подходов к описанию реологических свойств и перечисленные математические модели, описывающие поведение исследуемых сред в условиях напряженно-деформированного состояния, показывают важность взаимосвязи реологических и кинематических характеристик в условиях квазистатических испытаний. Достаточно подробную картину изменения реологических свойств материала можно получить, исследуя кривые ползучести тестовых заготовок. Однако, несмотря на значительное количество работ и разнообразных подходов к процессу формования структурированных дисперсных систем, к которым относятся хлебопекарное тесто и кондитерские массы, пока нет удовлетворительной теории, связывающей реологические свойства исследуемой среды с параметрами их структуры. Нет удовлетворительной методики определения реологических констант аномальных жидкостей [22], используемых, зачастую, в качестве модельной среды при описании напряженно-деформированного состояния хлебопекарного теста и кондитерских масс.

Цель работы и постановка задачи

Целью предлагаемого исследования являются гидродинамическое моделирования процесса деформации в условиях формования (плоского прессования) тестовых заготовок, а также, в рамках этой модели, показать возможность экспериментального определения реологических параметров модельной среды: коэффициента консистенции (густоты) и показателя вязкости.

В основу реализации проблемы плоского прессования хлебопекарного теста положена задача нестационарного, осесимметричного сдавливания нелинейно-вязкой среды, находящейся в пространстве между двумя сближающимися между собой параллельными дисками.

К настоящему времени известны опубликованные работы с подобной постановкой задачи [23–25]. Исследуется точное решение уравнений Навье–Стокса в деформируемом слое ньютоновской жидкости между параллельными пластинами, расстояние между которыми изменяется по степенному закону [23]. Решаются задачи плоского деформированного состояния при прессовании композиционных материалов, когда в качестве модельной среды используется идеально пластическое тело [24] и ньютоновская жидкость [25].

Решение задачи

Рассмотрим задачу о нестационарном, осесимметричном течении нелинейно-вязкой, изотропной, несжимаемой среды, сжимаемой постоянной силой сближающимися параллельными, абсолютно жесткими дисками радиусами R . При этом вещество в пространстве между сближающимися дисками в силу своей изотропности и несжимаемости выдавливается равномерно во все стороны по плоскости диска, образуя плоский слой радиусом r ( t ) < R и независящей от радиуса толщиной H ( t ) в каждый момент времени t (рисунок 1).

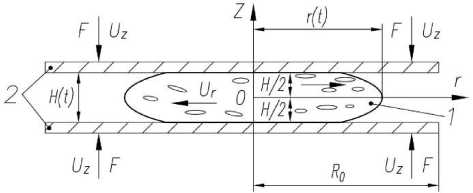
Рисунок 1. Принципиальная схема плоского формования (прессования) тестовой заготовки 1 толщиной H (t) и радиуса r (t) в момент времени t , находящейся в условиях сжатия постоянной силой F сближающимися между собой со скоростью Uz (t) параллельными, абсолютно

Для описания вязкого осесимметричного сдавливания тестовой заготовки в качестве модельной среды используем аномальную жидкость, соответствующую по вязким параметрам свойствам реального вещества, а ее закон течения – уравнению Освальда де Виля [27], согласно которому взаимосвязь между сдвиговыми напряжением т и скоростью деформации у определяется степенной функцией

т = Ц-у",                 (1)

где коэффициент консистенции ц и показатель вязкости n – параметры, зависящие от структуры вещества. Предположим далее, что исследуемая среда, занимающая пространство между сближающимися со скоростью U_z =- dH ( t)/dt дисками, представляется собой в каждый момент времени t цилиндрический слой толщиной H ( t ) и радиусом r ( t ) . Условие несжимаемости такого слоя служит постоянство его объема V :

V = n r ² H = const .          (2)

С условием несжимаемости (2) связана зависимость между скоростью сближения деформирующих плоскостей U и радиальной скоростью U в произвольно выбранном окружном сечении r = r ( t ) . Эта зависимость представляет собой уравнение неразрывности среды:

H 2

nr²U_z = 2nr j U_r ( z ) dz .        (3)

• - H / 2

Радиальная скорость U характеризует скорость растекания деформируемой среды по площади поверхности сближающихся плоскостей.

Представим закон вязкого течения (1) в обозначениях, соответствующих рисунок 1:

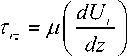
Figure 1. Schematic diagram of flat forming (pressing) of a test piece 1 with a thickness H ( t ) and a radius r ( t ) at time t , located under compression conditions with a constant force F approaching each other at a speed U_z ( t ) by parallel, absolutely hard disks 2 radii R >  r max = R in the coordinate system ( r , z ).

Учитывая линейную зависимость между касательными напряжениями и радиальным градиентом давления [23, 25]

^T rz

dP dr ^,

Предлагаемая схема деформирования, по существу, реализуется в устройстве «тесто-пресс» (пресс холодной формовки заготовок для пиццы, лапши, коржей различного типа для образования плоской лепешки) [26].

из условия (4) получим дифференциальное уравнение разделяющимися переменными в предположении, что градиент давления dP dr не меняется по толщине сжимаемого слоя:

dUr

( 1 dP \

— •-- v ц dr J

- z^s - dz ,

где s = 1/ n .

Интегрирование обоих частей (6), с учетом идеального прилипания вещества с поверхностями плоскостей [ U _r ( ± H /2 ) = 0 ^ , приводит к распределению радиальной скорости течения среды по толщине слоя:

сближения деформируемых дисков в любой момент времени t с заменой R = (VoJnH)12:

Uz (t )=

z             \ о              5 +1

( n + 3 ) ⁵ F n "2"

7 ^{5         (} 3 ^{+ 12} 5 )

Z, ^д 0 ₀

⁵ ( 1 + 5 )

- H ²

H ^{+ 1}    dP

•

( 5 +1)- д5   dr

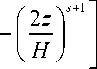
Видно, что множитель, стоящий в квадратных скобках (10), является константой A :

Видно, что максимальные значения U лежат в плоскости z = 0.

В целях исследования распределения давления прессования в радиальном направлении деформируемого слоя необходимо подставить значение радиальной скорости (7) в условие неразрывности (3) и полученное после этого выражение дважды проинтегрировать: сначала по z , чтобы получить значение радиального градиента давления dP dr , а затем по радиусу r – для распределения давления вдоль радиуса. Получим в итоге

(n + 3У F⁵n ²

A = -------'  ,------ ,

(2д) VV^

поэтому выражение (10), с учетом (11), можно прологарифмировать:

1g U . = 1g A + 5 ( 1 + 5 ) 1g H .      (12)

Дифференцируя обе части (12), получим:

d (lg U.) = 5 f1 +1). d (lg H)  2 ( n J

P ( r ) = P ( R ) +

( 2 + 5 ) n U n R n ^{+ 1} д 2 n ( n + 1 ) H^{2 n + 1}

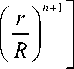
Здесь R – максимальный радиус тестового слоя (лепешки).

Подставляя в уравнение (8) вместо P его значение P = dF/d m , в предположении P ( R ) = 0, получим уравнения для элементарного усилия формования

_dF = д ( ² + 5 ) n U n R n ^{+ 1} 2 ⁿ ( n + 1 ) H^{2 n + 1}

1 -

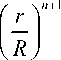
d m .

Равенство (13) означает тот факт, что в процессе формования зависимость между скоростью сближения дисков и толщиной деформируемого слоя H в двойных логарифмических координатах ( lg U_z - lg H ) должна быть линейной с наклоном прямой линии, зависящим только от показателя вязкости n . Определив на некотором участке деформирования приращения A ( lg H ) и A ( lg U_z ) , и заменив ими дифференциалы в (13), получим уравнения для экспериментального определения n :

n =-----;-------;-----.

2 A ( lg U_z )/ A ( lg H ) - 5

Интегрируя обе части последнего выражения по плоской круговой поверхности d m = 2 n rdr , получим значение суммарного усилия F , действующего на формуемую среду со стороны сближающихся дисков

_{F =} пд( 2 + 5 ) n U n R n ^{+ 3} 2 n ( n + 3 ) H¹⁺² n

.

Следует заметить, что выражения (8) и (9) при n = 1 совпадают с полученными в работе [23] для ньютоновской жидкости.

Соотношения (7)–(9) не только определяют динамику течения среды между сближающимися дисками, но и позволяют в рамках одного испытания определить значения реологических характеристик, входящих в уравнение течения модельной среды.

Действительно, учитывая условия постоянства объема деформируемой среды (условия несжимаемости) V = n R ² H = con5t, из формулы (9) можно получить значение скорости

Для определения коэффициента консистенции д опять воспользуемся соотношением (9), условием неразрывности и значением скорости сближения параллельных плоскостей. Из формулы (9) получим дифференциальное уравнение с разделяющимися переменными:

dH     2 F^n п²” (n + 3) ”n

——- =------ ^dt

H ³<¹⁺'¹” )      д ¹ ” ( 2 n + 1 ) V²”

интегрирование которого приведет к выражению для определения коэффициента консистенции д :

F ( tn ) ” 2 ” ^{- 1} n ” + ¹ ( 13 n + 15 ) H²⁺^ n ( 2 ” + 1 ) ” V o ” + 3

Значения (14) и (16) показывают, что оба параметра ( д и n ) закона течения (1) могут определяться из одного опыта по экспериментальной зависимости толщины деформируемого слоя от времени.

Следует отметить, что в расчетные формулы (14) и (16) входят мгновенные значения скорости сближения плоскостей, толщины деформированного слоя среды и их приращения, поэтому даже сравнительно малые ошибки в оценке толщины слоя приведет к значительным погрешностям значений искомых параметров.

Дифференциальное уравнение (15) позволяет получить зависимость от времени толщины тестовых заготовок, или время, затрачиваемое на уменьшение толщины деформируемой прослойки от H до H , что позволяет, в той или иной форме, управлять технологическим процессом формования.

Заключение

• •    предложена реологическая модель формования тестовых заготовок с использованием

осесимметричного сдавливания постоянной силой сближающимися параллельными дисками;

• •    получены аналитические зависимости распределения давления и радиальной скорости течения моделируемой среды по поверхности сжимающих дисков;

• •    получены выражения для реологических коэффициентов µ и n , входящих в закон течения нелинейно-вязких жидкостей и показана возможность их экспериментального определения в опыте по осесимметричному прессованию;

• •    показано, что полученные в работе аналитические выражения позволяют управлять процессом осесимметричного прессования тестового материала.