Гидродинамическое сопротивление лесотранспортных единиц новой конструкции

На сегодняшний день актуальной проблемой лесного комплекса является транспортировка древесины от места заготовки. Лесные ресурсы, располагающиеся вблизи доступных транспортных путей, уже почти исчерпаны. В свою очередь, удалённые лесные массивы из-за отсутствия необходимой транспортной инфраструктуры не осваиваются.

Традиционно заготовленная древесина поставляется потребителю водным и сухопутным транспортом. Основу водного транспорта составляют судовые перевозки и зимняя береговая сплотка лесоматериалов с дальнейшим выводом их в плотах в весенний период. Для увеличения объёмов транспортировки лесоматериалов по внутренним водным путям необходимо совместно с зимней береговой сплоткой и судовыми перевозками восстановить навигационную сплотку древесины и разработать новые технологии сплава лесоматериалов, которые позволят вновь задействовать малые и средние реки. Для организации сплава по малым и средним рекам необходимы лесотранспортные единицы (ЛТЕ), обладающие малой осадкой, при этом имеющие высокие коэффициент полнодревесности и прочность. Также стоит отметить изменения, связанные с качественным составом лесных ресурсов. Доля лиственных пород постепенно увеличивается, что в перспективе должно привести к развитию технологий использования лиственной древесины.

Всем вышеперечисленным требованиям отвечает разработанная сплоточная единица (CЕ) [11], состоящая из четырёх пучков малого объёма (до 5 м³), соединённых между собой с помощью крепёжных брёвен 3 и гибких связей 4 , закреплённых фиксаторами 5 (рисунок 1).

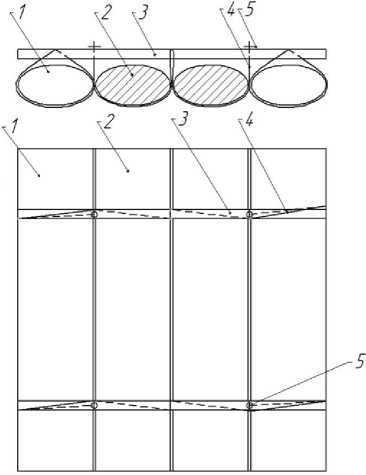
Рисунок 1. Сплоточная единица [рисунок авторов]

Figure 1. A float unit

Конструкция СЕ позволяет сплавлять лиственные сортименты. При этом пучки из лиственных сортиментов 2 устанавливают между пучками из хвойных сортиментов 1 . К достоинствам исследуемой нами СЕ можно отнести простоту формирования, высокую прочность и довольно большой объём при сравнительно малой осадке. Исследования гидродинамического сопротивления ЛТЕ, состоящих из предложенных СЕ, позволяют разработать научно обоснованные технические решения для лесосплава по малым и средним рекам.

Ранее вопросом организации сплава по рекам с малыми глубинами занимались А. А. Митрофанов [7], В. Я. Харитонов [14], Д. Н. Афоничев [2], А. Ю. Мануковский [6]. Изучению гидродинамических характеристик плоских сплоточных единиц, предназначенных для сплава по рекам с малыми глубинами, посвящены работы П. Н. Перфильева [13], О. В. Мурашовой [8]. В работах Д. Н. Афоничева [1], В. В. Васильева [11] приведены результаты исследований гидродинамических характеристик плотов, содержащих плоские сплоточные единицы стабилизированной плавучести. Особый интерес вызывают работы, связанные с изучением разгона, торможения и остановки ЛТЕ. Одним из первых неустановившееся движение ЛТЕ исследовал В. А. Щербаков [15]. Наиболее основательно данные вопросы отражены в трудах А. А. Митрофанова [8], М. М. Овчинникова [9], А. Ю. Мануковского [5], В. П. Корпачева [4], при развороте ЛТЕ — В. А. Барабанова [3].

Разработанная СЕ обладает конструктивными особенностями, отличающими её от других ЛТЕ, исследуемых ранее другими авторами. Таким образом, будут различными и гидродинамические характеристики. Эти отличия позволяют сделать вывод о целесообразности выполненных нами исследований.

2.    Материалы и методы

В статье представлены результаты исследования по неустановившемуся движению, в частности, по разгону ЛТЕ.

Эксперименты по изучению неустановившегося движения ЛТЕ проводились в опытном бассейне гравитационного типа [16]. Его ширина 3 м, длина 14 м, глубина 0,35 м. Размеры бассейна по ширине обеспечивали условия неограниченности потока. ЛТЕ состояли из 1…6 разработанных нами СЕ. Исследования проводились на моделях в масштабе 1 : 20 (фото 1). Моделирование неустановившегося движения ЛТЕ в этом масштабе считается надёжным, т. к. отсутствие масштабного эффекта было экспериментально подтверждено на моделях и в натурных условиях [7]. Рассматривался следующий диапазон размеров: высота СЕ Н = 0,05 м; отношение глубины наполнения бассейна к осадке h/Т = 7, 5, 4, 2.7, 1.6; отношение длины ЛТЕ к её ширине L/В 1…6. Коэффициент полнодревесности ЛТЕ η = 0,5.

При равномерном движении моделирование выполнено по критерию Фруда в интервале 0,16…0,48, а при неустановившемся — по критериям Фруда и гомохронности. Опыты проведены при числах Рейнольдса 3,1∙104…5,5∙105, где lл — длина линейки.

Фото 1. Модель исследуемой сплоточной единицы [фото авторов]

Photo 1. Model of the float unit

Модели буксировались при поперечном расположении модельных брёвен. Был задан диапазон скоростей равномерного движения ЛТЕ υ р 0,1…0,3 м/с, что соответствует натурным условиям — 0,45…1,2 м/с. Заданную скорость устанавливали в зависимости от массы буксируемого груза. Каждый эксперимент проводился не менее пяти раз для каждого значения скорости. В итоге было обработано 750 опытов.

Чтобы передать тяговое усилие, была использована трёхкратная полиспастная система. Эта система состояла из двух полиспастов: один передавал усилие тяги, а второй — усилие торможения. Блоки полиспастов выполнены из оргстекла и установлены на подшипниках. Диаметр каждого блока 100 мм, а толщина 4 мм.

В дальнейшем для сокращения записей эксперименты обозначаются кодом, состоящим из трёх цифр. Первая цифра указывает количество СЕ в ЛТЕ (1 — одна СЕ, 2 — две СЕ и т. д. до 6), вторая — серию экспериментов, т. е. при какой скорости, соответствующей натурной, буксировалась модель (1 — 1,2 м/с; 2 — 1,0 м/с; 3 — 0,8 м/с; 4 — 0,6 м/с; 5 — 0,45 м/с), третья — порядковый номер в серии. Отдельно указывается параметр h/Т.

В каждом опыте собирались данные о трёх режимах движения: разгоне, равномерном движении, торможении. Для анализа использовали только данные по разгону и равномерному движению модели. Движение моделей регистрировалось бесконтактным оптическим датчиком оборотов. Датчик создавал импульсы, частота повторения которых была пропорциональна частоте прохождения тахометрических меток, расположенных на вращающемся блоке со светоотражающим покрытием. Изменения частоты импульсов по времени фиксировались на компьютере c использованием программы ZetPanel. Для обработки полученных данных в программном обеспечении Microsoft Office Excel авторы создали макрос на языке Visual Basic for Applications.

Сила сопротивления воды равномерному движению ЛТЕ определяется по формуле

R = с ^ρ Ωυ² , 2^р

где с — безразмерный коэффициент сопротивления движению; ρ — плотность жидкости, кг/м3; Ω — характерная площадь (площадь миделя B × T), м2.

Для каждой модели получены зависимости вида R = aυ р ² (рисунок 2).

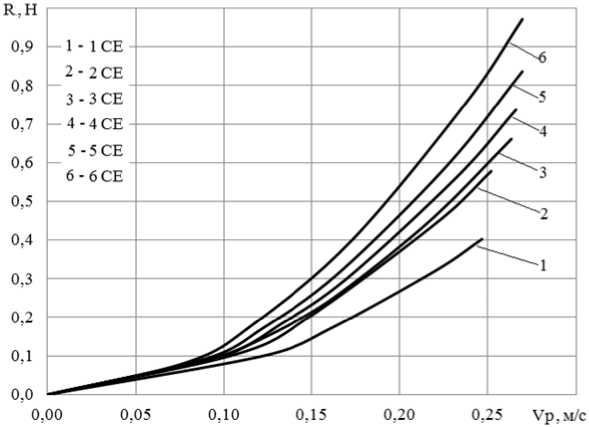
Рисунок 2. Графики зависимости сопротивления воды от скорости движения

моделей при h/T = 5 [рисунок авторов]

Figure 2. Graphs of the dependence of water resistance on the speed of models movement at h/T = 5

Значения параметра а представлены в таблице 1. Коэффициент детерминации 0,99.

Таблица 1. Значение параметра а , Н∙с²/м²

Table 1. Value of parameter а , N∙с²/m²

H/T	Д		ля ЛТЕ при L/B
	1	2	3	4	5	6
1,6	10,2	13,7	14,4	14,6	16,2	18,1
2,7	8,9	11,1	12,5	13,7	13,8	15,5
4	8,4	10,0	11,1	11,3	12,1	13,4
5	6,6	9,1	9,5	10,4	11,4	13,4
7	6,5	8,0	8,7	10,0	10,9	13,3

В общем случае главный вектор гидродинамических сил, действующих на объект при движении в вязкой несжимаемой жидкости, определяется как сумма трёх сил: силы плавучести Р п , инерционной гидродинамической силы Р ин и вязкостной гидродинамической силы Р ω :

Р = Р_п + Р_и н + Р . п ин ω .

Равнодействующая сил плавучести и веса ЛТЕ при отсутствии уклона свободной поверхности равна нулю.

Инерционная сила определяется по формуле

Р = Хм , ин м dt , где Хм — присоединённая масса; du/dt — ускорение движения тела, м/с2.

Проекция вязкостного компонента главного вектора гидродинамических сил на направление, противоположное поступательной скорости центра тяжести, даёт формулу для силы гидродинамического сопротивления ЛТЕ, определённую уравнением (1). Сила сопротивления при неустановившемся поступательном движении ЛТЕ представляет собой сумму двух сил:

R ' = R ± ARHe ст, нест где R — сопротивление воды равномерному движению ЛТЕ, вычисленное по гипотезе стационарности, Н; ΔRнест — дополнительное сопротивление, возникающее при неустановившемся движении, Н.

Масса ЛТЕ, определяющая её инерционные характеристики, состоит из суммарной массы древесины, коры и такелажа М Д и некоторой части воды М В , которая заполняет пространства внутри ЛТЕ.

В соответствии с теоремой об изменении количества движения тела, согласно которой производная по времени от количества движения тела равна главному вектору всех действующих на тело сил:

^{d (} M Д + М В + ^Хм } ^и dt          =^{- F +} P^,

где F — главный вектор внешних сил, Н.

Взаимозависимые переменные λ м , М В , и ΔR нест изменяются при различных режимах движения ЛТЕ. Их теоретическое или экспериментальное определение по отдельности невозможно. Коэффициент нестационарности движения n, объединяющий их, определяется следующим образом [8]:

dv

^Хм ⁺ М В ± ^ARнест

П =--------------

М Д

.

Эксперименты, проведённые различными авторами [7], [13], показали, что масса воды в ЛТЕ остаётся постоянной при её движении по поверхности воды. В этом случае сила буксировки моделей принимается за главный вектор внешних сил F. С учётом уравнения (3) уравнение (2) принимает следующий вид:

dυ

М д (i ⁺ n ) it =- R ⁺ f .

В результате было получено выражение для экспериментального определения значений коэффициента n:

n 2

F - а и

n =

- 1 .

dυ

М

Д dt

При известных значениях F, а и М Д для расчёта коэффициента n были определены мгновенные значения ускорения разгона ЛТЕ.

При обработке результатов опытов по разгону моделей были получены зависимости скорости и ускорения модели от времени вида:

-qt u = up - a Ue ;

dυ

= a ae -qt dt a где аυ, аа, q — параметры, определяемые экспериментально.

3.    Результаты

Пример результатов обработки разгона ЛТЕ серии опытов 23 при h/T = 5 приведён в виде графиков на рисунке 3. Коэффициенты детерминации для первой и второй зависимостей 0,99.

Полученные для всех моделей графики n = f (υ/υ р ) аппроксимированы линейными уравнениями вида:

υ

n = n1 + n 2 —, υр где n1, n2 — параметры эмпирической формулы.

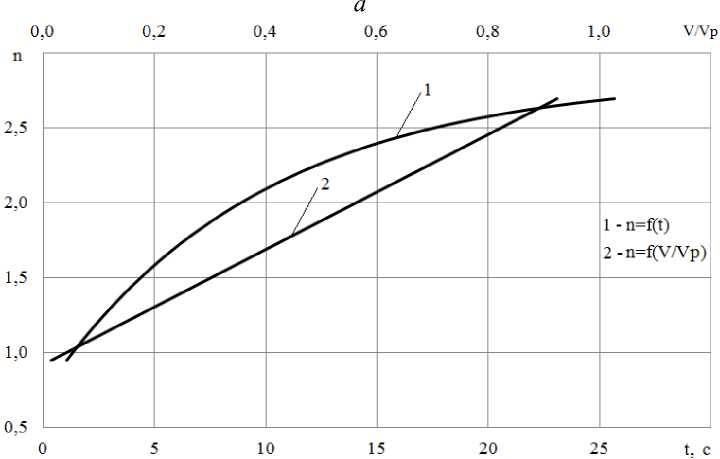
Коэффициенты n 1 и n 2 в уравнении (5) можно представить в виде функции от отношения L/B ЛТЕ (рисунок 4):

n 1 = f(L/B) , n 2 = f(L/B) .

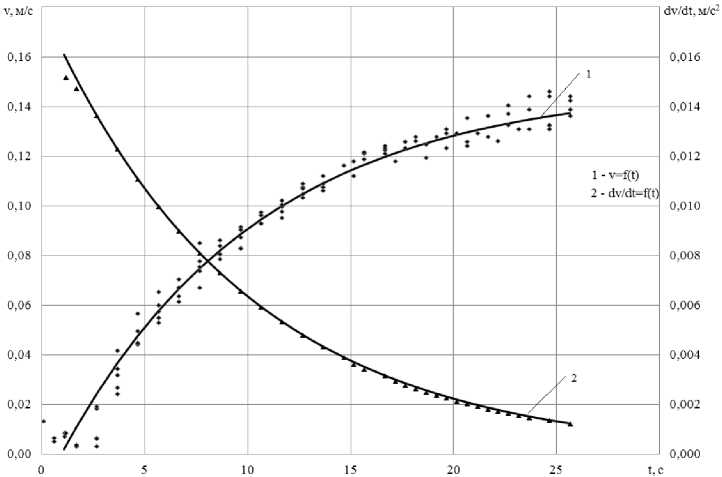
б

Рисунок 3. Результаты обработки серии опытов 23 по разгону модели при h/Т = 5: а — графики зависимости υ, dυ/dt от времени t; б — графики зависимости n от безразмерной скорости υ/υ р и от времени t [рисунок авторов]

Figure 3. Results of processing the series of experiments 23 on acceleration of the model at h/T = 5: (a) graphs of the dependence of υ, dυ/dt on time t; (b) graphs of the dependence of n on the dimensionless speed υ/υ р and on time t

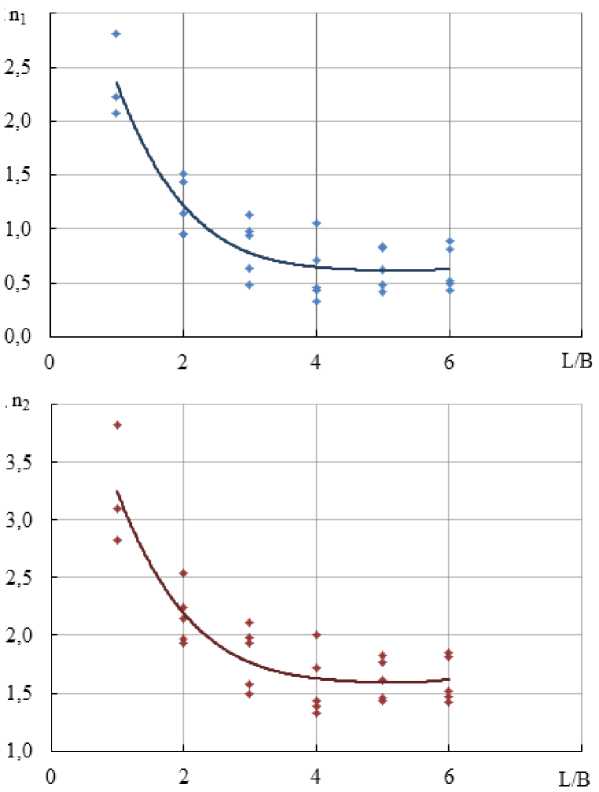
Рисунок 4. Графики зависимости n 1 = f (L/B); n 2 = f (L/B) при h/T = 1,6…7,0 [рисунок авторов]

Figure 4. Graphs of dependence n 1 = f (L/B); n 2 = f (L/B) при h/T = 1,6…7,0

Для каждой модели были определены значения коэффициентов n 1 и n 2 при отношении h/T в указанном диапазоне от 1,6 до 7,0, при котором влияние дна на гидродинамическое сопротивление отсутствует (таблица 2).

По результатам экспериментальных исследований обработано 134 серии опытов разгона ЛТЕ и получены расчётные формулы для определения коэффициентов n 1 и n 2 , справедливые для отношений h/T от 1,6 до 7:

n 1 = 0,01(L/B)⁴ - 0,19(L/B) 3 + 1,23(L/B)² - 3,70L/B + 5,02

n 2 = 0,01(L/B)⁴ - 0,17(L/B)³ + 1,12(L/B)² - 3,38L/B + 5,67

Коэффициенты детерминации при этом r² = 0,86 и r² = 0,81 для n 1 = f (L/B) и n 2 = f (L/B)

соответственно.

Таблица 2. Значения коэффициентов n 1 и n 2

Table 2. Values of coefficients n 1 и n 2

H/T	L/B	n 1	n 2	H/T	L/B	n 1	n 2
1,6	1	2,23	3,10	2,75	1	2,07	2,83
	2	1,14	2,15		2	1,44	2,24
	3	0,63	1,58		3	0,95	1,94
	4	0,45	1,39		4	1,05	2,01
	5	0,63	1,61		5	0,85	1,77
	6	0,53	1,52		6	0,89	1,85
4	1	2,816	3,83	5	1	—	—
	2	1,509	2,54		2	0,952	1,97
	3	1,136	2,11		3	0,4881	1,49
	4	0,717	1,72		4	0,4298	1,43
	5	0,831	1,83		5	0,4267	1,43
	6	0,814	1,82		6	0,4973	1,47
7	1	—	—
	2	0,96	1,94
	3	0,98	1,98
	4	0,33	1,33
	5	0,49	1,46
	6	0,43	1,42

Задаваясь размерами ЛТЕ и используя формулы (5) и (6), можно определить коэффициент n для любой величины безразмерной скорости υ/υ р .

Результаты экспериментальных исследований по определению n 1 и n 2 на «глубокой» воде (h/T = 7) сопоставимы с результатами, полученными А. А. Митрофановым [7].

4.    Обсуждение и заключение

Надёжная транспортировка ЛТЕ возможна при условии их управляемости. Это особенно важно в речных условиях при расхождении со встречными судами, на поворотах и участках с поперечным течением. Управляемость ЛТЕ достигается при скорости буксировки относительно потока от 0,4 до 0,9 м/с. При проведении технологических расчётов переместительных операций с ЛТЕ необходимо знать время и путь разгона ЛТЕ до скорости, при которой обеспечивается их управляемость.

Полученные результаты и решения уравнения (4) позволяют определить время и расстояние, которое требуется для разгона лесотранспортных средств. Также можно решить другие задачи, например, вычислить необходимую силу разгона для достижения определённой скорости движения ЛТЕ, близкой к равномерной, за конкретный период времени.