Гидродинамическое взаимодействие двух всплывающих капель

В классическом методе отслеживания фронтов (FTM) [1], [2] движение двухфазной несжимаемой среды описывается единой системой уравнений Навье — Стокса du + (u • V)u = - ^—Vp + f + V • ©Vu + VTu) + У ак'п'5(х — x0) ds0^ ,

V • u = 0, где u, p — скорость и давление, ρ, µ — плотность и вязкость жидкости, f — объемные силы, κ0 — кривизна межфазной поверхности, σ — коэффициент поверхностного натяжения. При этом на границах частиц плотность и вязкость терпят разрыв. А силы межфазного взаимодействия, действующие на границе частиц, учитываются в (1) последним интегралом, в котором интегрирование ведется по поверхностям всех дисперсных включений.

Кроме неподвижной прямоугольной сетки для расчета полей скорости и давления, на границе каждой дисперсной частицы также задается одномерная криволинейная подвижная сетка, которую называют фронтом, при помощи которой отслеживается перемещение и деформация частиц. В течениях с интенсивным слиянием и разрушением частиц перестройка границ для классического FTM представляет большие алгоритмические трудности, в связи с этим возникает потребность в изменении методов отслеживания для применения в исследованиях таких течении. Один из таких методов был предложен в [3].

В настоящей работе методом отслеживания границ была решена задача о гидродинамическом взаимодействии двух деформируемых капель, всплывающих в покоящейся жидкости. За основу для численного решения уравнений (1), (2) взят метод, подробно описанный в [4], [5].

• 1.    Отслеживание деформирующихся и разрывающихся границ

• 2.    Взаимодействие пары капель

Идея метода построения фронтов, примененного в настоящей работе, состоит в том, что для задания положения границ используется линия уровня, соответствующая некоторому значению скалярной функции-индикатора I f , удовлетворяющей уравнению

V I f = J 5 (x — X f ) ds.

Процесс перестройки фронтов состоит из двух этапов. Cначала, используя текущее положение фронта, восстанавливается функция I f , далее строится новый фронт. Это делается путем проведения линии уровня, соответствующей значению I f = 0 , 5 . При таком построении элементы из соседних ячеек будут иметь одинаковое расположение конечных точек, а поскольку для точек с одинаковыми координатами скорость одинакова, то и перемещаться они будут одинаково. В данном методе близкие границы автоматически объединяются, как только они сблизятся на расстояние нескольких ячеек. Частота обновления фронтов зависит от конкретной задачи и не требует перестройки на каждом шаге по времени.

В работе [6] методом отслеживания фронтов проводились расчеты движения небольшого облака частиц в параболическом потоке, при этом допускалось лишь сближение отдельных частиц, но их объединения не происходило, а значительные деформации капель не приводили к их распаду. В настоящем же исследовании численно моделировалось движение двух одинаковых цилиндрических жидких капель в другой покоящейся жидкости.

Целью было не оценить общие пульсационные гидродинамические поля, а адекватно описать динамику парного взаимодействия капель и эволюцию их границ, которые могут деформироваться, сливаться и распадаться. Соотношения параметров дисперсионной и дисперсной фаз брались следующие: р ₀ /р 1 = 20 , ^ 0 /^ 1 = 20 , где индекс «0» обозначает несущую жидкость, а «1» — капли другой жидкости. Характерные безразмерные параметры локального течения (числа Рейнольдса, Фру-да, Вебера), рассчитанные по радиусу частицы, в численных экспериментах задавались соответственно Re = 100 , Fr = 0 , 25 , We = 2 . Расчеты проводились на сетке 384 х 256 , которая покрывала область [0; 1] х [0; 1 , 5] , а по времени они продолжались до момента достижения облаком границ расчетной области.

Рис. 1. Вертикальное расположение капель

Вертикальное расположение капель. В первом случае капли всплывали соосно друг за другом (рис. 1). Верхняя капля приобретала сплющенную форму, нижняя вытягивалась и впоследствии, увлекаемая потоком от головной капли, сливалась с первой. Затем происходило разделение капли по вертикальной оси симметрии на две половинки. Края этих половинок, расположенные ближе к центральной оси, заворачивались внутрь. С противоположного края потоком срывались фрагменты малого размера (r ~ 0 , 1 R) и, находясь в следе от основных капель, они участвовали в вихревом движении несущей жидкости. Далее крупные капли двигались рядом друг с другом, совершая вращательные покачивания.

Горизонтальное расположение капель. Во втором численном эксперименте рассматривалось начальное расположение капель на одном горизонтальном уровне (рис. 2). В начале движения края, расположенные рядом друг с другом, вытягивались нисходящим потоком в хвосты. По достижении критической длины перемычки, соединяющей основную каплю и снесенную часть, происходил ее разрыв. Аналогичный процесс имеет место с противоположного края частиц, но на этот раз наряду с отрывом происходит образование двух вихрей, которые остаются неподвижными немного выше изначального расположения капель. Далее капли всплывали, теряя фрагменты то с внутреннего края, то с внешнего, совершая при этом покачивания, затухающие со временем из-за увеличения расстояния между каплями.

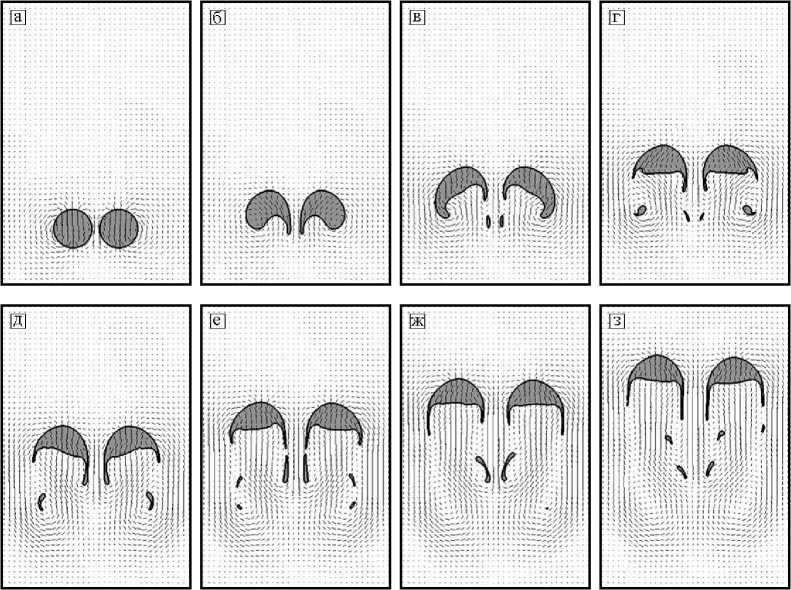
Рис. 2. Парное всплытие

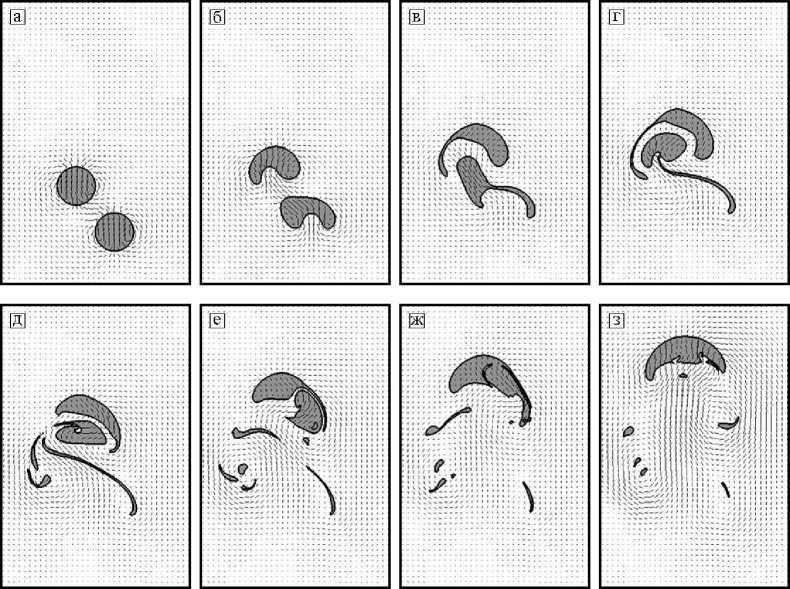
Рис. 3. Несимметричное всплытие капель

Несимметричное всплытие капель. В последнем эксперименте рассматривалось всплытие капель, которые в начальный момент располагались несоосно как по вертикали, так и по горизонтали (рис. 3). Отстающая капля отклонялась от прямолинейного движения, увлекаемая следом опережающей частицы, но они не сразу объединялись как в первой задаче. Головная капля двигалась вправо и вверх, а отстающая продолжала следовать за ней. Совершив такое зигзагообразное движение, капли догоняли друг друга, объединялись в одну и далее двигались как единое целое.

Заключение

Методом отслеживания фронта было проведено численное моделирование гидродинамического взаимодействия двух деформируемых капель при их поступательном всплытии. Проведено три численных эксперимента в полной постановке для различного начального расположения капель. В процессе всплытия капли испытывали значительные деформации и дробились, и при этом алгоритм построения межфазной границы работал вполне адекватно. Так, изменение суммарного объема капель в первом и втором эксперименте не превышало 5 %. В случае несимметричного всплытия капель при значительном измельчении хвостовой части границы некоторых фронтов не разрешались, и потери полного объема составляли более 20 %. Однако в данном случае, при наличии больших деформаций, слабым местом является не сам алгоритм перестройки границы, а недостаточная мелкость неподвижной сетки.