Гидродинамика и теплообмен при вынужденной конвекции некоторых микробиологических сред

Приводятся обобщённые результаты экспериментального исследования конвективного теплообмена при вынужденном течении в вертикальных трубах и плоско-параллельных каналах ряда характерных для биотехнологии рабочих сред: культуральных жидкостей, нейтрализатов, гидролизатов, полиглюкинов, после дрожжжевого остатка (ПДО) и др. Обсуждаются причины обнаруженных особенностей гидродинамики и теплообмена указанных сред в ламинарной, переходной и турбулентной областях течения. Ставятся задачи дальнейших исследований.

Развитие теплофизики постоянно связано с решением прикладных задач инновационных технологий. Решая на основе фундаментальных исследований практические задачи создания теоретических основ инженерных методов расчета, теплофизика постоянно обогащается за счёт изучения новых сред, теплоносителей, расширения диапазонов режимных параметров и др. В последние десятилетия в мире ускоренными темпами развивается биотехнология, которую отличают значительная доля теплоиспользующего оборудования и энергоёмкость производства. Поэтому промышленное освоение процессов биосинтеза ввело в круг актуальных для теплофизики прикладных задач изучение теплообмена в биологических и микробиологических средах [1].

Микробиологическая технология базируется на закономерностях, свойственных популяциям микроорганизмов, получаемых как в промышленных условиях, так и существующих реальных живых организмах. При этом биологическая форма движения материи с присущим ей многообразием определила ряд специфических особенностей микробиологических сред (биомассы, культуральной жидкости, продуктов метаболизма клеток и др.). 65

Сюда относятся: вариабельность и многокомпонентность, низкие концентрации и скорости реакций, переменность в ходе процесса реологических свойств, проявление у белков одновременно свойств аморфных электролитов и коллоидных растворов и многое другое [2].

Для создания методов расчёта и оптимизации параметров технологического оборудования требуются достоверные сведения о процессах теплообмена, необходимы такие данные и для расчётов биофизических процессов внутри организмов. Построение достаточно обоснованных физических моделей соответствующих процессов невозможно без определённого набора первичной экспериментальной информации, которая позволила бы определить место рассматриваемых сред в теплофизике. Одновременно такая информация открывает возможности выполнения необходимых инженерных расчётов. То обстоятельство, что практически все микробиологические среды являются слабо концентрированными водными растворами, даёт основания предположить сходный характер процессов конвективного теплообмена с однокомпонентными средами и искать решение в данном направлении.

Ниже приводятся некоторые результаты обобщения данных экспериментальных исследований теплообмена при вынужденной конвекции ряда микробиологических сред. Опыты проводились на вертикальном плоско-параллельном канале и трубах, имеющих эквивалентный диаметр 12…32 мм, длину 1000…6000 мм и снабжённых предвключённым участком гидродинамической стабилизации. Предварительные опыты по определению потерь давления по длине канала и тенеграммы течения жидкости, полученные на плоско-параллельном канале, подтвердили, что протяженность участка гидравлической стабилизации l _т при Pr>1 была короче, чем протяжённость области тепловой стабилизации l _г, что согласуется с данными многочисленных исследований. Тепловой поток создавался с помощью электрического тока. В опытах на трубе диаметром 32 мм и длинной 6000 мм тепловой поток создавался с помощью парового обогрева. Максимальная скорость исследуемых жидкостей в каналах составляла 3,5 м/с. Тестирование экспериментальных установок производилось с помощью опытов на воде, которые дали хорошую сходимость с известными зависимостями.

Исследовались следующие культуральные жидкости: дрожжевая суспензия и суспензия БВК в диапазоне концентраций

С =2,5…20%; отработанная культуральная жидкость (ПДБ) в диапазоне С =1…15%; остальные среды при фиксированных значениях концентрации, соответствующих технологическим условиям. Кроме того, были исследованы водные растворы полиглюкина (заменителя крови) при С =0,1..10% и глюкозы при С =2…25%. Влияние окислительно-восстановительной среды на теплообмен определялись для диапазона pH =1…4,5. Тепловая нагрузка в опытах варьировалась в диапазоне q=50…200 кВт/м², массовая скорость ρW=100…2500 кг/(м²·с), температура жидкости t_ж=20…95⁰С, давление оставалось близким к атмосферному. Закономерности теплообмена теплообмена изучались для условий стабилизированного течения в турбулентной и переходной областях течения. Для ряда жидкостей были рассмотрены также особенности теплообмена в ламинарной области течения.

Основные результаты проведенного исследования сводятся к следующему:

Ламинарный режим течения. За основу, при обобщении экспериментальных данных по теплоотдаче на участки тепловой стабилизации при ламинарном течении и вязкостном режиме теплообмена (Gr·Pr<250), было принято известное интерполяционное уравнение, которое для плоского канала и условий q _x=const, принимает вид

Nu « 1,3 -(Pe • d 11 )I3 -Ц I ц У, (1)

и, как известно, с точностью ±4% описывает точное решение. Показатель степени m при симплексе μ / μ _w, учитывающем влияние теплообмен переменной вязкости, для случая подъёмного движения жидкости соответствует величине m ≈0,14. Принятый подход позволил обобщить экспериментальные данные с точностью до коэффициента, при этом была подтверждена степенная зависимость

Nu ~ ( Pe • d 11 ) ^I3 . (2)

Обобщение опытных данных по дрожжевым суспензиям позволило получить значении коэффициента пропорциональности в формуле (1) равное 2,3, для гидролизатов получено несколько иное значение, а именно 2,1. Погрешность аппроксимации в данном случае лежит в пределах +50%. Естественно было предположить, что столь существенное расхождение связано с проявлением реологических свойств рассматриваемых сред. В обзоре Е.М.Хабахпашевой [3] отмечается, что для учёта изменения вязкости неньютоновских жидкостей, обусловленного наличием радиальных температурных градиентов, обычно пользуются приближёнными методами, представляющими собой обобщения известных степенных поправок; в общем случае течения структкно-вязких жидкостей следует учитывать влияние на теплообмен не только соотношения вязкостей, но и величины l/(Pe·d).

Основываясь на указанных положениях, мы стремились добиться удовлетворительного обобщения экспериментальных данных, ограничиваясь только уточнением степенной поправки, поскольку для исследуемых сред с помощью принятых методов измерения определить градиенты скорости у стенки не удавалось. Соответственно не мог быть вычислен коэффициент χ, учитывающий структурно-вязкие свойства. Поэтому в качестве параметра был сохранён симплекс ^ / Pw ^ . На его основе в результате обобщения опытных данных получена уточнённая зависимость

Nu «1,3 -(Pe • d 11)/3 -(и / ^w )P,25, (3)

аппроксимирующая опытные данные с погрешностью ±12%. При этом коэффициент теплоотдачи для дрожжевых суспензий получен примерно на 15% выше, чем для ньютоновских сред при тех же значениях μ / μ _ж. Сопоставление наших результатов с данными, приведенными в обзоре [3], позволяет предположить, что рассматриваемые среды следует отнести к жидкостям с линейным или квадратичным законом текучести. Окончательный ответ на данный вопрос можно получить только в результате детального изучения реологических свойств микробиологических сред, что должно стать предметом дальнейшего достаточно углублённого исследования.

Переходный режим течения. Вопросы теплоотдачи в переходной области течения для жидкостей, проявляющих неньютоновские свойства, до настоящего времени изучены мало. Отмечается [3], что наличие структурной вязкости ведёт к затягиванию перехода к турбулентному режиму течения. Наши экспериментальные данные также указывают на некоторое затягивание перехода, при этом был отмечен ряд закономерностей.

При фиксированном значении чисел Прандтля теплоотдача ( Nu ) характеризуется серией кривых, имеющих общую область пропорциональности числу ( Re ^1,34). С погрешностью ±10% можно утверждать, что коэффициент пропорциональности является функцией числа Pr и аппроксимируется соотношением

Nu

_Re 1,34

= 1,64 - 10 - ⁴ ■ Pr ¹'¹ .

Поскольку для обобщения был приняты только данные, соответствующие вязкостному и вязко-инерционному режимам течения, диапазон изменения μ / μ _ж в опытах был невелик, поэтому данные удалось обобщить, не вводя параметр ( μ / μ _ж)^0,25. Однако в общем случае, он, очевидно должен быть введён в формулу (4).

Таким образом, формула для расчёта интенсивности теплоотдачи в трубах и каналах для переходной области течения культуральных жидкостей была получена в виде

Nu пер = 1,64 ■ 10 ⁴ Pr ¹'¹ Re ¹'³⁴ .        (5)

Максимальное отклонение экспериментальных данных от зависимости (5) не превышает ±15%, что для переходной области, которая характеризуется вообще нестабильностью течения и пульсациями параметров можно признать удовлетворительной точностью. Анализ результатов опытов показал также, что области, описываемой формулой (5), предшествует некоторая область неустойчивого теплообмена, где значения Nu выше Nu _∞, определённого для ламинарной области. При этом было установлено, что для плазмолизованных дрожжевых суспензий при Pr= 7…120 минимальное значение чисел Nu и Re, соответствующее началу выше указанной устойчивой переходной области течения, подчиняется соответственно зависимостям

Nu Нер = 4,9 ■ Pr⁰⁵ ;             (6)

Re нер = 2 ■ 103 ■ Pr-06.         (7)

Интересно отметить, что при Pr=0,72 (воздух), формула (6) даёт хорошо известное теоретическое решение Nu _∞≈4,36, а формула (7) – также хорошо опробованное значение Re_к р ≈2300.

Отмеченная выше зависимость потери устойчивости от числа Прандтля согласуется с данными А.А.Жукаускаса и А.А.Шлянчаускаса [4], которые справедливо отмечают, что такой характер зависимостей можно объяснить тем, что при больших значениях числа Прандтля тепловой пограничный слой значительно утоняется по сравнению с динамическим. В результате имеющие место в пристенной области малые возмущения начинают играть относительно большую роль в процессе перехода и ускоряют его начало.

Турбулентный режим течения . Как уже отмечалось выше, основная часть наших исследований относилась к турбулентной области течения, как наиболее типичной для технологического оборудования. Опытные данные по теплоотдаче при турбулентном течении капельных жидкостей (и газов) в трубах и каналах, как известно, хорошо аппроксимируются соотношением

Nu = A Re ⁰’⁸

Pr ⁿ

0,25

Pr

Pr

V Pr w 7

.

При этом известно, что в зависимости от направления теплового потока, значения числа Pr, условий эксперимента и т.п. получаемые в экспериментах значения А и n в этой формуле колеблются в пределах: А = 0,021…0,026; n=0,3…0,6. Тестовые опыты, проведенные нами на воде, с погрешностью ±10% подтвердили ставшие классическими значения: А =0,023; n =0,4. Поэтому при обработке и анализе результатов последующих опытов на других жидкостях искалась зависимость вида

Nu = К • 0.023Re ⁰’⁸ Pr ⁰’⁴

0,25

Pr

Pr

V Pr w 7

,

где К – коэффициент, учитывающий индивидуальные свойства жидкости.

Резюмируя результаты проведенных исследований, отметим, что они подтвердили возможность в целом ряде случаев пользоваться указанным подходом, однако не для всех исследованных жидкостей.

Так для культуральных жидкостей типа ПДБ с погрешностью ±15% опытные данные обобщаются с помощью зависимости (9) при К =1. Для дрожжевых суспензий с аналогичной погрешностью получено значение К =1,216. В ряде работ указывается [3], что расчёты коэффициентов теплообмена для нелинейно-вязких жидкостей можно осуществлять по формулам для ньютоновских жидкостей, если вычислять значения чисел Re и Pr по величине вязкости на стенке. Такая обработка была произведена нами для дрожжевых суспензий. Погрешность аппроксимации при этом увеличилась до ±25%, поэтому в дальнейшем от подобной обработки пришлось отказаться.

Самостоятельную группу составили гидролизаны и нейтрализаты , их теплоотдача подчиняется одинаковым закономерностям, причём эти закономерности отличаются от общеизвестных. В частности, теплоотдача указанных сред в турбулентной области течения оказалась пропорциональной Re^0,47, что исключало возможность применения для обобщения зависимости (9). Кроме того, была установлена некоторая зависимость теплоотдачи от pH (диапазон изменения pH =1…4,5). Иная зависимость теплоотдачи от числа Re определила то обстоятельство, что для данных сред существует область (Re≈7·10³…3·10⁴), где теплоотдача выше, чем для воды, и область (Re>3,5·10⁴), в которой теплоотдача ниже, чем для воды (см. рис.1). Отсюда становятся объяснимыми противоречивые данные относительно соотношения теплоотдачи воды и гидролизатов, встречающиеся в ряде нормативных документов.

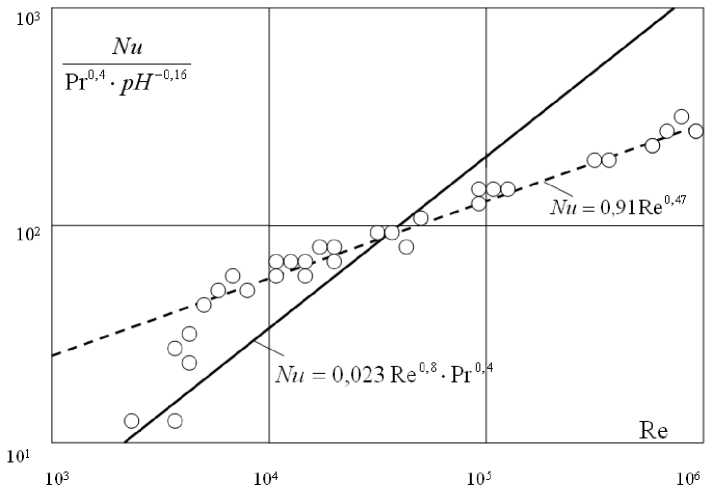
Рис. 1. Сопоставление теплоотдачи воды и гидролизатов в турбулентной области течения.

Визуальные исследования показали, что для гидролизатов и нейтрализатов при переходе к турбулентному режиму течения характерно помутнение – они перестают быть прозрачными. Нами высказано предположение, что данное обстоятельство связано с образованием пенно-эмульсионной структуры. В этом случае теплоотдача действительно может несколько увеличиваться, благодаря интенсификации массообменных процессов в момент образования пены. То обстоятельство, что при дальнейшем увеличением числа Re темп увеличения теплоотдачи примерно такой же, как в ламинарной области течения, позволяет предположить, что пенно-эмульсионная структура при общей интенсификации теплообмена обусловливает условия течения в пристенной области близкие к ламинарному.

Здесь необходимо отметить, что параметр pH определяет молекулярное взаимодействие на границе раздела фаз растворов, содержащих поверхностно-активные вещества, и тем самым характеризует устойчивость пенных структур. В такой постановке становится понятным влияние pH на теплообмен. Однако отмеченные особенности могут быть связаны также и с изменением физических свойств жидкостей и структурной вязкостью эмульсий, влияние pH при этом будет носить косвенный характер.

Окончательный ответ может быть получен только на основе детальных исследований локальных характеристик потока и структуры течения. Поэтому на данном этапе мы вынуждены ограничиться обобщением результатов опытов формулой

Nu = 0.91Re °’⁴⁷ ( pH ) 6 ,         (10)

которая аппроксимирует опытные данные с погрешностью не превышающей ±20% в области 7·10³< Re <10⁶, 1< pH <4,5.

Полиглюкины составили отдельную группу среди исследованных сред, для них обнаружена аномалия теплоотдачи в области малых концентраций и затягивание перехода к развитому турбулентному течению. Последнее обстоятельство, по-видимому, связано с влиянием полимерных свойств жидкости. Из ряда работ, например, [5], известно, что эффект Томса проявляется в жидкостях с малыми полимерными добавками обычно при турбулентном течении.

Интенсивность теплообмена для водных растворов полиглюкина (при одинаковых числах Re) ниже, чем для воды. На рис. 2 представлена экспериментально полученная зависимость изменения коэффициента К (см. формулу (9)), от процентной весовой концентрации абсолютно сухих веществ (а.с.в.). Как видно из приведенного графика в области малых концентраций С =0,1…0,5% наблюдается резкое снижение теплоотдачи. С увеличением концентрации до С ≈1% теплоотдача несколько возрастает, далее опять снижается, стабилизируясь при С ≈3%.

Приведенные данные позволяют отнести слабые водные растворы полиглюкина к жидкостям с высокополимерными добавками, где, как известно, было обнаружено существование оптимальных малых концентраций, при которых снижается сопротивление [3]. Опыты Е.М.Хабахпашевой и Б.В.Перепелицы [6] показали, что основное действие полимерных добавок проявляется в снижении интенсивности поперечных компонент пульсации скорости. Поскольку указанные пульсации вместе с пульсациями температуры определяют интенсивность теплообмена между потоком и стенкой, естественно ожидать уменьшения теплоотдачи.

Для сравнения были проведены опыты с водными растворами глюкозы и глицерина, которые носили, в известной степени, методический характер. Отмечено, что, так же как и у 73

полиглюкина, интенсивность теплоотдачи для указанных растворов с увеличением концентрации снижается, но не столь интенсивно.

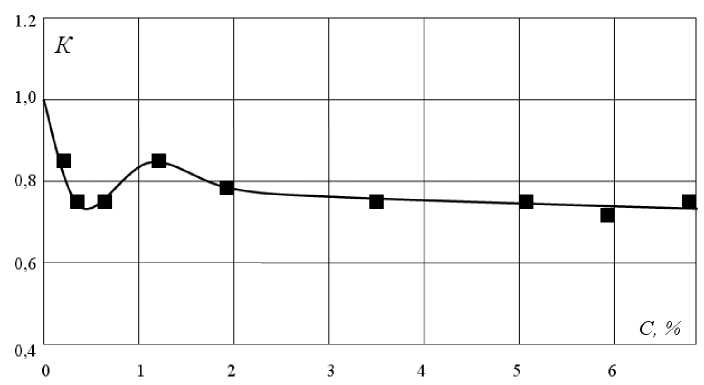
Рис. 2. Зависимость коэффициента К в формуле (9) от концентрации а.с.в. для полиглюкина.

Из-за отсутствия достаточного объёма данных о теплофизических свойствах для полиглюкина и ему подобных сред при вычислении критериев подобия использовались значения физических констант для воды. Поэтому наряду с критериальной была произведена обработка опытных данных в размерном виде, что позволило получить зависимость а = exp(- B • C), (11) α0

где α 0 – теплоотдача для дистиллированной воды; В – коэффициент, зависящий от рода жидкости; С – весовая концентрация абсолютно сухих веществ (а.с.в.), в процентах. Для водных растворов полиглюкина в области С =1,3…10% - В =3,35; для водных растворов глюкозы при С =2…25% - В =0,97; для водных растворов глицерина при С =5…40% - В =1,22.

Изложенные выше результаты исследования теплообмена микробиологических сред позволили выявить ряд специфических особенностей, отличающих указанные среды от однокомпонентных жидкостей. В ламинарной области течения эти особенности проявляются незначительно и сводятся к увеличению области тепловой стабилизации на входном участке канала и затягиванию начала переходной области течения. Переходная область носит более размытый характер и заканчивается при больших значениях критерия Re. Наибольшие отличия наблюдались в области турбулентного течения. Здесь для ряда микробиологических сред отмечена аномалия теплоотдачи в области малых концентраций, слабая зависимость теплоотдачи от числа Re, переход к турбулентному режиму при больших значениях Re и др. Ряд отмеченных особенностей находит объяснение на основе современных представлений о реологических средах, а также представлений о влиянии окислительно-восстановительного потенциала на пенообразования жидкостей; некоторые особенности пока ждут своего объяснения.